可充电概率传感网络中的充电小车休息时间最大化方法

冉现源，王 然

(杭州电子科技大学 计算机学院，浙江 杭州 310018)

无线传感器网络已被应用于环境监测、灾害预警、智慧城市等多个行业中[1-2]。由于网络中每个传感器通过有限容量的电池进行供电，因此延长传感器的寿命是一个关键问题[3]。针对该问题的现有解决方案包括节能[4]、电池替换[5]、能量收集等[6]。然而节能并不能弥补网络的能量损耗；更换电池成本高昂，不切实际；能量收集的方式对环境变化较为敏感，无法为传感器提供稳定及时的能量供应。

近年来，无线能量传输(Wireless Power Transfer，WPT)技术的发展为传感器网络能量补充提供了新的思路。文献[7]通过物理实验提出了全向磁共振耦合充电技术。该技术不需要移动充电小车(Mobile Charger，MC)与传感器直接接触就能实现稳定高效的能量传输。文献[8]提出一种多节点能量充电方案，通过适当调节发送线圈和接收线圈的工作频率，可同时对多个传感器充电，从而提高能量转移效率，扩大能量传输范围。基于WPT技术，优化调度移动充电小车充电已成为研究热点[3，9-11]。

现有的多节点充电研究[9，12-14]中，部分研究人员为了保证网络永久运行，移动充电小车在一次循环中需要尽可能地响应网络中所有节点的请求。该方法大幅增加了运行成本，在大型网络中难以实现。MC相对传感器成本更加昂贵，因此优化调度单MC在最短时间内完成充电任务来最大化其充电循环中的休息时间[15]就显得尤为重要。实际网络环境中，低成本的传感器通常被高密度地冗余部署[16]。利用这种冗余性，允许部分节点耗尽能量，但仍保持网络永久监测功能，通过放宽“所有节点不可死亡”这种要求的严格性来降低MC运行成本。为了保证这种策略的监测质量，本文要求网络中的每个目标时刻保证ε覆盖[17]。在安全监控应用中，ε覆盖可以更高质量地识别物体。

本文在无线可充电概率传感网络(Wireless Rechargeable Probabilistic Sensor Network，WRPSN) 中使用ε覆盖来提供高质量的目标监测，并使用多节点充电模型来利用冗余节点，提高充电效率，降低MC运行成本，将MC的休假时间比例最大化。

1 模型与问题描述

1.1 概率监测模型

本文采用指数衰减概率监测模型[18-19]，节点si对目标点oj的监测概率pi，j可以表示为如下形式

(1)

式中，β和λ表示传感器物理特性的参数；d(si，oj)表示传感器si到目标点oj的欧式距离；rmax表示传感器的最大有效监测半径。

定义1联合监测概率。对于任意目标，它的监测概率要求不小于ε，那么对于被传感器集合Sj所监测到的目标oj来说，联合监测概率P(oj)满足式(2)中的关系

P(oj)=1-∏i∈Sj(1-pi，j)≥ε

(2)

对式(2)进行移项可得

1-ε≥∏i∈Sj(1-pi，j)

(3)

对式(3)进行对数变换可得

(4)

对式(4)进行变换可得

(5)

式(5)定义φi，j=-ln(1-pi，j)为节点si对oj的监测增益，Ψ=-ln(1-ε)为每个目标点所需满足的监测增益阈值。

定义2混合增益为对于网络中的任一目标o，当开启其周围距离小于rmax的部分传感器时，得到的增益总和。

定义3过剩增益。对于给定目标o和其周围激活的一组传感器，当传感器协同工作时，使目标o的混合增益超出增益阈值Ψ的部分称为过剩增益。

1.2 能量传输模型

本文采用多节点全向无线充电模型，MC充电范围是一个以D为半径的圆形区域，只有传感器节点和MC的距离小于D时，才能进行有效充电。

假设传感器节点si的能量接收功率为Pin(si)，MC在充电时的能量传输功率为Pout，移动能耗率为Pmov，Di是节点和MC间的欧式距离。μ(Di)是MC与传感器之间的能量传输效率，传输效率随着两者之间距离的增大而衰减，其取值范围为(0，1]。可以通过式(6)计算节点si的接收功率值。

(6)

1.3 网络模型

本文考虑的WRPSN包含：(1)N个同质的可充电概率传感器节点；(2)M个同质的待监测目标点；(3)1个具有多节点充电功能的MC；(4)1个基站(Base Station，BS)；(5)1个供MC休息的车站(depot)。如图1所示，传感器节点和目标点随机部署在二维平面内的1个方形区域内，每个节点的初始电池容量相同，MC可以对多个节点同时充电，MC电池容量为Emc，恒定移动速率为v。本文假定BS位于区域中心，用于收集监测数据，MC在depot补充电量，每次充电循环的起始点都是depot。

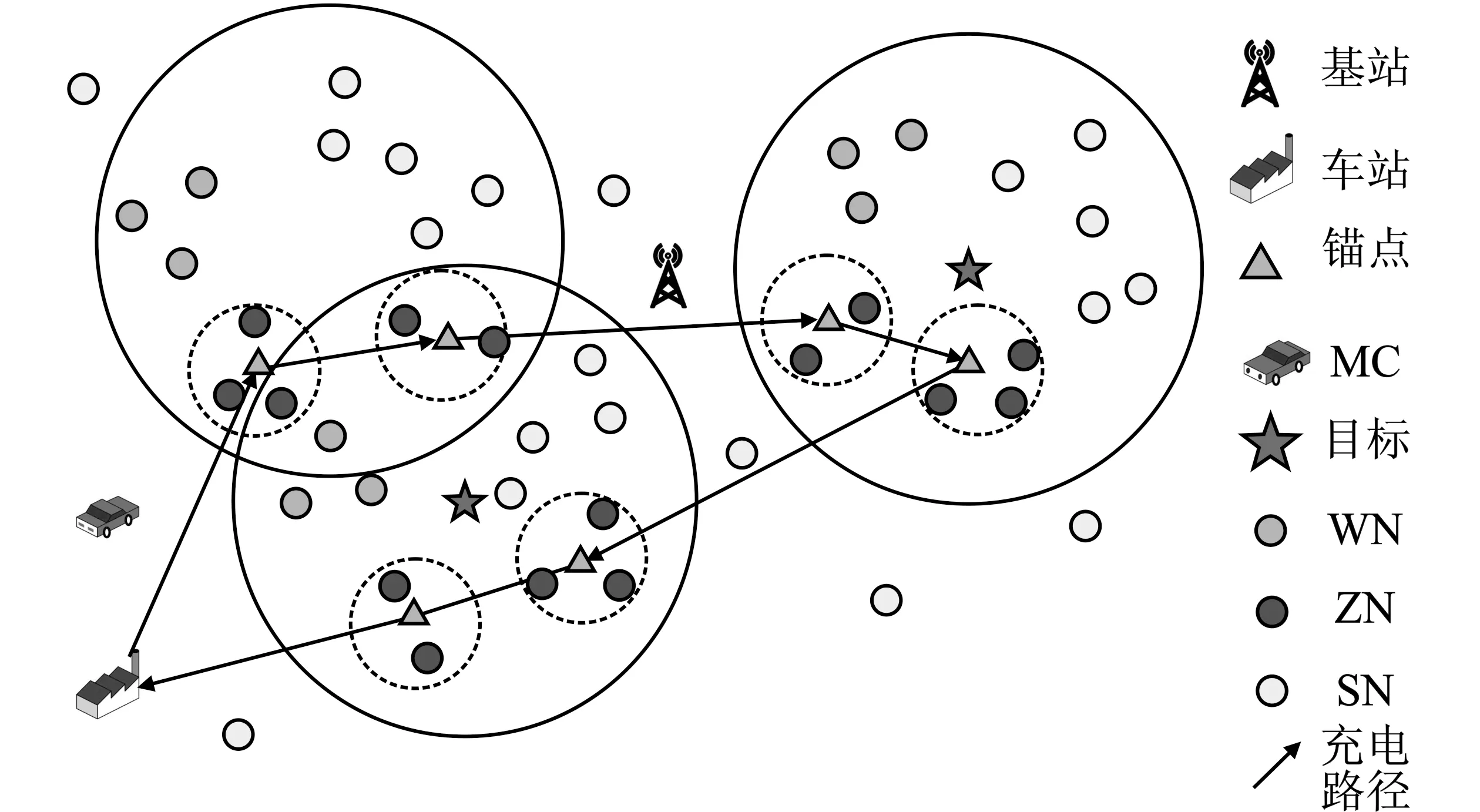
图1 无线可充电概率传感器网络Figure 1. Wireless rechargeable probabilistic sensor network

当目标周围可工作子簇个数低于阈值η时，就会发出充电请求。本文将网络中的节点分为3类：工作节点(Working Node，WN)、零能量节点(Zero Energy Node，ZN)和休眠节点(Sleep Node， SN)，工作节点的能耗固定为es，休眠节点的能耗可以忽略。

2 问题定义

给定的平面区域内包含待监测的目标集合O={o1，…，oM}和大量随机均匀抛洒的节点集合S={s1，…，sN}。为了有效利用目标点周围大量的冗余传感器来均衡目标周围的可用增益，将目标周围的传感器划分为簇。目标oj的簇记为Cj，每一轮从目标簇C1，…，CM中选择传感器子簇激活，完成ε概率覆盖要求。当选中的这部分传感器耗尽能量后，激活下一组传感器。当目标点周围剩余可用子簇的个数低于阈值η时，发出充电请求，MC选择锚点来对部分节点充电，以保证网络持久运行，最终实现恒定充电周期中MC休息时间比例最大化。

假设A0表示depot的位置，使用有序集合AP={A0，A1，…，Am，A0}来表示其中1个充电周期内的充电路径，其中m是锚点的个数，充电路径长度为Lmc，移动时间为Lmc/v。MC对其充电覆盖范围内的每个节点都充满电所需的时间取决于接收功率最小的节点的充电时间，因此MC在锚点Aj处的充电时间tc(Aj)表示为

(7)

式中，ωj表示在锚点Aj可以被同时充电的传感器集合；ti(Aj)=Emax/Pin(si)表示MC在Aj处充满电池容量为Emax的传感器si需要的时间。在1个充电周期内，总的充电时间是各个锚点的充电时间的累加，即tcha=tc(A1)+tc(A2)+…+tc(Am)。每个充电周期中，MC在车站休息的时长为tres，则每轮充电任务的总时长为式(8)。

(8)

充电过程中应该保证后续的目标不会产生覆盖漏洞。MC在一次充电行程中需要响应M个目标簇的充电请求，此处忽略目标簇内子簇之间的行驶距离。待充电簇Cj的剩余寿命lj可根据簇内剩余子簇的个数和正在工作的子簇剩余能量计算获得

(9)

式中，Fj是簇内剩余处于睡眠状态的子簇个数；Ej是处于工作状态的子簇内传感器的剩余能量。

本文的问题可以定义为如下形式

(10)

s.t.∑si∈Sjφi，j≥Ψ，∀oj∈O

(11)

Pouttcha+Pmovtmov≤Emc

(12)

(13)

3 算法设计

为了求解上述问题，本文设计了基于单位子簇的充电选择算法(Charging Selection Algorithm based on Unit Sub-cluster，CSUS)。该算法包括3个过程：(1)将不同传感器聚合在目标点周围，构建目标簇；(2)将目标簇内的传感器节点根据监测增益划分成互斥的子簇；(3)子簇调度运行，对请求节点确定锚点位置并规划MC充电路径。随后，在基于全局的重聚类启发式算法(Entire-based Re-Clustering Heuristic algorithm，ERCH)中对CSUS进行优化。

3.1 构建均衡的目标簇

通常较大的目标簇能划分出更多的子簇，从而更好地平衡工作负载；而较小的目标簇可用子簇较少，会更加频繁地请求充电。本文提出的分簇算法每次贪心选择具有最小混合增益的目标簇，并将重叠区域内的部分节点分配进对应的目标簇。该算法通过对不同目标簇之间重叠区域内的节点进行合理划分来均衡相邻目标簇之间的混合增益，使目标簇之间能够划分出相近数量的子簇用于监测任务。伪代码如算法1所示，详细步骤如下：

步骤1计算节点到各个目标点的距离d(si，oj)，将只能监测一个目标的节点划分进各自的目标簇内，构成初始簇集合{Cj}，其中簇Cj负责监控目标oj并假定开启目标簇内全部节点。计算各个目标簇范围内的混合增益G；

步骤2对于可以监测多个目标的还未分簇的节点，根据其可以监测的目标的个数和种类进行分类。例如，可以监测oa和ob，将这种情况表示成集合[oa，ob]。假设第k类集合是lk，用|lk|来表示其中目标个数，将那些监测目标的个数和种类相同的节点划分成集合Γk，所有的Γk组成了升序排列的大集合{Γk}；

算法1 构建增益均衡的目标簇Input: S,O,rmaxOutput: {Cj}1.Build the original target cluster set Cj∈{C1,…,CM}2.Get hybrid gain of original target cluster denoted as Gj3.Build the set of tuples {lk}and the ascending set {Γk}4.for k=1,2,…,|{Γk}| do5. while Γk≠Ø do6. q←argmin{Gj},where j∈lk7. Get sensor node s∈Γk nearest to oq8. Cq←Cq∪{s},Gq←Gq+φs,k9. Γk=Γk{s}10. end while11.end for

步骤3从Γ1遍历分类好的重叠节点集合{Γk}，对于集合l1中的目标点，找到目标簇中具有最小混合增益的充电目标oj。从集合Γ1中选择一个靠近oj的节点s把它分配给簇Cj并更新混合增益，然后将s从集合Γ1中移除。对于集合Γ1中剩余的元素重复执行上述过程，直到集合中的元素都分配完成。整个迭代过程在Γ2，Γ3，…，Γk上顺序执行，直到所有重叠区域的节点分配完成，得到各个增益均衡的目标簇。

3.2 簇内子簇划分

为了有效调度目标簇内的节点，本节需要从每个目标簇中划分出多个工作子簇来服务于网络中的目标监测任务。

伪代码如算法2所示，划分过程中，每次从目标簇周围最近的一个节点开始搜索，在搜索的过程中根据最短距离优先的原则构建子簇，并计算联合监测增益，判断是否达到指定要求，达到要求后放弃搜索。当前子簇构建完成后，将选出来的点从目标簇中剔除，否则继续添加新的距离当前子簇内所有节点距离都小于D的节点，直到监测增益≥Ψ。然后选择剩余传感器中距离目标点最近的节点开始构建下一个子簇，重复上述过程直到目标簇内剩下的节点不能满足Ψ或目标簇内节点为空时，停止构建过程。在每个目标簇内构建Kj个待工作子簇，整个网络中的子簇集合是{B1，B2，…，BM}。

因此各个目标点周围的子簇数量

3.3 子簇充电调度

在子簇划分过程中，保证了子簇内的多个节点间的距离≤D，因此MC能够停靠在子簇中的某个位置，进而对能量耗尽的单位子簇进行有效充电。本节中选取子簇内所有节点位置的平均值作为锚点，通过这种策略来对子簇内的节点提供相似的充电功率，平衡了子簇中各个节点的充电时间。在调度过程中，距离车站更近的子簇具有更高的优先级。算法1中使用了增益均衡的策略，相近。在每个目标簇内，调度K个子簇，其中K=minKj表示所有目标簇内子簇数量的最小值。本文将使用经典的Christofides算法来求解N个锚点之间的最短TSP路径，并用Lmc=Christofides(N)来表示。

测试样本向量u在字典样本矩阵H中的稀疏表示系数x，即用正交匹配追踪算法求解最小化问题，其中，φ为允许最小的迭代误差。

按照优先级激活子簇，当目标簇内的子簇数量低于ηK时发出充电请求，MC对每个目标簇内的χ个子簇进行充电，χ的数值将在模拟实验中进行确定。根据χ个子簇内的锚点位置可以计算出每个锚点处的停留时间之和，即充电时间tcha，然后根据Christofides(AP)求出MC的充电路径，进而求出tmov。当MC对子簇进行充电时，簇内剩余K(1-η)个子簇仍可调度，当另外的χ个子簇耗尽能量后再次发出充电请求。MC当前1次充电循环中的休息时间可以表示为式(14)。

(14)

上图中简易展示了子簇调度和充电的过程。如图2中所示，两个目标簇中各有4个可用调度的子簇，充电过程为：

步骤1如图2(a)所示，c1、c′1和c2、c′2能量相继耗尽，顺序激活子簇c3、c4和c′3、c′4。MC对c1、c′1和c2、c′2进行充电，充电完成后MC在depot休息，充电周期为T1，休息时间为tres1；

步骤2如图2(b)所示，c3、c′3和c4、c′4能量相继耗尽，激活子簇c1、c2和c′1、c′2，MC对c3、c′3和c4、c′4进行充电，充电完成后MC在depot休息，充电周期为T2，休息时间为tres2。

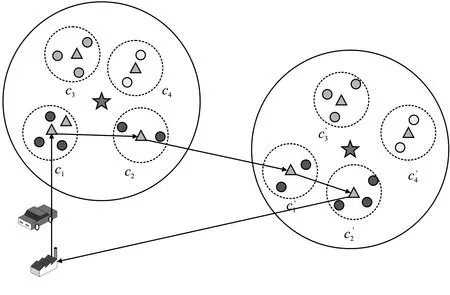
(a)

接下来的充电过程不断重复步骤1、步骤2，整个网络保持ε监测覆盖持久运行。步骤1、步骤2中的短周期T1和长周期T2组成了固定充电周期T，MC的休息时间占比为(tres1+tres2)/T。

3.4 充电调度优化

在算法2的子簇划分过程中，“子簇内节点间距离≤D”的要求会导致过剩增益增加并减少最终划分出的子簇个数。在本章节中，划分子簇时，适当降低算法2中的距离严格程度，将子簇内节点之间的相互距离控制在1.5D范围内。如图3所示，算法2在网络中节点密度较大的情况下，不同的充电子簇之间存在重叠。在章节3.3中，以子簇为单位进行充电，并没有从请求节点整体考虑锚点位置。如果对图3中两个重叠子簇整体考虑锚点位置，则可以将锚点数量从4降低到2，优化之后的单个锚点可以覆盖更多的节点，从而更好地发挥多节点充电的优势。本节通过ERCH算法将网络中所有需要充电的节点重新聚类来对锚点进行优化。

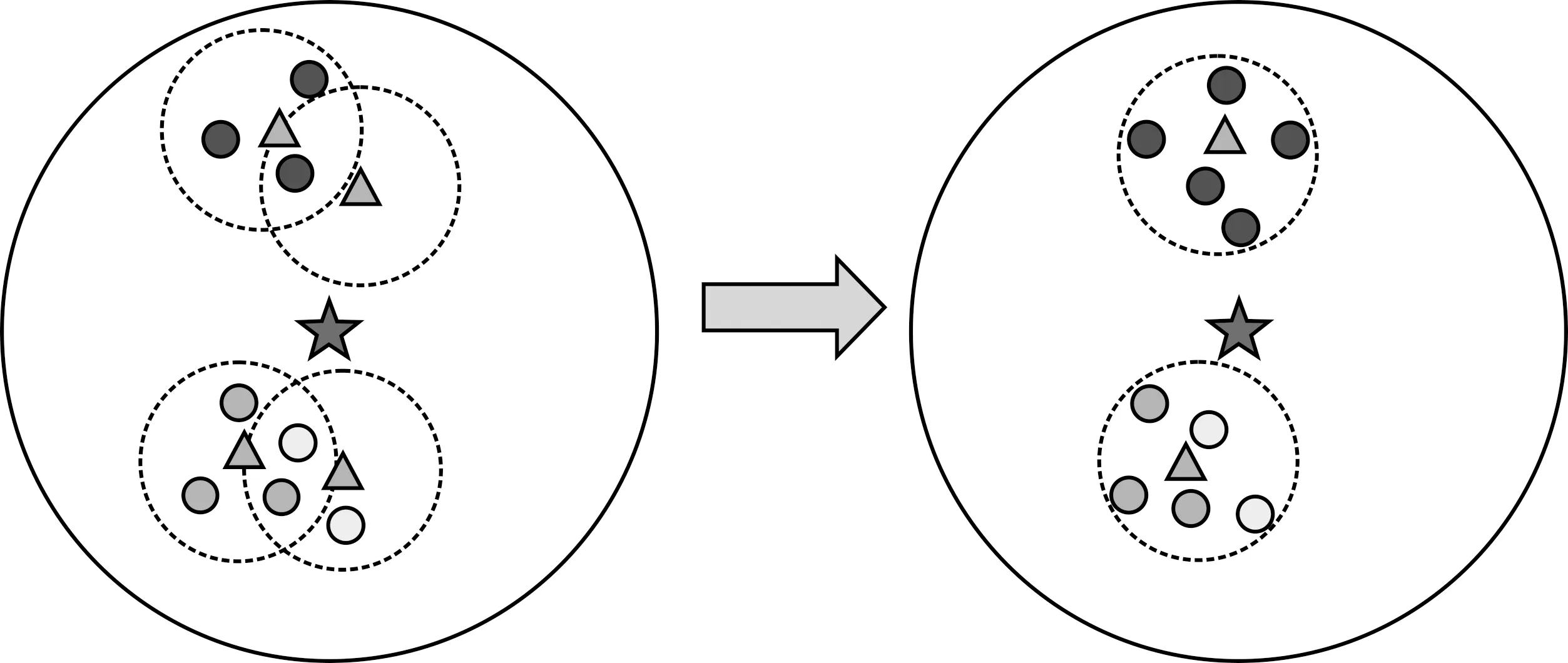
图3 锚点优化 Figure 3. Anchor point optimization

伪代码如算法3所示，详细步骤如下：

步骤1构建初始充电形心集合Vinit。首先构造图G=(Vs，E)，顶点集合Vs对应需要充电的子簇内的节点，在距离≤D的两个顶点之间添加边，E是边的集合。每次选择G中度数最大的点，加入Vinit作为初始充电簇形心，删除该点以及其邻接点的边，直到G中没有边为止。如图4所示，经过步骤1，节点2和节点4被选为初始簇形心；

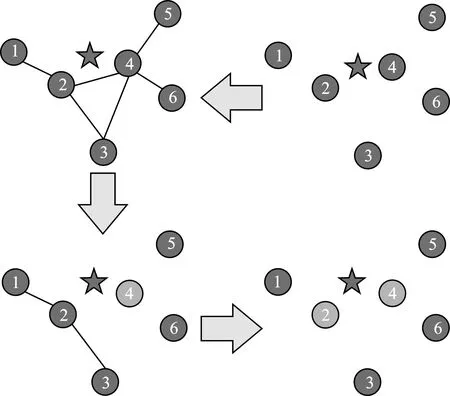
图4 构图和选择初始形心 Figure 4. Composition and selection of initial cluster centroids

步骤2迭代分配过程。集合Vinit中的每个节点代表一个充电簇的初始形心，将剩下的节点中距离当前形心≤D的节点添加进充电簇。计算划分到充电簇中的所有节点新均值，作为新的充电簇形心。重复迭代至划分结果处于稳定状态，生成充电簇集合Λ1；

步骤3处理剩余节点。经过步骤2之后，请求节点集合中仍可能存在距离≤D的节点，需要对剩余节点进行再次划分。先让每个剩余节点单独构成簇，将距离≤D的独立簇合并。更新簇的形心并使用新的簇形心重新分配所有节点。重复迭代至分配结果不再变化，生成充电簇集合Λ2和剩余的孤立节点集合Y。

算法3 基于全局的重聚类启发式算法Input: request node set Vs,DOutput: Λ1,Λ2,Y1.Constructing graph G=(Vs,E)2.Get set Vinit and create initial cluster set C by Vinit3.repeat4.for each cluster Ci∈C do5. for each node vj∈Vs do 6. if isclustering(vj)=false && di,j≤D then 7. Ci=Ci∪vj8. isclustering(vj)=true 9. end if10. end for11.end for12.Update the centroid of each cluster13.Reset the clustering state of each node to false in Vs14.until the results are stable15.Λ1=C16.if exist di,j≤D between the nodes vi and vjin Vs then 17. Calculate cluster set CR by Vs18. Traversing the cluster and merging the cluster19. repeat20. Update centroid and clear each cluster Ci in CR21. Reset clustering state of each node to false in Vs22. Redistribute node vi∈Vs using new cluster centroid23. until the results no longer change24. Λ2=CR25. Add all isolated nodes in set Vs to set Y26. return Λ1,Λ2,Y27.end if

经过上述步骤，充电节点被划分成充电簇Λ=Λ1∪Λ2∪Y，它包含所有的充电锚点，而Y中的孤立节点将被单独充电。充电过程中，MC按照距离顺序选择Λ中的锚点进行充电任务。ERCH算法中的其余过程与CSUS算法保持一致。

4 仿真实验分析

本文通过仿真实验对本文模型及两种不同充电策略的优越性进行验证：首先设置不同的参数来探讨参数对充电小车休息时间比例的影响；随后将本文提出的CSUS算法和ERCH算法与单节点充电模型(Single-Node Charging，SNC)进行对比。

4.1 实验参数设置

本文在50 m×50 m的目标区域中随机部署500个传感器节点和5个目标点，将depot的位置设置在平面区域的左下方。实验在Windows10系统的IntelliJ IDEA平台上使用Java语言进行模拟。硬件环境为CPU Intel 8086k、频率4.0 GHz、6核12线程台式机。为保证实验可靠性，所有实验均进行100次仿真，实验结果取平均值。表1中给出了实验相关的参数设置。

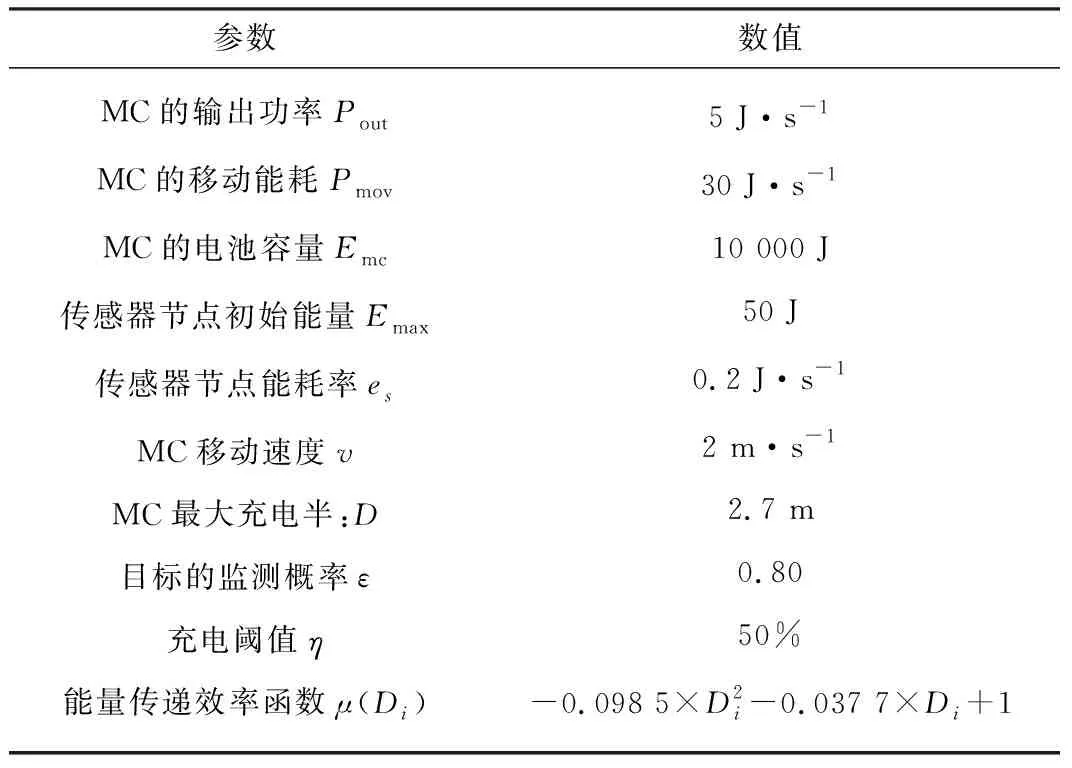
表1 实验参数

4.2 实验结果与分析

如图5所示，在子簇由1到4的纵向比较中可以看到，在一定范围内满足更多子簇的充电需求可以带来更高的休息时间占比。但在实际实验中，4子簇的网络成功率仅有20%左右，且其休息比例同3子簇相差不大，这是因为满足更多子簇的充电需求对构建子簇和MC的能量要求更高，限制了实验成功率和最终适宜的子簇充电个数。根据图5中的实验结果，在后续比较中均采用3子簇的充电策略，而现实场景中则可以根据MC的容量进行调整。

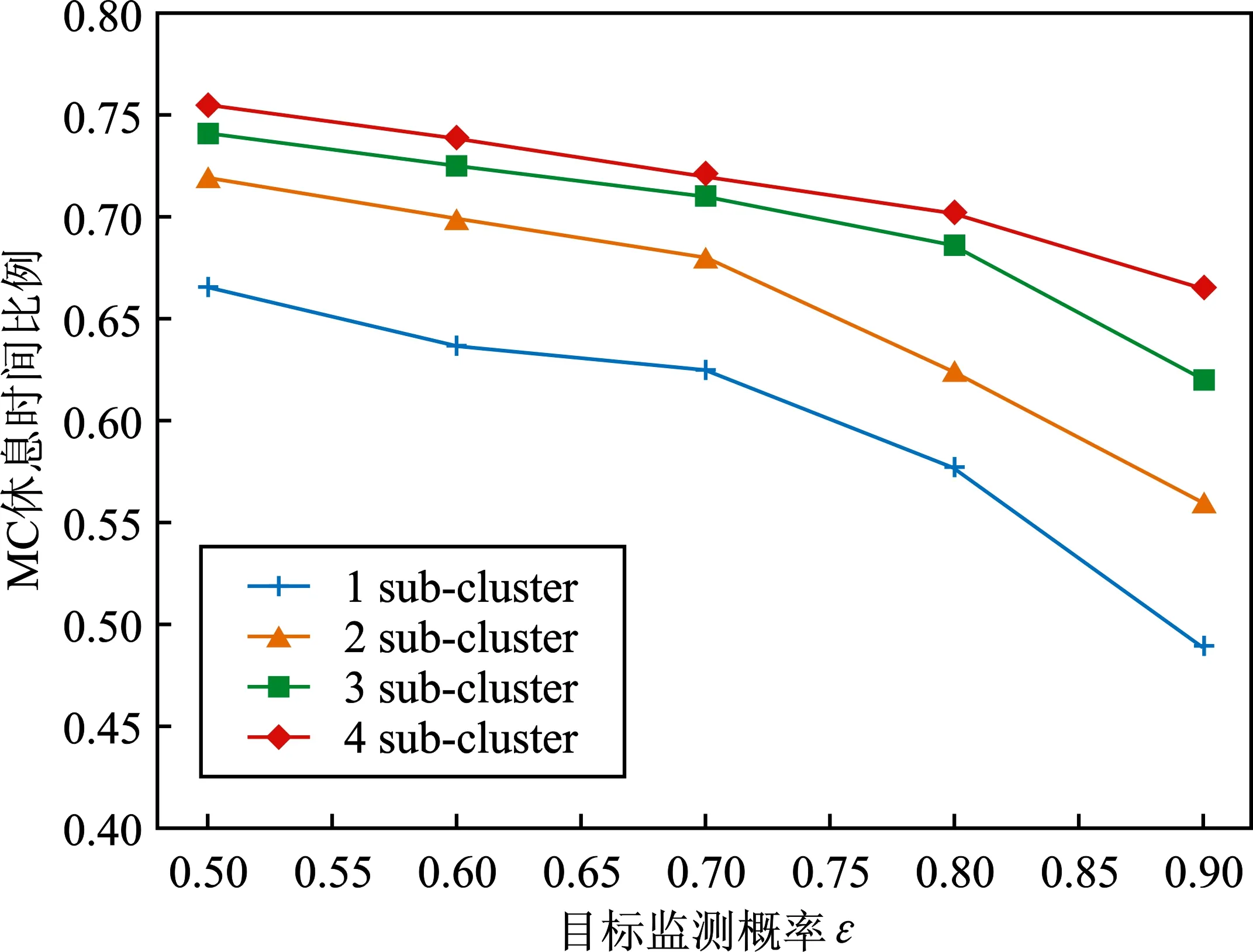
图5 休息比例与子簇充电个数的关系Figure 5. Relationship between the rest ratio and the number of charged sub-clusters

由图6中可以看出，随着区域面积从40 m×40 m增加到80 m×80 m，MC的休息比例逐渐降低。因为区域面积的增大导致节点密度减小，子簇之间和目标簇之间的距离变大，MC的移动时间增加，稀疏的子簇也会使得MC充电时间增加，从而导致MC休息比例的减小。此外，ERCH算法优于CSUS算法，但随着网络规模的扩大，这种差距逐渐缩小。这是由于ERCH在节点密度较大时可以有效减少锚点的个数，使充电效率更高。但由于目标簇内不再存在较多的重叠子簇，因此这种优势随着区域的变大逐渐缩小。

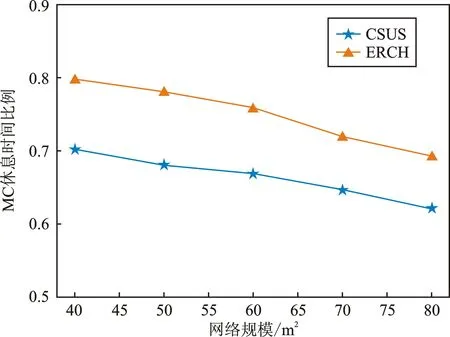
图6 休息比例与网络规模的关系Figure 6. Relationship between the rest ratio and network size

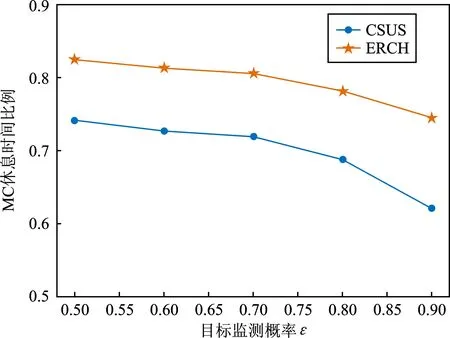
图7 休息比例与覆盖要求的关系Figure 7. Relationship between the rest ratio and coverage requirement

由图7中可以看出，目标的概率覆盖要求从0.5增加到0.9，MC的休息比例逐渐越低。这是因为随着监测概率的增大，子簇内包含的节点个数也随之增大，每个子簇内需要满足的节点的充电需求增多，导致充电时间的增加，进而降低了MC休息比例。此外，算法ERCH经过优化，在休息时间比例上始终优于算法CSUS。当监测概率由0.8增加到0.9时，两个算法之间的差距更大，这是因为更高的覆盖要求让每个子簇内的节点更多，算法ERCH的优势表现得更加明显。

本文对两个算法与单节点充电模型进行对比，在100 m×100 m的区域内随机部署1 500个传感器和10个目标。由图8中可以看出，随着目标概率覆盖要求从0.5增加到0.9，3种策略中的MC休息比例均有所下降，且算法CSUS和算法ERCH优于SNC。优化算法ERCH相较于SNC提升了10%～15%。这是因为，SNC在进行充电服务时需要逐个访问每个节点，而在较为密集的网络中，算法CSUS和算法ERCH中的充电模型每次可对多个节点同时充电，充电效率更高。

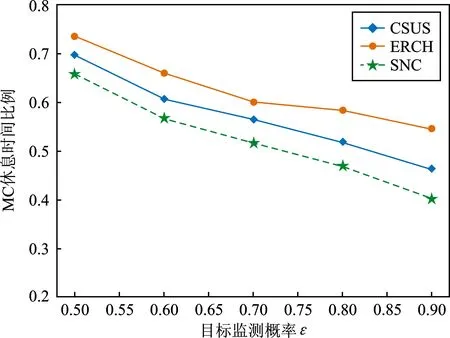
图8 休息比例与充电模型的关系Figure 8. Relationship between the rest ratio and charging model

5 结束语

本文研究了ε概率覆盖传感网络中的最大化MC休假时间比例问题，并提出了一种CSUS算法。CSUS算法包括3个过程，首先通过基于均衡增益的目标簇划分算法有效平衡了不同目标周围的传感器工作负载；然后在每个目标簇内按照贪心思想划分出多个子簇；最终在子簇充电调度算法中调度不同的子簇，并确定锚点来进行充电。本文在ERCH算法中通过放宽子簇划分的距离限制并对充电节点整体进行重聚类的方式对CSUS进行了优化。仿真实验对两种算法的有效性进行了验证，并将新方法与单节点充电方式进行了对比。由于单MC 的服务能力有限，因此在未来实际工作中，需要考虑利用多个MC进行协同充电。