管壳式换热器壳程流体流动与传热的数值模拟研究
2022-06-16瞿莹王华玲蒋志鹏吴宏亮
何 超,瞿莹,王华玲,蒋志鹏,吴宏亮
(1.淮阴工学院 机械与材料工程学院,江苏 淮安 223003;2.淮阴工学院 江苏省先进制造技术重点实验室,江苏 淮安 223003;3.淮安市鼎新电子有限公司,江苏 淮安 223200)
管壳式换热器广泛应用于电站、船舶、石油化工及制冷空调等领域的换热设备中。而管壳式换热器在这些领域工作过程中,往往存在着大量的相变换热及两相流动问题,对换热器本身的传热效率及使用寿命等有着至关重要的影响[1]。统计数字表明,在工业用换热器中有近50%的换热器均在壳程存在两相流动,诸如重沸器、凝结器和蒸发器等[2]。
管壳式换热器壳程结构复杂,流体在壳程的流动也很复杂,使用实验方法很难得到换热器内部具体的流场和温度场,且耗时和昂贵,传统的理论计算基础上进行建模实验验证的设计方法显得越来越低效。随着计算机技术的不断升级以及CFD技术的快速发展,采用数值模拟的方法来对换热器进行流体与传热的特性计算,预先得出传热与阻力的准数关联式,为实际尺寸模型的设计提供可靠的依据成为了一种趋势,是继实验方法后的一种重要换热器研究手段[3]。因此,以常用的管壳式换热器(弓形折流板换热器)作为研究对象,该换热器壳程流体发生冷凝相变及两相流动,采用CFD模拟软件建立管壳式换热器三维实体模型,对壳程流体的速度场、温度场和冷凝水体积分布情况进行了分析研究[4]。
1 换热器壳程流场数值模拟
1.1 基本控制方程
流体介质的流动必然会受到物理学守恒定律的支配,流体介质的流动要满足三个基本的物理量守恒定律:物质的质量守恒定律、物质的动量守恒定律和物质的能量守恒定律。如果流体流动属于湍流流动状态,则还要满足湍流输送方程。壳程介质为饱和水蒸气,其换热后发生冷凝,涉及传质和相变,因此还需要添加一个组分质量守恒方程。
(1)质量守恒方程(连续性方程)
对于不可压缩流体,ρ为常数,故不可压缩流体三维流动的质量守恒方程可表示为:
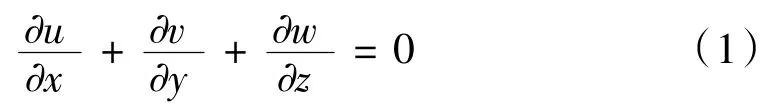
(2)动量守恒方程
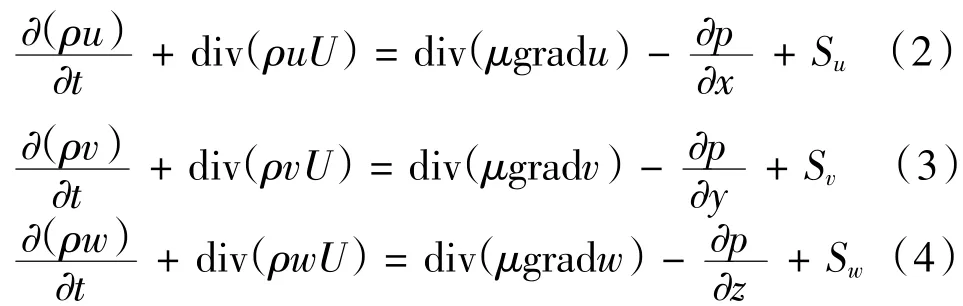
(3)能量守恒方程
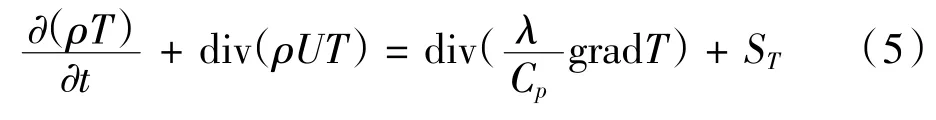
(4)组分质量守恒方程
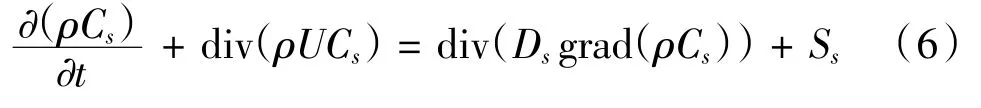
式中:U为速度矢量,u、v、w分别为速度矢量U在x、y、z坐标方向的分量,ρ为流体密度,t为时间,μ为流体的动力黏度,p为压力,Su、Sv、Sw三个动量守恒方程的广义源项,T为温度,λ为流体的导热系数,Cp为比热容,ST为粘性耗散项,Cs为组分s的体积浓度,Ds为扩散系数,Ss为系统内s组分质量的产生率[5]。
1.2 计算模型
进行数值模拟的换热器为普通管壳式换热器,换热器结构为单管程、单壳程和单弓形折流板,其结构尺寸见表1。

表1 换热器结构尺寸
1.3 计算模型与计算条件的简化
由于换热器壳程结构复杂,在保证相关物理量准确的前提下,建立模型时作如下简化假设:(1)折流板与换热管、折流板与壳体之间的间隙忽略不计;(2)拉杆、定距管、不凝气出口管等结构忽略;(3)流体流动和传热过程稳定,不考虑污垢热阻;(4)流体视为不可压缩流,各向同性且连续;(5)气相看作纯组分,忽略液膜热阻[6]。
计算边界条件的简化:(1)壳体光滑,无滑移边界条件;(2)假设换热管外壁温度为恒温;(3)中心面为对称边界;(4)速度进口和压力出口边界条件,出口表压力为0 MPa。
1.4 几何模型建立及网格划分
该软件以有限元法为基础,采用迭代方法进行数值模拟计算,需要对模型进行网格划分。建立的模型为三维模型,网格划分时运用对称特性,实际计算时只取一半的模型进行,从而减小了模型尺寸,降低了计算成本。简化后的几何模型如图1,划分完的网格的模型如图2。
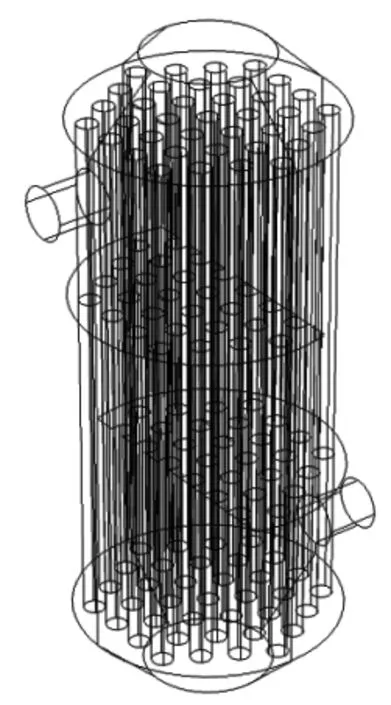
图1 简化几何模型
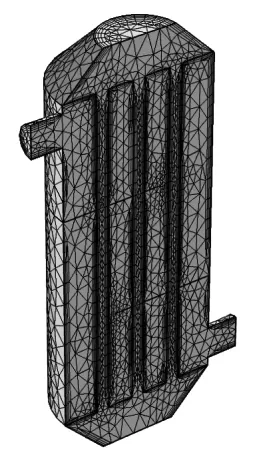
图2 网格划分
1.5 求解设置
1.5.1 物理场选择
换热器壳程和管程流体均为湍流流动,同时热流体和冷流体之间存在传热情况。对于上述情形,该软件的流体流动模块下设置了非等温流动,再下设湍流k-ε物理场,该接口将流体传热与湍流k-ε接口相结合,自动添加了非等温流动多物理场耦合,可用于模拟传热与流体流动之间的耦合。在湍流k-ε物理场中,物理模型选择了传统雷诺平均模型(RANS)的k-ε二方程模型,流体为不可压缩流动,壁处理为壁函数。
1.5.2 定义边界条件
边界条件设置为速度入口和压力出口边界条件,开启重力条件,重力加速度方向为-z轴方向。壳程饱和蒸汽入口速度为0.4 m/s,入口温度为155℃,管程冷却水入口速度为0.01 m/s,入口温度为50℃。在流体传热物理场中,环境温度为20℃,环境绝对压力为1个标准大气压,定义换热器所有壁为薄层。壳程饱和蒸汽相变温度为151.85℃,冷凝潜热2108.4 kJ/kg。湍流条件采用湍流长度和湍流强度,湍流长度尺度取0.07r,其中r为入口通道半径,湍流强度I通过经验公式(7)求得。除了对称面,其余外部边界都是热绝缘壁面。在进行数值模拟时,因为出口常常会发生回流,因此使用压力出口边界来代替速度出口边界条件以获得更好的收敛效果,并设定出口为法向流并抑制回流。壁面的边界选择无滑移的刚性壁面,除了对称面,其余所有外部边界都是热绝缘壁面。

2 计算结果分析
2.1 速度流线图
由图3(a)可见由于入口处截面积较小,流体流入壳程时,由于流动截面积增大,流速快速降低。壳程内流体由于换热器壳壁和折流板的作用,整体呈“Z”字形向出口流动,在折流板的缺口下方,形成了明显的旋涡,而且流速较低,在折流板根部靠近壳壁处,则较少有流线经过,说明在该处存在流动死区,区域内流体经过量较少,传热影响明显。图3(b)显示由于换热管的阻挡作用,流体沿换热管间隙向壳程内部流动,当遇到壳壁时,流体沿壳程斜下方流动。
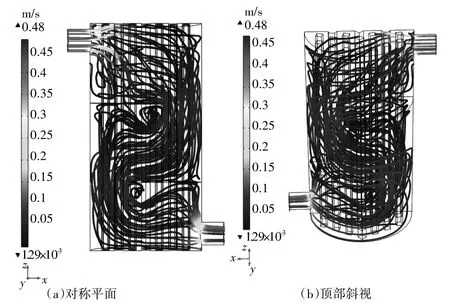
图3 壳程流体的速度流线图
2.2 温度分布图
图4(a)显示在换热管管壁处出现了浅色区域,主要集中在第一折流板根部的流动死区和第二折流板缺口下方的旋涡区,这是因为这两个区域内,新进的流体流量少,流速低,区域内流体与换热管内冷流体换热时间相对较长,新进流体补充不充分,导致该区域内壳程流体温度比附近区域要低,与管程冷流体间的相对温差变小,根据稳态传热基本公式可知,该区域的传热量较高温区域要低。从图4(b)中可看出,高温饱和蒸汽从换热器入口接管进入换热器后,温度逐渐降低,总体的变化趋势也呈“Z”字形,这说明温度的分布与速度流线有着直接的关系,同时折流板根部流动死区和缺口下发旋涡区,由于传热效果差,温度比同高度的其他区域要低。
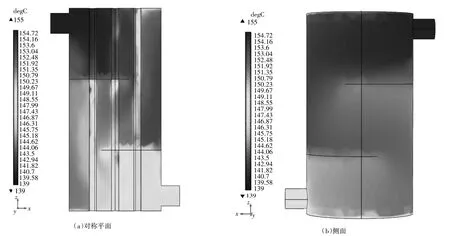
图4 壳程流体的温度分布图
2.3 冷凝水体积分布图
图5(a)可以看出,壳程进口段至上侧的折流板区域,凝结并不明显,这是因为管程流体经换热器下部换热后,流体温度较高,与入口蒸汽温差较小,传热系数较低,且新进入壳程的饱和蒸汽流速快,使得冷凝形成的湿蒸汽向换热器下方移动,而在上侧折流板至壳程出口段,蒸汽冷凝快速发生。在换热管管壁处,冷凝水的体积分布也比附近区域要高。
图5(b)可以看出冷凝水的体积分布也是呈“Z”字形分布,与壳程流体速度流线和温度分布情况相吻合。由于不断通入壳程入口的高温蒸汽持续给前方流入换热器内的气体加热,进口处凝结量较少,沿速度流线方向上,冷凝水体积占比从进口到出口逐渐升高,在出口处及下管板附近,该区域体积分数接近1,说明饱和蒸汽基本完全冷凝。在折流板背部的流动死区及折流板缺口背部的旋涡区,冷凝水的体积占比比同高度的其他区域要高,这是因为该区域新进的高温蒸汽流量少,蒸汽温度较低,与管程冷流体换热后,凝结量较大,又因为该区域流体流动缓慢,凝结形成的湿蒸汽不能快速流动离开该区域,故区域内冷凝水的体积分布大。
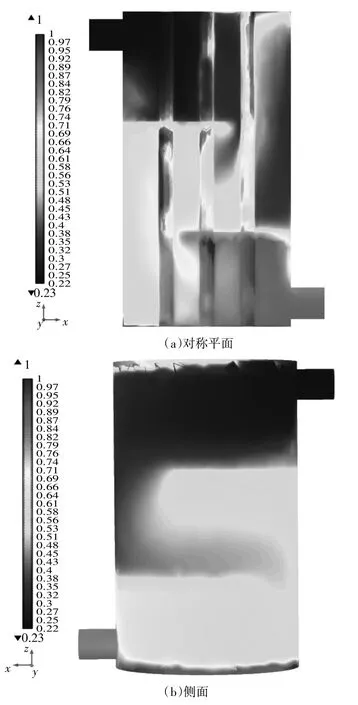
图5 壳程冷凝水的体积分布图
3 结论
以常用的弓形折流板管壳式换热器为研究对象,通过对换热器壳程三维流场的流动与传热进行数值模拟,得到以下结论:
(1)高温饱和水蒸气由入口进入换热器,由于换热管的阻挡,流体沿换热管间隙向换热器壳壁流动,同时在折流板作用下,呈“Z”字形向换热器出口流动。换热器壳程内部的温度和冷凝水体积分布也随流体流动情况而变化,整体也呈“Z”字形,与流体速度流向正相关。
(2)在折流板缺口背部区域出现旋涡区,该处流体流速较低,同时折流板根部出现流动死区,这两个区域温度比同高度的其他区域温度低,因此冷凝水体积分布较大,说明低流速区域冷凝现象较明显,不利于传热进行。
研究结果有助于对相变换热情况下的管壳式换热器壳程流体流动增加认识,并为结构设计和优化提供参考。
