模块化的应急物资库存量优化模型研究*

胡春玉 李星毅

（江苏大学计算机科学与通信工程学院 镇江 212013）

1 引言

自然灾害是全球面临的共同挑战，而应急物资的储备问题一直是应对突发灾害工作中的核心内容。我国是世界上遭受自然灾害影响最严重的国家之一，进入21 世纪以来，我国遭受特大地震、低温雨雪灾害、泥石流等不同灾害，目前我国中央级的救灾物资储备库已由10个增加到24个，部分省、市、县建立了地方救灾物资储备仓库，初步形成抗灾救灾物资储备体系［1］。

近年来，国内外学者针对应急物资预储的问题做了不少研究，如LIU Jie 等［2］考虑了救援物资分配的合理性和有效性，通过MWL-EMA来规划应急物资的储备问题并构建了基于成本的应急物资储备模型。ZHANG Jianghua 等［3］基于线性规划和优化网络，构建了多物资库和多受灾需求点储备模型。Das 和Hanaoka［4］用连续的均匀分布函数来表示救援中订货的提前期和需求的不确定性，在此基础上研究了物资储备点的订货点问题，有效减少了灾后因为物资的缺口而造成的损失。朱佳翔、蔡建飞等［5］针对灾害信息的不确定性并结合区间二型梯形模糊集理论和比例分析法，构建了应急物资储备动态协同决策模型，给出了有效的应急物资储备策略。林琪和赵秋红等［7］针对应急救援的阶段性特点，分析了响应期物资和恢复期物资间的关联关系，构建了基于关联与替代关系的应急物资储备量决策模型。丁斌等［10～12］从合作博弈和政企合作的两个角度出发，研究了政府与供应商共同合作进行的应急物资储备策略模型。

不同等级的灾害所需要参与救援的储备库等级是不同的，而不同等级的储备库的保障水平也有所不同，此外，某些物资需要共同辅佐才能更好达到救援效果，鉴于上述研究未考虑到的问题，本文旨在结合物资的模块性和储备库的不同等级能力，构建以物资的需求满足率最高和储备系统总成本最小为目标的数学模型，并采用概率扰动策略设计了NSGA-II改进算法进行模型求解，得出不同模块的物资在不同等级储备库中的最佳储备量。

2 模型建立

2.1 问题描述和假设

以我国形成的中央、省、市、县四级储备体系为研究背景，将储备库划分为四个等级，采用行政隶属结构来划分区域储备库层级关系，假设目标区域内有若n 个不同等级的储备库R={Ri|i=1，2，…，n}，受灾点附近有m 个物资集散中心C={Cj|j=1，2，…，m}。提供物资保障的储备库等级参考田卫东［13］研究的对于储备库参与调运的层级问题，遵循先地方后国家、就近调运的原则。灾害发生后，受灾点先向当地储备库和其所在地本级储备库申请物资救援；需求不能得到满足时再依据行政管辖关系向上级储备库和与受灾点同级的其他储备库申报物资；如果依然不能满足需求，再向更高级别的储备库申请援助，依次下去直至国家级层面的储备库。

不同于仅仅只考虑单类物资的储备量决策问题，本文引入军事物资中的单元化概念［14～15］，在物资储备的过程中，将具有一定依赖关系的物资进行模块化处理，即按一定的数量比例将某几种物资进行打包，形成物资模块。灾害的种类影响到物资存储的种类，结合过往灾害救援中的先验知识，设定物资g1，g2，…，gc按照比例a1，a2，…ac组成物资模块Ak，即物资模块Ak满足关系Ak={a1g1，a2g2，…，acgc}，存在单类物资的存储量与所属物资模块的量构成一定的比例关系，并且同一模块的物资达到受灾点的时间间隔在一定的范围内。

灾害发生的初期很难准确获取物资集散点的需求量，往往是估计性的描述语言，本文采用三角模糊数来描述一个受灾点对物资的需求量，物资集散中心Cj对第s种物资的需求量是一个三角模糊数，，其中：0 和是三角模糊数的上下界，是偏好量，即集散中心Ci的需求预置量。集散中心的物资需求偏好量是参考刘宗熹提出的方法来设定的［17］，首先确定储备区内的总储量S，由灾害范围R、区域内人口密度ρ、人均需求量决定，S=R×ρ×d，再根据各储备节点的需求指数We确定各集散点的需求偏好量，需求指数由一个地区的经济指数ei、人口指数pi和交通指数ti确定。将每个集散中心的需求量的隶属度函数设计为

其中为储备库Ri为集散中心Cj提供第s种物资的数量。

基于以上描述有如下假设：

1）区域内各个储备库的位置、数量和最大容纳体积已知，物资储备量以每人份为单位，在同一个区域内的各储备点可以相互调配应急物资，每个储备库可以同时向多个集散点提供物资。

2）各个储备库到达集散中心的时间已知，忽略道路拥堵、毁坏、运输工具和装载空间等限制问题。

3）总成本主要考虑建库成本、管理成本和运输成本并且不考虑物资超出保质期而造成的经济损失。

2.2 模型构建

基于上述考虑和假设，构建了如下优化目标和约束条件：

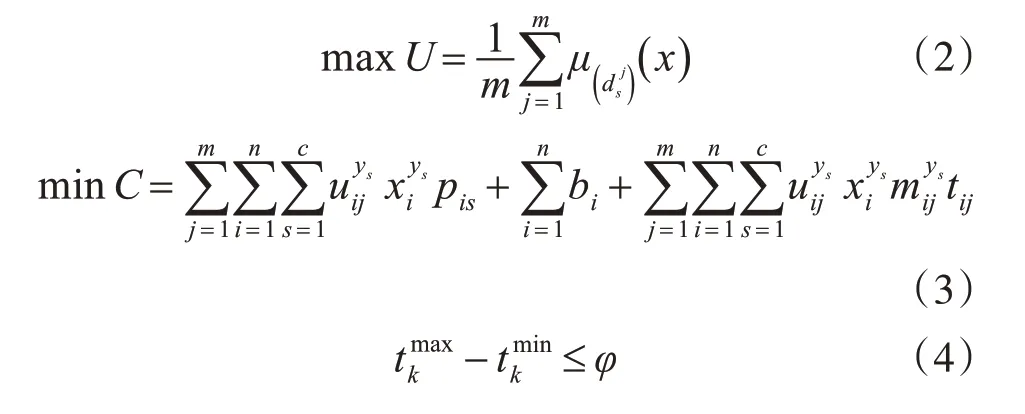
目标函数（3）最小化储备总成本，第一项是储备管理成本，第二项是投入建设储备库的总成本，第三项是物资运输成本。其中pis为储备库Ri中物资s 的单位储备成本；bi为储备库Ri的固定建设成本；为从储备库Ri运输物资ys到集散中心Cj的单位运输成本；tij为储备库Ri到集散中心Cj的运输时间；为物资ys在储备库Ri中的储备数量，是决策变量。

约束条件（4）保证同一模块的物资到达集散中心的时间差在一定范围内；其中为物资模块K种物资最慢到达集散中心所用的时间；为物资模块K种物资最快到达集散中心所用的时间。

约束条件（5）表同一模块内的各种物资在各储备库的储备总量符合一定的比例关系。

约束条件（6）表示库存物资储备的体积少于储备库的容纳体积，其中vs为物资s 的单位体积，wi为储备库Ri的最大容纳体积。

约束条件（7）表示储备库Ri中物资s的存储量不大于提供给集散中心Cj的数量。

约束条件（8）表示0-1决策变量，取值为1的时候，表示储备库Ri向集散中心Cj提供物资ys，取值为0 时，表示储备库Ri不为集散中心Cj提供物资ys。

约束条件（9）保证至少有一个储备库为集散中心Cj提供物资保障。

3 模型求解

3.1 改进NSGA-II算法

多目标优化问题不同于单目标优化问题，当只有一个目标函数时可以很容易找到最好的解，但是当存在多个目标函数时并且这些目标存在冲突问题，人们很难找到同时满足所有目标函数的最优解。带精英策略的非支配排序遗传算法（Elitist Non-donminated Sorting Genetic Algorithm，NSGA-II）在求解多目标优化问题上表现出较大优势，但是求解过程中随着迭代次数的增加，容易收敛到局部最优。因此，为了增强后期的种群多样性和降低陷入局部最优的可能性，本文在种群更新过程中加入概率扰动策略来降低陷入局部最优的概率，借鉴陈闯［18］设计的一种简单有效的扰动概率策略以及粒子群算法中粒子每次更新都会利用当代最优个体的思想。设计扰动概率公式为

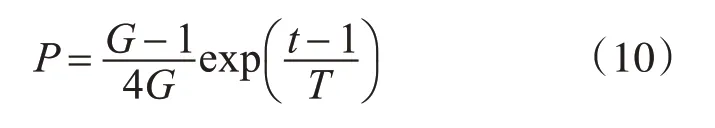
其中：P 是扰动概率；G 是优化目标的维度；T 是最大的迭代次数。借鉴粒子更新公式设计如下扰动公式：

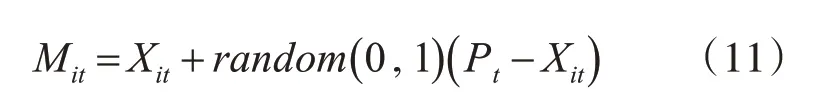
其中：i=1，2，…，N为种群规模，Mit为扰动后的个体，Xit为第t代种群中第i个个体，Pt为第t代中的最优个体。扰动后的个体基于贪婪准则更新，更新公式如下：

其中F(X)是表示个体X的目标函数值。

3.2 算法实现过程

随着NSGA-II算法的迭代次数增加，算法求解会逐渐收敛，通过引入扰动概率来提高收敛于局部最优的能力，其算法步骤如下。

第1 步：参数初始化。随机生成规模为N 的种群Pt，当前迭代次数为0。

第2 步：通过扰动策略产生子代种群Qt。利用式（10）计算扰动概率，通过与初始化随机参数的比较判断是否进行扰动，如需要则根据式（11）和式（12）分别进行个体扰动和个体更新，然后进行选择、多点交叉、变异操作产生子代种群Qt。

第3步：非支配排序。将Pt和Qt合并为二倍种群Rt，对临时种群Rt进行快速非支配排序并计算个体拥挤距离。

第4 步：通过拥挤距离比较算子和精英保留策略选出N个个体，组成下一代种群Pt+1。

第5步：跳至步骤2，并循环直至达到最大迭代次数结束。

对应的算法流程图如图1所示。

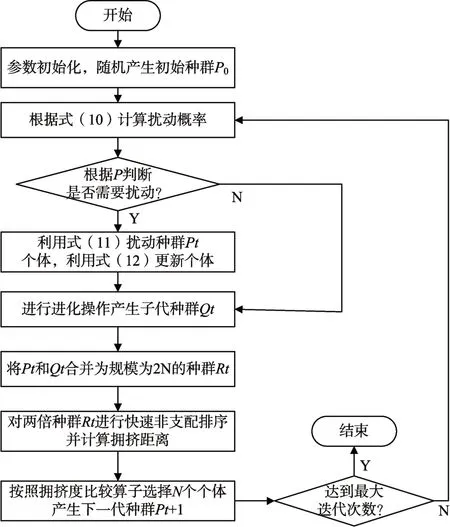
图1 改进后的NSGA-II流程图

4 仿真算例

假设某储备区有中央级储备库R1，省级储备库R2，市级储备库R3～R6，县级储备库R7～R12，4个集散中心C1、C2、C3和C4。表1 是各储备库的固定建设费用和容纳量；表2 是各储备库到达集散中心的时间。为简单起见，实验主要以民众消耗品为主，满足灾后三天的物资基本保障，其中模块化物资A1由棉被、帐篷、棉衣裤以2∶1∶4 的比例组成模块化物资。

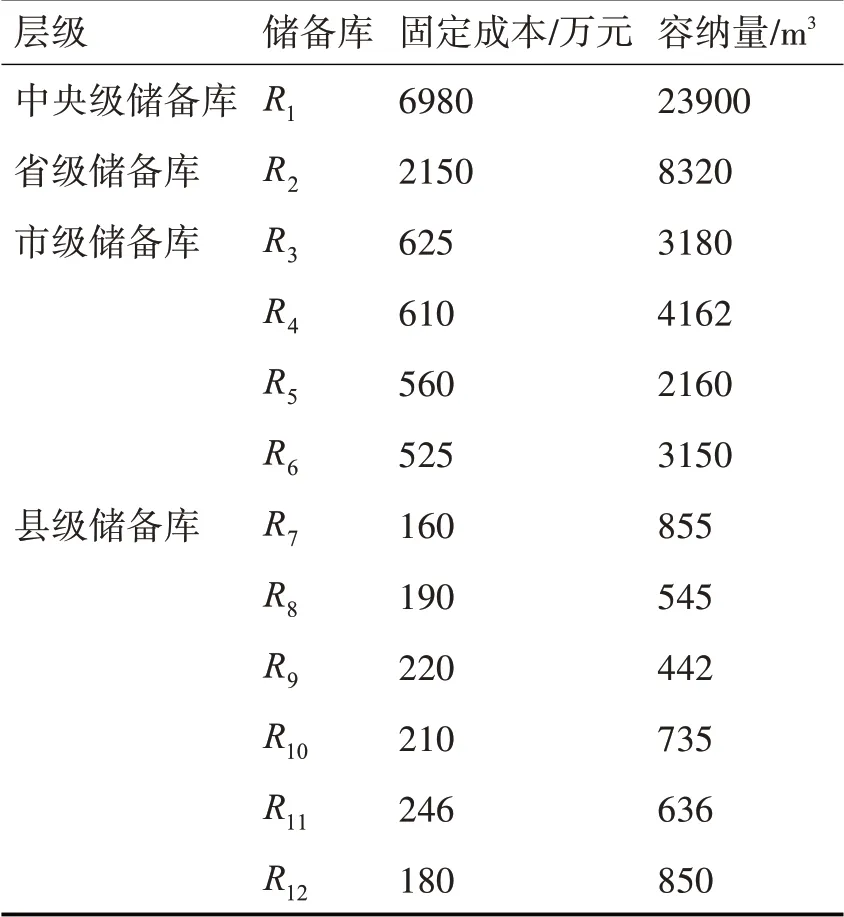
表1 拟建储备库的基本情况

根据国家对自然灾害的应急响应等级划分，用改进的NSGA-II 算法对需要启动Ⅰ级响应的地震场景的算例模型进行优化，设置交叉概率为0.9，变异概率为0.2，种群大小100，迭代次数200，经计算得到12 个有效方案，结果如图2 所示，其中横坐标为目标函数成本，纵坐标为满足率函数。通过观察可知成本和物资需求满足度是相互制约关系，随着满足率的提高，所需要的储备成本和运输成本也跟着增加，成本投入太少影响受灾民众的需求满足，投入过多，虽然可以最大化满足受灾民众的物资需求，但是可能会造成资源浪费，并且失去经济效益和社会效益的平衡，因此在实际决策中需要根据综合需求来获取两者间的平衡。文中列出了其中一种可行的物资预储方案，见表3。五种不同的物资是在发生了需要启动Ⅰ级响应的地震场景下进行计算得到的各层级不同储备库中的分布情况，并且通过计算得知模块物资接近所设定的比例关系，通过实验结果可知本模型可以合理有效地用于应急物资储备体系的优化。

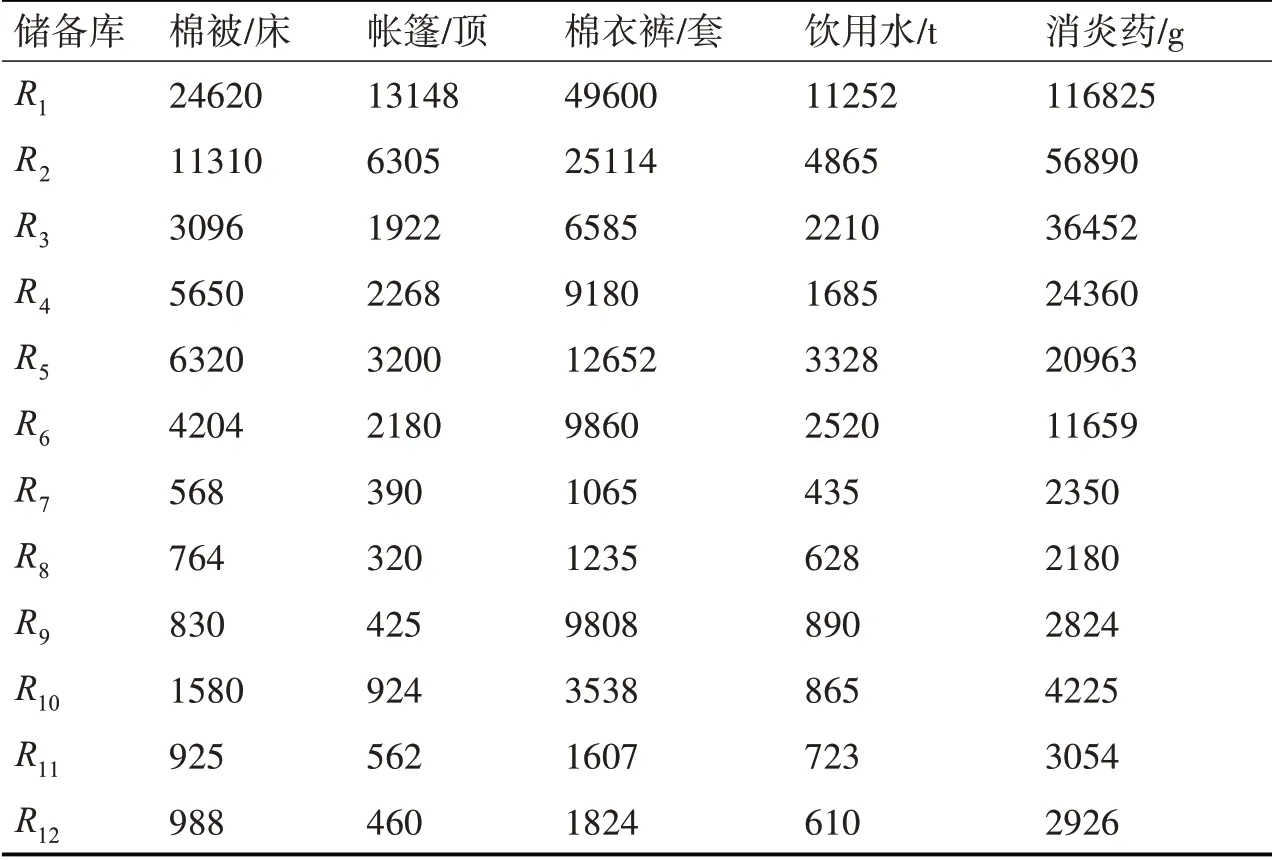
表3 各类物资在储备库中的分布情况

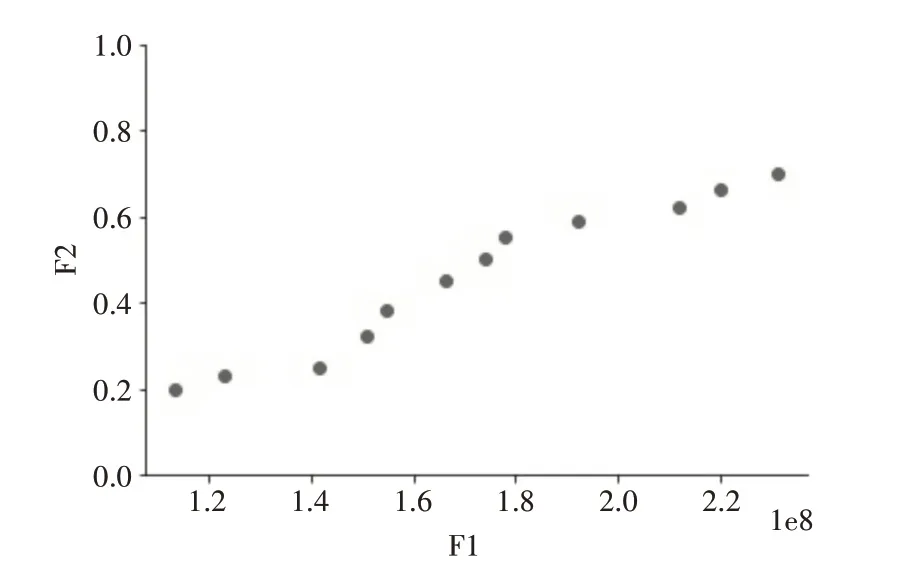
图2 迭代200次后的Pareto最优

5 结语

本文参考刘宗熹提出的储备指数［17］来确定各集散点的物资需求偏好量，通过三角模糊数描述对灾后需求点的物资需求供应的匹配程度，从而构建灾后物资供应效果的满足率目标，有效地避免了因需求不确定对物资储备决策造成的困难，同时也兼顾了民众效益。为了更好地达到灾后物资救援的效果，基于物资模块化的概念，将相互辅助搭配使用可以更好发效果的物资进行模块化处理，协调数量上的比例关系，并且通过到达时间的限制，从而提高救援的应急响应能力。另外，研究中考虑到不同层级储备库具有不同的储备能力，并且结合各层级储备库所需的不同成本来最小化储备体系的总成本，最后采用添加扰动策略的NSGA-II 算法求解各物资在储备中的合理储备量。

目前，本文提出的储备决策模型并未考虑储备库和集散中心的选址问题，因此，在未来的研究中，可以综合考虑选址和物资储备两阶段问题模型，另外在实际问题处理中，决策者可以根据不同储备区的实际需求分别赋予两个目标函数相应的权重，从而更加合理地储备物资。