基于形态学和小波包变换的红外弱小目标检测*

冯 洋

（渭南师范学院物理与电气工程学院 渭南 714000）

1 引言

红外告警系统中红外弱小目标检测一直是图像处理领域的热门研究，由于红外目标成像距离远，背景复杂及杂波干扰使得获取的图像信噪比较低，对目标的检测有一定的难度。数学形态学中的Top-hat变换和频域处理领域的小波变换被认为是该领域行之有效的两种方法［1～2］。但Top-hat 变换由于受结构元素的影响使得其对目标的检测能力有限，特别是在强起伏背景下，Top-hat变换有可能会降低图像的信噪比，使得目标无法检测［6～7］。小波变换是在频域范围对图像进行多尺度分解，然后选取合适的分解系数对图像进行重构达到背景抑制效果［8～9］。为了达到理想的效果，国内外学者做了大量的工作进行系数的优化，但由于在红外弱小目标图像中目标、杂波和背景边缘等干扰都表现为高频特性，所以单一系数角度上优化也不能很好地抑制背景中除目标外的高频特性，因而取得的效果有限［10～11］。

本文提出了一种将Top-hat变换和小波包变换相结合的处理方法，该方法首先利用Top-hat 算子选取合适的结构元素对原始图像进行平滑处理，平滑掉大部分背景区域，然后利用小波包变换特点对图像进行多尺度分解，小波包变换能够在高频子带进行更详细的分解，针对目标特点选取高频频带中能量分布居中的频带节点系数对图像进行重构完成目标背景第二次抑制，最后精确的检测出目标。该方法通过与经典Top-hat变换和小波变换进行性能评估，证明了本文方法的有效性。

2 形态学Top-hat滤波的背景平滑

Top-hat 变换是灰度形态学的一种处理方法。它通过采用与目标形状相似的结构元素去度量和提取图像中的目标，去除不相干的杂波和背景，以达到提取和识别目标的目的。

Top-hat滤波变换可以记为

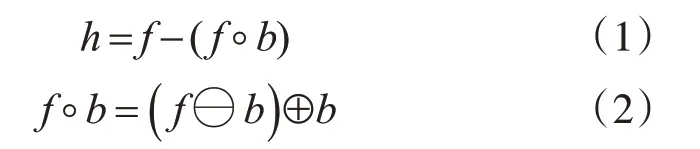
该变换是用原始图像减去形态学开运算后的图像。开运算通过采用合适结构元素对图像进行先腐蚀后膨胀的运算，能够滤掉大部分小于结构元素的目标和杂波，估算出大面积背景区域。因而通过用原始图像减去开运算后的背景估计就可以得到背景抑制后图像。

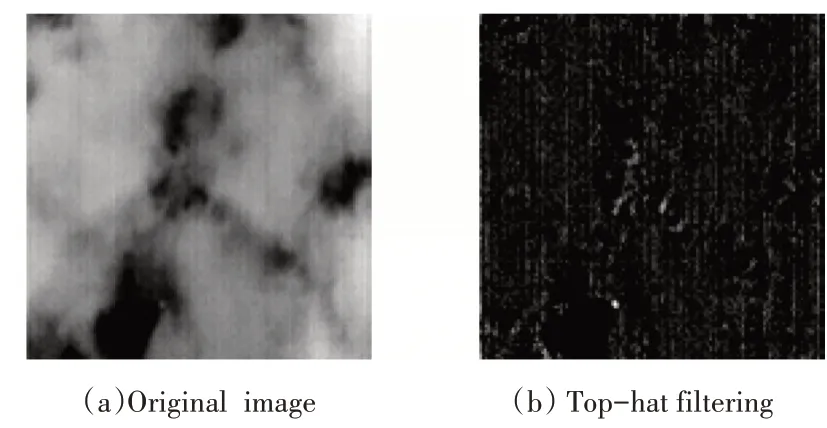
图1 Top-hat变换结果

经Top-hat 变换能够滤掉大部分的低频背景，但对于目标和杂波以及强起伏背景的轮廓边缘等依然存在，对后续目标的分割依然有难度，所以Top-hat 变换适合于信噪比高，背景比较平滑的红外弱小目标检测，对强起伏背景还要再一次地对背景轮廓和杂波进行抑制。

3 红外图像小波包变换

针对Top-hat变换后得到的背景抑制图像再一次利用小波包变换进行处理。由于小波包变换能够对高频子带进行更详细的分解，因而对目标、杂波以及背景的边缘轮廓能够实现多尺度的分解，可以获得精确的目标信息。

3.1 小波包变换［12～13］

在多分辨分析中，可以把L2(R)分解为不同的尺度下所有闭子空间Wj的正交和，即L2(R)=⊕Wj，j∈Z。Wj为小波函数Ψ(t)的小波子空间。如果将Wj以2 的幂次进行频带的细分，就可以实现信号的多尺度分析。由多分辨性质可知，尺度函数φ(t)和小波基函数ψ(t)满足双尺度方程：

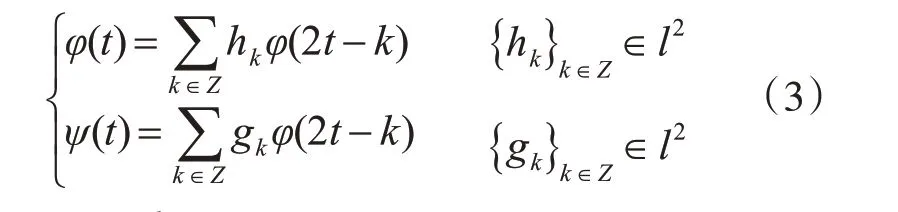
其中，gk=(-1)kh1-k，即两系数具有正交关系。

对于小波包变换是将尺度空间Vj和小波子空间Wj统一用子空间表示，令

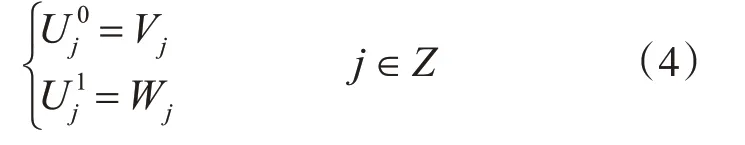
则L2(R)的正交分解可表示为

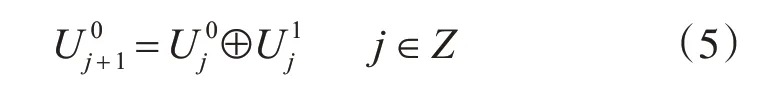
用u0(t)表示多分辨的尺度函数φ(t)，u1(t)表示小波基函数ψ(t)，则同意

则{un(t)，n∈Z}是由φ(t)确定的正交小波包，则un(t)递归定义为

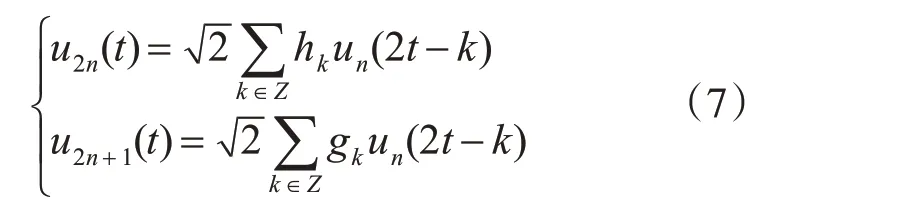
因此作迭代分解则有

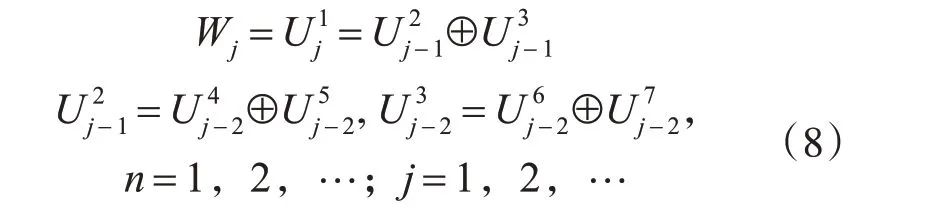
所以小波包可以对Wj进一步分解，将频谱窗口进一步分割变细，实现了比小波更加精细的分解方法，具有更好的时频特性。小波包变换将图像高频部分划分的更细，能够更好地表示大量细节信息，如图像中的边缘、纹理、杂波等。

3.2 红外图像小波包分解与重构

3.2.1 红外图像小波包分解

对Top-hat 变换后的图像进行了2 层小波包分解，如图2 所示。图2（a）为小波包分解的树形图，图上的左图标识了小波包分解的层数以及每层的节点数。每一层的第一个节点为低频节点系数，代表了图像灰度起伏不大的背景信息，后续节点为高频系数，重构为目标和杂波以及强起伏背景的轮廓边缘等高频分量。图2（b）为选取（0，0）节点重构的小波包频带分量图，通过选取不同的节点重构可以实现不同分量的选择。所以利用小波包变换进行背景抑制，就是利用小波包系数中的高频频带系数进行图像重构，但为了使目标分量更加的突出，可以根据被分析图像的特征，自适应地选择与之相关的高频频带系数进行重构，得到更好的背景抑制图像。

图2 红外图像小波包分解

3.2.2 红外图像小波包重构

对红外弱小目标图像的再一次背景抑制可以采用高频频带节点系数进行重构达到目的，选取高频节点系数的时候同时也要考虑噪声或起伏背景轮廓等对图像造成的扰动。假设对Top-hat变换后目标图像进行2 层小波包分解，则在第二层可将原始图像的能量分解到16 个正交频带上，对第j个频段的能量定义为某频段内的小波包变换系数的平方和［14～15］。

即：

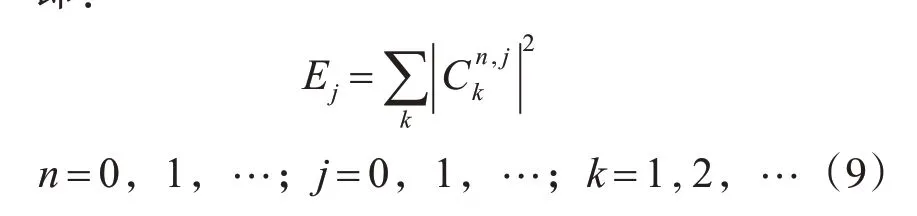
n 为小波分解的层数，j 为第n 层小波分解节点个数，Cn，jk为小波分解系数，k 为第j 个节点分解系数的个数。则图像高频信息的能量统计直方图如图3所示。

经仿真测试，红外弱小目标的信息的频带主要集中在高频频带能量居中的部分，如图3中的2、4、6、9、11、12 等节点，对能量大的高频节点成分，它不仅仅是对红外目标的贡献大，同时也会增大起伏轮廓背景的能量，对这些节点的选取不利于后续目标的分割。对于信息能量比较小的节点又对目标贡献不大，只会导致更多细小杂波的引入，同样也不利于后续的目标分割。因而选取合适的高频节点系数完成图像的重构即可以保证目标能量损失不大，也能达到很好的背景抑制效果［16］。

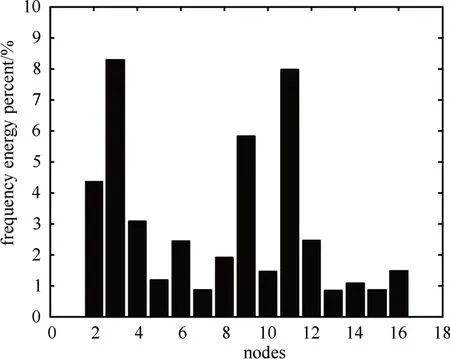
图3 频带能量统计直方图

4 实验结果与分析

文章选取强起伏云天背景下的红外弱小目标图像序列进行仿真验证，图片大小为128×128，目标大小约为3×3 左右，256 灰度级。仿真实验分别采用Top-hat变换和小波变换以及本文提出方法进行背景抑制，Top-hat 变换采用结构元素为2 的圆盘结构进行变换，小波分解和小波包分解都采用“db2”小波进行，小波分解采用软阈值处理系数。小波包分解重构系数采用高频频带能量总和的5%～15%范围内的频带节点系数进行重构。

首先我们对真实序列图像的第18帧和第32帧进行三种方法的背景抑制，处理的结果如图4 和图5 所示，其中（a）为原始图像，（b）为Top-hat 变换处理结果，（c）为小波软阈值处理的结果，（d）为本文处理算法效果。

图4 实验结果一

图5 实验结果一

文章选取的两幅图片都为强起伏云天背景，特别是云层边缘的干扰比较明显，所选目标都处于云层边缘，与目标周围背景对比度不大，并且强度较弱。从两幅图片采用不同方法处理结果可以看出，强起伏背景下Top-hat变换针对这种红外点源目标还是有一定的效果，但任然保留了部分背景；小波分析软阈值直接处理的结果不理想，保留目标信息的同时保留了大量的背景轮廓信息，后续目标分割难实现；本文提出的方法在实验效果上要优于前两种算法，从图（d）上可以看出背景几乎都被平滑掉了，保留的目标信息明确，目标强度虽有所损失但远高于背景灰度值。图6和图7为原始图像和本文所提方法处理后的三维灰度图。

图6 灰度三维图

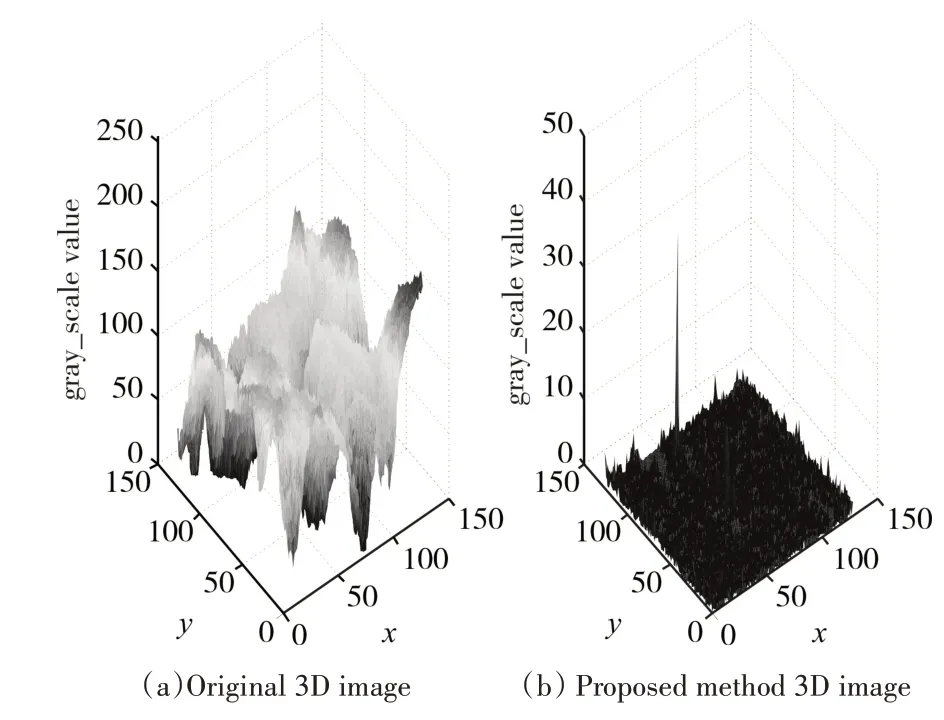
图7 灰度三维图

从图6和图7灰度三维视图可以看出本文采用的方法能够很好地抑制强起伏的云天背景，目标保留信息能量大，在后续采用简单的目标分割方法就可以很容易提取出目标。本文对两幅图像目标分割后提取到的目标中心像素点坐标分别为（102，32）和（108，51），与实际目标位置相符。

5 结语

文章针对强起伏背景下红外弱小目标的检测问题，采用Top-hat 变换和小波包变换相结合的方法进行目标检测。该方法首先通过Top-hat变换进行初次背景抑制，平滑掉大部分背景，在此基础上采用小波包变换获取高频信息频带能量进行重构实现背景的第二次抑制。通过真实红外序列图像模拟仿真验证，该算法能够很好地抑制强起伏背景，提高目标与背景的对比度，并与Top-hat 变换、小波变换滤波进行比较，该算法在一定环境下背景抑制效果要优于以上两种算法，因而该方法具有一定的理论指导意义。