改进的蚁群算法在定制公交路径规划中的应用*

王 奔 张 森 刘月锟 武 曲 刘秀燕

（青岛理工大学信息与控制工程学院 青岛 266525）

1 引言

近年来市民出行需求趋向多元化，公交服务模式单一问题日益凸显，公共交通多元化已经成为必然趋势［1］。定制公交旨在解决高峰期居民上下班和传统公交服务质量差等问题。为客户群规划路线，一站直达，能够很好地弥补传统公交在灵活性、舒适性和便捷性等方面的不足。早期，国内外在定制公交研究上重点集中在运营方式、监管政策的制定［2］。而定制公交的线路规划作为公交运营发展的重要环节和核心问题，对提高定制公交的实践价值具有重要作用［3］。

对于定制公交路径规划的研究应用，在站点的选址与布局方面，文献［4］将选址布局抽象为聚类问题，通过K-means 算法求得站点分布，并根据运营成本最低原则设计公交路径。文献［5］将成本因素考虑在内，依托现有公交站点进行路线规划，提升了公交站点利用率。在线网优化方面，文献［6］将乘客抵达时间和运营成本作为优化目标，并以直接连接能力和换乘次数为约束条件，构建线路优化模型。文献［7］将快速轨道交通系统中的“一路一线”思想融入公交路网规划，设计了一种“逐条布设，优化成网”和“一路一线”的线网优化方法。文献［8］将时间、上座率、路径长度三大指标作为约束，建立以最大运营效益和最大服务覆盖率双目标线路优化模型，并给出了求解的改进蚁群算法。文献［9］从公司运营成本和乘客利益出发，建立了可变线路式公交调度模型，并采用遗传算法求解。文献［10］以经营费用、乘客的出行时间为优化目标，车辆人数限制、乘客上下车时间窗、不确定乘客等车时间为约束，建立了多目标鲁棒优化模型并采用改进的NSGA-Ⅱ算法进行求解。在线路规划求解算法方面，传统的路径规划算法有Dijkstra算法［11］、A*算法［12］等。随着智能仿生学算法的不断发展，蚁群算法［13］、粒子群算法［14］等智能算法被应用到路径规划上。蚁群算法最早用来求解旅行商问题。现主要应用于车辆运输调度、机器人路径规划等问题。蚂蚁在觅食过程中分泌信息素，蚁群通过信息素进行交流，利用群体智能逐渐找到最优路线。但随着不同路径信息素的差异增大，存在易陷入局部最优解，前期随机性较大，导致收敛速度慢等问题。文献［15］提出首尾双向搜索思想来提高算法的全局搜索能力。文献［16］提出变异因子策略和狼群分配策略，改进转移公式，提高了蚁群寻优效率。文献［17］改变了按照经验设置参数的惯用模式，用粒子群算法对参数进行优化，节省了时间，寻优结果得到改善。

综上所述，国内外线路优化问题主要集中在公交选址布局与线路优化模型的建立层面，仅有少量关于定制公交路径求解算法及其优化问题的研究。在路径规划算法中，蚁群算法求解精确度高、收敛速度快、寻优能力强，能很好地和定制公交路径规划问题结合起来，但存在易陷入局部解、收敛速度慢、参数设定优劣直接影响最优解等缺点。因此，本文提出一种改进的蚁群算法综合路径规划方案，通过改进双向搜索策略，加入狼群分配策略，从而增强算法的全局搜索能力，提升收敛效率。另外，以定制公交运营成本和乘客上座率为优化目标，公交容量限度、乘客预定上车时间为约束条件构建综合评估模型，作为路网优化的评价标准。为合理设定参数，本文使用收敛能力强的粒子群算法对参数调优。最后，通过实验仿真验证了算法的有效性。

2 环境建模

本文针对定制公交所处的工作环境进行二维空间建模。由于公交行驶路径是点对点的交互模式，因此可将公交路线抽象成多个点连接而成的复杂网络，采用可视图法进行建模。

如图1 所示，本文定制公交站点布局依托实际公交站点，将路网结构抽象为二维网格。用节点表示公交站点，节点间连线表示路段。另外，每一个站点根据所在的位置编号为xij，并假设x11为始发站，x66为终点站。相邻站点之间距离用disij表示，各站点的预计乘车人数用peoij表示。从理论上讲，定制公交在行驶过程中会有很多方向，但考虑到环境模型的复杂性，本文设定公交车定向行驶过程中共有两个运动方向：U和L，定制公交每步只能移动到相邻的一个站点。

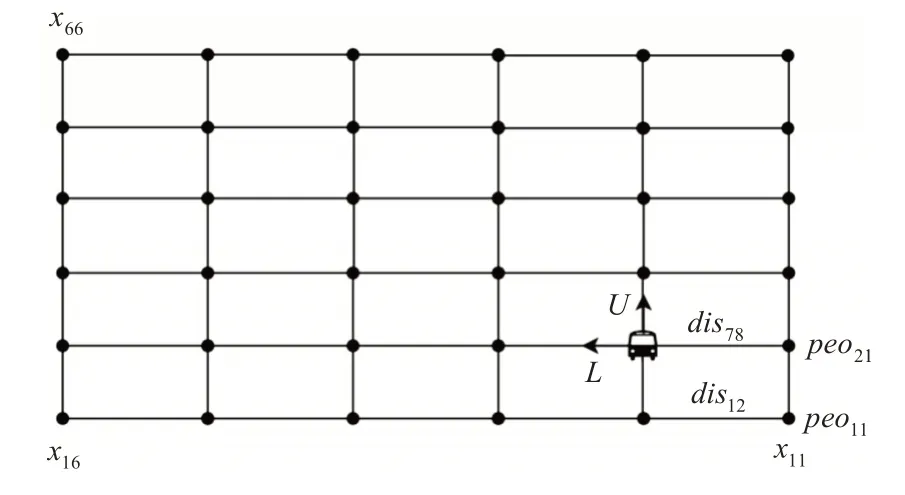
图1 定制公交路网模型

3 传统蚁群算法

传统蚁群算法应用在定制公交路径规划中的大致流程为：初始化、搜索路径、更新禁忌表和信息素［18］。首先初始化蚁群算法的参数，将蚂蚁放置在起点，根据移动规则，蚂蚁不断向前行走直至找到终点，并将移动的位置加入到禁忌表中。对于蚂蚁k从当前节点i选择节点j的转移概率是根据信息素浓度和启发式函数确定的，转移概率由式（1～2）确定。

为避免残留信息过多使得算法陷入局部最优，在蚂蚁循环一次之后，要对每条路径上的信息素按式（3～4）进行更新。

式（3～4）中，Q 为常量，表示信息素强度；ρ为信息素挥发系数，取值为0～1；m为蚂蚁数量；为蚂蚁k在路径（i，j）中留下的信息素；Lk为蚂蚁k 在本次循环中走过的路径总长度。

4 改进的蚁群算法

4.1 改进的双向路径搜索策略

在传统的蚁群算法中，所有蚂蚁全部从起始点向目标搜索，为此文献［15］将所有蚂蚁平均分为两组：A 组、B 组，A 组由起始点向终点搜索，B 组由终点向起始点搜索。两组的蚂蚁相遇时，将两者的路径连接得到一条搜索路径，提高了搜索效率，但是使得算法的全局搜索能力提升不足。因此，本文引入信息交流转移因子，使相遇的两只蚂蚁可以选择走彼此已走过的路线，也可以继续随机搜索。

式（5）表示两只蚂蚁相遇的条件，其中meetij为蚂蚁i与蚂蚁j是否相遇。式（6）表示两只蚂蚁是否选择彼此路径的判断条件，1 为选择，0 则不选择；rand为随机值，表示信息交流转移概率；ps为常数，表示信息交流转移因子，如果rand大于此常数表示两蚂蚁选择彼此的路径而进行转移。

4.2 基于狼群分配的信息素更新策略

随着迭代次数的增加，各路径信息素会存在堆积或挥发至0 的情况。本文参照文献［16］使用狼群分配策略，依照“强者生存”的更新机制进行分配［19］。在迭代过程中，参照狼群算法中的“论功行赏”分配策略，对每代效果好的路径进行奖赏，对效果差的路径进行惩罚。加入狼群分配策略后，信息素的更新规则如式（7～9）所示。

4.3 综合评估模型

启发式函数ηij表示蚂蚁由节点i 转移至节点j的期望程度，传统蚁群算法中的定义如式（2）。而对于定制公交路径规划问题来说，衡量一条路线的标准不仅仅是参考路线的长度，应额外考虑公交车在行驶过程中载客的数量以及消耗的成本等因素。因此本文以公交运营成本和乘客上座率作为优化目标，车辆核载人数、乘客预定时间为约束条件建立综合评估模型，模型的解充分反映了由节点i转移至节点j的综合消耗，并以此来改进启发式函数。

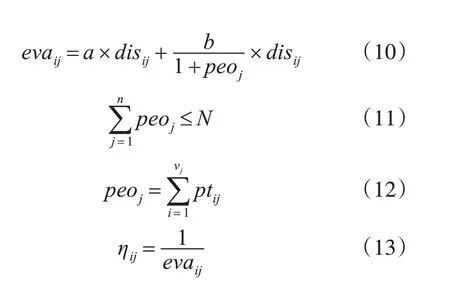
式（10～12）表示综合评估模型，式（13）表示改进的启发式函数，其中evaij为节点i 转移至节点j 的综合消耗；peoj为下一站j的实际乘车人数；N为定制公交核载人数，n 为所经站点总数；Vj 表示站点j 的预计乘车人数；ptji为j站点中第i个人预定上车时间，pt∈[T，T+X]，其中T 表示当前班次车辆发车时间，X 为不确定乘车等车时间；a、b 为调整参数，取值为0～1，当a取值为1、b取值为0时式（13）退化为式（2）。

4.4 基于改进粒子群的参数优化

蚁群算法中，参数取值有非常大的影响。为此利用粒子群算法较强全局收敛的能力，对蚁群算法中的重要参数进行优化，通过重复调用蚁群算法在多次迭代过程中完成算法的参数优化，在此过程中根据式（15）作为评判参数优劣的标准。

式（14）中，i、j 为路径Mt中的相连节点，evaij的定义如式（10）。式（15）中，fit 为适应度函数值；syn(Mt)由式（14）计算得来；ite 为算法得出最优解时的最少迭代次数；λ和μ为取值0～1 的常数，表示适应度函数和最少迭代次数的权重系数。

首先初始化粒子群体，将每个粒子搜索到的参数带入改进后的蚁群算法中，根据式（15）计算出粒子的适应度，最后选择最优的参数。在搜索过程中，每个粒子的移动速度和位置按式（16～17）进行变化。

式（16～17）中，c1和c2为学习因子；ω为惯性因子；r1和r2是取值0～1 的随机数，用于调整粒子的搜索空间；pbest 和gbest 分别为个体最优值和群体最优值。

由于传统的粒子群算法极易陷入局部最优问题，常常会对其参数进行改进［20］，采用动态改变惯性因子的方法来跳出局部最优。若使用递减函数来改变惯性因子，当算法陷入局部最优时，惯性因子也会变得比较小。因此使用一个函数来使其陷入局部最优时的惯性因子变得比较大，这样算法可以继续搜索，从而增强全局搜索能力。

通过以上分析可知，这样的函数应先递增后递减，在陷入局部最优的点附近达到最大值。设定一个二次函数来改变惯性因子的大小，如式（18）。

式（18）中，k 为迭代次数。a、b 和c 是常数，通过待定系数法来求出它们的取值。

5 结果与分析

为验证改进算法的有效性，采用Matlab进行仿真实验。构建多个不同规模的路网模型，分别从最短路径规划、最优综合指标路径规划两方面来验证改进后算法的优越性。

5.1 最短路径规划

由于定制公交路径规划涉及到路径长度、乘车人数等因素，若直接采用综合评估函数很难直观体现改进算法在常规路径规划上的优势，因此，本文先将路径长度作为唯一指标进行验证仿真。为充分体现改进算法的性能，选用规模为50×50 的路网结构进行仿真。

首先，传统蚁群算法、采用双向搜索策略的文献［15］和本文算法各自得出的路径如图2 所示，每代最优路径长度和迭代次数对比如图3 所示。最终结果表明，本文算法的全局搜索能力有了明显提升，得出的路径更短，但收敛能力提升不足。

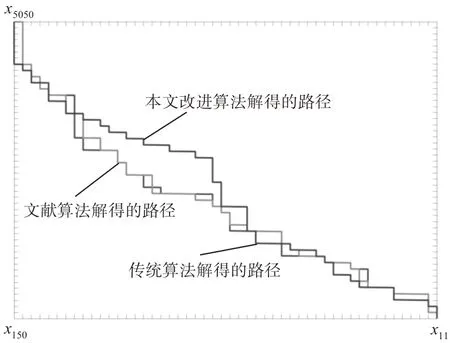
图2 三个算法最优路径

图3 三个算法指标比较

传统蚁群算法得到的最优路径长度为302.4。文献［15］对应的路径长度为290.94，相比之下，文献［15］在全局搜索能力方面有所提升。而本文算法进一步增强了算法的全局搜索能力，找出了长度为285.88的最优路径。

此外，传统蚁群算法在迭代41 次后收敛，文献［15］所用算法在迭代29 次后收敛，而本文算法在迭代36 次后收敛。分析可知，文献［15］和本文算法相较传统算法在收敛速度方面有所提升，但本文算法在收敛速度上弱于文献［15］。

5.2 综合模型路径规划

由上述结论可知，本文算法相比于传统蚁群算法有了明显提升。而在定制公交路径规划问题中，路径长度不再是唯一指标，还需考虑到上座率。在两者之间达到平衡点，才能获得利润最大值。

为了验证本文算法综合性能的优越性，将综合评估函数作为适应度函数的指标进行验证仿真。如式（14）所示，综合评分越低，代表该路径越好。为了更直观证明算法的有效性，选用6×6 的简易路网结构。

首先，传统蚁群算法和本文算法所求路径如图4 所示。各算法综合得分对比图如图5 所示。另外，将两种算法的各类指标列入表1 中。由表1 可知，本文算法所求路径在长度上稍长于传统算法，但是乘车人数明显增多，综合评分也低于传统算法，故而说明了本文算法以综合评分为标准，很好地兼顾了行驶距离和乘车人数，综合优化性能相较传统算法得到提升。

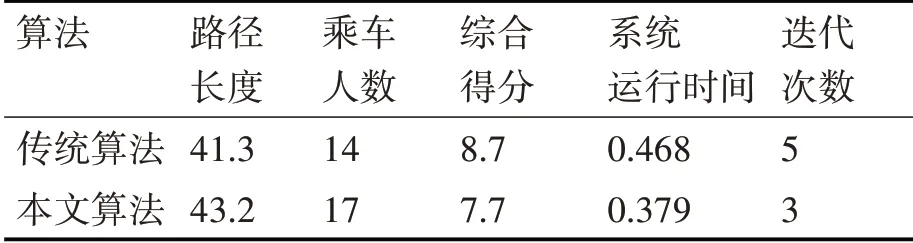
表1 传统与本文算法指标对比

图4 传统与改进算法解得的路径

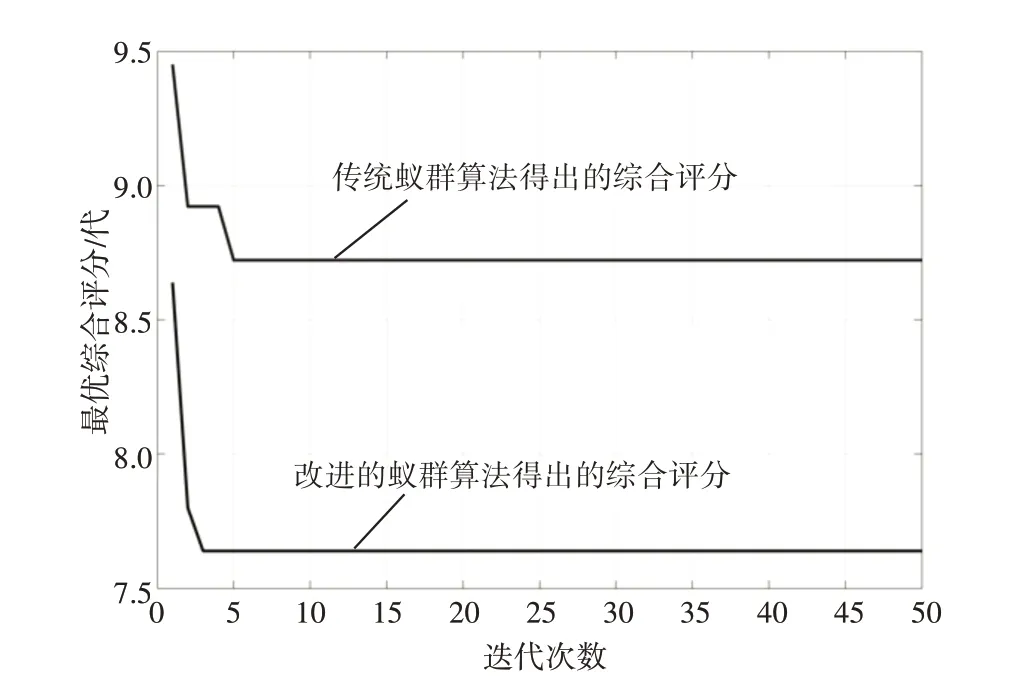
图5 传统与本文算法综合得分

分析可知，6×6 的路网结构比较简单，两种算法皆能对所有路径进行遍历。传统算法将行驶距离作为唯一指标，求得该路网模型的最短路径。而本文算法综合考量行驶距离和乘车人数，求得该路网模型在两指标下的最优路径。相比之下，本文算法更加符合公司利益，达到了便捷乘车和经济效益的统一。

6 结语

本文研究了面向定制公交路径规划问题的蚁群算法，分析了传统蚁群算法解决定制公交问题的优缺点，并提出了一种改进的蚁群算法。本文首先引入改进的双向搜索策略，扩大算法前期搜索范围；引入狼群分配策略改进信息素更新原则，进一步增强了全局搜索能力；另外，建立了综合评估模型，既降低了运营成本，又增加了乘客上座率；最后，引入改进的粒子群算法进行优化，将综合指标带入适应度函数调校出最优参数。实验结果表明，改进后的算法在最短路径规划和综合指标路径规划方面有了显著提升，但是算法收敛速度有待加强。