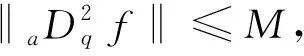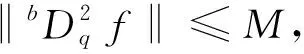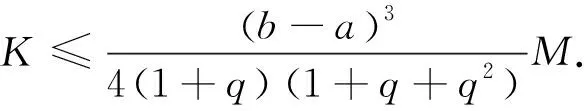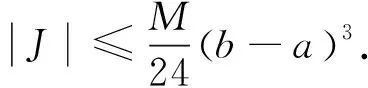二阶可微函数梯形不等式的几个量子模拟
2022-06-15时统业
时统业
(海军指挥学院,江苏 南京 211800)
0 引言
设f是[a,b]上的可微函数,且存在常数M,使得对任意x∈[a,b]有|f′(x)|≤M,则有下面Iyengar积分不等式[1]:
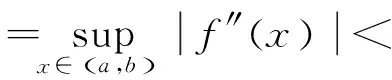
(1)
许多学者给出了式(1)的带有扰动的推广,也是在二阶导数有界也即|f″|≤M的情况下Iyengar不等式的推广.记
参考文献[3]建立了优于式(1)的不等式
(2)
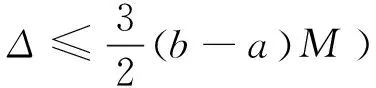
(3)
参考文献[5]还是用引入参数求最值的方法,建立了强于式(3)的如下不等式
参考文献[6]给出式(1)的另一个带有扰动的推广
(4)
其中
参考文献[7]通过引入参数求最值,用解析方法给出式(4)的新的证明.
关于Iyengar不等式更多的改进和推广,见参考文献[8].本文的目的是通过建立恒等式将式(1)推广到量子积分,还要仿照参考文献[7]证明不等式(4)的方法,将不等式(4)推广到量子积分.
1 基本概念和引理
在本节,介绍一下本文涉及的量子微积分的基本知识和证明本文主要结果所需的引理.
定义1[9-10]设f是[a,b]上的连续函数,则f在点x∈(a,b]处的q导数定义为
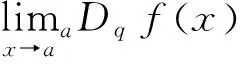
如果f在[a,b]上每个点处的q导数都存在,则称f是[a,b]上的q可微函数.
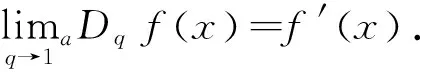
定义2[9-10]设f是[a,b]上的连续函数,t∈[a,b],则f在[a,t]上的q积分定义为
设c∈(a,t),则定义
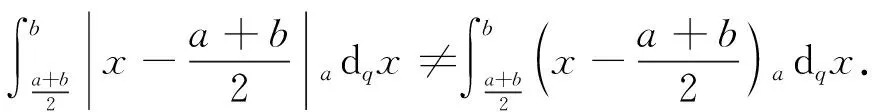
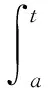
定义1和定义2分别是[0,b]上的q-Jackson导数和q-Jackson积分[11]的概念的推广.
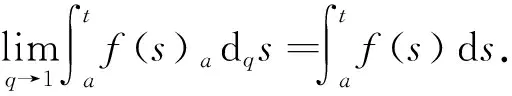
定义3[9]设f是[a,b]上的连续函数,对于任意x∈(a,b],称
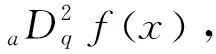
引理1[9-10]设f是[a,b]上的连续函数,则对于任意a≤c 引理2[9](q积分的分部积分公式) 设f,g在[a,b]上q可微,则有 另一方面,对应于q导数和q积分,参考文献[12]给出qb导数和qb积分的定义. 定义4[12]设f是[a,b]上的连续函数,则f在点x∈[a,b)处的qb导数定义为 如果f在[a,b]上每个点处的qb导数都存在,则称f是[a,b]上的qb可微函数. 定义5 设f是[a,b]上的连续函数,对于任意x∈[a,b),称 定义6[12]设f是[a,b]上的连续函数,t∈[a,b],则f在[t,b]上的qb积分定义为 设c∈(t,b),则定义 一般是不成立的. 对于[a,b]上qb可微函数f,g,有qb积分的分部积分公式 引理3 设f在[a,b]上q可微,则有 (5) 证明 利用q积分的分部积分法(引理2)得 引理4 设f在[a,b]上qb可微,则有 (6) 证明 利用qb分部积分法可证.证明类似于引理3的证明,这里略去过程. 利用q分部积分法和qb分部积分法还可以证明下面的引理5和引理6,限于篇幅,这里省略过程. 引理5 设f在[a,b]上q可微,则有 引理6 设f在[a,b]上qb可微,则有 引理7 设f在[a,b]上q可微,则对任意x∈(a,b]有 证明 利用引理1有 引理8 设f在[a,b]上qb可微,则对任意x∈[a,b)有 证明 与定理7的证明类似,这里略去过程. 有关q积分和qb积分不等式的结果还可参阅文献[13-17]. 定理1 设f在[a,b]上q可微和qb可微,且 则有 (7) 其中 证明 将引理3中的式(5)与引理4中的式(6)相加得 根据q积分的定义得 (9) 类似可得 (10) 综合式(8)至式(10),则式(7)得证. 证明 由引理5有 证明 由引理6有 定理4 设f在[a,b]上q可微和qb可微,且 则有 (11) 其中 证明 利用引理7和引理8有 故式(11)成立. 定理5 设f在[a,b]上q可微和qb可微,且 (12) 其中 证明 由引理7和引理8有 τ1-τ2=σ(qk-μ), 其中 在引理7中取x=b,在引理8中取x=a,得 (13) (14) 由假设有σ>0。又由式(14)知μ≥0。又由式(13)有 故μ∈[0,1].当μ=0时,令K=∞.当μ=1时,令K=0.当μ∈(0,1)时,令K=[logqμ],则当0≤k≤K时,qk≥μ,τ1≥τ2;当k≥K+1时,qk<μ,τ1≤τ2. (15) 其中 由logqμ-1 所以有 (16) (17) 其中 T=2[f(b)-f(a)]-(b-a)[adqf(a)+bDqf(b)], (18) 其中 经简单计算可得 利用这些结果得 U1=(1-q)T+qθ2(b-a)[adqf(a)-bDqf(b)] (19) (20) 综合式(15)、式(16)、式(18)至式(20),得 (21) 对(-f)应用已证结果,得 (22) 综合式(21)和式(22),则式(12)得证. 定理6 设条件同定理5,则有 (23) 其中θ2同定理5. 证明 从qb积分的定义出发,利用引理7和引理8可证.证明类似于定理5,故略去过程. 注2 定理5和定理6是不等式(4)在量子积分中的推广,令q→1,则由式(12)和式(23)得到式(4).
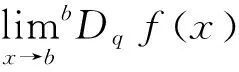
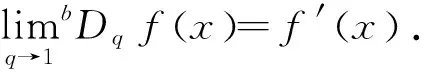

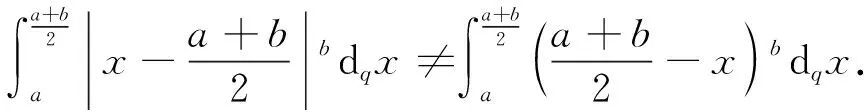
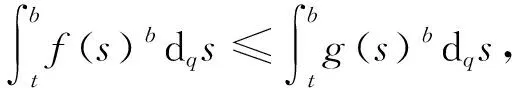
2 主要结果