密拼叠合板拼缝区域有限元静力分析参数优选

曾 鑫 余润琪 王 伟 李泽深

(绍兴文理学院 土木工程学院，浙江 绍兴 312000)

0 引言

叠合板是在预制底板上现场浇筑一层混凝土而形成的一种叠合式钢筋混凝土楼板[1]，其具有脚手架和模板节省、整体性较好等优点，已广泛应用于混凝土装配式结构中.四边出筋叠合板(图1-a)存在一些影响其效率和质量的常见问题：工厂生产时需要根据伸出的钢筋(简称“胡子筋”)分布定制模具；运输时胡子筋的碰撞会影响其质量；现场浇筑现浇层时需额外支设后浇带模板.但是，密拼叠合板(图1-b)由于不存在“胡子筋”，不存在四面出筋叠合板的上述问题.

(a)普通叠合板的拼接(有后浇带) (b)密拼叠合板的拼接(无后浇带)

目前，针对密拼叠合板静力性能的研究已包括试验研究和有限元模拟研究.国外学者主要专注于叠合面的抗剪问题，以及叠合面的抗裂和挠度的计算等问题[2-3].章雪峰等[4-5]针对四边不出筋、板侧采用密拼连接的钢筋桁架叠合双向板进行了足尺加载试验和原位加载对比试验.结果发现：叠合板在竖向荷载作用下的各项受力特性均表现出较为明显的双向板特征；其能满足正常使用极限状态与承载能力极限状态的要求. 林彦等[6]对3块不同拼缝连接方式的密拼叠合板和1块后浇带式叠合板进行静力加载试验，发现加强拼缝钢筋可提高密拼叠合板的极限承载力.余泳涛等[7]对多个单缝密拼钢筋混凝土叠合板进行静力加载试验，发现单缝密拼叠合板易在拼缝处发生沿叠合面的撕裂破坏.叶献国等[8]利用ANSYS对若干试验板进行非线性数值模拟.有限元建模时：选用整体式建模方法；分别采用Solid65单元和Link8单元离散混凝土实体和钢筋.研究表明，仿真值与试验值吻合较好；增加拼缝处连接钢筋和提高拼缝处截面有效高度可以提高承载力.在对密拼叠合板进行数值模拟时，不同类型的实体单元被研究者所采用，主要有C3D8,C3D8I等，不同研究者建模时划分的网格尺寸也有不同[9-11].已有的研究无法横向比较不同单元类型和网格尺寸对计算精度的影响.

密拼叠合板静力问题数值模拟时，数值模拟结果和成本依赖于单元类型、网格尺寸及材料模型等建模参数的配置.目前，针对密拼叠合板的有限元数值模拟参数选择相关的研究成果较为匮乏.因此，本文选择与密拼叠合板具有“相似几何特征和关键部位相似力学响应特征”的线弹性半圆形坡口板为研究对象，首先以遍历的方式采用不同的单元类型、不同的网格尺度离散半圆形坡口板的坡口区域，接着逐序地完成静力仿真，最后通过局部的两个指标——仿真解与解析解的偏离程度，物理仿真时间仿真值精度——的对比，给出拼缝区域建模时“单元类型和网格尺度”的组合优化配置建议.

1 板模型的两种简化处理

在进行密拼叠合板拼缝区域“单元类型和网格尺度”的组合优化配置的研究前，需要处理两个问题.

第一，叠合层的建模问题.密拼叠合板的底板进行拼接时，相邻两块板间没有联结(图2).拼接完毕后底板作为支撑进行上层混凝土浇筑，底板和现浇层之间通过混凝土的粘结作用和桁架筋的锚固作用进行相互连接，从而保证服役过程中板的整体性.因此，对叠合板进行数值建模时，底板和现浇层可作为整体进行建模.

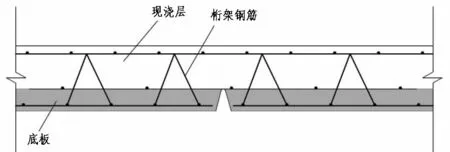
图2 密拼叠合板拼缝区域详图

第二，拼缝处的几何建模问题.两块底板(预制板)之间的拼接部位没有联结，因此将整块叠合板简化为一个底部带坡口的构件.真实工程中的叠合板的坡口几何形态类似于倒U形，并不是半圆形.倒U形坡口附近的应力集中效应和半圆形坡口附近的应力集中效应具有相似性——如最大正应力可采用同一个解析函数表示[12].因此，为了便于建模且不失一般性，采用半圆形坡口对拼缝处进行几何建模.

2 板的有限元建模

半圆形坡口板的有限元建模主要包括6个方面：几何信息、边界条件、加载点及其加载配置、单元类型和网格划分、材料本构模型及其参数、求解器配置.下面依序阐述这6个方面.

①几何信息.图3给出了半圆形坡口板的几何信息.其中，板长度l1=1 600 mm，描述加载点位置的l2=300 mm，板宽度b=300 mm，板厚度h=140 mm，半圆形坡口的半径r=5 mm.

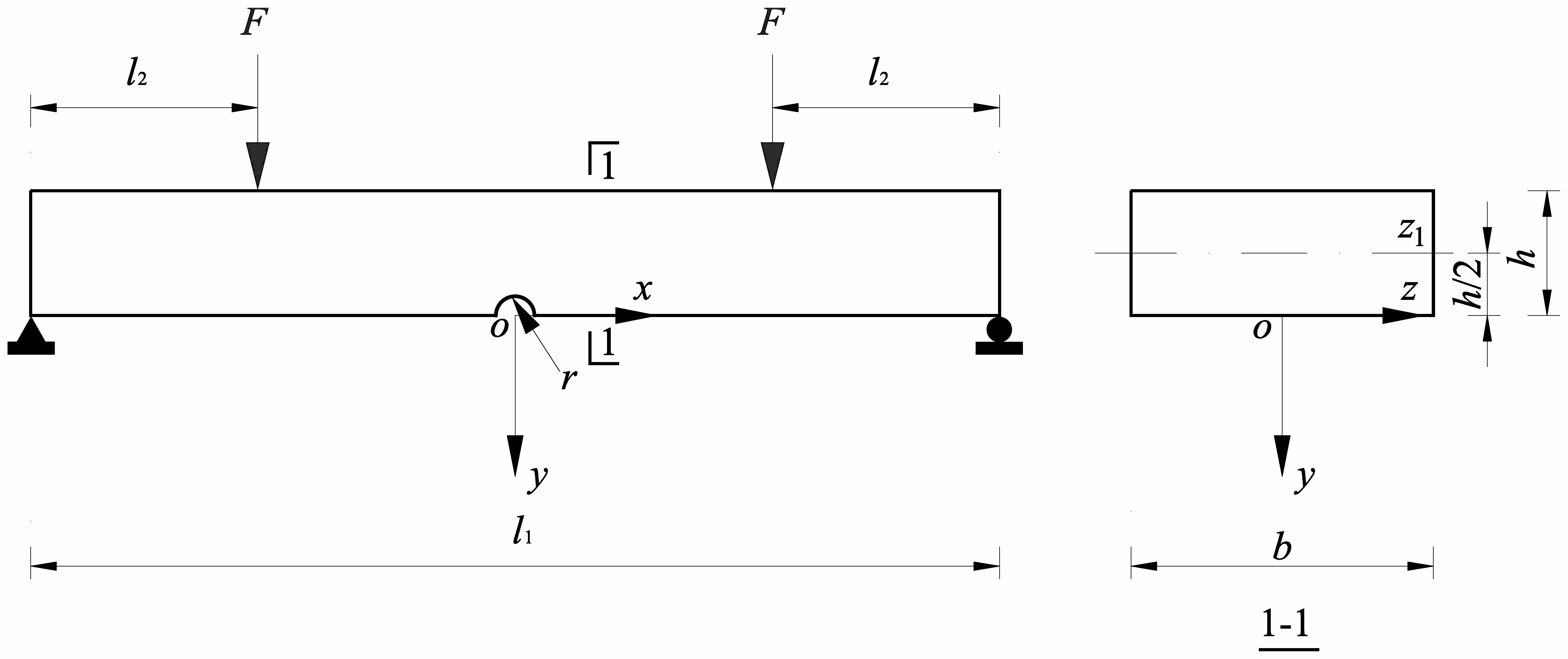
图3 半圆形坡口板

②边界条件.半圆形坡口板的左端为固定铰支座(上下左右平动同时被约束)，右端为可动铰支座(仅上下平动被约束)，详见图3.

③加载点及其加载配置.加载点的位置信息如图3所示，加载时采用力控制加载模式且两个加载点的力F相同.由材料力学知识易知，最大加载点力

(1)

式中，M为弯矩；σnom为名义应力，其可按

(2)

计算，其中的Wz1为正截面对中性轴z1的抵抗矩.对于图3所示的正截面，

(3)

对半圆形坡口板进行静力增量加载时，单个加载点的力F皆从初始时刻的0 N，随正值的各级增量，递增至结束时刻的Fmax；两个加载点的每级增量相同，每级增量的具体数值由ABAQUS内置相关程序控制.

④ 单元类型和网格划分.采用三维实体单元对密拼叠合板带模型进行离散，模型如图4所示.单元类型(A)和网格尺度(B)会影响计算精度和计算成本.为了能给出较为优化的组合(A，B)结果， 首先， 并行式地选用C3D8、 C3D8I、C3D20离散半圆形坡口板，其中C3D8为一般的3维8节点实体单元，C3D8I为3维8节点非协调实体单元，C3D20为一般的3维20节点实体单元；其次，并行式地选用四种网格尺度离散半圆形坡口板，该尺度可用数值i∈{50,25,12,6}指代(i的单位为mm).采用此四种尺度的半圆形坡口板的离散模型的正视图见图5.现以半圆形坡口板的一个算例C3D8-50进行半圆形坡口板编号的规则释义.此编号中，“-”前面的字符串C3D8表示该算例所选用的单元类型为C3D8；“-”后面的数值50表示网格划分尺度.半圆形坡口板的各算例的编号、单元类型、离散模型正视图见表1,对此表所列算例进行遍历式仿真后，易筛选出兼顾计算精度和计算成本的优化组合.

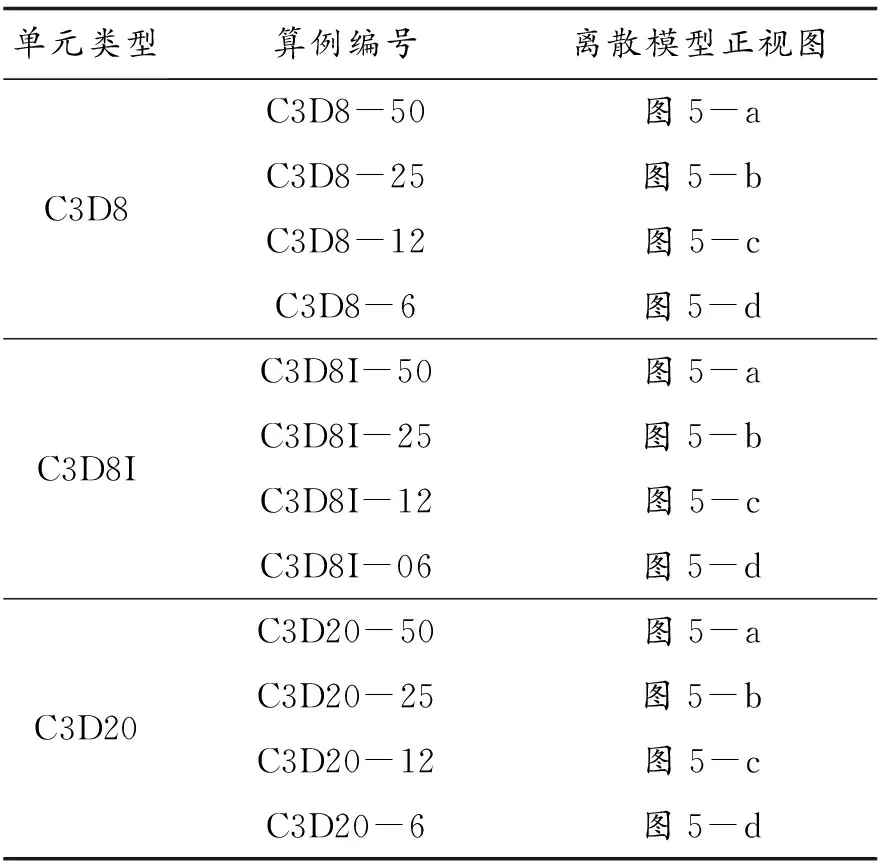
表1 半圆形坡口板的有限元模型信息清单

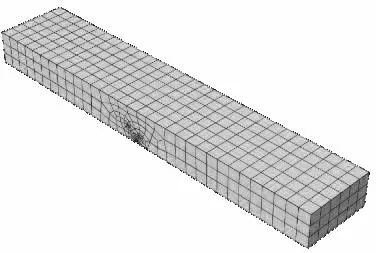
(a)离散模型的整体三视图

(a) C3D8-50/C3D8I-50/C3D20-50

⑤ 材料本构模型及其参数.确定单元中积分点的材料本构模型，且须使得本构模型及其参数取值，能正确地反映验证对象“半圆形坡口板”的主要力学特征——几何线性和线弹性.首先，为了保证线弹性，显然取线弹性本构模型

σ=Deε.

(4)

式中，σ为应力向量，ε为应变向量，De为材料弹性刚度矩阵.De的分量形式为

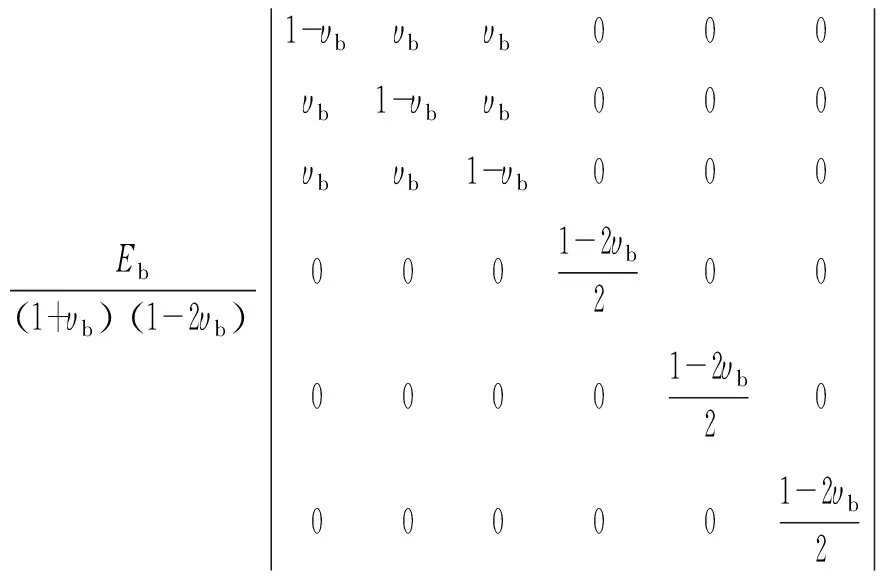
式中，Eb为弹性模量，υb为泊松比.因此，确定半圆形坡口板的本构模型时，仅需要确定Eb和υb的取值.其次为了保证小变形，取

⑥求解器配置.选用隐式求解器进行仿真，该求解器的配置参数见表2.

表2 隐式求解器参数配置

3 板坡口区域的解析/仿真解答

3.1 解析解答

参考文献[13]指出，几何线性和材料线弹性情形下，半圆形坡口板中坡口邻域的最大正应力

σmax=Ktσnom.

(5)

式中应力集中系数

(6)

其中的C1、C2、C3、C4为常系数，具体为

对于本文所分析的半圆形坡口板的几何信息(见图1)，即

r=5 mm,d=5 mm,h=140 mm，

(7)

可通过上述的表达式算得该板的坡口区域最大正应力处的状态量值为

σnom=15 MPa，Kt=2.73，

σmax=40.88 MPa.

(8)

依据文献[13]，能确定半圆形坡口板坡口邻域最大正应力的位置、方向和数值.该位置的空间坐标(x,y,z)=(0,5,0)；该方向平行于x坐标轴.另外，由文献[13]易判知，在z=0的xoy平面内距离圆心o(0,0)一定距离(如4r)处的x向正应力σ11趋于稳定.

图6 离散模型算例C3D8-25的应力等高线图

3.2 仿真解答

依据第3节所述的模型细节，对表1所列的半圆形坡口板的各算例进行模拟后，可得仿真结果.仿真时，取σnom=15 MPa，相应地由式(1)确定结束时刻的Fmax=49 000 N.表3列出了半圆形坡口板各算例的典型仿真结果.其中，σ11,s1为在z=0的xoy平面中，仿真所得坐标(x,y)=(0,-5)处的σ11；σ11,a=σmax=40.88 MPa为按式(5)求得的此处的解析解；σ11,s2为在z=0的xoy平面中，距离点(0,-20)最近的一个有限单元内积分点处的σ11；tr为相对仿真时间，由tr=t/t25算的，其中t为物理仿真时间，t25为C3D8I-25模型的物理仿真时间，其值为43 s.图6列出了算例C3D8-25的σ11应力等高线图.图7列出了所有算例在z=0的xoy平面中，区域D={(x,y)|-40≤x≤40,-40≤y≤0}的σ11应力等高线图.

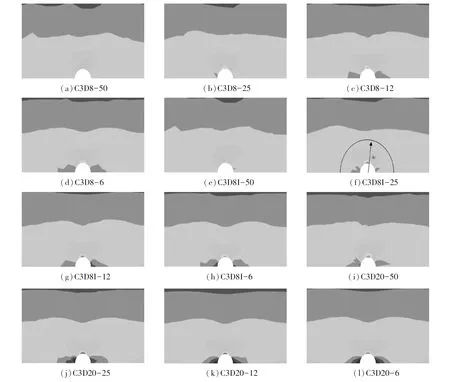
图7 各算例区域D的σ11应力等高线图

由上述仿真结果可得如下规律和结论.

① 无论采用哪种单元类型，在网格变小的情况下：t成指数规律增大；σ11,s1趋于稳定；σ11,s2≈10.5MPa；应力集中效应快速消散，在到圆心o距离大于4r时，可忽略此效应，详见图7，此数值解答规律和文献[13]的解析解答规律吻合.

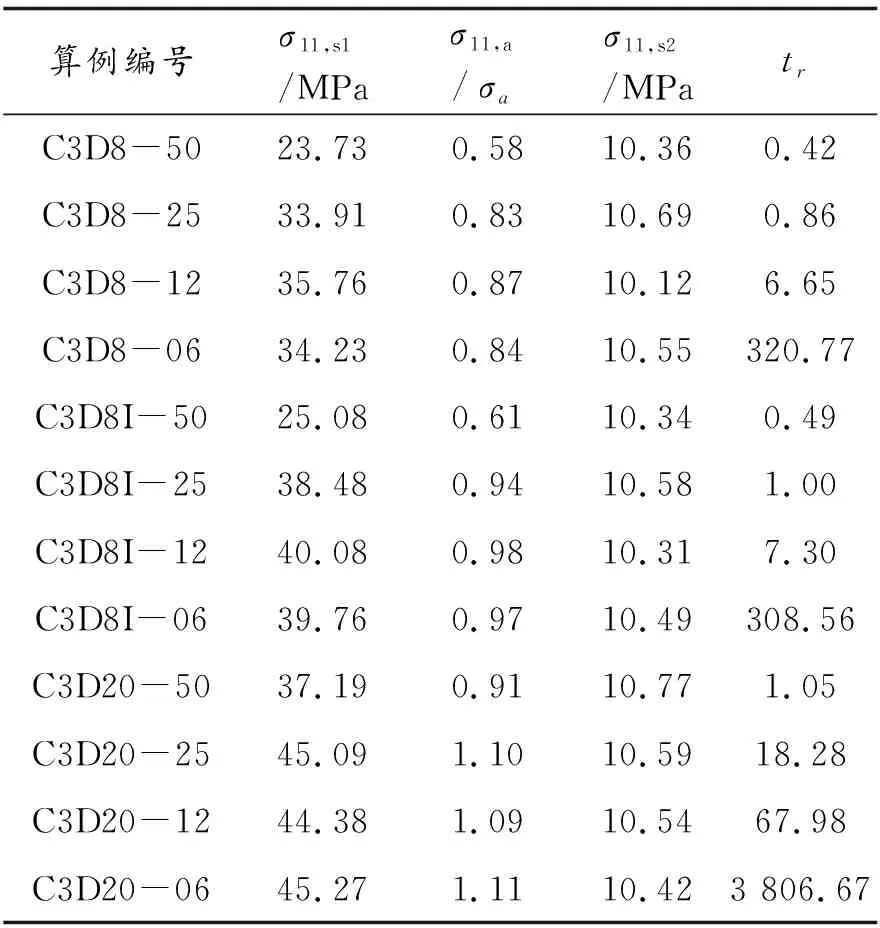
表3 半圆形坡口板仿真结果

依据上述两点，如单元类型取C3D8I，近似全局尺寸取25 mm，离散半圆形坡口板，相应的有限元仿真兼具结果的趋势正确性和计算的低成本性.

5 结论

针对密拼叠合板有限元分析时，拼缝区域的“单元类型和网格尺度”的组合优化配置进行研究.研究中：使用解析方法获取了拼缝区域最大正应力处的正应力量值，同时使用有限元隐式分析方法对采用不同网格尺寸和不同单元类型的线弹性拼缝板进行仿真，最终通过对比仿真解与解析解，给出了优化组合配置.具体研究结论如下：

(1)网格尺寸和单元类型对应力分析结果、物理仿真时间都有较大影响.在对应力集中部位进行应力分析时，需要优选合理的仿真参数.

(2)拼缝区域的网格尺寸越小，物理仿真时间越长，仿真精度随网格尺寸的变小而趋于收敛.

(3)单元的自由度越多，物理仿真时间越长.相同单元自由度的情况下，非协调模式单元的计算精度最高.

(4)综合本文仿真结果，当单元选用三维八节点非协调模式单元，网格尺寸选用25 mm时，可以仿真兼具结果的正确性和计算的低成本性.