某履带车时变力学系统模型建立与实验验证

张琼

（安徽三联学院 机械工程学院，安徽合肥 230000）

时变力学是研究具有随着时间变化内部参数动力学系统的一个学科分支，与经典的力学学科基于“恒定”假设的研究相比，时变力学改变了传统的力学研究角度，针对“时变”的特点，对动力学系统进行研究[3]。由于移动载荷与支撑结构的相互作用关系是随着时间变化的耦合关系，移动载荷作用在支撑结构上的系统是一类特殊的时变力学系统，在航空航天、兵器、机械、建筑、交通等工程领域中普遍存在，如车辆或者火车在桥梁上行驶、火炮后坐复进现象等。传统的时不变力学在火炮后坐复进现象中无法考虑后坐速度及加速度的快速变化，因此无法保证火炮射击的高精度，高准确性。近一个世纪以来，对移动载荷作用下支撑结构时变力学问题的理论研究一直是数学家、力学家和工程师共同关注的热点，研究者将时变系统的控制方程表达成具有时变系数的微分方程，与传统的结构动力学系统（定常系数微分方程）相比，其理论分析更为复杂[2]。

本课题以某火炮后坐时复进现象为基础提出关于变速移动载荷作用下时变力学问题的研究，不仅能够揭示移动载荷作用下悬臂梁的时变力学响应规律，同时能够为评价悬臂梁的动态性能提供依据，为悬臂梁结构的设计和制造提供重要的参照。

1 移动载荷时变力学模型的建立

由于火炮发射过程影响因素多而复杂，加之时变力学研究的局限性，要做到火炮时变力学的精确研究较为困难。因此本研究将火炮后坐系统中的炮身进行简化处理，构成移动质量-悬臂梁时变力学系统，即搭建起炮身在冲击载荷作用下大位移后坐的时变力学分析模型[1]。移动载荷作用下梁的动力学问题，在火炮发射系统中可以看成是火炮炮身大位移后坐的时变效应。

1.1 火炮结构及模型简化

火炮通常由炮身和炮架组成，构成炮身部分的是身管及其附件，炮身主要是保证弹丸的运动方向和稳定性。其中炮架的摇架部分对火炮射击过程至关重要，它不仅可以支承后坐，还是后座和复进的重要导向机构。炮身结构如图1 所示。

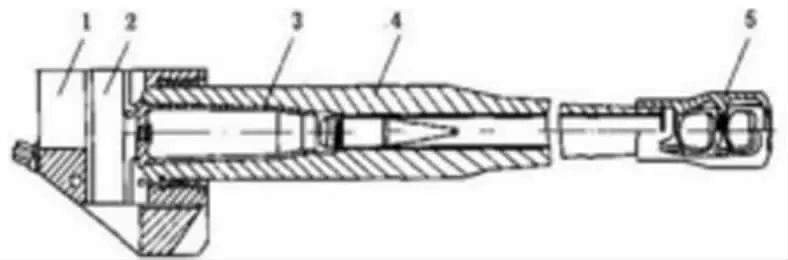
图1 炮身结构图

摇架是一个装在炮身下面的U形槽，反后坐装置位于框槽内，摇架的上表面沿着长度方向上有供火炮后坐部分使用的导槽。保证火炮在后坐、复进和行进过程中，炮身与摇架之间的接触为分布质量与支撑体之间的多方向的接触。因此，可将后坐过程中的摇架和炮身的结构抽象成如图2 所示的悬臂梁结构。

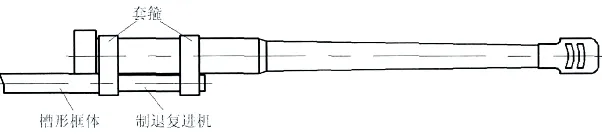
图2 摇架与炮身结构简化图

1.2 移动力学模型建立

在火炮炮身和摇架的结构模型中，后座过程炮身等效于集中质量的移动载荷；炮身与摇架简化为单个接触点；由于摇架外形复杂，可将摇架简化为等截面的悬臂梁；由于摇架上的耳轴室及高低机约束摇架的俯仰，即建立起悬臂梁的约束，经过以上简化处理并经过理想假设，建立起火炮后坐过程中集中质量-悬臂梁的时变力学模型。

图3 火炮后坐移动力学模型

2 时变力学实验验证

2.1 实验基础条件

经过前期对火炮后坐过程中炮身与摇架的耦合运动的简化处理以及相关的理论分析，根据实验室现有的设备便可建立起符合后坐过程时变力学实验模型，即移动质量——悬臂梁时变力学模型。

2.1.1 实验机械系统

某实验室可提供小规模的模拟射击实验台，实验系统由移动质量块、支撑梁、驱动器、安装固定座、制动器以及固定支承附件等组成。结构如4 所示。

质量块在试验台上可沿着悬臂梁的方向依次完成三个阶段的运动。（1）质量块的加速运动，这个阶段是由驱动器提供能量，内部压缩气体的压力达到设定值前，卡锁装置将活塞杆固定锁紧。在驱动器内部压缩气体的压力达到设定值后，处于支撑梁端部的质量块在驱动器内部活塞杆的作用下加速运动；（2）质量块平稳运动。这一阶段，质量块脱离了活塞杆，在悬臂梁上做近似的匀速运动，本实验测量时变力学的过程就在这一阶段进行；（3）质量块减速运动。

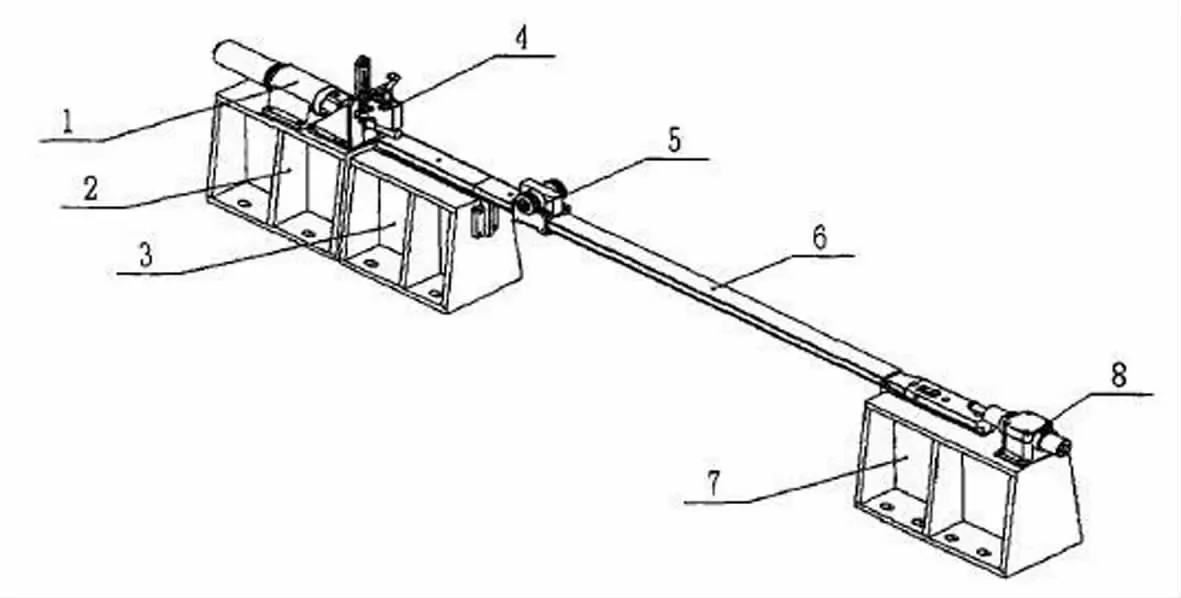
图4 试验机械系统结构简图

当质量块完成实验相关的运动以后，与试验台末端的制动器相撞击而逐渐停止运动。实验系统的机械部分如图5 所示。

图5 实验机械系统结构简图

2.1.2 实验测试系统

实验过程需要测量移动载荷在悬臂梁上运动时变力学的动态响应，因此除了实验机械系统以外，还需要相关的测量系统测量支撑梁的位置挠度以及应变随着时间的变化规律。

实验过程中使用数据采集器，将移动质量块沿着支撑梁运动的加速度信号作为触发源，根据后坐时间取采样频率f=10KHz，采样总点数m=10000 点。

在实验过程中移动质量块沿着悬臂梁做加速-近似匀速-减速直至停止的运动规律，当质量块移动到最大位移处，梁的自由端将产生竖直向上的最大挠度。本实验采用型号为LK-G400 的激光位移传感器来采集这个位置的最大挠度，测量范围大，分辨精度高，能够满足实验要求。

随着质量块在支撑梁上位移的变化，悬臂梁产生不同的应变规律。在实验台架距离悬臂梁左侧150mm和300mm位置上粘贴两处应变片，用以测量悬臂梁的应变规律，如图6 所示。

图6 悬臂梁上的应变片

同时为了测量质量块在悬臂梁上的运动规律，实验中采用高速摄影的方法在质量块上标记相关运动点，如图7 所示。

图7 质量块高速标记点

2.2 实验结果

将移动质量在悬臂梁上的运动规律在1 秒内采集到的数据进行拟合，得到如图8 所示的质量块的运动规律图。曲线在0.1 秒以后位移随着时间趋于正比增长，质量块近似匀速运动，与理论结果一致。

图8 自由端挠度实验和理论比较

将移动质量块在悬臂梁自由端的挠度实验采集到的数据和理论数值进行比较，得到如图9 所示的曲线图。

图9 质量块运动规律

将在实验台架150mm 和300mm 处应变动态响应的理论值和实验采集数值进行比较，曲线拟合如图10 和图11 所示。

图10 150mm 处应变对比曲线

图11 300mm 处应变对比曲线

从以上数据分析的图中可以看出，建立的时变力学实验模型采集的数据与火炮后坐过程理论计算结果基本一致，实验数据出现的偏差主要是实验系统中机械部分存在一定的间隙造成质量块在运动的过程中产生一定的振动，从而造成移动质量-悬臂梁模型的动态响应存在一定的误差。

3 结语

通过移动载荷建模理论[4]建立了火炮后坐时变力学系统，并利用现有实验条件搭建相应的移动质量-悬臂梁实验系统。通过实验测量悬臂梁的应变和自由端挠度随时间的变化规律，与理论结果拟合曲线相对比，验证了时变力学模型的正确性。