基于球壳模型的地壳应力与深度关系研究

刘兵权黎立云卫梦希王博楠王之东

1.中国矿业大学(北京)力学与建筑工程学院,北京 100083;2.煤炭资源与安全开采国家重点实验室,北京 100083;3.北京科技大学土木与资源工程学院,北京 100083;4.北京矿冶研究总院,北京 100160;5.国电联合动力技术有限公司,北京 100039

随着人类生产活动的发展,地壳中各种矿产资源的开发不断深入,煤矿开采深度已超过1 000 m,金属矿开采深度甚至超过2 000 m,由深部高地应力引起的岩爆、冲击地压等灾害表现得越来越剧烈[1],因而有必要对深部地应力变化趋势进行理论探讨,为深部工程地应力预测提供参考。

为了获得地应力场的分布数据,现有研究已提出很多高水平的测试方法[2],得到了许多宝贵的地应力实测数据,特别是深部地应力数据。 近些年,地应力数据大量更新,有必要建立更完善的理论模型。

关于地应力分布的理论分析,很多学者进行过研究[3-6]。 金尼克假说认为,垂直地应力为γH,水平地应力可通过假定水平应变为0,由胡克定理求得[7]。 Brown 等[8]基于多个国家和地区的地应力数据(深度多在1.5 km 以内,最深约为2.9 km),给出了垂直地应力与深度的线性回归关系(由此得出平均重度为27 kN/m3)和侧应力系数的包络线。 McCutchen[9]考虑了岩石自重,利用球壳模型求得了水平地应力和径向地应力与深度的关系,给出了侧应力系数,但没有结合实测数据进行拟合。也有研究利用岩石断裂强度来预测水平地应力的范围[10]。 这些研究在工程中广泛应用[11-13],但大部分研究未考虑自重体积力随深度变化的情况[14],也没有考虑内压的影响。

影响地应力分布的因素有很多,如地心引力、地壳内部高压力、构造运动、地形地貌、岩浆侵入、地温梯度、孔隙水压力、地球自转等[7]。 地壳深部完整性好于表面,浅层中由于板块运动、地形地貌的不均匀性对深部地应力的影响将逐渐减弱,应力分布主要由地壳整体的宏观力学条件决定。 因此,地应力与深度的函数关系需对起主要作用的岩体自重和地壳内部高压力综合分析得出,并通过大量实测数据拟合得到。 地温梯度和孔隙水压力引起的地应力变化是一种规律性的静水应力变化,地球自转引起的应力变化也在全球呈现规律性分布[15],因此均可叠加到拟合公式中;岩浆侵入等局部非均匀因素的影响则需根据实地情况考虑。

本文基于前人的研究工作做出以下补充和拓展:对地壳使用球壳模型,同时考虑了随深度变化的万有引力体积力和地球内部高压力对地壳应力变化趋势的综合影响,利用大量地应力实测数据对理论公式进行拟合,使之更好地应用于深部工程。

1 地壳宏观应力场理论推导

地球可近似视为球体,其半径为6 371 km。 地球的圈层结构由外至内可分为地壳、地幔、地核,其中地壳平均厚度约为17 km,主要由岩石构成;上地幔主要成分为岩浆,具有一定的流动性[16]。 在地壳尺度上,可以认为它满足弹性力学基本假设,因此参照弹性力学中球壳应力的解法来求得地壳应力分布。 地壳所受荷载为其中各质点所受的万有引力fr以及内部的高压力p[17],如图1 所示。 以地心为原点建立球坐标系,地壳区域总应力场为两部分荷载引起的应力场的叠加。

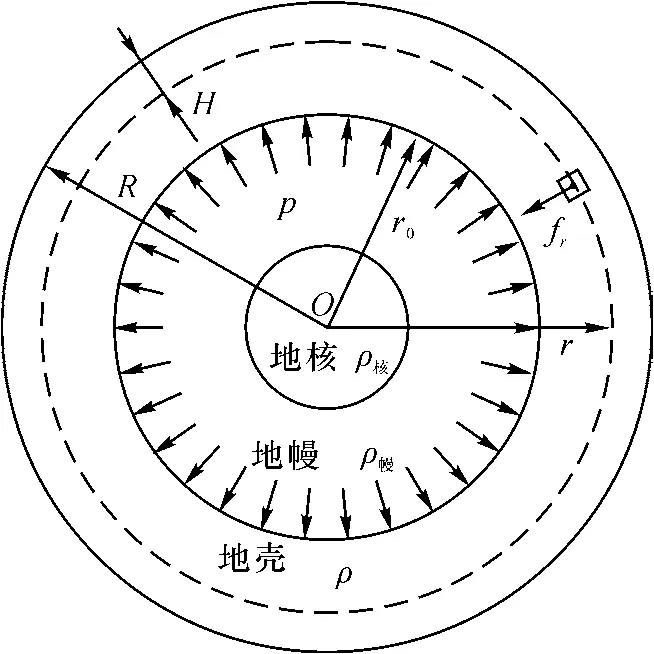
图1 地壳受载模型示意图Fig.1 Diagram of crustal loading model

由弹性力学可知,线弹性条件下受内压的无体力球壳的应力分布为[18]

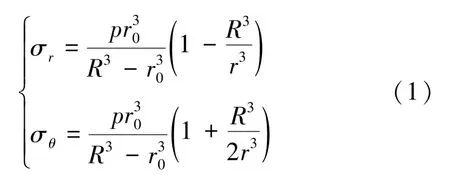
式中,σr为径向应力;σθ为环向应力;R为地球平均半径;r0为地壳与地幔交界处到地心的距离;r为该地壳单元体到地心的距离。

地壳内部具有极高的内压力p[17]。 由式(1)可知,若仅考虑p的作用,在整个地壳厚度上,环向地应力都为拉应力。 这显然与众多地应力实测数据不相符合。

在弹性力学理论中,对含有体力,尤其是考虑万有引力这种与距离有关的变体力情形鲜有讨论,弹性力学书籍中没有现成公式可用,因而需要重新推导。 对于球壳,引入自重体积力的作用,可能会使壳体中的各项应力分量都成为压应力。

根据弹性力学,球对称问题的平衡方程[18]为

如图1 所示,根据引力的高斯定理,与地心O相距为r处的地壳单元体,其所受的万有引力等于半径为r的球体对它的万有引力[14]。 鉴于地球的圈层结构,密度在同一圈层内比较接近,在不同圈层之间相差很大,因此将地壳部分的密度视为常数ρ。半径为r的球体的质量M可以用地球总质量M0与该球体以外的地壳质量的差来表示。 因此体力可以取为

式中,G为万有引力常数。

从式(3)可看出,体积力fr与r是非线性关系。

由球对称问题的几何方程和物理方程可以得到弹性方程为[18]

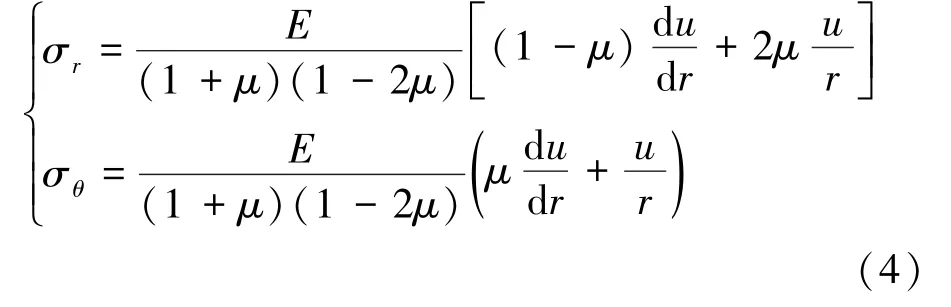
再将弹性方程式(4)和体力表达式(3)代入平衡方程式(2),可得

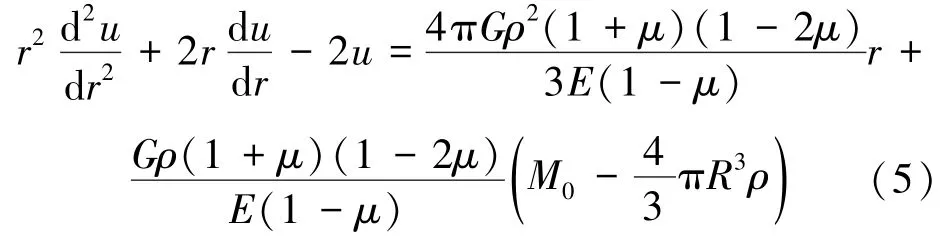
式(5)为常微分方程中典型的欧拉方程,其通解为

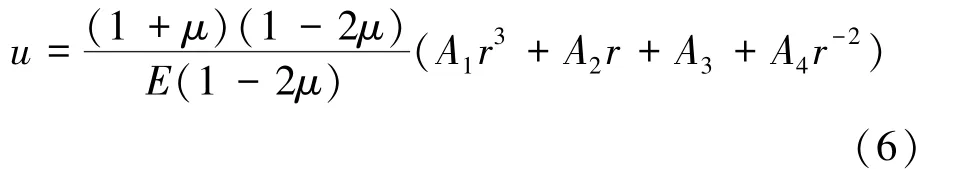
式中,A1、A2、A3、A4为待定系数。

其中,A1、A3可由式(6)代入式(5),r各幂次的系数对应相等得出

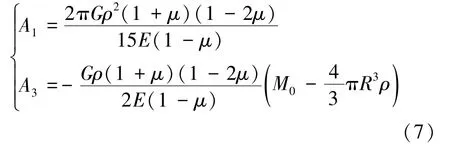
A2、A4需通过地壳的边界条件求解。

将式(6)代入弹性方程式(4),可以得到仅由变体力自重引起的应力场:

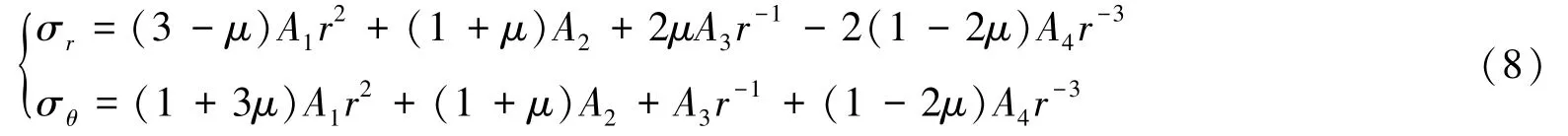
边界条件为

内压的作用已包含在式(1)中,这里地壳内表面的径向应力应为0。

由式(8)、(9)可得

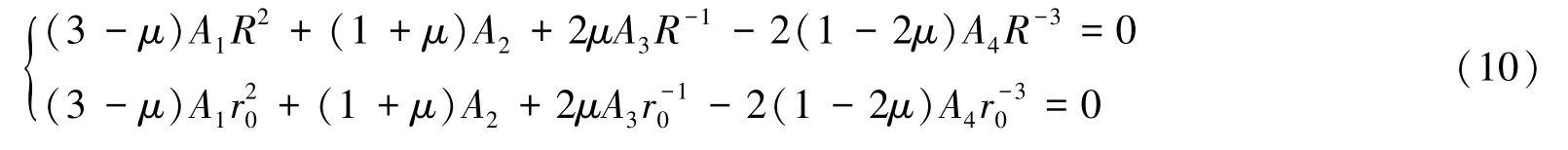
由此,可解出A2、A4:

将仅由变体力自重引起的应力场式(8)与由内压引起的应力场式(1)叠加,即可得到地壳内部总的应力场表达式:

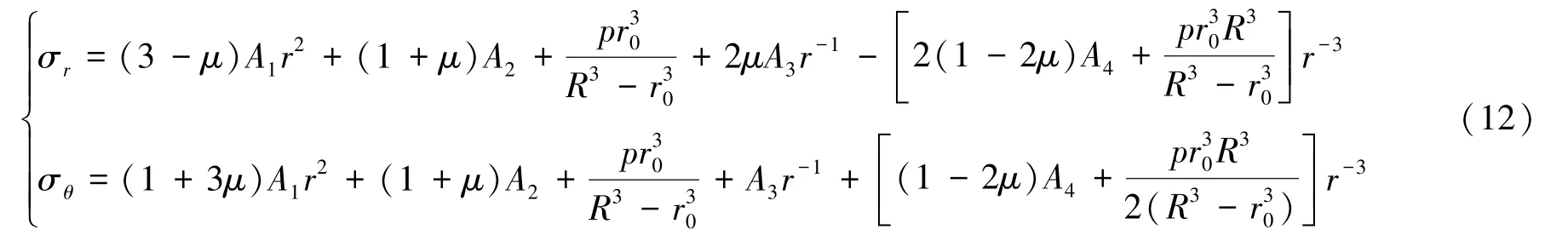
式(12)中各系数Ai为与地壳有关的宏观等效物理参数。 这些参数很难通过测量得到,但可以通过对现有的地应力实测数据拟合而求得。

可以看出,在地球尺度上,地壳应力分布与深度或半径并不是严格的线性关系;水平地应力与垂直地应力的表达式共用参数Ai,因此二者相互关联。

2 地壳应力场与深度的关系拟合

上一节基于弹性力学的推导,按弹性力学约定,应力σ以受拉为正。 为方便与地应力实测数据进行分析与比较,本文此后将地应力用s表示。按岩土力学约定,地应力s以受压为正。

在地应力的工程测量中,通常用sv表示垂直主应力,sH表示水平方向较大的主应力,sh表示水平方向较小的主应力,三者在多数情况下为正值,表现为压应力(在弹性理论中应为负值)。 由于构造等非均匀性因素的作用,这3 个主应力的方向并不严格与铅垂方向和水平方向相同,通常会有一个较小的倾角。 本文引用世界地应力图(WSM2016)[19]共404 条数据的3 向主应力都有说明倾角,其中2 个水平主应力倾角都不超过10°的数据共288 条,占71.3% 。 本文主要研究均匀性因素的作用,且多数倾角的数值较小、影响不大,在此忽略这个倾角的影响,将sH和sh取算术平均值sa,作为水平方向地应力值,即

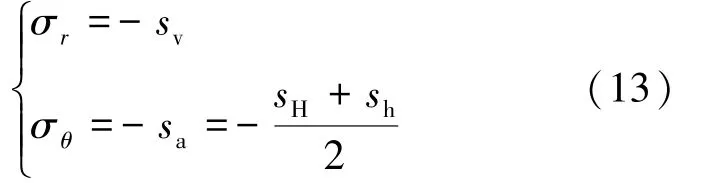
将式(12)中的多个常数合并,并结合式(13),得

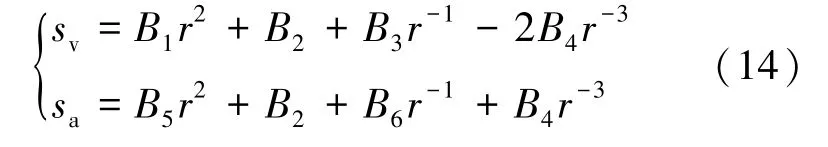
Bi和Ai的关系可以通过对比式(12) ～式(14)得到。

不同地区、不同深度下的地应力测量结果[19-31]见图2、图3 及附表1(篇幅所限,附表1 见于本刊网站)。 由于陆地地壳与海洋地壳的天然差异,并且现阶段能搜集到的海洋地应力数据较少,本文只引用陆地地应力数据并对其拟合。 由图1 可知

式中,H为深度,m。

通过式(15),可将测点到地心的距离r与深度H相互转化。

以式(14)作为拟合公式,利用附表1 中大量的地应力实测数据,应用最小二乘原理,通过MATLAB 计算得到参数Bi的值为

B1=-0.031 226,B2=1.083 0×107,B3=-8.372 5×1010,

B4=-4.628 0×1017,B5=0.119 45,B6=-2.670 4×1010。

最终得到垂直地应力sv和水平向地应力sa的数学表达式为

若将式(16)中r代换为H,会增加公式的复杂程度,为工程应用方便,只需得到地应力随测点半径r变化的表达式即可。

拟合结果表明,垂直地应力sv和水平地应力sa都随r的变小而增大,即两者都随深度H的增大而增大。 垂直地应力sv拟合曲线的标准偏差为6.44 MPa,拟合相关系数为0.898 4;水平地应力sa的拟合曲线标准偏差为8.19 MPa,拟合相关系数为0.867 3。

3 拟合结果对比分析

地应力的拟合结果对比如图2 和图3 所示。由水平地应力与垂直地应力的比值可以得出侧应力系数(图4)。

图3 水平地应力对比Fig.3 Comparison of horizontal in-situ stress

3.1 地应力拟合结果分析

图2 展示了各文献中垂直地应力实测值svm、本文拟合的sv曲线和依据金尼克假说得到的svγ曲线(重度取γ=22 kN/m3)的对比。 可以发现,在5 km 的深度之内(r>6 366 km),垂直地应力基本呈线性变化,与金尼克假说非常吻合;而Brown 和Hoek 使用线性拟合得到的平均重度为γ=27 kN/m3[8],这可能是拟合时引用的数据差异引起的结果。

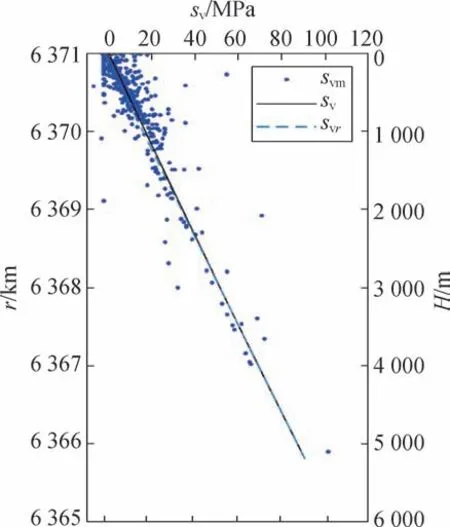
图2 垂直地应力对比Fig.2 Comparison of vertical in-situ stress

图3 为各文献中水平地应力实测平均值sam、本文拟合的sa曲线和依据金尼克假说得到的saγ曲线(重度取γ=22 kN/m3,侧应力系数取λ=0.9)的对比。 可以发现,水平地应力也大致呈线性变化。 本文所得平均水平地应力与金尼克假说比较接近,浅部相对差异较大,深部相对差异较小。

3.2 侧应力系数对比分析

图4 为各文献中侧应力系数实测值λm、本文得出的平均侧应力系数λ与Brown 和Hoek 给出的侧应力系数的包络线λmax、λmin的对比。 其中,侧应力系数是根据公式λ=sv/sa计算得出的。

图4 侧应力系数对比Fig.4 Comparison of lateral pressure coefficient

由图4 可以看出,深度超过约3 km(r＜6 368 km)时,本文得到的平均侧应力系数已高于Brown和Hoek 给出的侧应力系数上限,更接近于1;实测数据也大多超出此上限,分布在本文得出的λ曲线两侧。 这可能是Brown 和Hoek 原文缺乏超过3 km 深度的实测数据而导致的。

深度小于70 m(r>6 370.3 km)时,本文得到的平均侧应力系数会低于Brown 和Hoek 给出的侧应力系数下限,此时自重因素减弱而构造等非均匀性因素显著,水平应力分布离散,平均侧应力系数不具有代表性。 深度处于70 m ～3 km(6 368 km＜r＜6 370.3 km)时,平均侧应力系数落在上下限之间,和实际结果比较吻合。

图2 ～图4 中仍有一些较为离散的地应力实测值和侧应力系数值,说明在实际工程中该数据来源区域的构造、温度、孔隙水压力或其他因素比较显著,需要叠加这些因素的影响。

由式(16)可以得到地壳应力分布变化趋势图(图5)。 可以看出,在地壳更深处,地应力具有一定的非线性趋势,还需要基于大量深部地应力数据进一步研究。 内压会使得球壳内部产生环向拉应力,但通过拟合结果来看,自重等因素的作用使得平均地应力始终为压应力。

图5 地壳应力变化趋势示意图Fig.5 Diagram of crustal stress trends

4 结 论

(1) 在地球尺度上,地壳应力随深度的分布不再是线性关系,其理论关系符合式(12),水平地应力与垂直地应力相互关联。

(2) 垂直地应力sv和水平地应力sa都随深度H的增加而增大,随测点位置变化的拟合关系见式(16)。

(3) 在5 km 的深度之内,地应力基本随深度线性变化,地应力的大小与金尼克假说在γ=22 kN/m3、λ=0.9 时的结果最为接近,仅浅部的平均水平地应力差异较为明显。

(4) 当深度超过70 m 时,侧应力系数逐渐趋近于1,比较符合实际数据;当深度超过3 km 时,平均侧应力系数比Brown 和Hoek 给出包络线更接近实测数据;在近地表区域,侧应力系数分布离散,难以预估。

(5) 地壳内部的高压会引起水平方向产生拉应力,而自重引起的压应力更高,使得整个地壳厚度内的垂直地应力和水平地应力都为压应力。