长悬臂混凝土箱梁板单元模型计算分析

刘璐，韩扬，王建波，史文浩

长悬臂混凝土箱梁板单元模型计算分析

刘璐1，韩扬2，王建波1，史文浩3

（1.青岛理工大学 管理工程学院，山东 青岛 266520；2.中铁工程设计咨询集团有限公司 郑州设计院，郑州 450001；3.北京工业大学 城市建设学部，北京 100124）

为保证长悬臂混凝土箱梁的结构安全性，工程设计当中应建立简便有效的有限元模型予以验算。以某新建人行景观桥为工程背景，采用MIDAS/Civil、ANSYS等有限元模拟软件建立了多种模型，以期选取更加合理、准确的适合实际工程设计的长悬臂箱梁计算模型。通过提取各模型中的支反力及典型横截面应力进行对比分析可知，与单梁、梁格模型和实体单元模型相比，板单元支反力大小最接近实体模型的支反力，横向应力变化趋势与实体模型基本保持一致，更能直观反映长悬臂混凝土箱梁的空间效应。此外，为了保证长悬臂混凝土箱梁的结构安全性，研究了板单元模型在不同部位、不同状态下的应力分布差异，以及施加不同程度的横向预应力对长悬臂截面的受力影响。研究表明，箱梁长悬臂处的剪力滞效应十分明显。合理施加横向预应力束可以有效改善顶板应力状况，降低箱梁的剪力滞效应，保证梁体的受力安全。

长悬臂；箱梁；板单元模型；受力分析

随着城市现代化建设的飞速推进，各类高架、立交桥不断涌现，这些桥梁在设计时不仅要满足市内日益增长的人车通行需求，还要兼顾结构外形的美观大方以及同周边环境的协调性[1]。在这之中，长悬臂混凝土箱梁桥是被广泛应用的结构形式之一，该类型箱梁桥具备常规混凝土箱梁的稳定性和可靠的抗弯扭力学性能，但为了减轻结构自重、调节内力分布，其内部通常采用大箱室加长悬臂的构造截面，主梁宽度较大[2]。

由于宽跨比偏大、横向悬挑臂较长，空间效应显著，长悬臂箱梁在横桥向上的应力分布相当复杂，现行公路桥梁设计规范中惯常采用的初等梁理论计算并不能有效分析出梁体局部的翘曲、畸变及剪力滞效应，因此在开展相关设计工作时往往需要借助有限元软件对结构受力进行数值模拟分析[3]。

目前，长悬臂箱梁桥的模拟计算方法主要包括以下几种：①空间梁单元模型法（即单梁模型法）；②空间梁格模型法[4]；③板单元模型法；④实体单元模型法。方法①是基于平面杆系单元的结构离散性分析，主要通过荷载横向分布对梁体进行内力验算，没有考虑空间效应，使用时存在局限性。方法②则通过划分等效的梁格单元模拟桥梁上部，使箱梁各区域内的抗弯扭刚度集中至临近梁格中，从而计算得到结构局部的内力与位移。方法③的建模要素以板单元为主，为了解决宽箱梁的空间效应问题，可通过共用节点的方式在板单元之间添加虚拟梁单元（即杆系单元），以便于模型内部施加多向预应力。方法④是上述模型中最有效的结构受力分析方法，实体模型可以更加精准、细致地反映结构内力状态，但该方法的模型分析复杂、理论水平要求较高，且建模运算费时费力，在实际工程设计中不易推广。

本文以工程实例为背景，利用MIDAS/Civil、ANSYS等软件对长悬臂混凝土箱梁桥的不同模型进行比对，分析板单元计算模型的合理性、精确性；同时，通过在模型当中施加横向预应力，模拟箱梁截面长悬臂的应力分布状况。此研究可为同类型桥梁的设计验算提供参考依据，兼具良好的理论研究意义和实际应用价值[5]。

1 建立模型

1.1 工程概况

某市一跨江人行景观桥为4孔预应力连续刚构桥，桥梁全长133.5m，跨径布置为（27.6+36.6+36.6+27.6）m，平立面布置如图1所示。其中，边墩盖梁处采用盆式橡胶支座进行支撑，中墩与梁体固结。

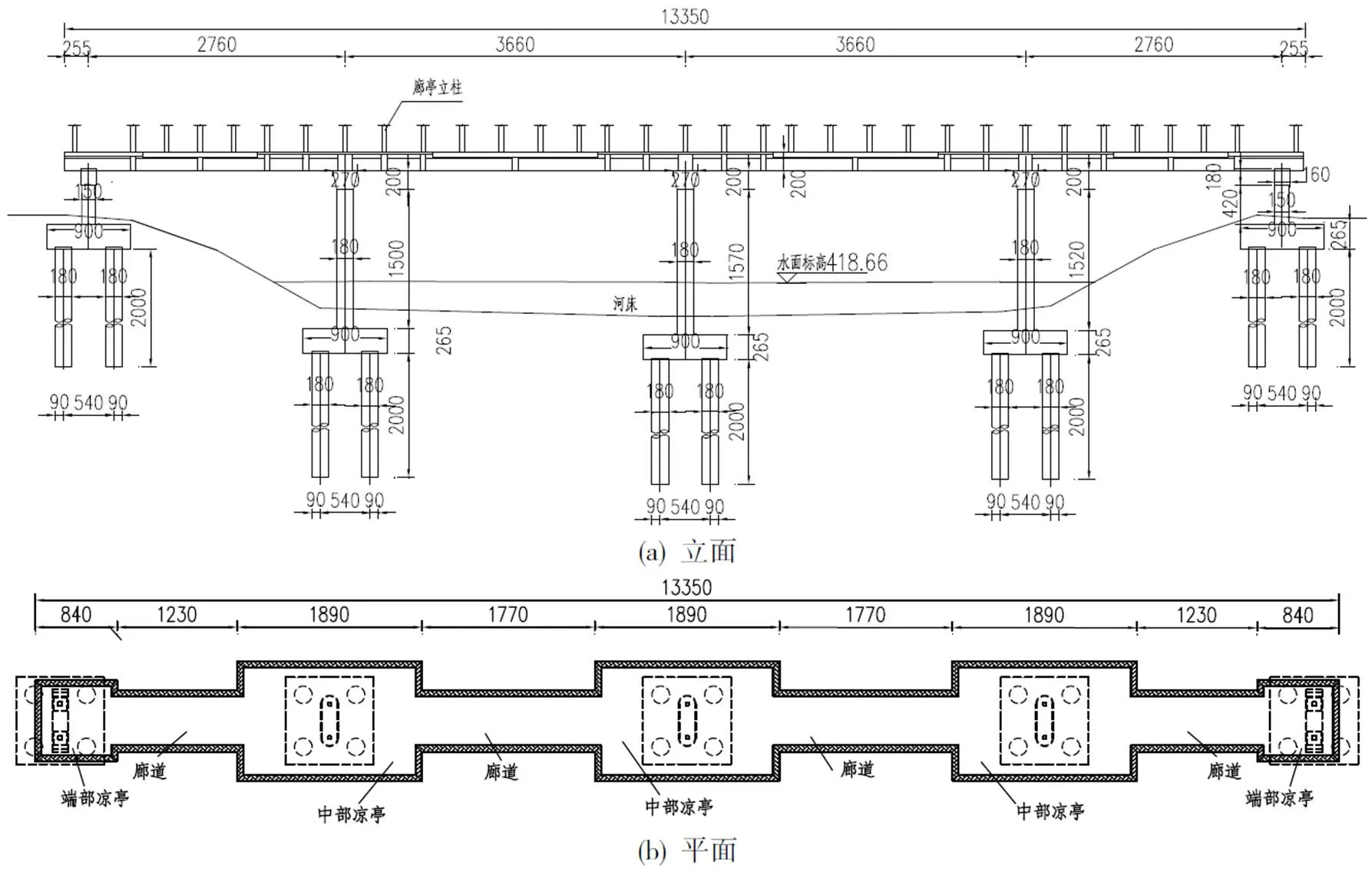
图1 桥型布置图（单位：cm）

桥梁上部结构采用等高的单箱单室混凝土箱梁，混凝土强度等级C55，设计标准为A类预应力构件。为满足桥面廊道、凉亭等步行景观的设计需求，全桥共采用了3种不同宽度的箱型截面，如图2所示。其中，廊道处顶板宽6.4m，悬臂长0.75m；边墩凉亭处顶板宽8.4m，悬臂长1.75m；中墩凉亭处顶板宽12.4m，悬臂长3.75m。由于中墩处箱梁翼缘过长且部分凉亭立柱坐落在悬臂端，故于顶板内设置了横向预应力钢束，以此来加强桥面横向刚度、消除空间效应。

本文将该桥作为数值模拟算例，按照设计图纸与规范要求利用MIDAS/Civil建立单梁模型、梁格模型和板单元模型，并通过ANSYS软件建立实体模型进行对比分析。

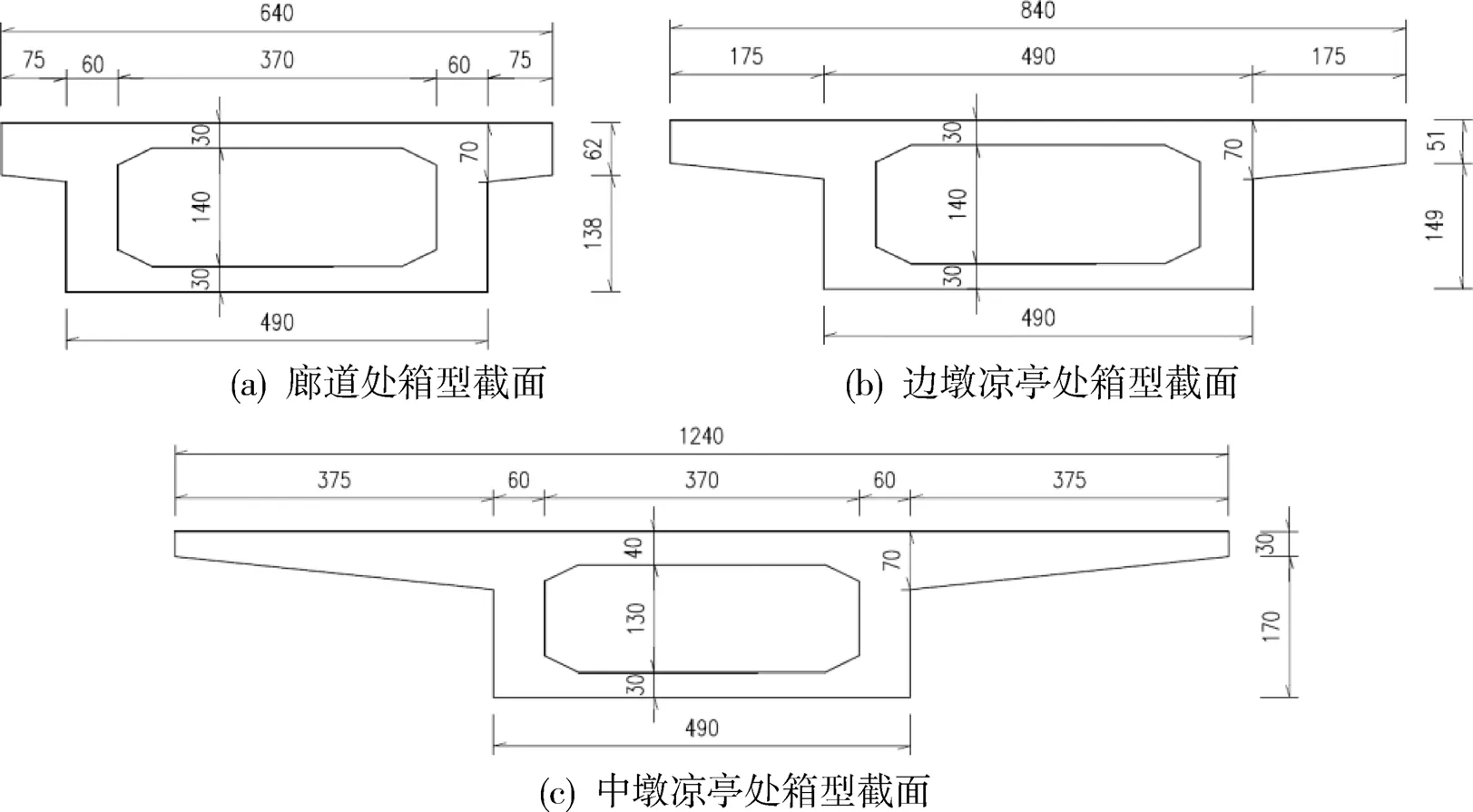
图2 主梁横截面图（单位：cm）

1.2 单梁模型

通常情况下，当桥梁的宽跨比较小、空间效应偏弱时，结构在荷载作用下所产生的横向弯曲扭转可忽略不计，梁体常被视为一维杆系进行纵向受力计算。该桥便以此为理论基础建立了单梁模型，共采用14个计算截面，包含215个节点和114个杆系单元，模型整体结构如图3所示。

图3 单梁模型

1.3 梁格模型

梁格法是一种空间模拟计算的近似方法，其建模核心是以等效的梁格代替一维杆系单元，将实际结构中的纵、横向刚度分别集中于临近梁格内。梁格体系最为理想的刚度等效结果是所有梁格的内力、位移等计算结果均与梁体对应部位的实际状况保持一致，但作为一种考虑横向受力的二维杆系模型，其本质上仍是对实体构造的简化模拟，只是此类模型的模拟偏差往往处于常规设计工作的允许范围内[6]。

根据剪力-柔性梁格法的基本原理，本桥梁格模型的计算细节如下：

（1）所有箱型截面沿顶底板居中切断，纵向梁格的中性轴与原箱型截面保持一致，其抗弯惯性矩仍根据原截面主轴进行计算。

（2）原箱型截面总扭矩由各纵向梁格的顶底板扭矩及腹板剪力流组合而成，故梁格截面的抗扭刚度仅代表顶底板抗扭刚度，其单宽抗扭惯性矩计算公式为

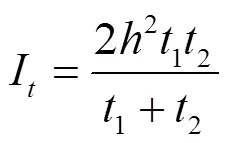
其中，1,2分别为顶底板厚度；为顶底板中线间距。

（3）纵、横向梁格的截面特性计算原则基本相同。横向梁格构件均为工字型截面，包括箱梁横隔板与虚拟横梁，其中虚拟横梁无自重且腹板厚度趋近于零。

（4）横向梁格间距不超过纵梁腹板间距。

依照上述假定建立了本算例的梁格模型，如图4所示。此模型共采用44个计算截面，包含509个节点和559个单元。根据桥面变宽及桥上凉亭立柱的布置形式，主梁沿顺桥向每间隔1.5m或2.1m划分单元并设置横梁，中墩凉亭处的虚拟横梁内添有横向预应力钢束。

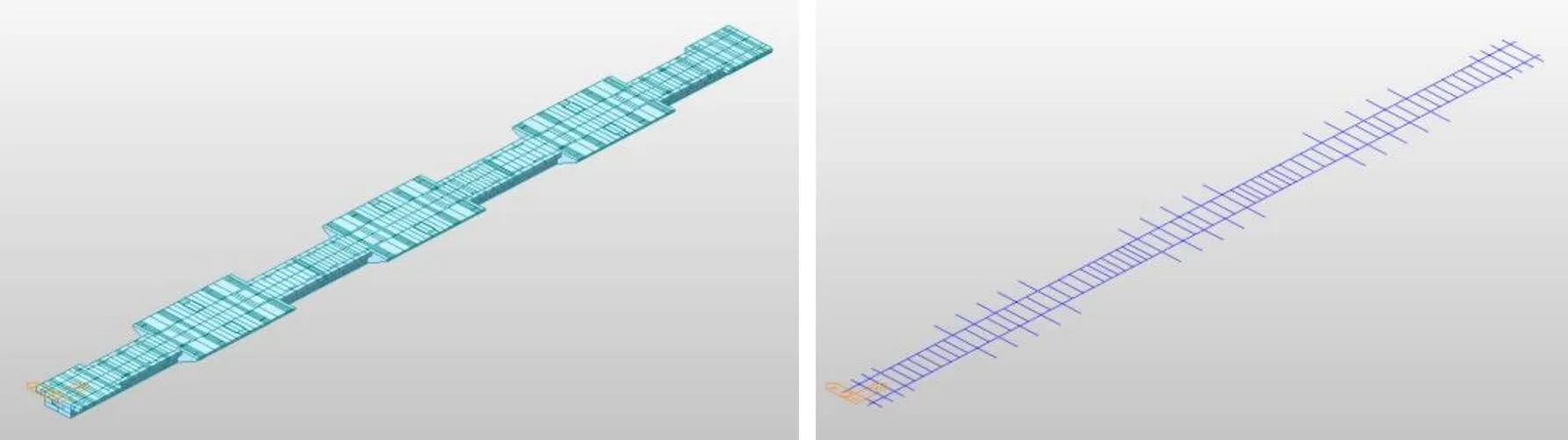
图4 梁格模型

1.4 实体模型

为验证上述模型在空间应力计算中的准确性，本文还对比了ANSYS软件计算的实体单元模型，如图6所示。实体模型中的梁体、墩柱等主要结构采用SOLID 95单元，体内预应力钢束采用LINK 8单元。该模型整体采用了“点—面—体”的建模思路，共包含1043342个节点和230156个单元。在模型当中，凉亭处的双向预应力短束通过体模型切割的方法进行定义，全桥通长的纵向预应力长束采用导入单元并耦合节点的方法进行定义，预应力钢束的荷载作用主要依靠调控单元温度对混凝土结构产生压力来进行等效模拟[7]。

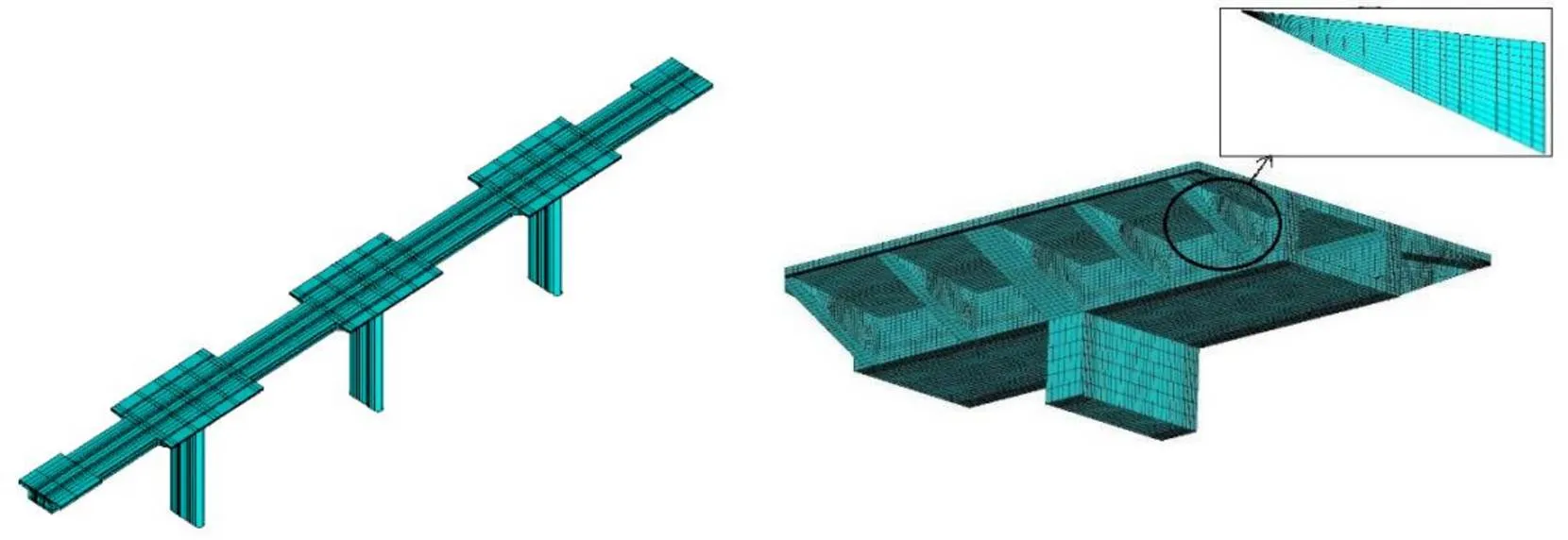
图5 实体模型

1.5 板单元模型

此模型中的实体结构全部由板单元（厚板）组成，梁体局部构造决定了各部位的板单元厚度。根据局部构造划分单元网格时，跨中网格密度基本为1m，靠近桥墩中线、凉亭立柱、预应力钢束等位置时网格则需进一步细分，以满足施加恒载、张拉预应力、墩梁固结等节点使用需求。在模型当中，梁体顶板、腹板均借助虚拟梁单元张拉双向预应力钢束，这些虚拟梁单元采用无自重且截面微小的杆系单元，通过与主梁的共用节点将所施加的预应力荷载传递给板单元模型。该模型共采用了17种板厚，其中包含8643个节点、8804个板单元以及2570个虚拟梁单元，如图5所示。

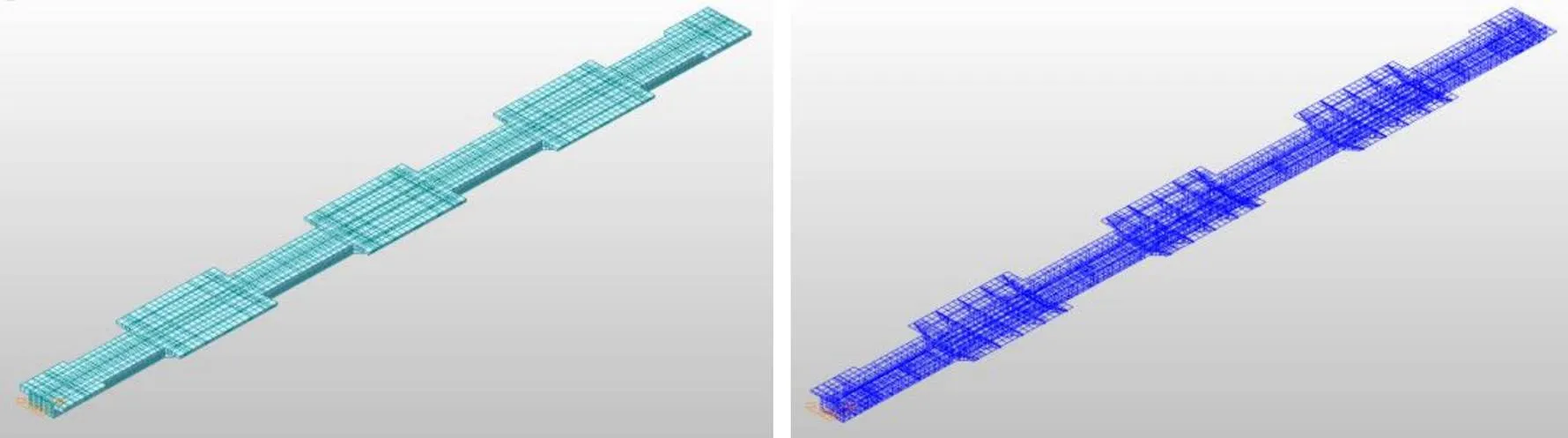
图6 板单元模型

2 模型对比分析

为了研究板单元模型的可行性及精确性，需将各有限元模型的计算结果进行对比分析。首先提取支反力[8]。将板单元模型的支反力同单梁模型、梁格模型、实体单元模型的支反力进行对比，判断模型准确性与变化规律；然后将各模型典型截面处的法向应力进行比对，通过分析模型在横桥向的应力分布差异，得出板单元模型的计算结果较为接近实体模型，可以直观反映长悬臂混凝土箱梁的空间效应。

2.1 支反力结果对比

为验证所建模型的可靠性，现将单梁、梁格、实体模型与板单元模型在成桥阶段的支反力大小进行对比（见表1）。

表1 各模型支反力结果对比

从表1支反力对比数据可知，板单元模型与其他模型差值在10%以为，满足工程精度要求。表明模型建立及相应参数设置准确，边界条件模拟无误。

为了更直观展示支反力区别，提取各模型的支反力绘制曲线，如图7所示。

从图7可知，跨中墩支反力要比1/4与3/4墩大，表明跨中墩是主要承重构件。在1/4墩、跨中墩及3/4墩各个模型的支反力变化情况相同，单梁与梁格支反力较板单元相比偏大，就数值上说，板单元支反力大小最接近实体模型的支反力。从图7可知板单元相较于单梁和梁格模型能更加精细的模拟结构受力。

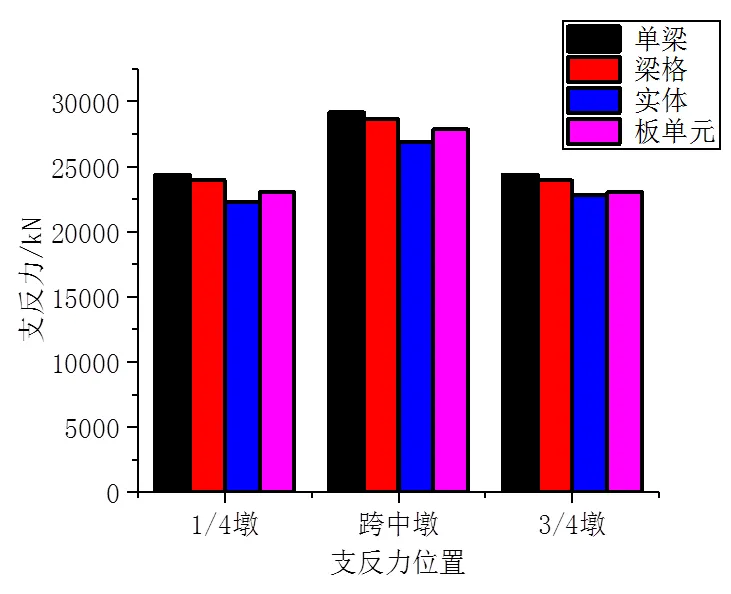
图7 支反力对比图

2.2 典型截面应力分析

为探明各个模型的细部受力情况，提取箱梁桥第2孔跨中及跨中墩墩顶梁体横向顶底板法向应力进行比较。截面示意图如图8, 9所示，应力分析结果如图10, 11所示。

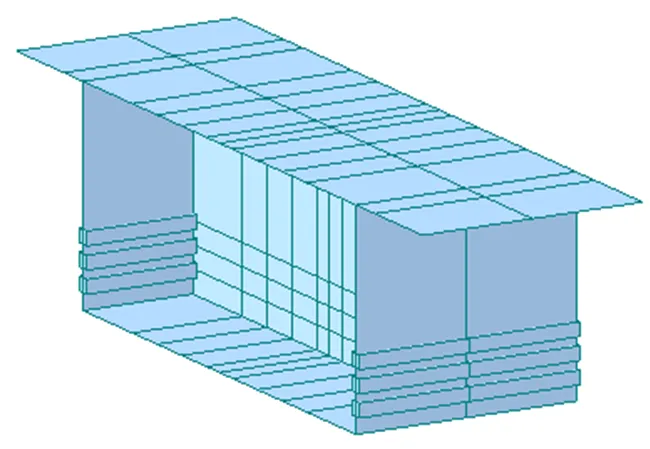
图8 第2孔跨中截面示意图

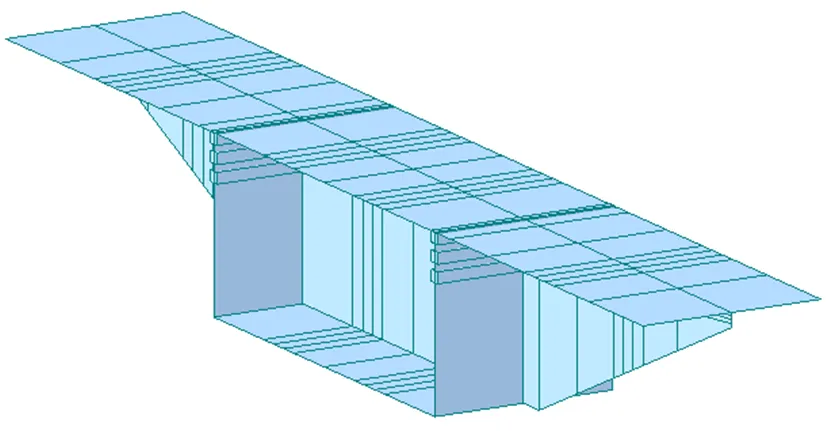
图9 跨中墩墩顶截面示意图

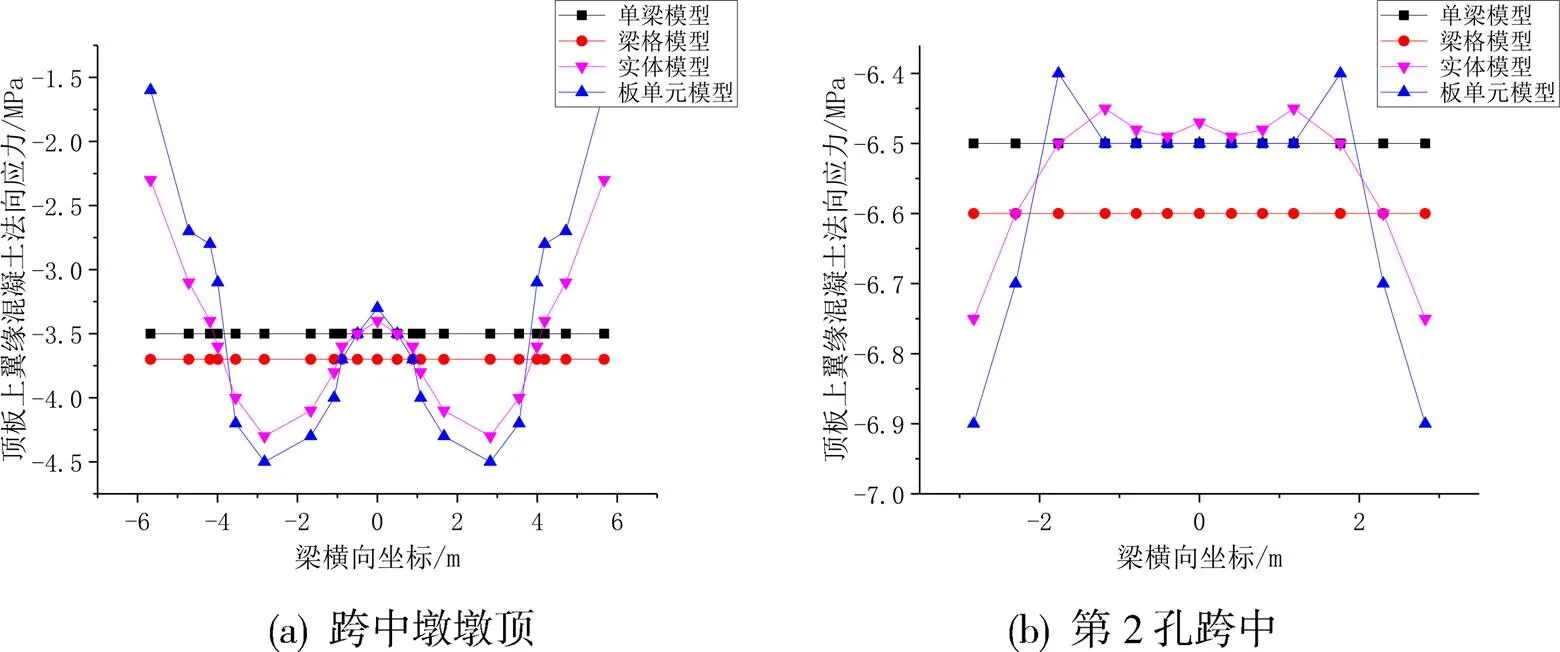
图10 各模型顶板法向应力对比图（图中正值为拉应力，负值为压应力，以下同上）

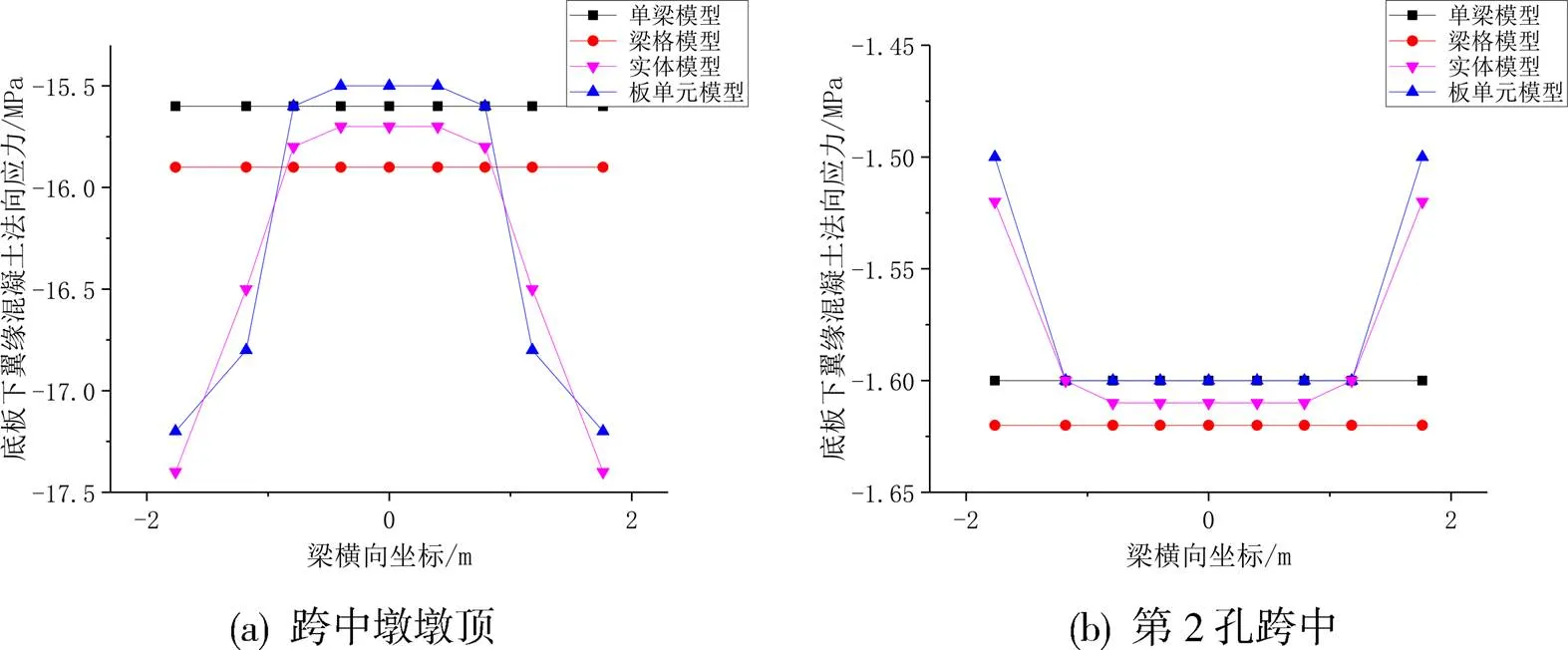
图11 各模型底板法向应力对比图

由图10, 11对比可知，箱梁墩顶截面在顶板处的应力变化幅度要大于底板，而箱梁顶底板在墩顶截面处的应力变化幅度要大于跨中截面。图10表明，板单元模型梁体顶板上翼缘应力变化幅度接近3.0MPa，跨中梁顶板上翼缘应力变化幅度仅为0.5MPa；图11表明，板单元模型梁体底板下翼缘应力变化幅度接近2.0MPa，跨中梁底板下翼缘应力变化幅度仅为0.1MPa。此外，板单元模型与实体模型在墩顶截面顶底板相同位置处的法向应力最大差值分别为0.6MPa、0.3MPa，在跨中截面顶底板相同位置处的法向应力最大差值分别为0.3MPa、0.1MPa，板单元模型计算结果相对趋于保守。

根据应力分布图及上述分析可知，杆系单元模型中的梁体截面仅由单节点或双节点表示，并不能确切反映横向梁体的应力变化情况；板单元模型的梁体截面则由杆系组成，可以有效反映梁体横向应力的分布情况，且其应力变化趋势与实体模型基本保持一致，能够满足工程设计使用需求。

3 长悬臂局部受力分析

3.1 剪力滞后效应

对于空腹式悬臂箱梁来讲，由于截面受力时是通过腹板来传递剪力，横向梁体变形存在滞后效应，腹板区域应力分布为抛物线形状，而非普通的线性分布情况（见图12）。因此在靠近腹板区域的应力较大即为正剪力滞，若工程中不考虑腹板处的应力增大，设计不合适容易导致翼缘板与腹板交接处开裂，影响结构安全[9]。

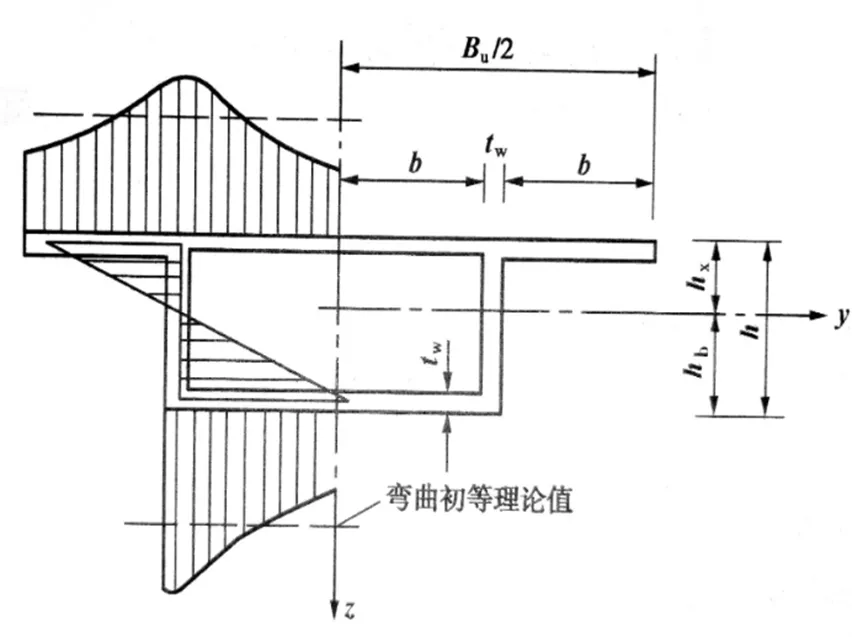
图12 箱梁剪力滞效应示意图

图12中，为翼缘板宽度；t为腹板厚度；B为顶板宽度；为截面高度；h以及h分别为中性轴以上和以下的截面高度。

3.2 长短悬臂截面应力比较

在成桥阶段，由于对于墩顶长悬臂截面施加了横向预应力，因此，为了降低变量，本次比较长悬臂截面和短悬臂截面应力变化，选取了无横向预应力的第2跨长悬臂截面与短悬臂截面进行应力对比。应力对比结果如图13所示。

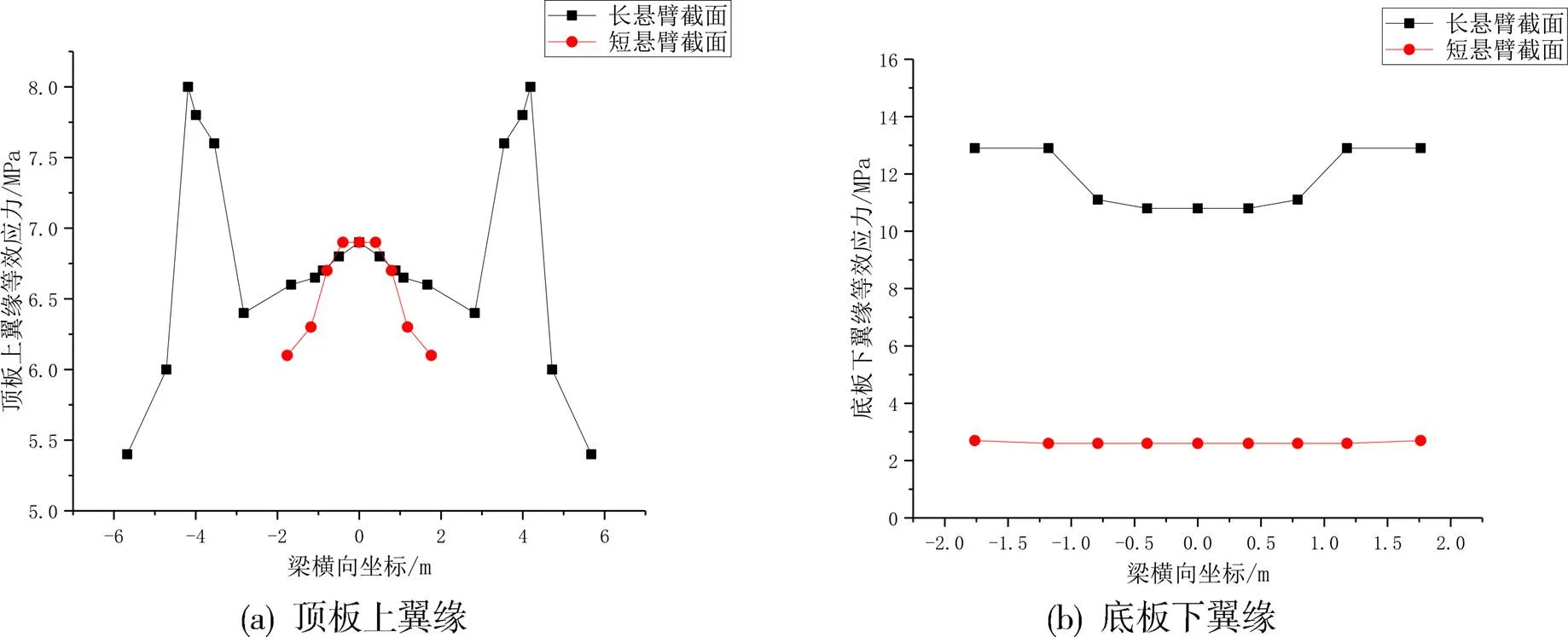
图13 长短悬臂截面应力对比图

从图13(a)可知，顶板上翼缘长悬臂截面等效应力在5.4～8.0MPa之间，短悬臂截面等效应力在在6.1～6.9MPa之间，长悬臂截面应力变化幅度较大，相较于短悬臂截面高出2.25倍，这说明长悬臂截面受力更大。长悬臂截面应力变化从悬臂端至腹板位置逐渐增大，从5.4MPa增大至8.0MPa，自腹板位置向居中位置先减小后增大，应力从8.0MPa降低至6.4MPa后又提高至6.9MPa，应力横向呈对称分布，长悬臂截面在腹板位置应力变化明显，表现出了明显的剪力滞效应。短悬臂截面在悬臂端位置等效应力为6.1MPa，在居中位置为6.9MPa，变化幅度相对较小，剪力滞效应相对不明显。

从图13(b)可知，底板下翼缘等效应力在10.8～12.9MPa之间，相对于顶板应力变化较缓；腹板位置应力为12.9MPa，居中位置等效应力为10.8MPa，同样表现出明显的剪力滞效应。短悬臂截面等效应力在2.6～2.7MPa之间，腹板位置应力为2.7MPa，居中位置等效应力为2.6MPa，等效应力较低，同时剪力滞效应不明显。

为了更直观地反映板单元模型在箱梁横向受力的特点，提取了第2跨跨中相邻长短悬臂截面的等效应力云图如图14所示。

从图14可知，长悬臂截面等效应力变化范围在2.1～8.3MPa之间，短悬臂截面等效应力变化范围在1.6～3.1MPa之间，长悬臂截面应力变化明显。同时，长短悬臂均表现出了一定程度的剪力滞效应，在腹板位置的顶底板应力大，其余位置相对较小。另外，长悬臂截面的剪力滞效应相较于短悬臂截面来说在顶板与底板均表现得更为明显。

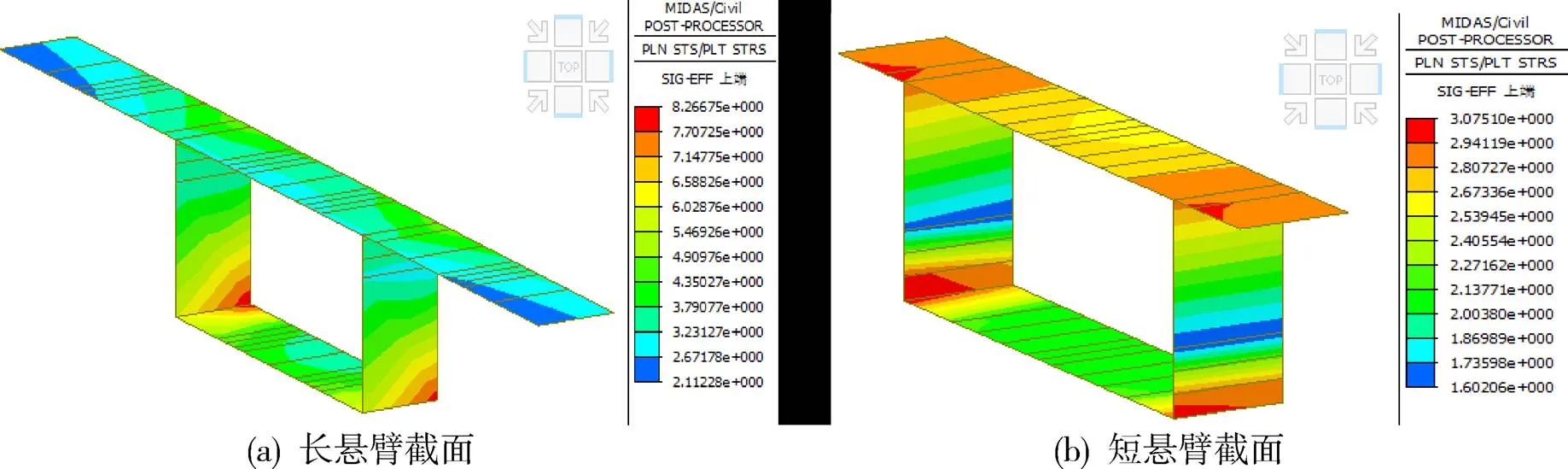
图14 长短悬臂截面等效应力对比云图

综上，针对于长短悬臂截面应力可得到如下结论，长短臂截面顶底板均表现出剪力滞效应，靠近腹板位置应力更大；长悬臂截面较短悬臂截面的剪力滞效应更明显；长悬臂截面与短悬臂截面顶板相较于底板来说应力变化更大；长悬臂截面受力更大，应力相对于短悬臂截面较大[10]。

3.3 施加横向预应力对于长悬臂截面的影响

对于长悬臂截面，上方景观亭的柱力较大，作用于长悬臂截面时在长悬臂截面悬臂根部产生较大的弯矩，从而产生较大拉应力，根部容易开裂，因此，在长悬臂截面位置相应设置了横向预应力钢束，通过预应力张拉产生的正应力中和弯矩产生的正应力，从而保证截面安全。

为分析横向预应力施加对于长悬臂截面影响，提取了横向预应力钢束的施加位置的长悬臂截面，提取施加预应力荷载时顶板以及底板的法向应力进行比对，同时将不同程度的预应力荷载施加到梁体，用以比较不同程度的预应力对于梁体受力所产生的影响，具体结果如图15, 16所示。

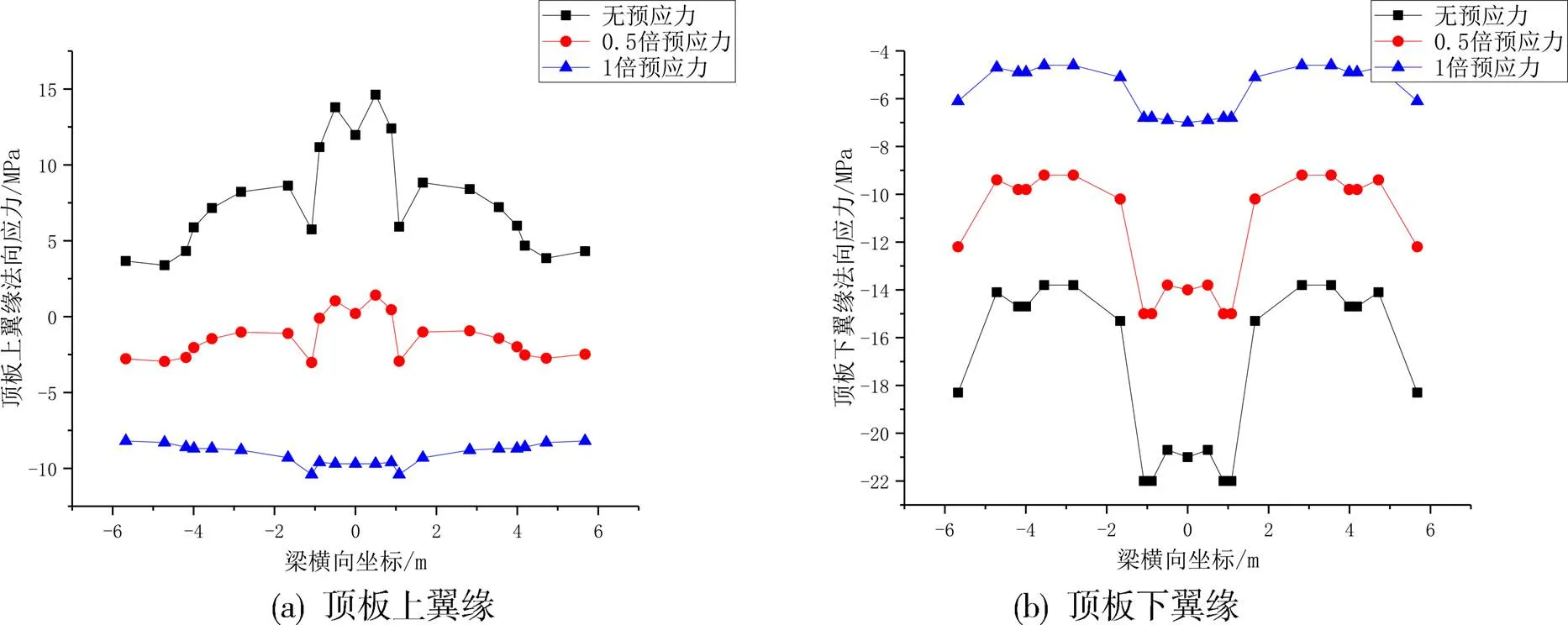
图15 长悬臂截面顶板法向应力

从图15(a)可知，对于上翼缘，在未施加预应力时，顶板法向应力为正值，范围为3.7～14.6MPa，靠近腹板位置具有明显剪力滞效应，应力较悬臂端增大了接近5.0MPa，居中位置应力最大，同时应力变化也最为剧烈，法向应力增大了接近10.0MPa，这样受力对于截面会产生不利影响。施加0.5倍预应力后，应力变化范围明显减弱，范围为0.0～5.0MPa，剪力滞效应降低，靠近腹板位置变化范围为2.0MPa，居中位置应力增大2.5MPa左右，较未施加预应力降低了3倍。在施加1倍预应力后，应力变化降低至2.5MPa，应力由正值变为负值，说明此时截面受压，法向应力范围自-10.0～-7.5MPa，腹板位置剪力滞效应基本消除，居中位置应力突变基本消除。

从图15(b)可知，对于下翼缘，在未施加预应力时，顶板法向应力为负值，范围为-22.5～-13.8MPa，靠近腹板位置具有明显剪力滞效应，应力较悬臂端增大了接近5.0MPa，居中位置应力最大，同时应力变化也最为剧烈，法向应力增大了接近10.0MPa，这样受力对于截面同样会产生不利影响。施加0.5倍预应力后，应力变化范围明显减弱，范围为-15.0～-8.0MPa，剪力滞效应降低，靠近腹板位置变化范围为4.0MPa，居中位置应力增大7.0MPa左右。在施加1倍预应力后，法向应力范围自-8.0～-4.0MPa，腹板位置剪力滞效应降低显著，应力较悬臂端增大了仅接近1.0MPa；居中位置应力突变同样大幅度降低，差值为2.0MPa。

从图16(a)可知，无预应力状态下，底板上翼缘法向应力变化范围在-2.5～-2.2MPa，剪力滞效应较低，幅度仅为0.3MPa；横向截面各个位置应力变化幅度较低，应力变化平缓。施加0.5倍预应力后，上翼缘法向应力变化范围在-2.2～-1.9MPa，压应力降低。施加1倍预应力后，法向应力变化范围在-1.7～-1.5MPa，压应力继续降低，应力变化幅度改变不大。

从图16(b)可知，在没有施加预应力状况下，底板下翼缘法向应力变化范围在1.7～2.5MPa，应力自腹板位置至居中位置逐渐减小，剪力滞效应带来的应力变化幅值为0.7MPa。在施加0.5倍预应力状况下，底板下翼缘法向应力变化范围在1.5～2.2MPa，应力自腹板位置至居中位置逐渐减小，剪力滞效应带来的应力变化幅值为0.6MPa，拉应力降低。在施加1倍预应力状况下，底板下翼缘法向应力变化范围在1.3～1.7MPa，应力自腹板位置至居中位置逐渐减小，剪力滞效应带来的应力变化幅值为0.4MPa，拉应力降低。

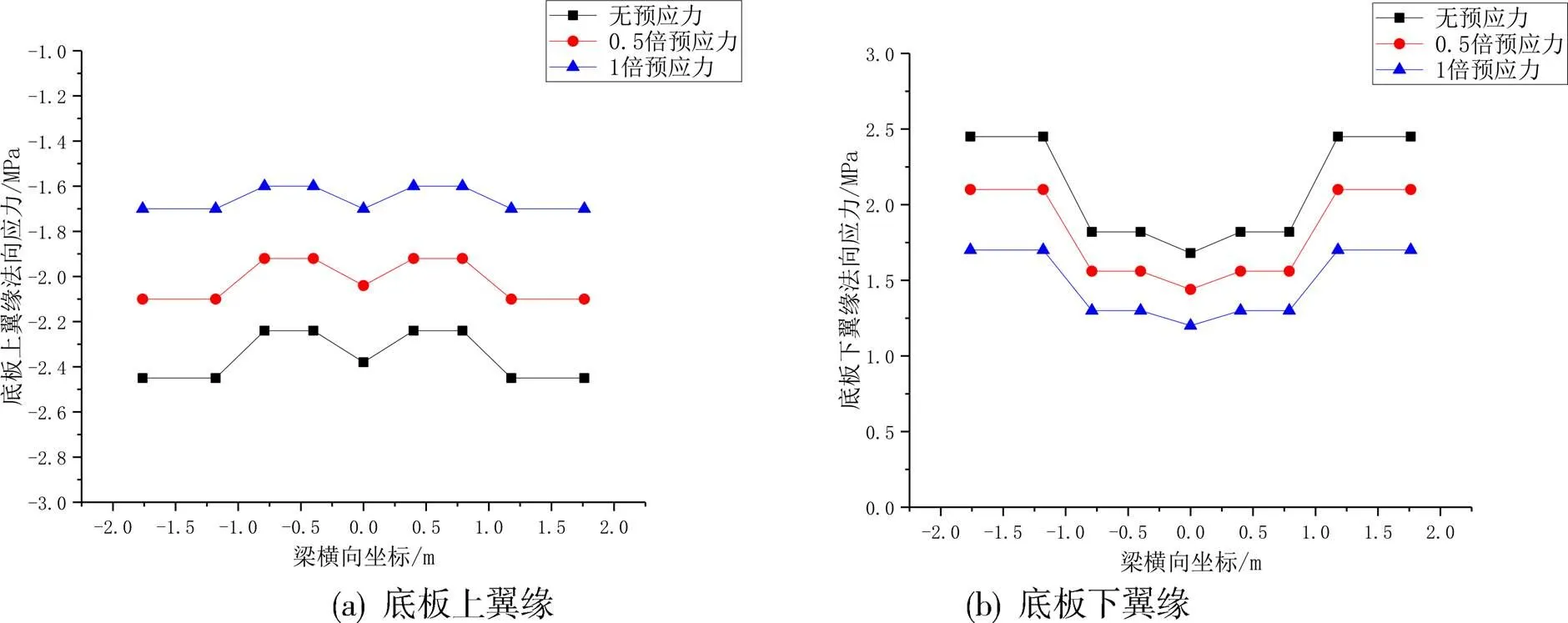
图16 长悬臂截面底板法向应力

从图15与图16对比可知，横向预应力的施加对于顶板作用大于底板，顶板与底板上翼缘和下翼缘的应力变化趋势相反，符合梁体横向、纵向受力的特点。

从以上分析结果可知，横向预应力束的施加可以有效改善顶板应力状况，施加1倍预应力可保证长悬臂截面顶板整体受压；降低箱梁的剪力滞效应；改变截面的应力突变情况，保证梁体的受力安全。

4 结论

（1）通过提取各模型中的支反力及典型横截面应力进行对比分析可知，与单梁、梁格模型和实体单元模型相比，板单元支反力大小最接近实体模型的支反力；横向应力变化趋势与实体模型基本保持一致，更能直观反映长悬臂混凝土箱梁的空间效应。同时，该模型相较于实体模型操作更加简便、易于推广，可以在满足设计精度需求的条件下指导工程实践。

（2）通过研究箱梁的空间横向应力分布可知，长短臂截面顶底板均会出现剪力滞效应，靠近腹板位置应力更大；长悬臂截面较短悬臂截面的剪力滞效应更明显；长悬臂截面与短悬臂截面顶板相较于底板来说应力变化更大；长悬臂截面受力较大，应力相对于短悬臂截面更大。

（3）对于长悬臂的细部构造来说，施加横向预应力束可以有效改善顶板应力状况，施加1倍预应力可保证长悬臂截面顶板整体受压，降低箱梁的剪力滞效应。因此，合理调整箱梁的横向预应力束布置，可以保证长悬臂截面顶板处于整体受压状态，有效改善长悬臂的应力分布，保证梁体的受力安全。

[1] 李春宝，程旭东，俞然刚，等. 桥梁结构模型试验教学平台设计与开发[J]. 实验技术与管理，2021, 38(04): 116-120, 127.

[2] 彭崇梅，李小年，赵勇. 在役大悬臂箱梁桥顶板加劲腋纵向开裂成因分析[J]. 公路，2017, 62(04): 75-78.

[3] 冀伟，孙斌，白倩，等. 长期荷载作用下钢-混凝土组合梁的挠度计算与分析[J]. 湖南大学学报（自然科学版），2021, 48(07): 51-60.

[4] 宋嘉宇，邬晓光. 基于梁格法对曲线箱梁桥的有限元分析[J]. 公路，2021, 66(07): 134-138.

[5] 苏红军. 混凝土箱梁桥剪应力偏载系数简化计算方法[J]. 中外公路，2020, 40(01): 155-159.

[6] 杨圣超，夏兴佳. 基于梁格法的预制箱梁横向刚度模拟研究[J]. 世界桥梁，2018, 44(02): 73-76.

[7] 伍彦斌，黄方林. 空间预应力钢束平滑建模及张拉过程模拟方法[J]. 应用力学学报，2017, 34(02): 291-296, 404.

[8] 宋旭明，李梦然，赖明苑，等. 加劲长悬臂板混凝土箱梁施工阶段受力状态优化[J]. 华南理工大学学报（自然科学版），2020, 48(10): 67-75.

[9] 张玉元，张元海，张慧，等. 考虑边界约束影响的薄壁箱梁剪力滞翘曲应力分析[J]. 应用基础与工程科学学报，2019, 27(05): 1042-1053.

[10] 周建民，何余良，吴旭东，等. 体外预应力索加固预应力混凝土连续箱梁桥方案比较[J]. 工业建筑，2017, 47(03): 182-187.

Calculation and analysis of plate element model of long cantilever concrete box girder

LIU Lu1，HAN Yang2，WANG Jian-bo1，SHI Wen-hao3

(1.School of Management Engineering, Qingdao University of Technology, Shandong Qingdao 266520, China;2.Zhengzhou Design Institute, China Railway Engineering Design and Consulting Group Co., Ltd., Zhengzhou 450001, China;3.Department of Urban Construction, Beijing University of Technology, Beijing 100124, China)

In order to ensure the structural safety of long cantilever concrete box girder, a simple and effective finite element model should be established in engineering design. In this paper, taking a newly built pedestrian landscape bridge as the engineering background, MIDAS/Civil ANSYS and other finite element simulation software was used to establish single beam, grillage, solid and plate element of the long cantilever box girder, in order to select a more reasonable and accurate long cantilever box girder calculation model suitable for practical engineering design. By extracting the model of the reaction and the typical cross section stress comparison analysis showed that, compared with single beam, grillage, entity unit model method, plate unit for counterforce size closest to the entity model of the reaction force and horizontal stress change trend was almost consistent with the entity model, more can intuitively reflect the space effect of long cantilever concrete box girder. In addition, in order to ensure the structural safety of the long cantilever concrete box girder, the stress distribution difference of the plate element model in different parts and different states, and the effect of different degrees of transverse prestress on the long cantilever section were studied. The results showed that the shear lag effect at the long cantilever of box girder was very obvious. When the application of transverse prestress was effectively improved the stress of the roof and ensured the safety of the beam.

long cantilever；box girder；unit model；force analysis

2021-10-15

国家自然科学基金项目“参与方个体视角下大型工程项目融资风险动态评价体系研究”（71471094）；山东省自然科学基金项目“基于生态学的大型工程项目融资风险管理体系研究”（ZR2011GL021）；青岛市社科规划项目 “青岛城市基础设施投融资体制创新研究”（QDSKL100403）

刘璐（1995-），女，河南许昌人，助理工程师，硕士，主要从事建筑与土木工程研究，1078222621@qq.com。

U441

A

1007-984X(2022)03-0048-09