第一性原理计算Ti3 GeC2-β相材料的晶格动力学与热力学性质*
2022-06-14刘玉坤张钰莹朱春城
魏 巍,刘玉坤,张钰莹,朱春城
(哈尔滨师范大学)
0 引言
三元层状陶瓷具有金属和陶瓷的双重特性,随着模拟计算领域的广泛研究,包括与材料相关的电子结构和热力学性质的研究,也逐渐成为材料研究的热点[1-5]. MAX 相材料中211 相材料在实验中合成较多,所以以211 相材料为研究的计算也较多.因此,该文采用计算机模拟的方法对MAX相中的312 相的Ti3GeC2-β 材料的声子态密度、声子谱、弹性性质和热力学性质进行理论研究.对于MAX 相材料,其电子结构、晶格动力学和热力学性质决定了它所具有的性能.因此,对其电子结构、晶格动力学和热力学性质的研究对于新型三元陶瓷的开发和实际应用具有深远意义,并发挥着重要的作用.因此,该文采用密度泛函理论的第一性原理计算方法,对Ti3GeC2-β材料的晶格动力学和热力学性质进行了研究和计算.
1 计算方法及理论模型
1.1 计算方法
该文基于Materials Studio 8. 0 软件中的CASTEP模块[6],用于密度泛函理论的第一性原理计算.原子间交换相关效应分别通过局部密度近似(LDA)CA-PZ 函数[7-8]和广义梯度近似(GGA)PBE 函数[9]近似,确定平面波的截断能Ecut=450 eV,布里渊区K点值为12 ×12 ×2.
1.2 理论模型
MAX材料Ti3GeC2-β相的空间结构为六方晶系,空间群P63/mmc(编号194),晶格参数为a =0.299 nm,c =1.847 nm,在Wyckoff 的位置中,钛原子位于2a(0,0,0),4f(2/3,1/3,0.129);锗原子位于2b(2/3,1/3,1/4);碳原子位于(1/3,2/3,0.068).
2 结果与讨论
2.1 晶格动力学性质
该节计算了Ti3GeC2-β 相材料的声子色散曲线和声子态密度,计算结果如图1 和图2 所示.声子态密度[10]和声子色散谱[11]可用于判断Ti3GeC2-β相材料是否具有本征稳定性,还可在此计算基础上算出该材料的热力学性质[12].图1表明Ti3GeC2-β 相的材料存在声子带隙,但图中声子散射频率在0 以下,出现了虚频.说明了Ti3GeC2-β相材料在晶格动力学上不具有本征稳定性,这也解释了在实验中并无Ti3GeC2-β相材料的固体合成.后续力学稳定性判断结果也是如此.声子态密度的峰可以与声子色散谱中平缓的带一一对应,表明Ti3GeC2-β 相材料表现出局域化特征.图2 中可以发现,声子频率在G点附近光学分支是不同的,表明Ti3GeC2-β 相材料中除共价键外还存在离子键[13].声子态密度图中的两个最高峰值分别对应于与H-K 和M-L两个区间平面.在图2 中,18THz处的峰值最高,表明此处声子态密度最大,晶格振动最强.
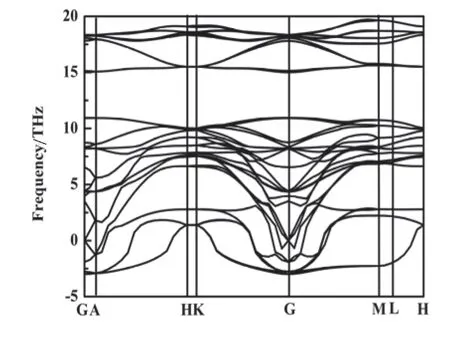
图1 Ti3GeC2-β声子态密度

图2 Ti3GeC2-β声子色散曲线
2.2 弹性性质
该节利用CASTEP 代码包对Ti3GeC2-β 相材料进行几何结构优化后并计算Ti3GeC2-β 相材料的相关弹性常数,结果见表1. Ti3GeC2-β相材料为六方晶系,通过计算出的弹性常数来判断Ti3GeC2-β 的力学稳定性.根据Born 提出的六方晶系的力学稳定性需满足以下关系[14]:
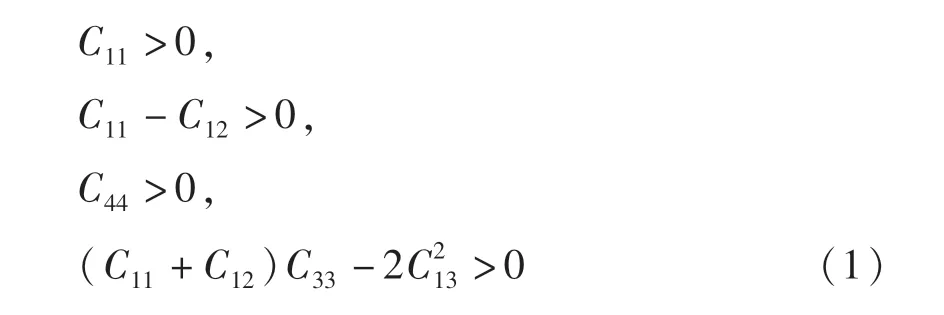
Ti3GeC2-β 相材料的弹性常数C11> 0,C11-C12=197.9 >0,C44=-85.9 <0,(C11+C12)C33-2C213<0;可以判断Ti3GeC2-β相材料在力学上不能够稳定存在,Ti3GeC2-β相材料不具备力学稳定性.根据计算得到的弹性常数,利用Vogit-Reuss-Hill[15]近似法计算出Ti3GeC2-β相材料的体积模量B和剪切模量G,公式如下:

Pugh[16]的模量比用来判断材料的延展性和脆性,根据表中数据计算出B/G =2.26 >1.75,所以Ti3GeC2-β 相材料为延展性材料.表1 中数据可知Ti3GeC2-β 相材料的泊松比σ =0.426,在-1 和0.5 之间,说明Ti3GeC2-β相材料被压缩的弹性性能一般.与此同时,还可以从表1 中看出Ti3GeC2-β 相材料抗体积变化能力强,所以B 值较大,但G 值较小,原子间有比较明显的价键方向.晶体的材料拉伸弹性E值也较高.综上所述,Ti3GeC2-β相材料具有延展性,弹性性能一般,但其中抗体积形变能力较好.

表1 Ti3GeC2-β相材料的相关弹性系数
2.3 热力学性质
计算得出的声子色散可用于计算Ti3GeC2-β相材料在0 ~1000 K范围内的熵、焓、自由能、德拜温度和热容的关系曲线.
图3 所示,蓝色曲线是Ti3GeC2-β 相材料的熵S与温度T相乘所得到的结果.随着温度的升高,粒子的动能增加并且内能增加.粒子无序性增加,因此熵也增加,所以TS 乘积也增加.黑色曲线表示焓H与温度T之间的关系.当温度升高时,系统的焓H 随温度升高而升高.红色曲线是自由能F 随温度T 变化的关系图.可用F =U-TS代表自由能,其中U 是系统的内能.随着温度升高,内能和熵增加,但TS 增加,速度高于U增加的速度,所以F随着T的增加而减少.
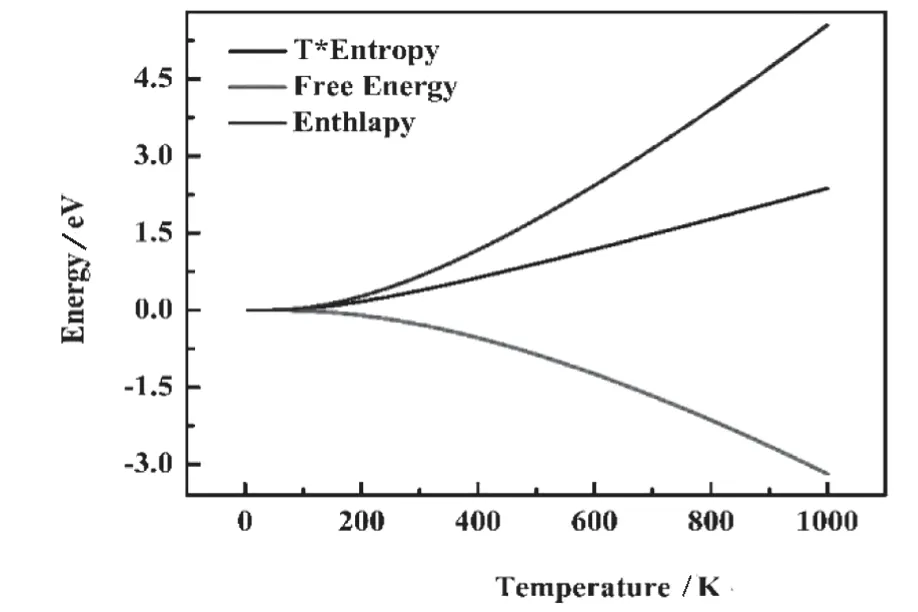
图3 Ti3GeC2-β能量随温度变化曲线
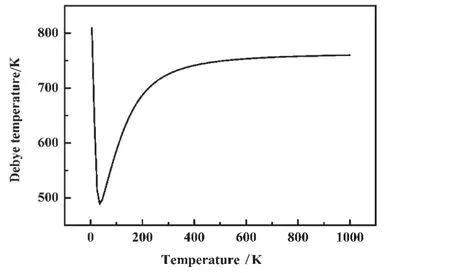
图4 Ti3GeC2-β的德拜温度的变化曲线
德拜温度可以从物理角度反映原子间键的强度.德拜温度越高,原子间作用力越大,熔点越高.所以不同物体的德拜温度是不同的.如图5所示,当温度远低于德拜温度时,等容热容[17]服从量子定律,随温度降低而减小;当温度高于德拜温度时,等容热容Cv服从Duro-Petit 定律[18],即是一个与材料物质无关的常数(Cv=3R),等容热容Cv是一个常数.
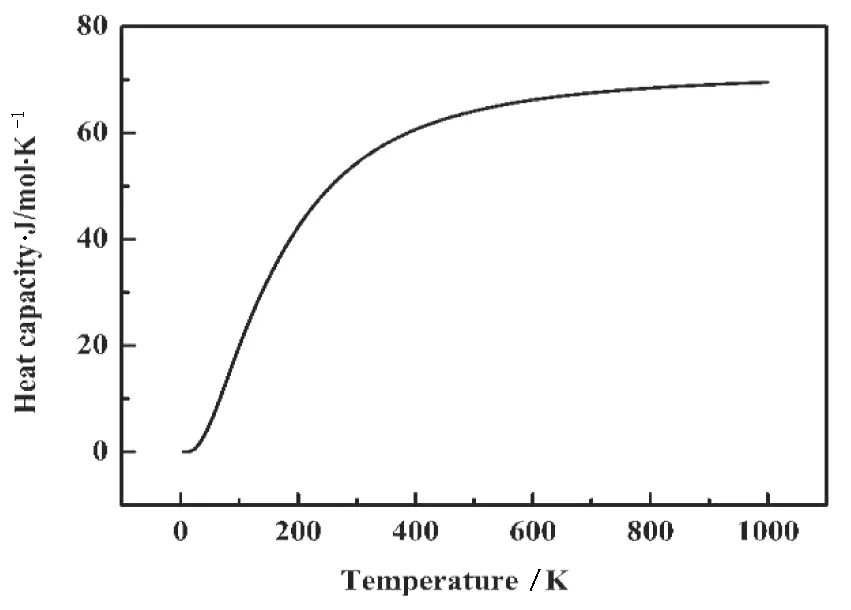
图5 Ti3GeC2-β热容随温度变化的曲线
3 结论
(1)对弹性性质的计算结果分析表明:Ti3GeC2-β相材料不具有力学稳定性,具有延展性;但是压缩弹性一般,其余弹性模量都较好.
(2)对晶格动力学性质的计算结果分析表明:Ti3GeC2-β相材料的声子色散曲线图中有虚频出现,不具有本征稳定性;在18THz 此处晶格振动最强.
(3)对热力学性质的计算结果分析表明:Ti3GeC2-β相材料的熵和焓随温度的升高而增加,自由能则随之减少;定容热容随温度的升高开始改变较快,随后逐渐平缓,直至趋近于常数3R.Ti3GeC2-β 相材料的德拜温度虽然随温度变化,但是在任何情况下都服从热力学第三定律和杜隆-珀替定律和拜T3定律.
