青藏铁路路基粗颗粒填料动力特性和安定性行为研究

王庆志， 周志伟， 张淑娟

（1.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州730000； 2.中国科学院大学，北京100049）

0 引言

近年来在“一带一路”倡议下，我国寒区高速铁路建设正如火如荼地展开［1］。对于寒区高速铁路工程的合理设计、安全运维而言，高速铁路在复杂热力环境下长期服役性和稳定性的保障是首要的考虑要素，而长期稳定性受到路基填料层在交通荷载下动力响应的制约。对于高纬度高海拔寒区铁路而言，冻融条件、颗粒级配、循环热-力路径又主要影响着不同路基填料层的累积变形响应过程。由于复杂热-力环境下路基填料层的不均匀沉降诱发高速铁路多种路面与路基病害，如横向裂缝、路基边坡开裂及铁轨变形等［2］。因此迫切需要深入理解不同类型路基填料以及填料层结构在高速交通荷载作用下的累积变形演化特征以及对复杂热力条件的定量响应规律。

高速铁路路基填料在交通循环荷载下的累积变形演化特征可依次归类为塑性安定、塑性蠕变及加速坍塌破坏三种类型［3-4］，而对这三种变形类型的准确判定（安定性评估）对于路基的合理设计、安全运营、经济维护起到至关重要的作用。基于热/力载荷的水平、类型、循环次数来判定材料/结构长期累积变形量是否满足工程允许极限值的方法称为安定性评估方法，在这方面国内外学者开展了一些研究。廖化荣等［5］分析了红黏土在循环动荷载下累积塑性变形的发展规律及影响因素，并界定了其安定界限；肖军华［6］通过动三轴试验研究了长期动荷载下路基压实粉土的临界动应力和回弹应变水平；董城等［7］开展系列动三轴试验，得到不同含水率和压实度下粉土累积塑性应变的划分标准；Qian 等［8］利用动态空心圆柱仪开展心型应力路径下固结不排水三轴试验，并提出一种基于有效应力比定义黏土安定性行为边界的新方法；Xiao 等［9］基于激光扫描试验技术和离散元数值模拟，研究循环动应力幅值、围压及频率对道砟材料累积塑性形变及安定性行为的影响。从路基工程的实际稳定性来考虑，只有塑性安定及轻微的塑性蠕变两种累积塑性变形类型可以允许发生，加速坍塌破坏类型必须严格杜绝发生。然而如何有效地利用安定性评估方法来准确预测和判定路基颗粒材料累积塑性变形趋势，并明确各类累积变形行为的临界动应力与塑性应变水平，成为当前路基工程中亟待解决的重要问题。

现今常用的路基安定性评估准则有两类：（1）德累斯顿工业大学的Werkmeister-准则［10］，Rahman等［11］基于该准则采用多级循环加载三轴试验并提出考虑应力路径影响的松散颗粒材料累积塑性应变的预测模型；Xiao 等［12］开展了恒围压和动围压三轴试验分类，研究了在长期车辆动载条件下承受不同应力路径、动应力幅值及应力比的路基填料层和底基层填料的累积塑性变形规律。（2）香港理工大学的陈-准则［13］，郑可扬等［14］基于陈-准则和Savitzky-Golay 滤波法，提出了一种新的累积塑性变形行为划分方法。以上研究中两类安定性评估准则主要应用于常温条件下的路基颗粒填料及其填料层结构，而现有考虑冻结负温以及冻融过程下路基安定性行为的研究则相对较少，中国科学院西北生态环境资源研究院的马巍课题组提出了一种针对寒区冻结路基填料的安定性评估准则（马-准则）［15］，并验证和判定了该准则在兰-新高铁冻结路基填土累积变形过程方面的适用性和准确性。

本文基于MTS-810 振动低温三轴材料试验机，采用分级循环加载方式对青藏铁路冻结路基粗颗粒填料进行试验研究。分析不同冻结负温、粗粒级配及循环应力路径下冻结路基填料累积塑性变形和回弹变形演化特征，旨在通过试验确定Werkmeister-准则、陈-准则及马-准则三类安定性评估准则对路基填料在冻结低温条件下的适用性，以期在考虑冻结和冻融条件过程下为寒区高速铁路路基填料层的合理设计、安全运营及经济维护提供重要基础数据和关键理论支撑。

1 试验概况

1.1 试验设备

试验所采用的MTS-810 振动低温三轴材料试验机被很多学者广泛应用于冻土静、动力学测试中［16］。该试验机的技术指标如下：最大轴向负荷为100 kN；围压可控范围为0～20 MPa，围压控制系统使用的加压液体为10号航空液压油；轴向位移范围为-85～85 cm；轴向加载频率范围为0～20 Hz；围压加载频率范围为0～5 Hz；正常运行环境温度范围为-30 ℃～20 ℃；冷却系统中使用的制冷介质为冷冻液，其冰点为-40 ℃。

1.2 模具尺寸

在三轴试验试样尺寸的确定中，必须考虑到MTS-810 低温三轴压力室尺寸的限制，使试样与压力室内壁保持足量空间，确保压力室温度可控的前提下，参考常温条件下路基填料试样尺寸100 mm×200 mm（直径×高度）［17］使模具尽量容纳大颗粒填料，试验中采用圆柱形试样尺寸为75 mm×150 mm，模具内径尺寸为75 mm×220 mm，如图1所示。

图1 试样及模具尺寸Fig.1 Sample and mould sizes

1.3 试验材料

试验采用了粗颗粒填料试样，试样由细粒土（所有颗粒粒径小于2 mm）和粗颗粒填料混合压实制备而成。细粒土为青藏高原砂质粉土，取自青藏铁路北麓河沿线段，其基本物理参数如表1 所示。粗颗粒填料取自广西南宁，根据《铁路工程土工试验规程》（TB 10102—2004）［18］的土工测试要求，粒径分布范围为2～9 mm，如图2（a）所示。

表1 基本物理性质指标Table 1 Basic physical indices

在试样制备过程中，采用了与实际工程相同的土壤压实度，使先期固结压力过大，考虑到此时粗颗粒含量较多试样易发生颗粒破碎现象及难以压实成型的问题，试验选取了6 组粗颗粒与细粒土的质量配比，对应粗颗粒含量分别为5%、10%、15%、20%、25%和30%，如图2（b）所示。图2（c）为粗颗粒含量为30%的级配土粒径分布曲线，该图中7∶3 表示细颗粒土含量为70%，粗颗粒含量为30%，其中1∶1∶1、3∶0∶0、0∶3∶0 和0∶0∶3 分别代表粒径为6～9 mm、4～6 mm和2～4 mm颗粒的质量比。

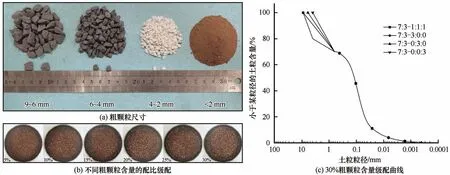
图2 试样材料Fig.2 Sample material［coarse particle sizes（a），mixture fillers with different coarse particle contents（b），particle distribution curves with 30%coarse particle content（c）］

1.4 试验方案

在实际交通荷载作用下，任一路基断面上填料的应力状态随车轮移动产生主应力大小变化以及方向旋转，并在下一车轮作用下重复这一过程。室内试验中可采用轴向和径向双向循环加载过程来实现土样多轴循环应力状态，在p-q应力平面下（或主应力平面下）以应力加载路径k=qampl/pampl=1.5（k为应力路径斜率值，qampl和pampl分别为每次循环加载下的偏应力幅值与平均主应力幅值）、偏应力幅值为300 kPa 时的加载条件为例，加载波形如图3（a）所示。此外，我国现行高速铁路平均运行时速为250～350 km·h-1，列车单节车厢长度约为25 m，根据上述两工程指标计算出高速列车引起的动载频率为2.78～3.89 Hz，而青藏铁路在多年冻土区的平均运营时速是120 km·h-1，对应车载动荷频率为1.33 Hz，为保证实验结果对工程的可靠性，试验取循环加载频率为1.50 Hz；考虑到实际高速铁路路基动应力水平与现场路基侧约束条件，多级循环加载试验中偏应力幅值取50、100、150、200、300 kPa 共5 级，多级循环加载试验每一级偏应力幅值循环加载次数为20 000次，围压为100 kPa（恒围压）和400 kPa（动围压）。详细的加载程序和试验条件如图3（b）和表2所示。

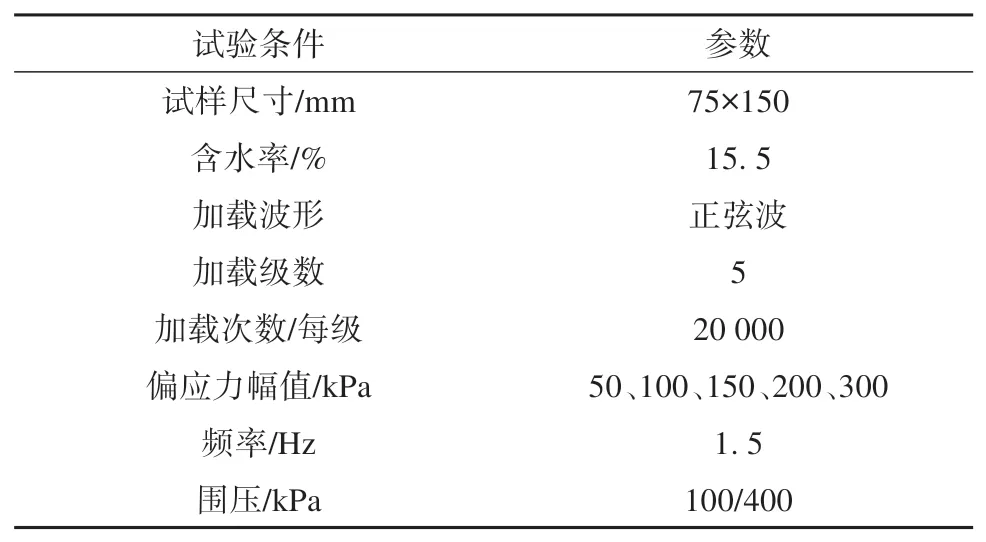
表2 试验条件Table 2 Cyclic loading conditions

试验采用恒围压（constant confining pressure）和动围压（variable confining pressure）两类循环动力学试验。在CCP 试验方案中设置温度组，有-2 ℃、-3 ℃、-4 ℃和-6 ℃；不同细粒土与粗颗粒含量之比在9.5∶0.5 至7∶3 范围内；三种不同粒径［依次为（6～9 mm）∶（4～6 mm）∶（2～4 mm）］粗颗粒含量之比包括1∶1∶1、3∶0∶0、0∶3∶0、0∶0∶3四种。在VCP试验方案中设置了k=1.5、3.0、6.0、等p、-3.0 和-1.5 六条循环应力加载路径，如图3（c）所示。恒围压与动围压试验方案如表3 所示。以恒围压条件下CCP-1与动围压条件下VCP-1-6为例，循环三轴加载参数设置如表4所示。冻结试样完成循环加载试验后的形状如图3（d）所示。

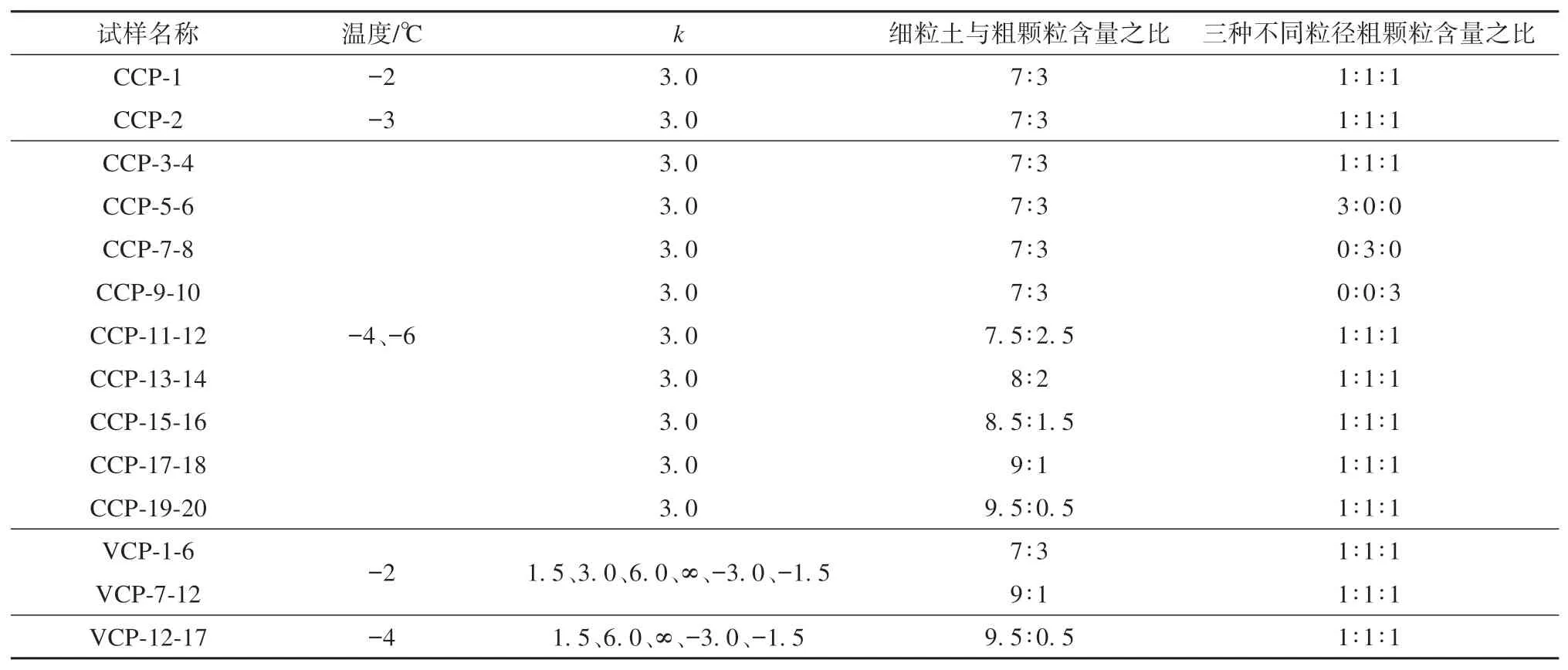
表3 试验方案Table 3 Particle distribution conditions

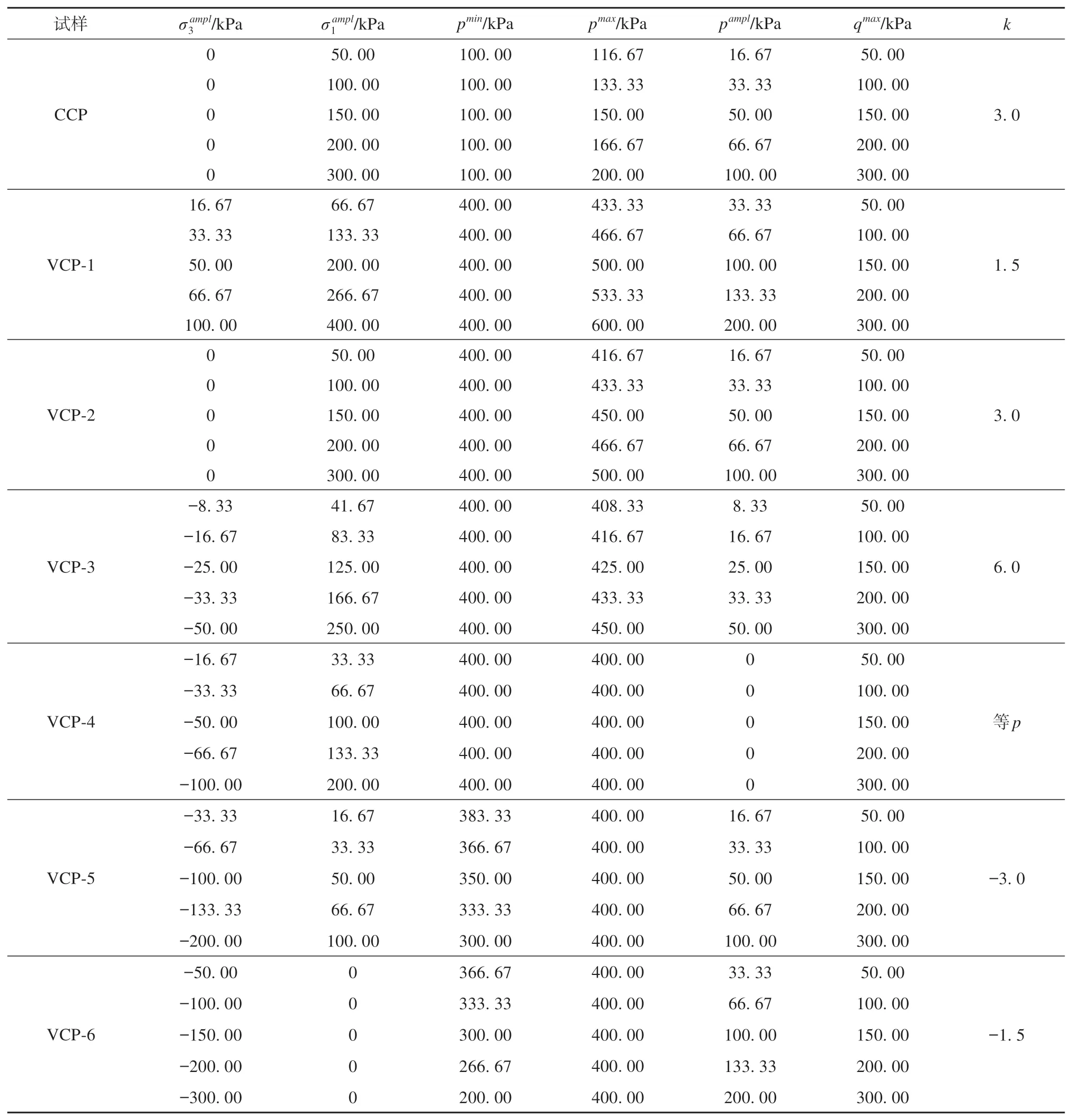
表4 三轴循环测试条件Table 4 Triaxial testing programs

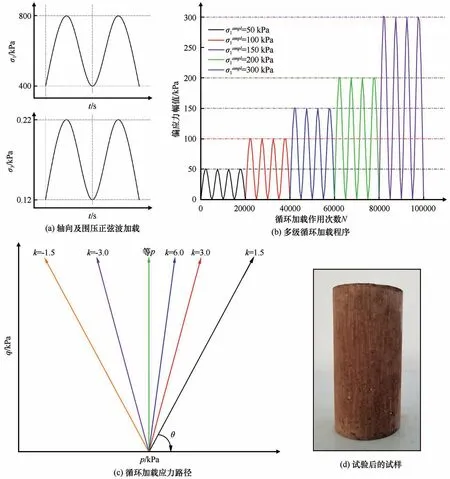
图3 试验加载Fig.3 Test loading［cyclic pattern of axial loading and confining pressure（a），multi-stage cyclic programs（b），cyclic stress paths（c），tested samples（d）］

2 试验结果

2.1 冻结路基填料的轴向累积塑性应变

图4表明了在CCP 和VCP 条件下轴向累积塑性应变与循环加载作用次数的关系。冻结路基填料在任一偏应力幅值状态下轴向累积塑性应变均随着循环加载作用次数的增加而增大，并随偏应力幅值的增大而明显增大。除图4（c）中等p、k=-3.0及k=-1.5的应力加载路径外，其余所有变化曲线均存有类似的演化趋势，即同一偏应力幅值加载作用下轴向累积塑性应变于最初的循环动荷载中急剧增大，并随循环次数的增加最终趋于稳定，且在下一偏应力幅值状态下重复这一过程；根据这一演化趋势，明显可以将相同偏应力幅值作用下轴向累积塑性应变的变化曲线划分为后循环压实阶段与二次循环变形两个阶段，而对于不同偏应力幅值、冻结负温、粗粒级配及应力路径下两阶段的划分方式并不完全相同，应依据不同的安定性准则合理确定两阶段间过渡期的分界点。

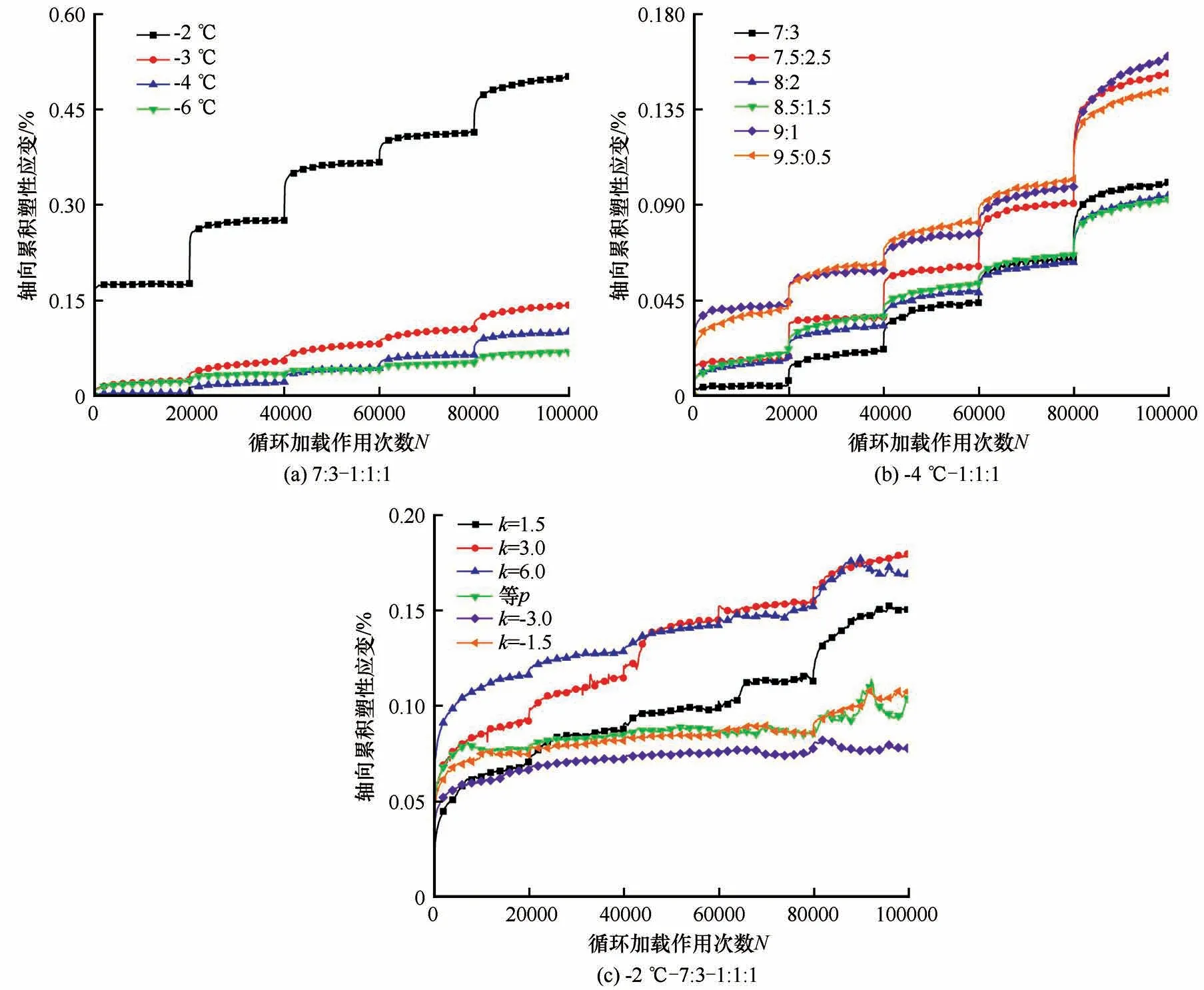
图4 冻结路基填料轴向累积塑性应变变化Fig.4 Axial cumulative plastic strain of frozen subgrade fillers［7∶3-1∶1∶1（a），-4 ℃-1∶1∶1（b），-2 ℃-7∶3-1∶1∶1（c）］

2.2 冻结路基填料的体变

图5表明了在CCP 和VCP 条件下体变与循环加载作用次数的关系。CCP 试验中冻结路基填料在任一偏应力幅值状态下体变与循环加载作用次数成正相关，并随偏应力幅值的增大而明显增大；VCP 试验中不同应力路径下的体变随循环加载作用次数的发展趋势有所不同，在冻结负温和粗粒级配一致的情况下，其体变受不同应力加载路径中围压和轴向压力的耦合作用影响显著，且于VCP 试验中得到的体变值比CCP 试验中的体变基本小一个数量级。这主要是由于循环围压对径向变形的抑制作用跟循环轴向应力引起的循环体积变形同步。在图5（a）、（b）中与轴向累积塑性应变的变化曲线不同，体变曲线不存在两阶段的演化趋势，仅在qampl=50 kPa的偏应力作用下其体变快速发展，且随循环次数的增加体变率逐渐减小，并在其余偏应力幅值状态下基本保持恒定。

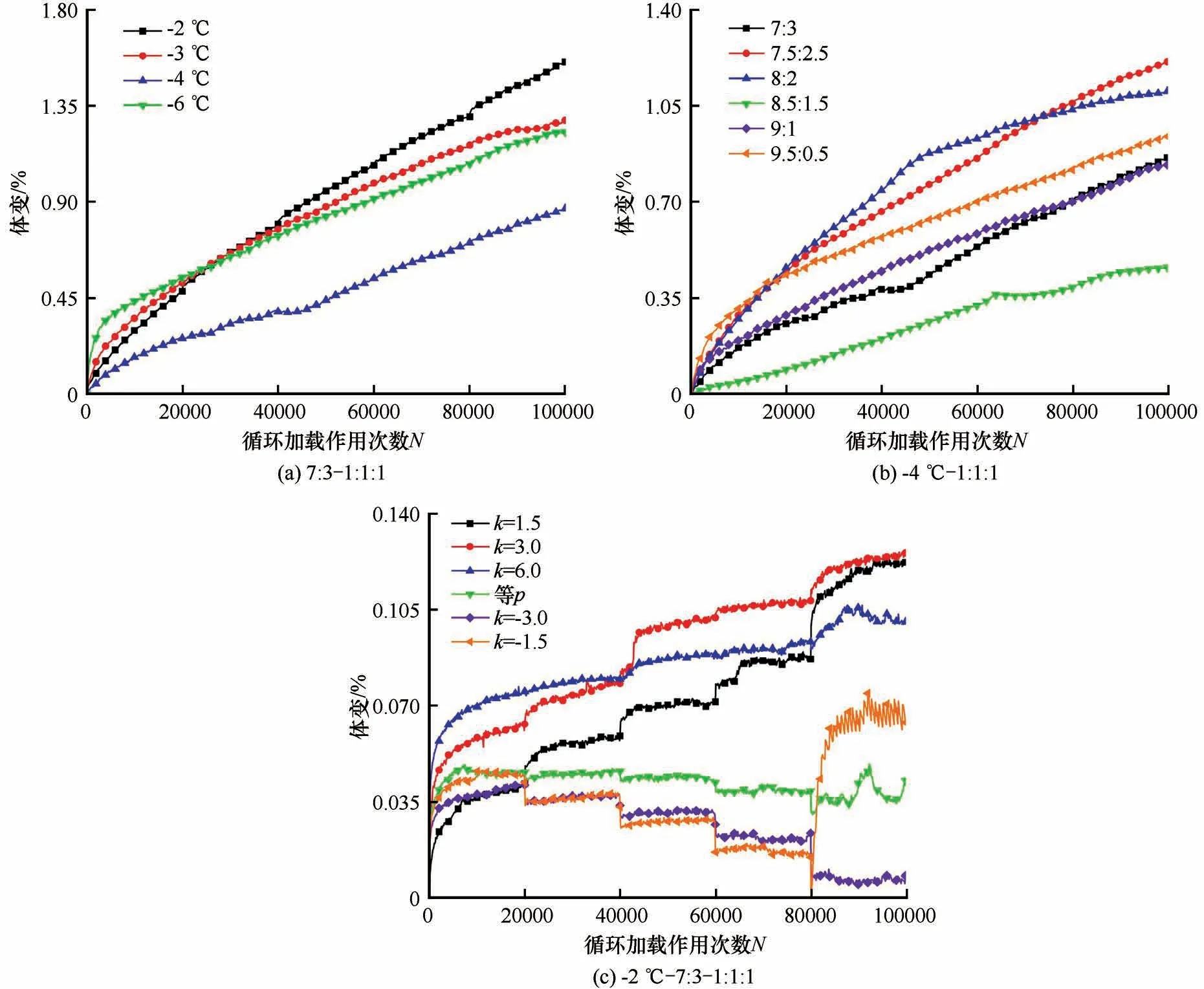
图5 冻结路基填料体变变化Fig.5 Volumetric strain of frozen subgrade fillers［7∶3-1∶1∶1（a），-4 ℃-1∶1∶1（b），-2 ℃-7∶3-1∶1∶1（c）］

2.3 冻结路基填料的轴向累积塑性应变率

图6表明了在CCP 和VCP 条件下轴向累积塑性应变率与轴向累积塑性应变的关系。本文采用每500次循环加载作用下平均塑性应变增量来表征冻结路基填料的轴向累积塑性应变率。冻结路基填料在任一偏应力幅值状态下轴向累积塑性应变率与塑性应变成负相关关系，而在相同轴向累积塑性应变率条件下其塑性应变仅随偏应力幅值的增大而增大，且与冻结负温、粗粒级配及应力路径无直接联系，这表明循环动荷载作用下偏应力幅值对其轴向累积塑性应变率起主导作用；此外于VCP 试验中得到的轴向累积塑性应变率与CCP 试验中的应变率在数值上无明显差距。

图6 冻结路基填料轴向累积塑性应变率变化Fig.6 Axial cumulative plastic strain-rate of frozen subgrade fillers［7∶3-1∶1∶1（a），-4 ℃-1∶1∶1（b），-2 ℃-7∶3-1∶1∶1（c）］

2.4 冻结路基填料的回弹模量

图7表明了在CCP 和VCP 条件下回弹模量与循环加载作用次数的关系。本文采用每500 次循环加载作用下回弹模量的平均值来绘制这一变化曲线。冻结路基填料在qampl=50、100 kPa 的偏应力幅值状态下部分回弹模量曲线随着循环加载作用次数的增加而增大，其余曲线和qampl=150、200、300 kPa 的偏应力幅值状态下回弹模量随着循环加载作用次数的增加而减小，且所有曲线最终趋于稳定；回弹模量曲线同样存在两阶段的演化趋势，即从初始增长/减小阶段过渡至稳态阶段，其中初始阶段的回弹模量是否增长或者减小与试样的先期固结压力有关，当试样处于欠固结状态下，曲线呈增长发展至稳定趋势，而试样处于超固结状态下，曲线呈减小发展至稳定趋势。

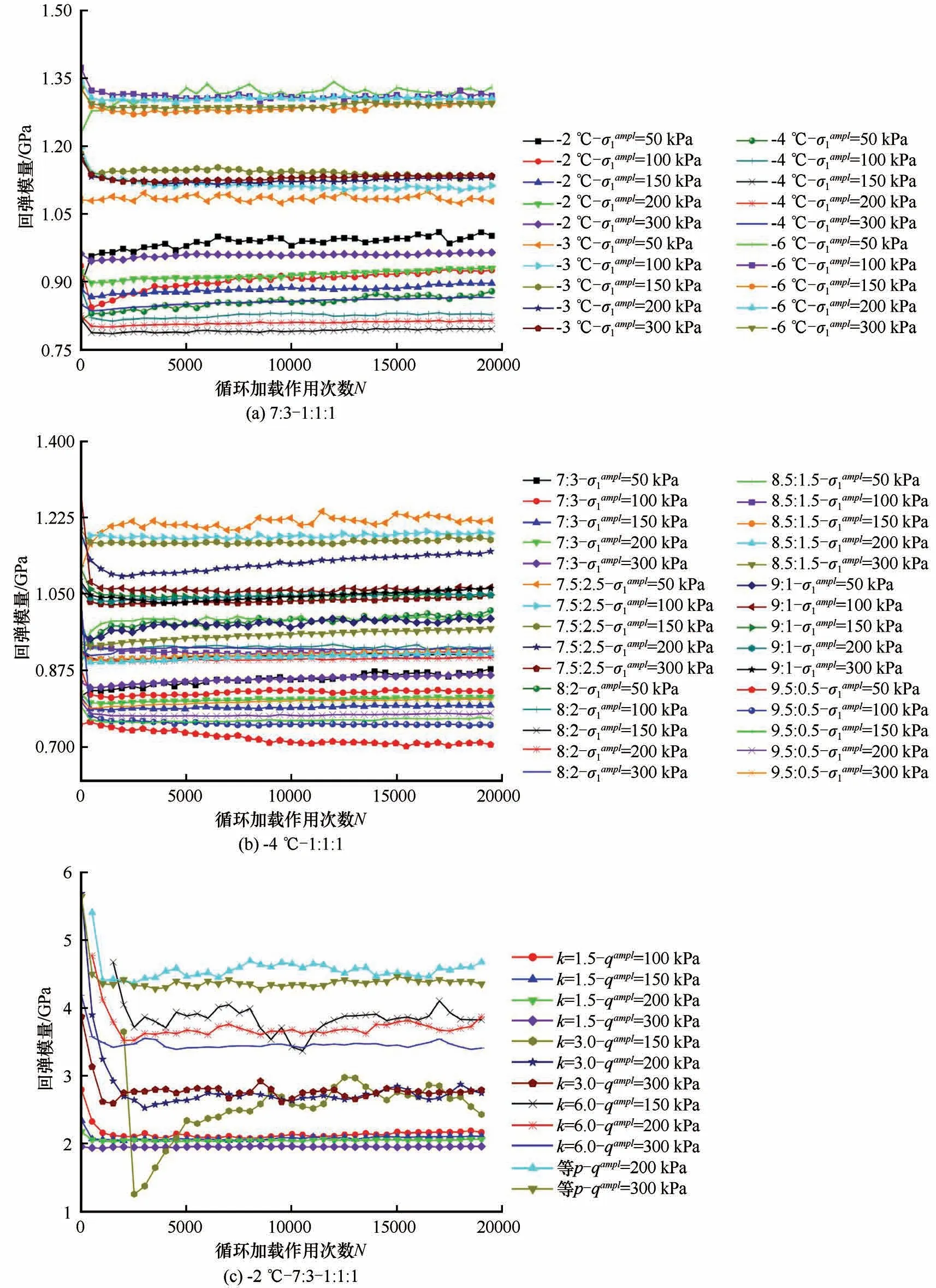
图7 冻结路基填料回弹模量变化Fig.7 Resilient modulus of frozen subgrade fillers［7∶3-1∶1∶1（a），-4 ℃-1∶1∶1（b），-2 ℃-7∶3-1∶1∶1（c）］

此外于VCP 试验中得到的回弹模量值明显大于CCP试验中的回弹模量，且VCP试验中的回弹模量曲线进入稳态阶段相对滞后，这种现象在k=3.0和k=6.0 的应力加载路径下最为显著，这主要是土体回弹行为的物理机制较为复杂，随着应力路径系数的增加轴向应力幅值和围压应力幅值同步增量均增大，随着循环围压幅值的增加，在保持循环偏应力幅值不变的条件下，循环球应力增大引起的回弹变形进一步增大，趋于稳定的过程需要的循环次数也就进一步增大。

3 讨论

3.1 冻结负温对累积塑性变形和回弹变形行为的影响

图8显示了CCP 试验中冻结负温为-2 ℃、-3 ℃、-4 ℃、-6 ℃的测试结果。从图8（a）中可以看出，其轴向累积塑性应变随冻结温度的升高而增大，且冻结温度的影响随偏应力幅值的增加而更明显。冻土是由矿物骨架、冰、未冻水及气体组成的复杂的多相多成分体系，冻结温度越低，矿物颗粒骨架之间未冻的液态水冻结成固态冰，冰晶数量逐渐增多且强度逐渐增强，在抵抗外部动荷载过程中发挥着和矿物颗粒骨架相同的作用；与未冻的液态水相比，冻结试样中的固态冰在矿物颗粒骨架间起到不可忽视的胶结作用，使土体整体的刚度得到强化，故循环加载过程中的冻结温度越低，抵抗产生塑性应变的能力越强。

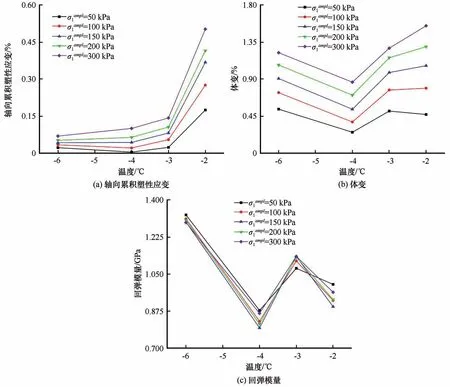
图8 不同偏应力幅值条件下轴向累积塑性应变、体变、回弹模量与冻结负温的变化曲线（7∶3-1∶1∶1）Fig.8 Axial cumulative plastic strain，volumetric strain，resilient modulus versus freezing negative temperature under different conditions of deviator stress amplitude（7∶3-1∶1∶1）［axial cumulative plastic strain（a），volumetric strain（b），resilient modulus（c）］

从图8（b）中可以看出，其体变随冻结温度的降低呈先减小后增大的变化趋势。当冻结温度从-2 ℃降低到-3 ℃时，试样的体变减小，且降幅随着偏应力幅值的增加更加显著；在-2 ℃下试样中还有部分未冻的液态水，冰晶与固体矿物骨架间的胶结能力较弱，此时粗颗粒材料更易移动错位及滑动，宏观表现为体变的快速累积，而在-3 ℃下试样液态水近乎完全冻结成固态冰，同时冻结温度降低到-4 ℃时，胶结冰的数量和作用进一步增大；当冻结温度降低至-6 ℃时，固态冰与固体矿物骨架间具有较大的胶结作用，粗颗粒材料更易在循环动荷载作用下产生破碎现象，从而填充试样间的孔隙。

从图8（c）中可以看出，其回弹模量随冻结温度的升高呈先减小后增大再减小的变化趋势。回弹模量减小的原因与其体变增大的原因基本一致，-6 ℃的冻结温度下受循环动荷载作用试样中的粗颗粒材料破碎，回弹变形大大降低；-4 ℃的冻结温度下试样的强度较大但尚不能达到粗颗粒材料的硬度水平，回弹变形达到最大；而后随着冻结温度的升高，冰晶数量逐渐减少，其被压裂、压融过程对土性影响的物理机制较为复杂，回弹变形呈现出先减小后增大的趋势。

3.2 粗粒级配对累积塑性变形和回弹变形行为的影响

图9显示了CCP试验中所添加的粗颗粒含量为5%、10%、15%、20%、25%、30%的测试结果。从图9（a）中可以看出，在-4 ℃的冻结温度下轴向累积塑性应变随粗颗粒含量的增大而减小。冻结试样中所添加的粗颗粒含量越多，成分中细粒土含量越少，在循环动荷载作用下土体矿物骨架间产生较大的相对滑移，且相互挤压、填充作用进一步增强，宏观表现为塑性应变的急剧增大，直至应力达到峰值发生剪切破坏，此时试样强度由粗细料共同作用逐渐向由固体矿物骨架及冰晶共同作用转变，故冻结试样中含有的粗颗粒越多，抵抗产生塑性应变的能力越强。

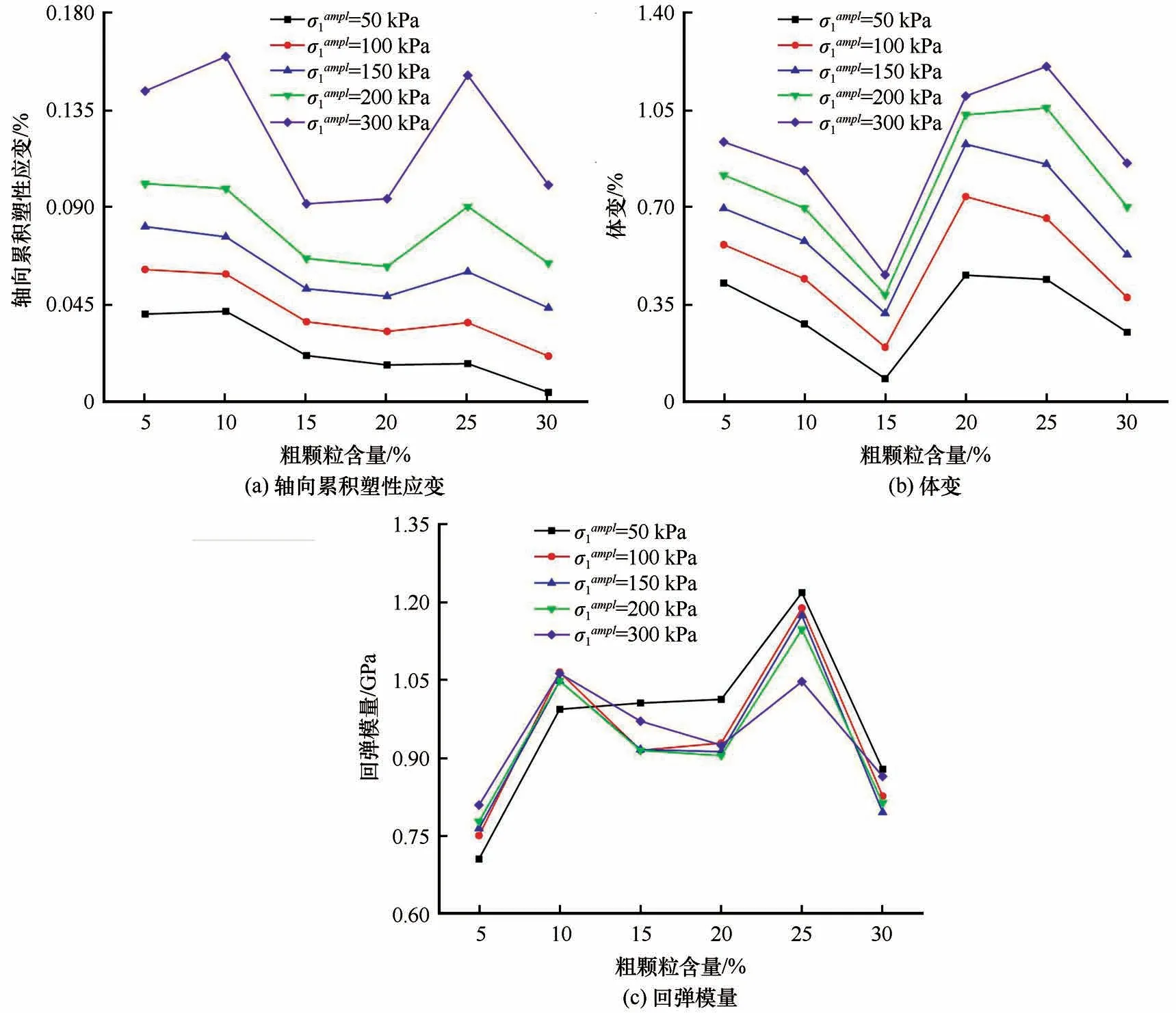
图9 不同偏应力幅值条件下轴向累积塑性应变、体变、回弹模量与粗颗粒含量的变化曲线（-4 ℃-1∶1∶1）Fig.9 Axial cumulative plastic strain，volumetric strain，resilient modulus versus coarse particle content under different conditions of deviator stress amplitude（-4 ℃-1∶1∶1）［axial cumulative plastic strain（a），volumetric strain（b），resilient modulus（c）］

从图9（b）中可以看出，在-4 ℃的冻结温度下体变随粗颗粒含量的增大先减小后增大再减小；第一转折点均发生于粗颗粒含量为15%的试样，即取得体变最小值，而随着偏应力幅值的增加，第二转折点由粗颗粒含量20%的试样逐渐向25%的试样转变。从图9（c）中可以看出，在-4 ℃的冻结温度下回弹模量于10%、25%的粗颗粒含量存在上升趋势，于15%、20%、30%的粗颗粒含量存在下降趋势，且两次上升幅值基本接近相同，同时于粗颗粒含量5%和25%的试样分别取得回弹模量最小值与最大值。

3.3 应力路径对累积塑性变形的影响

图10显示了VCP 试验中应力加载路径为k=1.5、k=3.0、k=6.0、等p、k=-3.0 及k=-1.5 的测试结果。从图10（a）中可以看出，粗颗粒含量30%冻结试样的轴向累积塑性应变均与偏应力幅值呈正相关关系，且随应力加载路径的改变呈先增大后减小再增大的变化趋势。在冻结负温和粗粒级配一致的情况下，不同应力路径的轴向累积塑性应变受围压和轴向压力的耦合作用影响显著：围压减小时，径向约束较小，有利于试样塑性应变的累积，围压增大时，径向约束较大，增强其抵抗塑性应变的能力，而轴向压力的增大与减小则与塑性应变的累积存在直接联系。在低偏应力幅值下塑性应变于k=6.0 的应力加载路径中取最大值，且随着偏应力幅值的增加逐渐向k=3.0 的应力加载路径转变，而最小值仅发生在k=-3.0的应力加载路径中。

从图10（b）中可以看出，粗颗粒含量30%冻结试样的体变随偏应力幅值的变化趋势受应力加载路径影响显著，即应力路径为k=1.5、k=3.0和k=6.0的体变随偏应力幅值的增加呈上升趋势，应力路径为k=-3.0 和k=-1.5 的体变随偏应力幅值的增加呈下降趋势，而等p应力路径下的体积应变发展基本不受偏应力幅值的影响，这是由于不同应力加载路径下围压和轴向压力的耦合作用致使冻结试样具有不同程度的剪缩性与剪胀性所导致的。

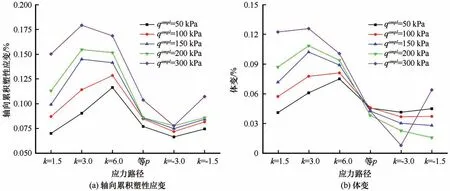
图10 不同偏应力幅值条件下轴向累积塑性应变、体变与应力路径的变化曲线（-2 ℃-7∶3-1∶1∶1）Fig.10 Axial cumulative plastic strain，volumetric strain versus stress path under different conditions of deviator stress amplitude（-2 ℃-7∶3-1∶1∶1）［axial cumulative plastic strain（a），volumetric strain（b）］

3.4 三类安定准则的试验验证

根据Werkmeister-准则，图11 为第3 000 至5 000 次循环动荷载间轴向累积塑性应变增量Δεap，5000- Δεap，3000与偏应力幅值关系曲线。除图11（c）以外，应变增量均随着偏应力幅值的增大而增大。在图11（a）中，试样在-2 ℃的冻结负温下取得各偏应力幅值下应变增量的最大值，即应变增量随冻结温度的升高而增大，同时温度效应与偏应力幅值无明显联系；在偏应力幅值为300 kPa 时，-2 ℃冻结试样的应变增量大于4.5×10-5，达到塑性蠕变范围，而其余试验结果均属于塑性安定。在图11（b）中，试样在粗颗粒含量为5%与10%时取得各偏应力幅值下应变增量的最大值，即粗颗粒含量越小其应变增量越大；试样中粗颗粒含量对应变增量的影响随着偏应力幅值的增加先减小后增大，即200 kPa的偏应力幅值下粗颗粒含量效应最小；仅粗颗粒含量为10%的试样在300 kPa 的偏应力加载下应变增量超过塑性安定界限，达到塑性蠕变范围。在图11（c）中，试样在k=-1.5 的应力路径中取得各偏应力幅值下应变增量的最小值，在k=1.5 和k=3.0 的应力路径中取得应变增量的最大值；在qampl=50 kPa 的动应力下应变增量较大，此时k=1.5、3.0、6.0 应力加载路径下的试样达到塑性蠕变范围，而随偏应力幅值的增加其应变增量呈先减小后增大的趋势，且试验结果基本属于塑性安定。

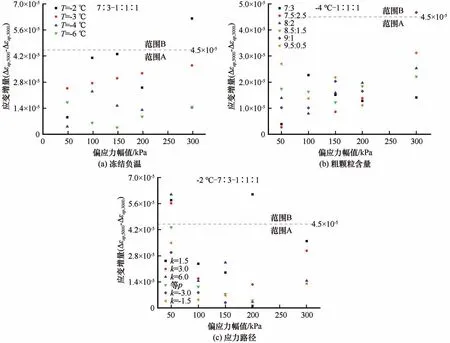
图11 轴向累积塑性应变增量Δεap，5000 - Δεap，3000与偏应力幅值关系曲线Fig.11 The increment of axial cumulative plastic strain Δεap，5000 - Δεap，3000 versus deviator stress amplitude［freezing negative temperature（a），coarse particle content（b），stress path（c）］

根据陈-准则，用后循环压实阶段与二次循环变形阶段拟合直线的交点所对应的循环加载次数来表征两阶段间的边界点，为最大限度地确保试验阶段均处于二次循环变形阶段，将边界点精确至数量级的整数倍，在本文中所有冻结试样均采用1 000 次循环加载作为两阶段边界点，对1 000 次循环动荷载后的塑性应变进行拟合，如图12 所示。图13 为二次循环变形阶段斜率1/as与偏应力幅值关系曲线。可以看出，陈-准则的评估关键参数受各因素的影响规律与Werkmeister-准则基本相似，除图13（c）以外，二次循环变形阶段斜率均随着偏应力幅值的增大而增大，随冻结温度的升高而增加，随粗颗粒含量的降低而递增，同时在k=-1.5 的应力路径中取得各偏应力幅值下的最小值；此外，在陈-准则下得到的安定性评估结果均属于塑性安定范围。

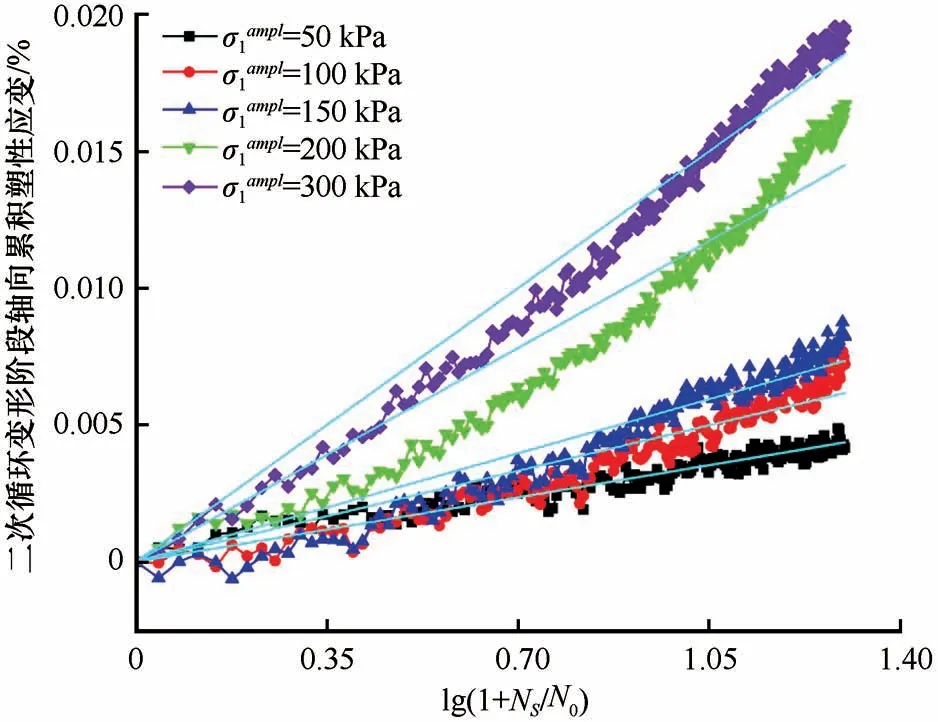
图12 不同偏应力幅值条件下二次循环变形阶段的轴向累积塑性应变特征（-4 ℃-7∶3-3∶0∶0）Fig.12 The features of axial cumulative plastic strain during the second-cycle deformation stage under different conditions of deviator stress amplitude（-4 ℃-7∶3-3∶0∶0）

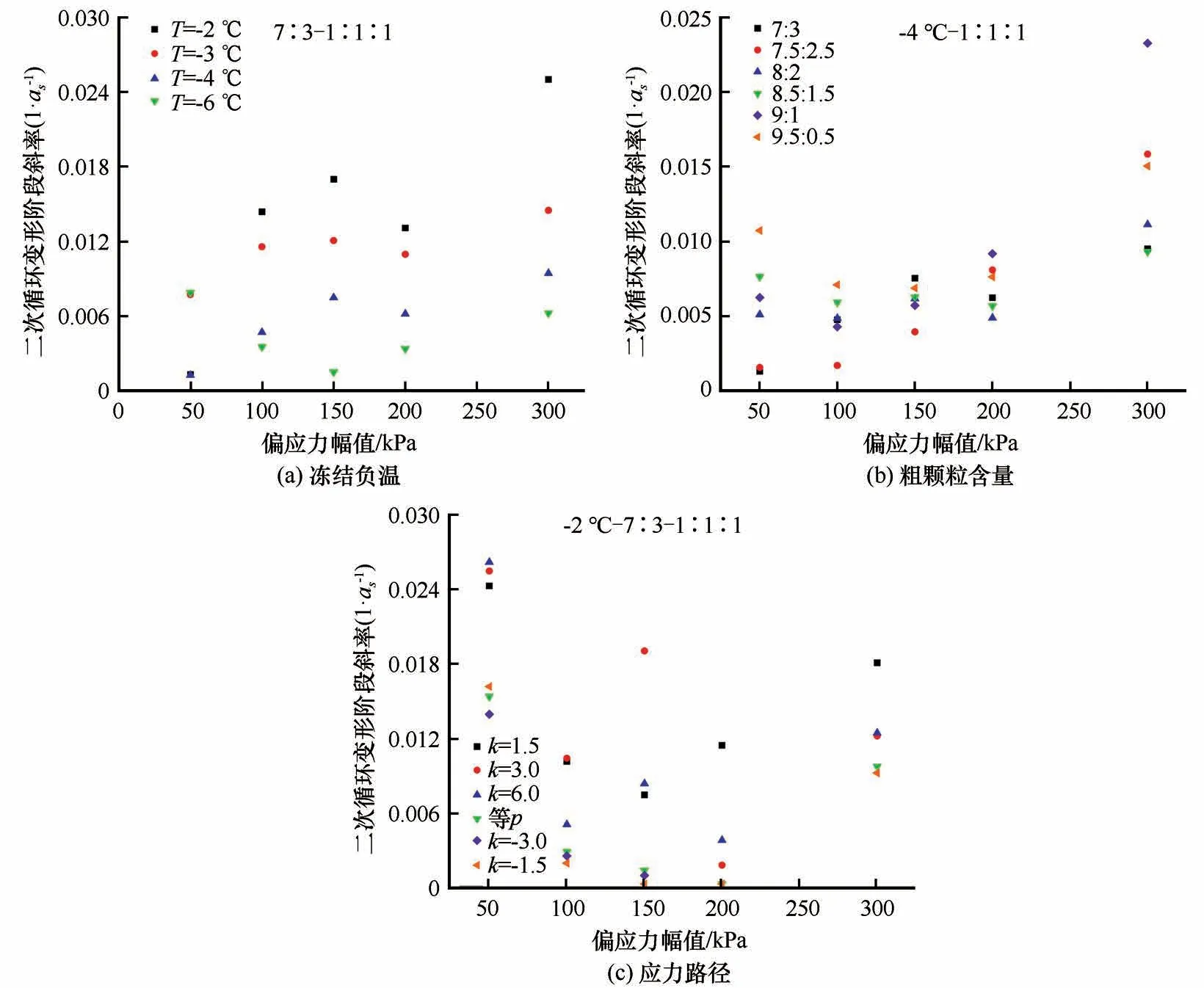
图13 二次循环变形阶段斜率1/as与偏应力幅值关系曲线Fig.13 Parameter 1/as versus deviator stress amplitude［freezing negative temperature（a），coarse particle content（b），stress path（c）］

根据马-准则，绘制回弹模量与循环动荷载次数关系曲线，用回弹模量曲线稳态拐点来表征后循环压实阶段与二次循环变形阶段的边界点，记为Nc，并计算Nc与10Nc循环次数之间的平均塑性应变率。图14 为平均应变率εdif与偏应力幅值关系曲线。可以看出与上述两种准则相比评估结果有所不同，在图14（a）中，-2 ℃冻结试样在qampl=150、200、300 kPa动应力下的试验结果均归于塑性蠕变；在图14（b）中，粗颗粒含量对平均塑性应变率的影响与偏应力幅值呈正相关关系，即在300 kPa 的动应力下粗颗粒含量效应更显著；在图14（c）中，在k=-3.0 和k=-1.5 的应力加载路径中回弹模量曲线过于离散，无法找到准确的稳态拐点，故难以得到可靠的安定性评估结果。

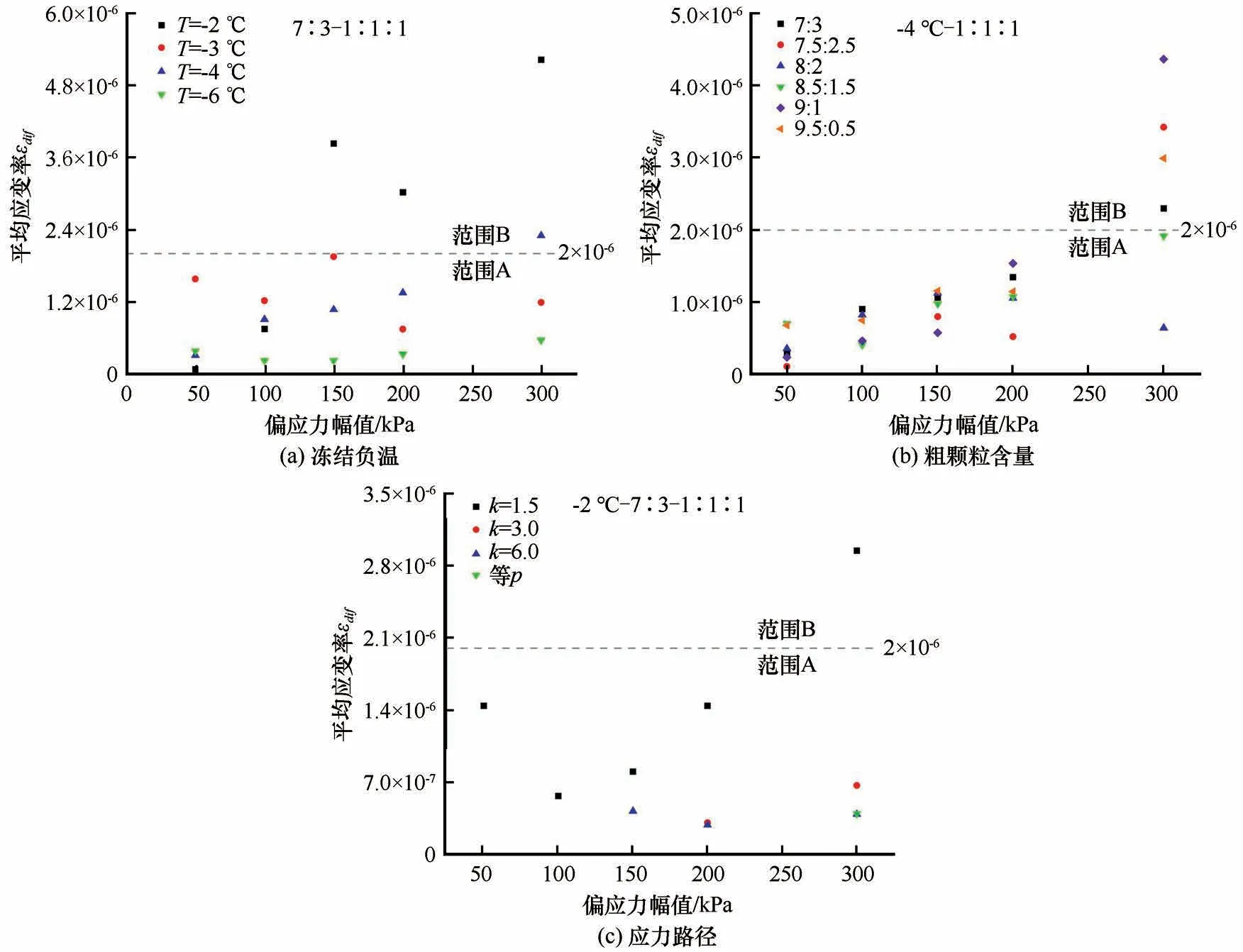
图14 Nc～10Nc间平均应变率εdif与偏应力幅值关系曲线Fig.14 Average strain rate εdif between cyclic number Nc and 10Nc versus deviator stress amplitude［freezing negative temperature（a），coarse particle content（b），stress path（c）］

将所有冻结试样中含区域B的试验结果按照上述三类安定性评估准则的评判标准进行分类汇总，如表5 所示；而未列于表5 中各试样的安定性评估结果均属于区域A，即塑性安定区，占本文试验条件下的冻结路基填料试样的大多数。从表5中评估结果对比发现，在恒围压加载的试验条件下Werkmeister-准则仅有2个试验结果超过塑性安定范围，进入塑性蠕变区，而通过马-准则评判为塑性蠕变的结果共有10个，说明马-准则在恒围压条件下（单向循环应力条件下）容易进入塑性蠕变阶段（B 区域），这是由于马-准则主要考虑了临界循环应力次数以后累积塑性应变率，其更能考虑接近真实交通长期荷载条件下的路基累积塑性变形；在动围压加载的试验条件下对于达到塑性蠕变范围的11 个结果，Werkmeister-准则和马-准则得到完全相反的评定，前者占区域B的结果共9个，后者仅含2个，这与恒围压加载条件下两评估准则的评判情况正相反，说明Werkmeister-准则在动围压条件下（双向循环应力条件下）更容易进入塑性蠕变阶段（B区域），轴向塑性应变在前5 000 次的积累较为迅速，所以Werkmeister-准则以前3 000 至5 000 次循环的塑性变形差值来判定路基的累积变形具有一定的局限性；此外，陈-准则评估恒围压和动围压加载条件下所有冻结试样的试验结果均为塑性安定。

4 结论

本文针对寒区铁路冻结路基填料，开展多级循环动三轴试验以此模拟在长期交通荷载条件下冻结路基填料的动力学过程，试验确定了不同冻结负温、粗粒级配及应力路径下的累积变形和回弹变形特征，验证Werkmeister-准则、陈-准则及马-准则对于冻结路基填料的适用性，得出以下主要结论：

（1）冻结路基填料的轴向累积塑性应变随循环加载作用次数的增大而增大，同一偏应力幅值下的应变曲线均可分为后循环压实阶段与二次循环变形阶段；恒围压试验中体变随循环加载作用次数的增大而增大，而动围压试验中模拟原位交通荷载下双向循环的应力状态，在不同应力路径中产生剪胀和剪缩的交替变化；轴向累积塑性应变率与塑性应变成负相关关系；回弹模量随循环加载作用次数的变化趋势与先期固结压力有关，欠固结状态下曲线增长至稳定，超固结状态下曲线减小至稳定。

（2）在CCP 试验中轴向累积塑性应变随冻结温度的升高而增大且随偏应力幅值的增加而更明显，随粗颗粒含量的增大而减小；体变随冻结温度的升高先减小再增大，随粗颗粒含量的增大则是先减小再增大后减小；回弹模量与冻结温度和粗颗粒含量无显著的演化趋势。

（3）在VCP 试验中轴向累积塑性应变随应力加载路径的改变呈先增大再减小后增大的变化趋势且与偏应力幅值呈正相关关系；随偏应力幅值的增加，体变在k=1.5、3.0、6.0 的应力路径上呈上升趋势，在等p的应力路径上平稳发展，在k=-3.0、-1.5的应力路径上呈下降趋势。

（4）基于三类安定性准则评估和判定了多级循环加载下冻结路基填料的累积塑性变形结果：Werkmeister-准则和马-准则分别在动围压（双向循环）条件下和恒围压（单向循环应力）条件下更易进入塑性蠕变阶段，而陈-准则在任一条件下的评判结果均属于塑性安定范围，此外后循环压实阶段与二次循环变形阶段临界点的确定方法不同对安定性评估结果的影响有不可忽视的作用。