球模仪测试冻结砂长期抗剪强度的双球模型解答及其试验研究

恽晴飞， 谢春磊， 张 泽， 刘有乾， 付峻松， 刘 启

（1.上海长凯岩土工程有限公司，上海200093； 2.东北林业大学土木工程学院/交通学院/寒区科学与工程研究院，黑龙江哈尔滨150040；3.兰州大学土木工程与力学学院，甘肃兰州730000； 4.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州730000； 5.内蒙古自治区交通建设工程质量监测鉴定站，内蒙古呼和浩特010051；6.中国铁路青藏集团有限公司，青海西宁810000）

0 引言

我国冻土分布十分广阔，其中仅多年冻土区的面积就占国土总面积的22.4%［1］。冻土作为一种特殊性土，受到土中冰胶结物的影响，具有许多融土所不具有的性质［2-3］。而在冻土的诸多性质中，冻土的变形与强度问题是影响冻土区工程建设的基本问题［4-5］。目前，已有许多学者针对冻土的变形与强度进行了研究，但这些研究大多基于三轴试验或直剪试验得出结论，针对球形模板压入仪试验（以下简称球模仪试验）的理论研究仍相对较少。以往的学者在借助球模仪试验研究冻土的物理力学性质时，主要针对冻土的长期强度进行研究，张泽等［6］对冻结冰渍亚黏土的长期强度随冻融循环次数变化的规律进行了研究；周泓等［7］以重塑黄土为研究对象，分析不同冻融循环次数作用下土体黏聚力长期强度的变化规律；陈鑫等［8］以饱和冻结砂土、粉土、黏土为研究对象，通过球模仪试验对其长期强度进行测试，并对其长期强度进行了预报。可见球模仪试验在研究冻土长期强度这一方面已应用比较成熟，试验结果可信度也较高。但受限于球模仪试验过程中试样所受应力与随之产生的应变较难界定，适用于该试验的应力-应变模型难以建立［6］。一般而言，球模仪试验通过球形模板压头（以下简称球形压头）压入土体的深度来估算土体的强度与力学指标，因此建立试样受力情况和被压头压入深度之间的联系是可行的。

因此本文基于球模仪试验，以不同粒径组制成的饱水冻结砂土（饱水状态下试样含水率受颗粒尺寸影响）为研究对象，研究冻土试样在其他试验条件不变，仅上部固定荷载不同的条件下被球形压头压入土体深度随时间的变化规律。通过对各粒径组冻结砂土之间相互对比参照，总结得到不同固定荷载试验条件下球形模板压头压入冻结砂土试样深度St之间的相互转换关系，进而探究冻土的长期抗剪强度变化规律。

1 试验方法及理论介绍

1.1 球模仪试验介绍

球模仪试验已比较广泛地应用于俄罗斯的冻土力学研究中，逐渐成为测试冻土力学性质的一种常见试验方法［6］。相较于常规的三轴试验与直剪试验，球模仪试验具有试验周期短，制样要求较低，并可进行野外和室内试验的优点，缺点为对试验土样的均一性要求较高［9］。球模仪试验原理的建立基于理想黏性非强化体的塑性理论，与布氏（Brinnel）硬度仪的实验原理相似，球模仪试验的简图如下图所示。

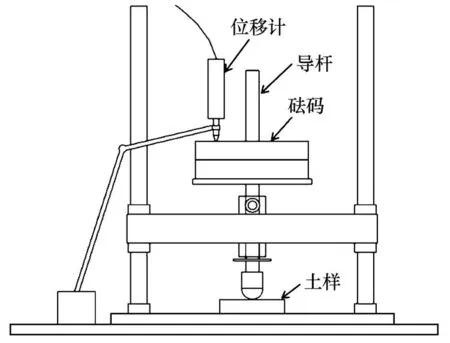
图1 球模仪简图Fig.1 Diagram of spherical template indenter

采用球模仪进行试验时，将球形压头放置于冻土试样的表面，然后借助导杆施加恒定荷载P，测量从开始加载至加载超过24 h 后的球形压头压入土体的深度St（如图2 所示），便可计算出冻土的平均阻力，也就是黏聚力C值。根据崔托维奇［6］的建议，考虑冻土中内摩擦力的影响，将黏聚力C视为等效黏聚力Cэ，记为Cэ=Ct。Ct是塑形土黏聚力的综合指标，表征了冻土试样在外荷载作用下表现出的所有强度指标。

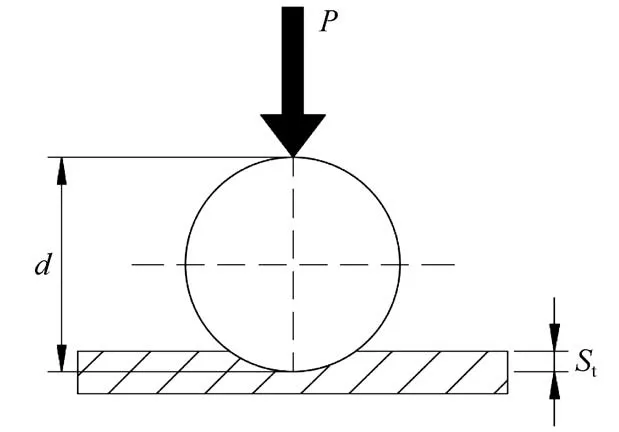
图2 球形压模仪试验示意图Fig.2 Schematic diagram of the spherical template indenter test

同时，在球形压头压入冻土体的过程中时，冻土试样随着球形压头压入时间发生蠕变，压头与试样之间的接触面积也随之增大，作用于试样表面的应力也会相应减小，这一动态平衡的过程促进了土体的稳定，这一过程就是冻土试样长期强度随时间降低的过程。

式（1）为球模仪试验计算冻土等效黏聚力Ct的理论公式：

式中：Ct为单位面积随时间变化的等效黏聚力（MPa）；P为作用在球形压模仪的竖向荷载（kg）；K为比例系数，一般取值为0.18；d为球形压球直径（mm），建议选用22 mm 球形压头进行试验；St为随时间球形压头压入土体的深度（mm）［6］。

如果加载后（在5～10 s内）立即测定球的压入深度St，那么所求出的等效黏聚力实际上可作为瞬时黏聚力；而如果St相当于球稳定状态（长期极限）压入深度，那么在St=S∞时，式（1）计算的等效黏聚力则为长期极限黏聚力［9］。

通过式（1），已知球的直径d及荷载P，并测得在荷载P条件下随时间的压头压入深度St（图2），便可以求出相应于各时刻的冻土等效黏聚力Ct。

同时，为确保试验全过程土样不受外部条件影响，试验全程均在环境箱中进行，环境箱实拍图如图3所示，相关技术指标见表1。

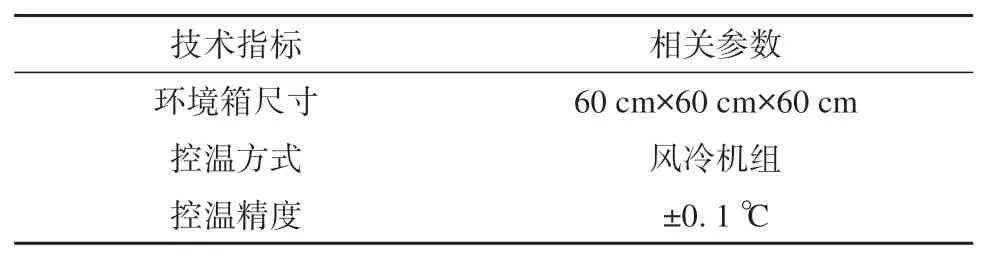
表1 环境箱技术指标表Table 1 Environmental box technical specifications table

图3 环境箱实拍图Fig.3 Environmental box real shot

1.2 试验材料及制样介绍

一般而言，影响土体强度的指标主要有两个：黏聚力c和摩擦角φ。而正温状态的砂土黏聚力c可忽略不计，当受压土体变形较小时，球模仪试验所测出的等效黏聚力仅为砂土与冰胶结后新产生的黏聚力［10］，冻结砂土的抗剪强度均由等效黏聚力提供（下文分析时均描述为冻结砂土的抗剪强度）。这对确定影响冻结土强度的因素是有利的，因此本文以砂土为研究对象。在试样制备过程中，不同粒径的石英砂制样难度与效果不同，对试验结果也有不同程度的影响［9］。为使试验结果更加可靠，本文选用标准石英砂进行试验，并选取三组不同粒径范围的砂粒组进行对比，三组砂粒组的粒径范围分别为0.6～0.5 mm、0.5～0.4 mm、0.4～0.315 mm。

在确定以标准石英砂为研究对象后，通过筛分法对其进行粒级分组，如表2 所示。在标准环刀（61.8 mm×20 mm）中进行制样，制样时首先用保鲜膜封死环刀的底部，并将封死底部的环刀放置于大小适中的硬塑料盒中，这确保了砂土在冻结过程中外表面能够保持光滑且受外部扰动较小；其后将筛分过的标准石英砂均匀平铺于环刀之内，且每铺一层均用小锤多次敲击环刀的外壁，确保砂土颗粒之间紧密接触；接着将试样放置于真空饱和箱之中进行24 h 的抽真空及进水饱和；最后将饱和完成的试样用保鲜膜封死。防止冻结过程中试样水分损失，将其放入设置好温度的恒温冰箱之中冻结24 h。

表2 冻结砂土试验分组表Table 2 Frozen sand test grouping table

球模仪试验中，冻土体的强度指标是试样在不同外荷载作用下的具体表征，因此两者之间具有一定的相互关系。不同固定外荷载的选用会直接影响试验结果，尤其是对试验过程中球形压头压入土体速度的影响最为显著，这就要求外荷载的选用需满足一定的要求。

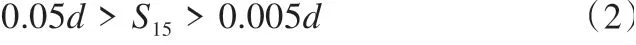
式中：S15为试验进行15 min后球形压头压入土体的深度；d为球模仪直径［6］。

一般而言，若选择的固定外荷载能使压头压入土体的深度满足上式（2），试验结果可认定为可信的。根据经验，本文外固定荷载选用5.1 kg、7.0 kg。

荷载作用下冻土强度与时间的关系总体特征都是相同的，随着时间所有强度指标都在荷载作用下降低［11-12］。另一方面，冻土的负温值也在本质上决定着冻土流变的剧烈程度（流变的速率、强度降低的速度、应力松弛）［3］。为有利于试验的进行，选取适宜的试验温度尤为重要。通过在环境箱进行预试验，不断调整试验温度，最终确定试验温度为-6 ℃，使该温度下的冻土试样能在前文所述的外固定荷载下满足式（2），具体试验参数设置如表3 所示。详细试验流程如图4所示。

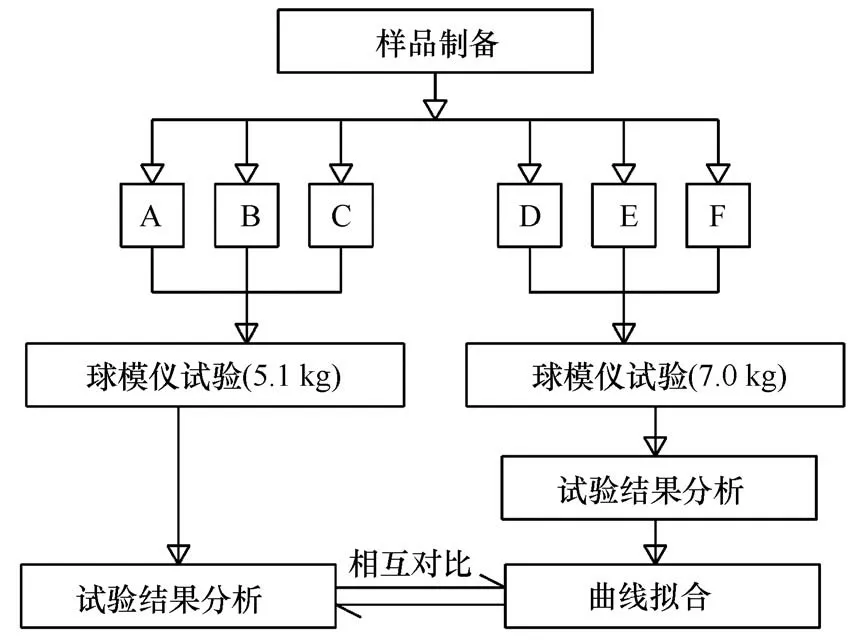
图4 试验方案设计图Fig.4 The test procedures

表3 试验参数设置表Table 3 Test parameter setting table

1.3 球模仪试验理论分析

根据弹性力学解答，两个弹性球相互接触的模型如下图5所示，图中两球在没有压力作用时，接触点仅有O点。当在上球作用一固定压力P时，两球接触面将产生一定的接触压力，并发生相对位移。根据弹性力学中的推导，两球之间的接触压力，以及接触压力所引起的位移，可用式（3）及式（4）表示，式中：P为作用在球体上的竖向荷载（kg）；St为两弹性球体在固定力P作用下的相对位移量（mm）；q0为两弹性球体在固定力P作用下的最大接触压力；k1及k2分别为上下两弹性球体的弹性常数；R1及R2分别为上下两弹性球体的半径［13］。

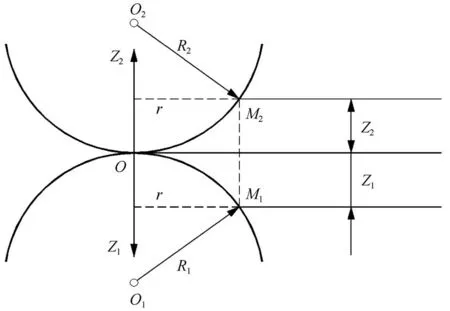
图5 弹性力学理论模型Fig.5 Theoretical model of elasticity

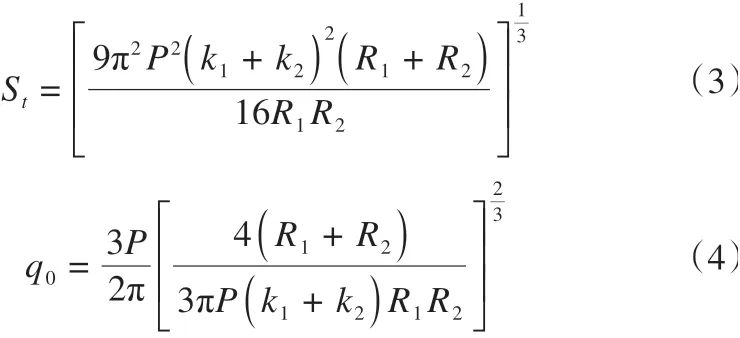
对于球模仪试验，压头可视为刚度较大的弹性球体［14-15］，试样可视为一个平面接触（R1= ∞）。因此，令R1→∞便可得到球体放置在平面上时，上部弹性球体在固定力P作用下产生的位移量及弹性球体与平面之间的接触压力，如式（5）及式（6）。

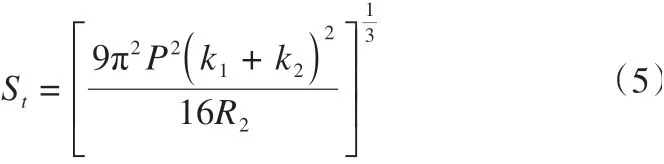
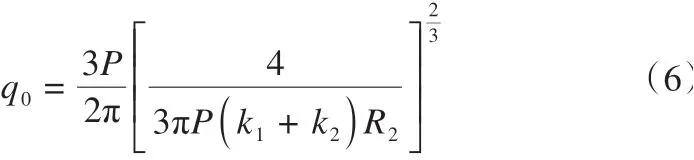
可见对于弹性球体压入平面的过程中，压入深度St与接触压力q0仅与固定力P、弹性常数k1及k2、压头半径R2相关，当这些参数确定后，压入深度St与接触压力q0也随之确定。为消除弹性物体本身性质对压入深度St与接触压力q0的影响，联立式（5）及式（6）以消去k1+k2，则压入深度St与接触压力q0可由固定力P、压头半径R2这两个参数表征，如式（7）。

由式（7）可知：压入深度St与接触压力q0之积与固定力P成正比，与压头半径R2成反比。当固定力P与压头半径R2一定时，压入深度St与接触压力q0呈共轭关系，即在固定力作用下，保持压头半径一定，随着压入深度的增大，最大接触压力q0会随之减小。

前文已述，崔托维奇和维亚洛夫基于球形模板压入仪试验建立了以球形压板上部竖向荷载P、球形压板直径d、球形压板压入深度St表征冻土等效黏聚力的经验公式，如式（1）。

根据式（7），压头随时间的压入深度St表征着冻土不同时刻的等效黏聚力值，q0则表示压头与冻土接触面的最大压力值，可见在球模仪试验过程中，接触面最大压力值与压头随时间压入深度之间存在一种相互对应的关系，因此可将式（7）按照式（1）的形式变形得到式（8）：

通过式（8），不难得出以下结论，当球形模板直径一定时，γ也同样为定值，本文在球模仪试验中压头直径选用为22 mm，此时转换系数γ=3.82×10-3。若能测定接触面最大接触压力q0，便能确定该时刻下的长期等效黏聚力（Ct）。通常情况下，长期等效黏聚力（Ct）需要施加固定力一定时间，通过球形模板随时间沉入试验土样的深度方可确定。建立两者之间的关系后，便可通过中间值q0将两种不同试验条件下的试验结果相互转换，从而快速得到结果。下文将针对这一点进行验证。

2 试验结果分析

2.1 球模仪试验结果分析

图6为不同颗粒尺寸冻结砂土在5.1 kg与7.0 kg荷载下长期抗剪强度随时间变化的曲线图。横坐标与纵坐标分别为冻结砂土的抗剪强度值（MPa）与球形压头压入土体的时间（s）。

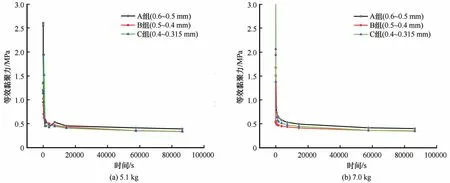
图6 冻结砂土随时间抗剪强度变化曲线Fig.6 Variation curve of shear strength of frozen sand with time：5.1 kg（a）；7.0 kg（b）

在球模仪试验的全过程中，冻结砂土在5.1 kg与7.0 kg 荷载下长期抗剪强度随时间的变化曲线呈现出了相同的规律，即冻土蠕变的速率在球形压头刚压入的10 min 内蠕变速度较快（稳定蠕变阶段），此时冻土的变形主要表现为黏弹性变形；球形压头压入30 min～1 h 后，冻结砂土的蠕变速率有所降低，但还是较快（衰减蠕变阶段）。球模仪试验进行24 h 后，冻结砂土的抗剪强度基本不发生变化，达到了稳定值，此时的抗剪强度就可认为是冻结砂土的极限抗剪强度［16］。

通过纵向对比由不同粒径组石英砂制成的冻结砂土抗剪强度随时间的变化曲线，发现在固定荷载的条件下（分别为5.1 kg、7.0 kg）冻结砂土的抗剪强度与砂土的颗粒尺寸呈正相关，即石英砂颗粒尺寸越大，所制成的冻结砂土的长期抗剪强度也就越大［17-18］，这一规律在整个球模仪试验过程中均成立，即颗粒尺寸越大，冻结砂土的瞬时抗剪强度、中间抗剪强度、极限抗剪强度均越大。

球模仪试验时所制试样均为饱水试样，但由于组成冻结土的颗粒尺寸不尽相同，试样在饱水状态下的饱和含水率也各不相同。表4为不同粒径组冻结砂土试样含水率实测值，图7 为含水率测试试验过程的实拍图。

图7 不同粒径组冻结砂土含水率测试实拍图Fig.7 Real pictures of moisture content test of frozen sand with different particle size groups

表4 不同粒径组冻结砂土试样含水率Table 2 Moisture content of frozen sand samples of different particle size groups

测试结果表明，对于需要饱水的冻土试样，由于饱水前各粒径组试样的孔隙比不同，饱水后其含水率也不同，可以认为冻结砂土的颗粒尺寸直接决定了含水率的大小。同时，由于松散砂土试样在正温时基本不具备强度，冻结后其强度主要由颗粒与冰之间的胶结力提供，因此冻结砂土试样饱水冻结后的含冰量直接决定了强度特性指标［9］。即冻结砂土含冰率与其长期抗剪强度呈正相关［1，9］。这与上文所述的冻结砂土颗粒尺寸与其长期抗剪强度呈正相关的结论在本质上相统一。

2.2 拟合结果分析

上文推导得出了作用于球模仪上荷载及球形压头直径确定的条件下，球形压头压入深度St与冻土表面最大接触压力q0之间存在共轭的关系。因此可通过最大接触压力q0这一中间参数将不同固定荷载下球形压头压入深度进行换算。基于这种方法，理论上便可将非常规试验条件下球形压头压入土体的深度转换为常规试验条件下球形压头压入土体的深度，从而快速地换算出冻土的长期抗剪强度，极大地提高球模仪试验的适用范围。

在固定荷载为5.1 kg 的球模仪试验中，球形压头压入土体深度为St1，在固定荷载为7.0 kg 的球模仪试验中，球形压头压入土体深度为St2，利用式（7），将固定荷载为7.0 kg 的球模仪试验中球形压头随时间压入土体深度转换为理论上5.1 kg 固定荷载作用下球形压头随时间压入土体深度，并与试验实际测定的5.1 kg 固定荷载作用下球形压头随时间压入土体深度进行对比，如图8所示。

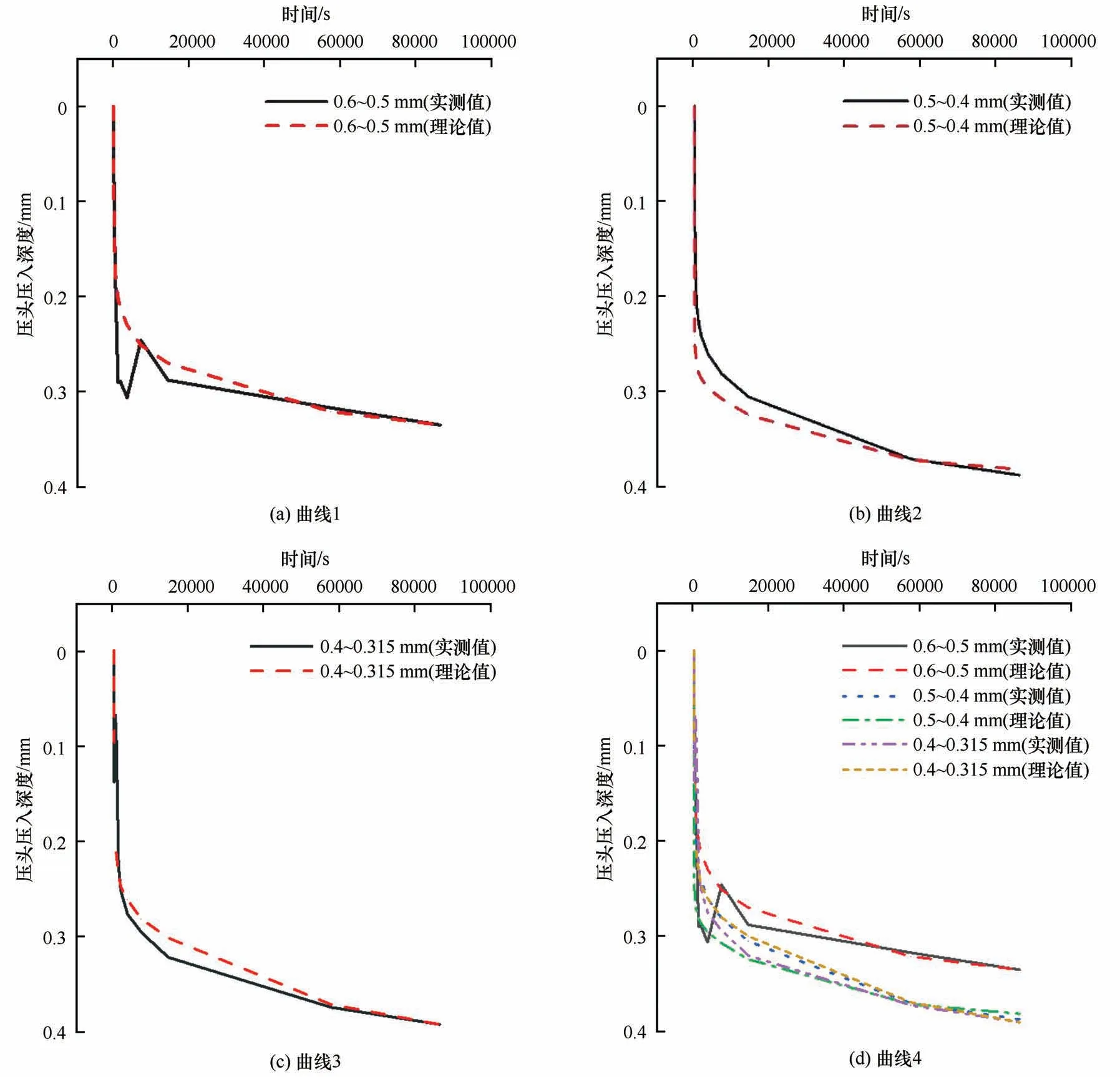
图8 冻结砂土随时间压头压入深度变化Fig.8 Variation of indentation depth of frozen sand with time：curve 1（a）；curve 2（b）；curve 3（c）；curve 4（d）

图8 为通过式（7），将固定荷载为7.0 kg 下球形压头压入土体的深度进行转换（图中理论值曲线），并与固定荷载为5.1 kg下球形压头压入土体的深度曲线进行对比（图中实测值曲线）。球模仪试验中，球形压头压入土体的深度由快转慢，在刚压入的前10 min最为迅速，对应了冻土的黏弹性变形；球形压头压入30 min～1 h 后，球形压头压入土体的速度开始放缓，对应冻土的衰减蠕变阶段；最终在试验进行约24 h，球形压头压入土体的深度基本趋于平缓。

对比理论值曲线与实测值曲线，各粒径组中这两条曲线均表现出比较一致的规律性，且理论值曲线与实测值曲线符合程度较高，基本可实现通过理论值曲线对实测值曲线进行预测。这也证明了式（7）的可行性。同时，本文也将三个粒径组的理论值曲线与实测值曲线进行横向对比，结果表明：不论是理论值曲线还是实测值曲线，相同直径球形压头压入颗粒尺寸较大的冻结砂土中时，压入土体的深度相对较小。

根据压头压入土体的深度绘制得到各粒径组冻土试样在5.0 kg、7.1 kg 荷载作用下的抗剪强度变化曲线，并与拟合得到的抗剪强度变化曲线进行对比，如图9所示。

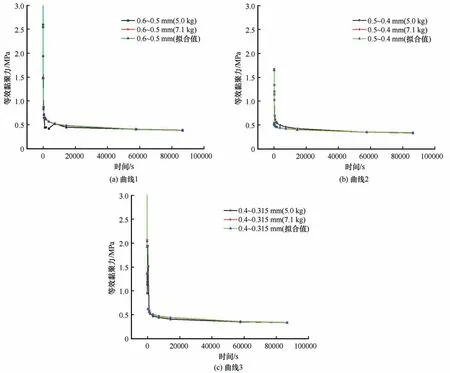
图9 冻结砂土随时间长期黏聚力变化Fig.9 Long-term cohesion change of frozen sand with time：curve 1（a）；curve 2（b）；curve 3（c）

以往的球模仪试验结果表明，不适宜的外部荷载会直接影响到试验结果的准确性，因此试验过程中外部荷载需满足一定的条件，此时外部荷载不同时得到的冻土长期抗剪强度相似的变化规律，最终土体趋于稳定时的稳定值也基本一致［19］。将基于不同外部荷载条件下得到的长期抗剪强度变化曲线与拟合得到的长期抗剪强度变化曲线进行对比，三种方式得到的长期抗剪强度变化曲线具有相同的变化趋势，且长期抗剪强度在试验进行24 h 后基本稳定，各粒径组长期抗剪强度值基本保持一致。

需要注意的是，本文通过式（7）仅验证了球模仪试验中，荷载一定时压头压入土体深度具有一定的相互转换关系，未进行变荷载条件下压头压入土体深度随时间变化的相关试验，后期可进行相应的变荷载试验，以扩大该理论的适用范围。

3 结论

基于球形模板压入试验，针对冻结砂土的长期抗剪强度进行研究，得到结论如下：

（1）基于球模仪试验得到的冻结砂土长期抗剪强度与其颗粒尺寸成正相关，同时由于冻土试样含冰率与其颗粒尺寸成正比，因此冻结砂土长期抗剪强度也随试样含冰率同比增大。

（2）冻结砂土长期抗剪强度与试验过程中冻土与压头接触面上的最大接触压力存在一定的联系，可表述为Ct=γq0。其中关系系数γ 的大小与球形压头的直径呈反比，本研究球模仪试验中球形压头选用为22 mm，γ=3.82×10-3。

（3）通过建立最大接触压力q0与长期抗剪强度Ct之间的联系，不同固定荷载下最大接触压力q0相同时，其长期抗剪强度Ct也相同，据此可换算不同固定荷载下冻结砂土随时间被球形压头压入土体的深度曲线和冻结砂土随时间长期抗剪强度变化曲线。经过试验验证，7.0kg 固定荷载下压头压入土体深度随时间变化的换算曲线与5.1 kg、7.0 kg固定荷载下压头压入土体深度随时间变化的试验实测曲线具有较高的一致性。