主应力轴旋转条件下冻结黏土的动强度特性

2022-06-14张斌龙王大雁雷乐乐周志伟

冰川冻土 2022年2期

张斌龙，王大雁，马巍，雷乐乐，周志伟

（1.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州730000； 2.中国科学院大学，北京100049；3.东华理工大学土木与建筑工程学院，江西南昌330013）

0 引言

冻土作为一种由矿物颗粒、冰、未冻水和气体组成的特殊土，在中国分布广泛，其中多年冻土区约占陆地国土面积的22.4%。随着经济的快速发展，人们对寒区空间利用和资源开发的需求日益增加，修建在寒冷地区冻土基础上的工程越来越多，如青藏铁路、拉洛水库、哈大高铁、漠河古莲机场等。而在工程建设和运行期间，冻土基础都不同程度受到动荷载的扰动，由动荷载扰动引起的构筑物失稳和破坏也时有发生。因此，研究冻土动强度对寒区冻土地基、路基和边坡等工程设计和稳定性评价具有重要的理论和实际意义。

目前，许多学者已经关注到冻土动强度对寒区工程和人工冻结工程设计的重要性，开展了大量试验研究，并取得丰硕的成果。Zhao 等［1］研究了循环荷载作用下围压和含盐量对冻土动强度的影响，发现含盐冻结粉土的剪切强度随围压的增大先增大后减小，而随着含盐量的增加先减小后增大，并根据试验结果建立了考虑含盐量影响的含盐冻结粉土动强度准则；赵福堂等［2］通过分级循环加载试验研究了冻结温度、围压和频率对冻结盐渍土动强度特性的影响，发现围压升高和温度降低都能显著提升冻结盐渍土的动强度，而频率的变化对其动强度特性影响较小；栗晓林等［3］研究了振动荷载作用下温度和频率对冻结砂土动强度特性的影响，发现温度降低对冻结砂土动强度影响显著，频率变化对动强度影响较小，而温度与动强度呈线性关系；张淑娟等［4］探讨了不同围压下动强度相对耗散能的变化，证实随着耗散能的增大冻结粉质黏土的动强度逐渐减小。另外，许多学者还通过SHPB 试验对冻土冲击动强度特性进行了研究［5-8］。以上研究主要聚焦于冻土在主应力方向固定条件下动强度规律的演化，少有研究关注到主应力轴循环旋转条件下冻土的动强度特性。事实上，在波浪、交通、地震等动荷载作用下，地基、路基和边坡等受力条件比较复杂，动荷载作用时不仅发生应力幅值的循环变化，还伴随着主应力轴循环旋转现象。虞海珍［9］、聂影［10］分别研究了复杂应力路径下钙质砂和重塑黏土的动力特性，发现主应力轴旋转将加速累积塑性应变和孔隙水压发展，从而降低动强度；赵宇［11］进行了不同荷载方式（循环圆扭剪、循环椭圆扭剪、循环扭剪、循环三轴）的不排水粉土动力试验，发现不同应力路径下粉土动强度存在较大差异，循环圆扭剪应力路径下动强度最小；沈扬等［12］研究了主应力轴旋转时软黏土的动强度特性，发现考虑主应力轴旋转时的动强度相比循环三轴试验结果明显减小；李男等［13］研究了椭圆应力路径下饱和松砂动强度特性，发现考虑主应力轴旋转的椭圆应力路径下动强度小于循环三轴动强度；周健等［14］研究表明当含水率达到一定程度时，考虑主应力轴旋转的圆形应力路径下铁精矿的动强度小于循环三轴动强度；杨爱武等［15］研究了主应力轴旋转条件下振幅和波形对天津滨海吹填土动力特性的影响，发现波形对累积应变影响具有临界效应，而考虑主应力轴旋转时正弦波加载的动强度最小。可见，考虑主应力轴旋转时融土的动强度明显减小，而不考虑主应力轴旋转的影响将高估实际工程中土体的动强度，给工程稳定性带来不利影响。然而，受制于试验仪器，目前还未有文献报道主应力轴旋转条件下冻土的动强度特性，主应力轴旋转对冻土动强度特性的影响也尚不清楚。

鉴于此，本文以冻结黏土为研究对象，利用冻土空心扭剪仪（FHCA-300）开展循环三轴加载试验和圆形循环耦合剪切试验，对比研究了不同围压下主应力轴循环旋转对冻土动强度特性的影响，以期为寒区工程和人工冻结工程设计提供有益参考。

1 材料与方法

1.1 试样制备

试验所用土料取自青藏铁路沿线北麓河段，根据《土工试验方法标准》［16］分别进行了液塑限联合试验、击实试验、抽真空饱和试验、比重瓶试验和颗粒筛分试验，对试验用土的基本物理性质进行测试。测试结果显示，试验用土的液限为34.5%，塑限为13.9%，塑性指数为20.6，最大干密度为1.72 g·cm-3，最优含水率为18.2%，饱和含水率为19.6%，土粒相对密度为2.71。根据土的工程分类标准，试验用土归属于低液限黏土，其颗粒的级配曲线如图1所示。

试验采用高200 mm、外径100 mm 和内径60 mm的重塑空心圆柱试样。重塑空心圆柱试样制备流程如下：将取回的试验用土风干、碾碎，过2 mm圆孔筛，根据目标含水率将定量的蒸馏水加入准备好的干土中并用手搅拌均匀，将其过2 mm 方孔筛，随后装入密封袋保存24 小时使水分分布均匀。制样时根据试验试样的密度称取一定质量的闷料，分五层装入自制的空心圆柱制样模具，然后使用压样机正反压密至目标高度，最后脱模即可得常温空心圆柱试样，具体空心圆柱试样制备流程如图2所示。将常温空心圆柱试样快速装入冻土空心圆柱仪的压力室，在-30 ℃下快速冻结12 h，防止试样中水分迁移和冻胀发生，然后调节温度至-5 ℃保持24 h使试样温度分布均匀，即可得到试验的冻土空心圆柱试样。

图2 空心圆柱试样的制备流程Fig. 2 Process for preparing hollow cylindrical specimens

1.2 试验方案

试验在冻土工程国家重点实验室的冻土空心扭剪仪上进行，仪器能够在负温环境下施加轴向应力、扭矩、内围压和外围压四个方向应力，从而可以实现定向剪切和主应力轴旋转等多种应力路径。进行动力加载试验前，在-5 ℃温度下以1%·min-1的轴向应变率进行单轴试验和围压为400 kPa、700 kPa 和1 000 kPa的常规三轴压缩试验。试验表明，-5 ℃下围压为400 kPa、700 kPa 和1 000 kPa 时冻结黏土的强度在4 000～4 500 kPa，试样破坏应变在15%左右。参考三轴静力试验强度结果，当施加围压分别为400 kPa、700 kPa 和1 000 kPa 时，动荷载试验的剪应力幅值设定为2 000、2 250、2 500、2 750 和3 000 kPa，具体的试验方案见表1。循环剪应力幅值对冻结黏土动力特性的影响通过循环应力比（cyclic stress ratio，CSR）来表征［17］，计算公式如下。

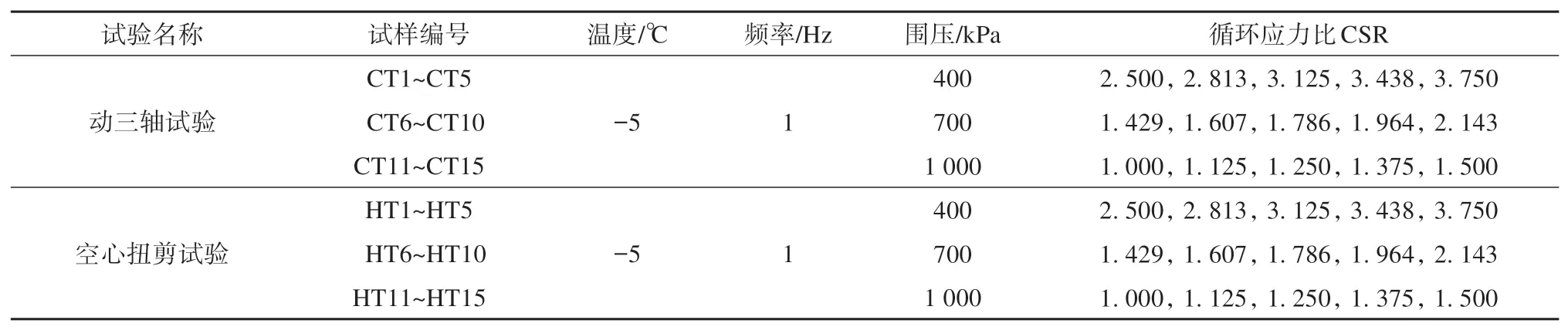
表1 试验方案Table 1 Scheme of the tests

式中：qcyc为循环剪应力幅值，数值上等于主应力轴连续旋转圆形应力路径的半径或循环三轴加载的动应力幅值；p0为初始围压。

根据上述试验方案，分别开展不同围压下冻结黏土动三轴和空心扭剪试验。在进行动三轴和空心扭剪试验前，对试样施加围压和对应的静偏应力，保持一定的时间使试样受力稳定。然后，对试样以1 Hz 震动频率施加动荷载，动三轴试验施加的轴向应力波形和实现的应力路径如图3 所示，空心扭剪试验施加的轴向应力、扭矩波形和实现的应力路径如图4所示。动荷载试验的终止采用双重条件控制，若震动次数达到10 000 次时，冻结黏土试样轴向应变仍未达到15%，冻结黏土试样未发生破坏，震动次数10 000 次即为试验的终止条件；若震动次数小于10 000 次时，冻结黏土试样轴向应变已经达到15%，认为冻结黏土试样提前破坏，轴向应变15%即为试验的终止条件。

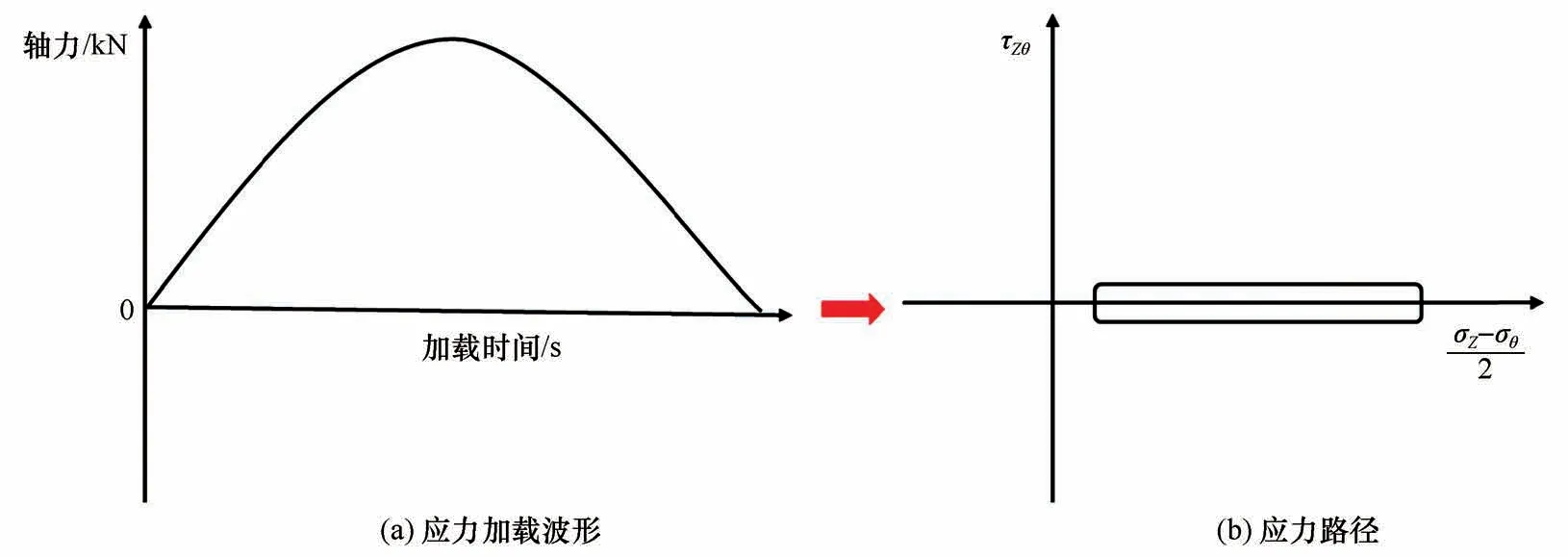
图3 动三轴试验轴向应力加载波形和实现的应力路径Fig. 3 Axial stress loading waveform（a）and stress path（b）in dynamic triaxial tests

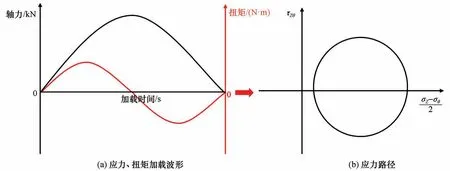
图4 空心扭剪试验轴向应力、扭矩加载波形和实现的应力路径Fig. 4 Axial stress，torque loading waveforms（a）and stress path（c）in hollow torsional shear tests

2 结果与分析

2.1 静三轴试验

为了选取合适的动应力幅值，首先进行了静三轴试验，以确定冻结黏土试样的静强度。图5 给出了不同围压下冻结黏土试样的偏应力-轴向应变曲线。可以看出，随着轴向应变的增大，偏应力先增大后不同程度减小，所有冻结黏土试样出现应变软化现象；围压越大时，冻结黏土试样软化现象越弱。此外，围压越大时，冻结黏土试样的偏应力峰值越大，偏应力变化范围为4 000～4 500 kPa之间。

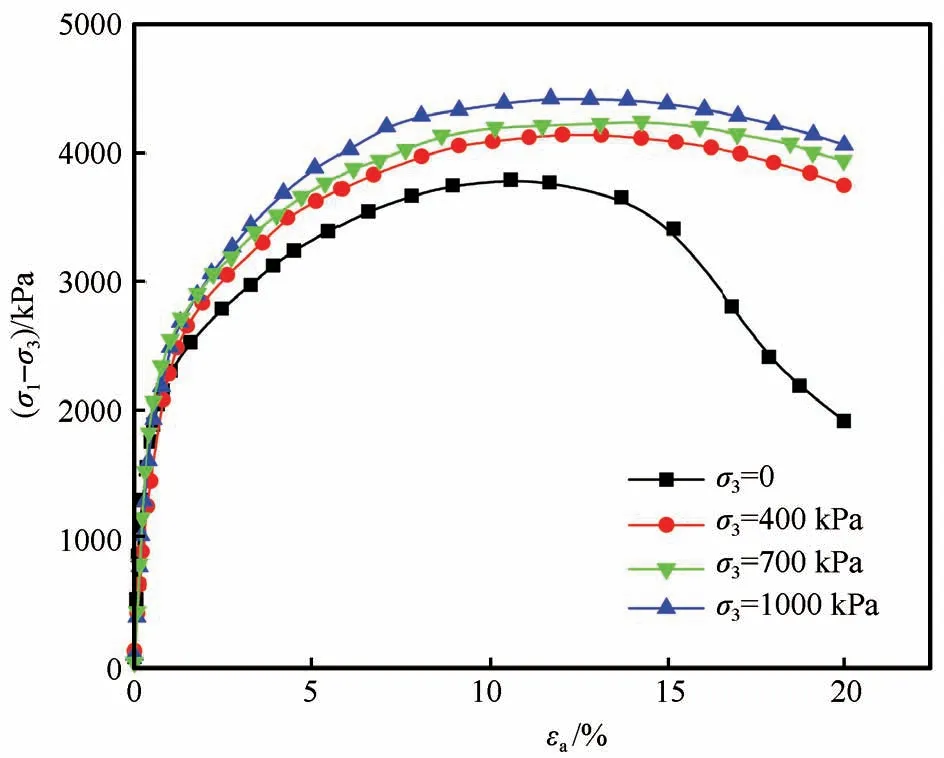
图5 不同围压下冻结黏土试样的偏应力-轴向应变曲线Fig. 5 Deviatoric stress-axial strain curves of frozen clay specimens under different confining pressures

2.2 动强度变化

土的动强度是指动荷载震动一定的次数后达到某一规定的破坏标准时所对应的动应力幅值。对于破坏标准的选取有多种方法，但在冻土动强度研究中，一般采用应变破坏标准。根据地基土的情况和工程重要性，常用的应变破坏标准有3%、5%、10%和15%。本文保守考虑冻土地基的稳定性，因此选取较小轴向应变3%作用破坏标准。绘制冻土试样达到破坏应变标准时震动次数与对应动应力幅值之间的关系曲线，即冻土的动强度曲线。图6给出了不同围压下冻结黏土动强度的变化曲线。可以看出，冻结黏土动三轴试验和空心扭剪试验的动强度曲线都随着围压的增加而向上平移，表明围压的增大可以明显提升冻土动强度，从而增强冻土抵抗动应力破坏的能力。当施加的围压相同时，动三轴试验的动强度明显大于空心扭剪试验的动强度。而试验中，动三轴试验和空心扭剪试验剪应力幅值变化保持相同，动三轴试验主应力方向固定，空心扭剪试验主应力方向不断变化。这表明空心扭剪试验中冻结黏土动强度的显著降低与主应力轴旋转密切相关。以破坏震动次数100 为例，当围压分别为400 kPa、700 kPa 和1 000 kPa 时，考虑主应力轴旋转条件下动强度分别降低了大约15%、8%和4%。可见，主应力轴旋转将导致冻结黏土动强度衰减，且主应力轴旋转对冻结黏土动强度的影响在低围压下更显著，若实际工程建设中忽略主应力轴旋转的影响，将严重高估地基土体的强度。

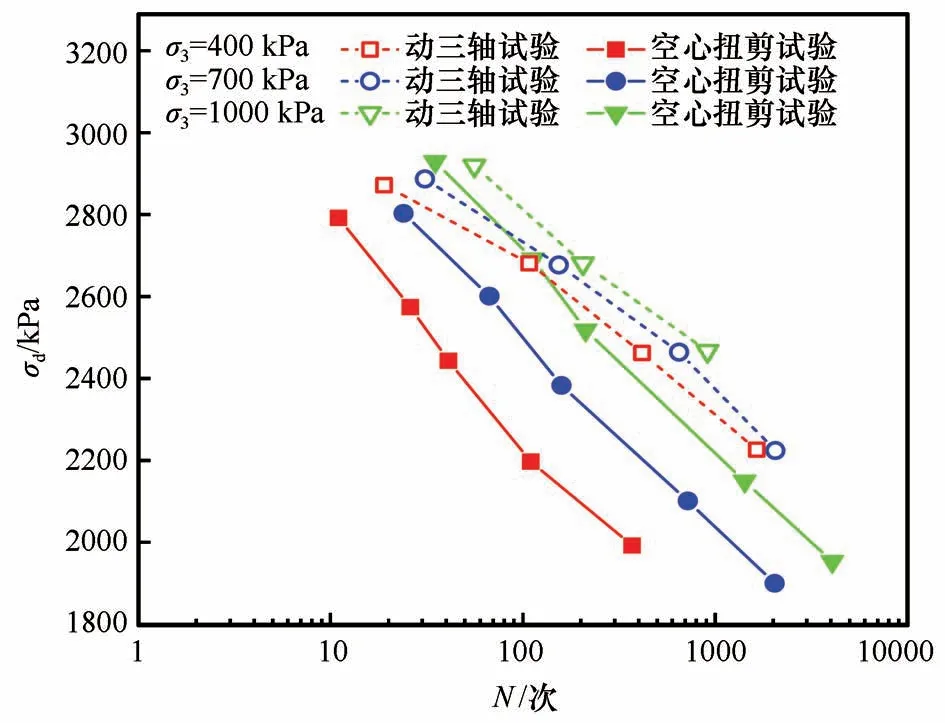
图6 不同围压下冻结黏土的动三轴试验和空心扭剪试验的动强度曲线Fig. 6 Dynamic strength curves of dynamic triaxial tests and hollow torsional shear tests of frozen clay under different confining pressures

另外，由图6 还可以看出，当其他条件一定时，冻结黏土动强度随着震动次数增多而减小，并且动强度与破坏震动次数的对数lgN近似呈线性关系。拟合公式为

式中：σd为动强度；N为震动次数；α和β为拟合系数。

利用线性方程对不同围压下冻结黏土动强度变化曲线进行拟合，拟合结果如图7 和表2 所示。可以看出，拟合曲线和实测点几乎重合，且确定系数均大于0.984，表明式（2）可以准确描述动三轴和空心扭剪试验的动强度变化规律。从拟合结果还可以看出，冻结黏土的初始动强度与围压紧密相关，围压越大，冻结黏土的初始动强度越大；当围压相同时，主应力轴旋转条件下冻结黏土动强度衰减速度明显更快。

图7 不同围压下冻结黏土动强度与震动次数关系的拟合结果与实测结果对比Fig. 7 Comparison between fitting results and measured results of the relationship between dynamic strength of frozen clay and number of vibrations under different confining pressures：dynamic triaxial tests（a）and hollow torsional shear tests（b）

2.3 动强度指标

动强度指标包括动黏聚力和内摩擦角。在计算动强度指标时，首先选定震动次数，然后计算不同围压所对应的动应力，将围压和轴向总应力绘制到σ-τ平面得到莫尔圆，做莫尔圆的强度包络线，强度包络线纵坐标的截距和斜率分别对应动黏聚力和动内摩擦角。基于上述方法，做震动次数N=50时不同围压下动三轴和空心扭剪试验的莫尔圆和强度包络线，如图8所示。可以看出，当围压在400～1 000 kPa 范围内变化时，随着围压的增加，冻结黏土动三轴和空心扭剪试验的抗剪强度都近似线性增大，不同围压下的强度包络线大致呈线性。因此，围压在400～1 000 kPa 范围内变化时，冻结黏土动三轴和空心扭剪试验的剪切破坏特性基本符合莫尔-库伦强度准则，利用莫尔-库伦强度准则可以计算出不同震动次数下动黏聚力和动内摩擦角，如图9 所示。由图9（a）可以看出，动三轴和空心扭剪试验的动黏聚力都随着震动次数的增多而减小，而空心扭剪试验的动黏聚力衰减速率明显更快，表明主应力轴旋转可以加速冻结黏土动黏聚力的衰减。由图9（b）可以看出，动三轴试验的动内摩擦角随着震动次数的增多而逐渐减小，而空心扭剪试验的动内摩擦力随着震动次数的增多而逐渐增大。此外，可以清楚发现动黏聚力和动内摩擦角与破坏震动次数的对数也呈明显的线性关系，同样可以使用式（2）来拟合动黏聚力和动摩擦角与震动次数对数的关系，拟合结果如图9 和表3 所示。可以看出，动黏聚力和动摩擦角的实测数据与拟合曲线吻合非常好，且确定系数均超过0.996，说明动黏聚力和动摩擦角与震动次数的对数呈良好的线性关系，可以根据震动次数变化来预测动黏聚力和动摩擦角的大小。

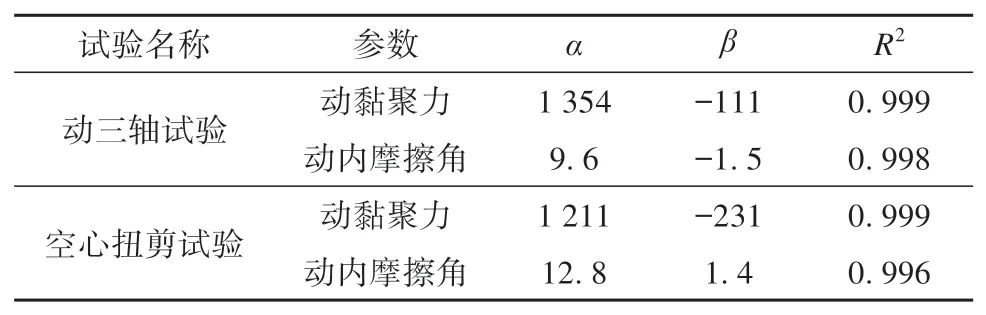
表3 冻结黏土动黏聚力、动内摩擦角与震动次数关系的拟合系数和确定系数Table 3 Fitting coefficients and determination coefficients of the relationship between dynamic cohesion，dynamic internal friction angle of frozen clay and number of vibrations

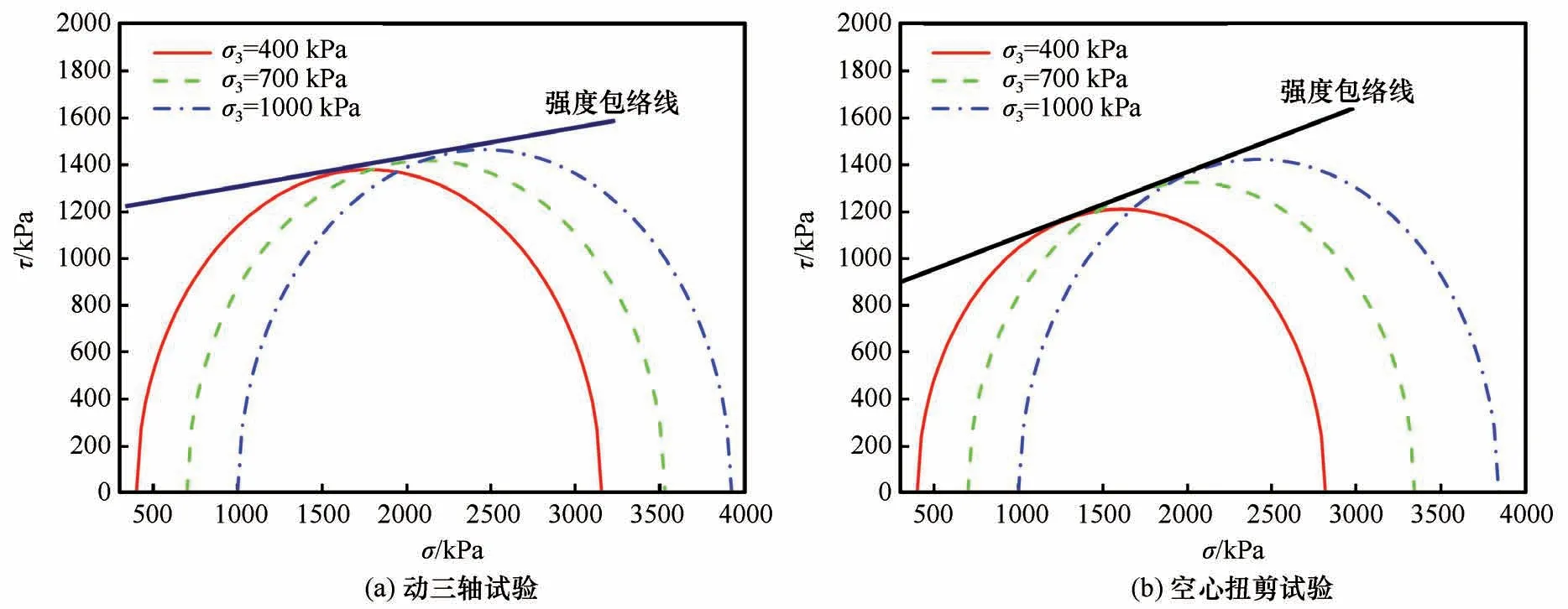
图8 不同围压下冻结黏土的莫尔圆及强度包络线Fig. 8 Mohr circles and strength envelope of frozen clay under different confining pressures：dynamic triaxial tests（a）and hollow torsional shear tests（b）

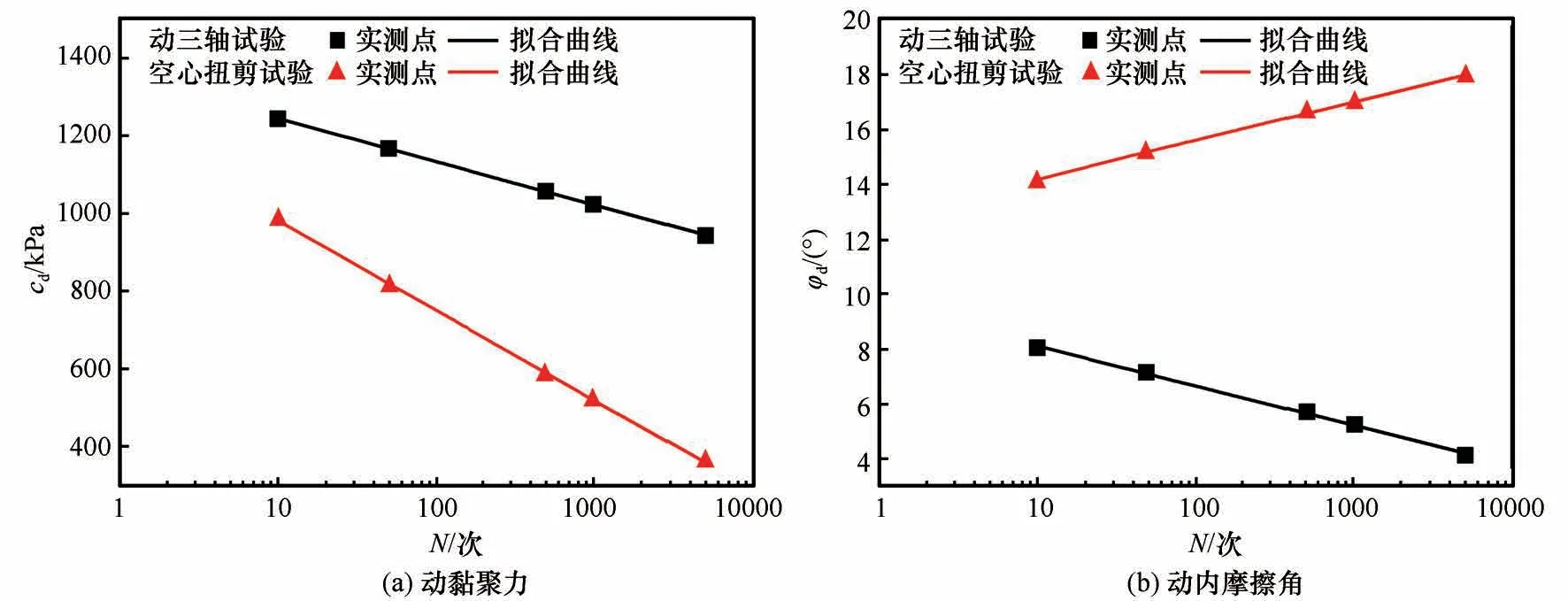
图9 冻结黏土动黏聚力和动内摩擦角随震动次数的变化曲线Fig. 9 Variation curves of dynamic cohesion（a）and dynamic internal friction angle（b）of frozen clay with number of vibrations

3 讨论

从上述试验结果看出，随着动荷载震动次数的增多，冻结黏土动三轴试验的动强度、动黏聚力和动内摩擦角都减小，而围压的增大可以提升冻结黏土的动强度，这与以往冻土动三轴试验得出的结论类似［1，4，18-19］。冻土由固体颗粒、孔隙冰、未冻水和气体组成，这也决定了冻土的强度主要由固体颗粒（黏土颗粒和冰颗粒）本身强度、冰胶结作用、固体颗粒的摩擦和咬合作用等组成。动三轴荷载持续作用下，由于固体颗粒、冰、未冻水和气体都不可压缩性，试样沿轴向发生压密时，同时发生侧向体积膨胀。在这个过程中往往伴随着颗粒的破碎和试样升温现象，冰颗粒的破碎导致固体颗粒本身强度、颗粒的咬合作用和冰的胶结能力降低，动耗散能转化为内能导致的温度升高现象不仅降低试样的抗剪强度，而且未冻水的含量将增多，使得颗粒间摩擦效果减弱［20-23］。因此，动三轴试验中冻土动强度、动黏聚力和动内摩擦角随震动次数增多而降低。而围压的增大，可以约束试样侧向变形的发生，从而增强试样固体颗粒之间的摩擦和咬合作用，增大了试样的动强度。

而不同于动三轴试验，在主应力轴旋转条件下冻结黏土动强度明显减小，并且动强度和动黏聚力随震动次数的增多而衰减速度更快，这与主应力轴旋转对融土动强度变化规律影响一致［9-15］；另外，在主应力轴旋转条件下冻结黏土动内摩擦角还随震动次数的增多而增大，这个现象鲜有文献报道。由电镜扫描和微观结构简化图可以看出（图10），黏土矿物形状一般呈片状，在沉积时应力诱导各向异性，黏土试样沿轴向的承载力大于沿水平向的承载力。由试样内部应力示意图（图11）可以看出，动三轴试验中主应力始终沿竖向分布，而主应力轴旋转时主应力与竖向存在夹角，这导致主应力轴旋转时冻土试样内部黏土矿物之间的接触部位、矿物颗粒与冰胶结部位以及冰颗粒中薄弱部位沿水平发生剪切破裂的概率相对主应力方向固定时增大，使得冰的胶结能力减弱更明显，从而冻结黏土动强度和动黏聚力降低更快；另外，相比动三轴试样，考虑主应力轴旋转时，剪切应力的耗散能同样转化为内能，导致空心圆柱试样内部温度变化相比动三轴试样可能更剧烈，温度的变化促使冰的胶结能力减弱，这也加速了土体动强度和黏聚力下降速度。由图11 还可以看出，在主应力轴旋转条件下，剪应力的存在也一定程度上促进固体颗粒沿水平向的移动，使得固体颗粒充填效果更优，冻土中固体颗粒的镶嵌、咬合加强，从而冻土中固体颗粒摩擦性能增强。因此，主应力轴旋转条件下内摩擦角随着震动次数增多而增大。主应力轴旋转条件下冻结黏土动强度参数变化表明，片理沉积结构主控的岩土体在考虑剪应力作用时，不仅发生动强度和黏聚力迅速衰减，还存在动内摩擦角增大的现象［24］。可见，冻土试样中冰胶结对强度贡献较大，而颗粒间动内摩擦作用对强度的贡献较小；当动荷载作用下冰胶结力减弱时，即使颗粒间动摩擦力增大，也无法阻止试样的动强度减小。

图10 冻结黏土电镜扫描微观结构和简化微观结构示意图［25］Fig. 10 SEM microstructure（a）and simplified microstructure schematic diagram（b）of frozen clay［25］

图11 冻结黏土试样应力示意图［26］Fig. 11 Schematic diagram of the stress of frozen clay specimen［26］：internal stress of specimen（a），rotation of principal stress axis of soil element（b），initial stress state of hollow cylindrical specimen（c）and stress state of hollow cylindrical specimen in volume expansion（d）