一种蛛网启发的农田无线传感器网络寿命优化方法

杜壮壮，王 俊，贺智涛，高 颂

（河南科技大学 农业装备工程学院，河南 洛阳 471003）

农田无线传感器网络（Farmland Wireless Sensor Networks，FWSN）是一种由大量部署于农田的传感器节点通过无线协作方式感知和处理作物生长相关信息的分布式网络系统。农田无线传感器网络节点部署密度小、分布范围广，分层分簇的路由特征致使节点能量消耗不均衡，具有由内而外分级消耗能量的特点。负担信息转发量较大的内层节点常因能量耗尽而过早死亡，造成原本连通的网络拓扑分割，导致网络的连通性与覆盖度降低，甚至引发全局网络瘫痪，网络寿命严重受限。因此，开展针对网络拓扑结构与节点能耗行为的网络寿命优化方法研究是解决FWSN规模应用瓶颈根本性问题的关键。

在拓扑结构方面，Bao N等提出了圆形不均等分层分簇优化节点部署的方法来降低网络的能耗。Zhao Z等基于一种新的网络结构模型，提出了一种在无线传感器网络中的节能集群路由协议，有效提高了网络生存周期。在节点能耗行为方面，江冰等开发了一种混合式的分簇路由算法以实现簇头节点的均匀分布与能量消耗的减少。Chen等提出了一种非均匀分簇路由协议，以达到均衡节点能耗的目的。Mostafa等通过设置全局节点初始能量异构改善全局网络节点能耗均衡表现。已开展的研究仅从节点部署方式或分簇路由算法单方面出发，均未能系统地改进FWSN的拓扑结构与节点耗能，无法保证网络寿命的最大化。圆形蛛网的螺旋分层结构与有中心分层式无线传感器网络在拓扑形式、结构功能方面有相似之处，其多径性振动信息抗毁传输机理为传感器网络寿命延长提供了一种全新参考。故本文提出一种仿蛛网的FWSN网络寿命优化方法，该方法通过构建流量概率分配机制与负载容量分层模型来有效优化网络寿命。

1 仿蛛网拓扑建构

仿蛛网的农田无线传感器网络拓扑结构模型由节点、径向链路、螺旋链路构成，模型如图1所示。节点散布于监测区域内；径向链路为层间通信最优选择，即相邻层节点间的最短连接路径；螺旋链路为同层通信最佳选择，即同层相邻节点间的最短路径。该拓扑结构中内层节点密度大、覆盖区域小，外层节点密度小、覆盖区域大，具有圆形蛛网的中心收缩聚集特征。

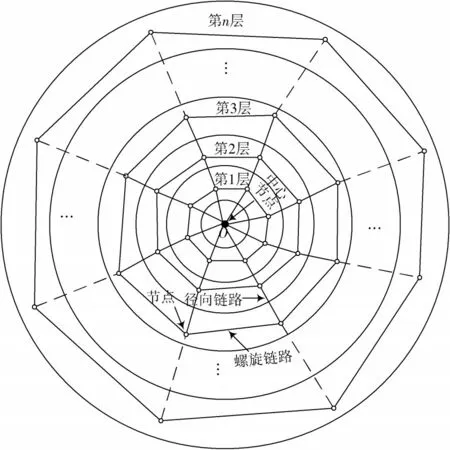
图1 仿蛛网拓扑模型

仿蛛网农田无线传感器网络组网过程是建立网络通信逻辑拓扑的过程，为了便于问题讨论，本文做出如下假设：

1）网络中所有节点都具有唯一的物理坐标，中心节点的物理坐标为（0，0），其他子节点的物理坐标依据与中心节点通信计算得出。

2）任意节点至少可以与1个其他节点通信，即网络中不存在孤立节点，且通信链路为对称链路，即两节点间可实现双向通信。

3）网络采用载波监听多路访问/冲突避免（CSMA/CA）协议，以避免数据传输时发生信道冲突。

具体组网过程如下：

1）中心节点逻辑层默认为0，各子节点路由表初始为空，中心节点广播发送组网数据包，向周围寻找可以建立可靠通信连接的子节点。当周围子节点接收到数据包并计算与中心节点的距离后，此节点成为中心节点的子节点，并将物理坐标添加到本地路由表中。子节点本地路由表格式如表1所示。

表1 子节点本地路由表格式

2）各子节点依据本地路由表中的物理坐标计算与中心节点间的距离以确定自身层号。子节点所在层号编码与中心节点的距离成正相关，即距离中心节点越远，层号越大。层间距可依据实际情况进行自主设定，此时即可获取所有子节点所在的层号，并将层号添加到对应的本地路由表中。层号确定后，将第层子节点以水平方向为起始位置按顺时针分别编码为-1，-2，-3…，由此可以获取所有子节点的分层编号及层节点编号。

3）各子节点层号及物理坐标确定后，首先由逻辑层1内的子节点发送组网帧，显然逻辑层1内的节点既向周围发送组网帧，又会收到来自同层其他子节点的组网帧。收到组网帧的子节点后判断自身层数与源节点的层数关系。

①若两者相等，说明发送方与接收方位于同一逻辑层，则记录两个子节点间的距离，至逻辑层1组网结束时，将所有发送节点中与其通信距离最小的两个子节点作为横向链路节点记录在本地路由表中。

②若接收方层数小于发送方，说明接收方属于较小逻辑层，则仅记录相邻较小逻辑层两子节点间的距离，至逻辑层1组网结束时，将所有发送节点中与其通信距离最小的一个子节点作为径向链路节点记录在本地路由表中。

③若接收方层数大于发送方，则不予处理。

4）重复步骤3），遍历所有逻辑层，组网过程随即完成。

2 流量分配机制

组网结束后，依据所建立的仿蛛网逻辑拓扑建立流量分配机制。

1）任意一个非中心节点，均默认与周围3个子节点建立数据转发关系，即同层的横向链路节点和前一层径向链路节点，并定义选择径向链路和横向链路通信概率分别为，（＞0，＞0且＞），且当任意节点失效时，与其相连的链路同时失效，无法完成数据收发任务，而链路故障时仅使两端节点无法通信。

2）任意节点与所联系的3个子节点间任一节点成功通信的概率均为（0≤≤1）。表2定义了不同工况下节点的通信选择概率和通信成功率。

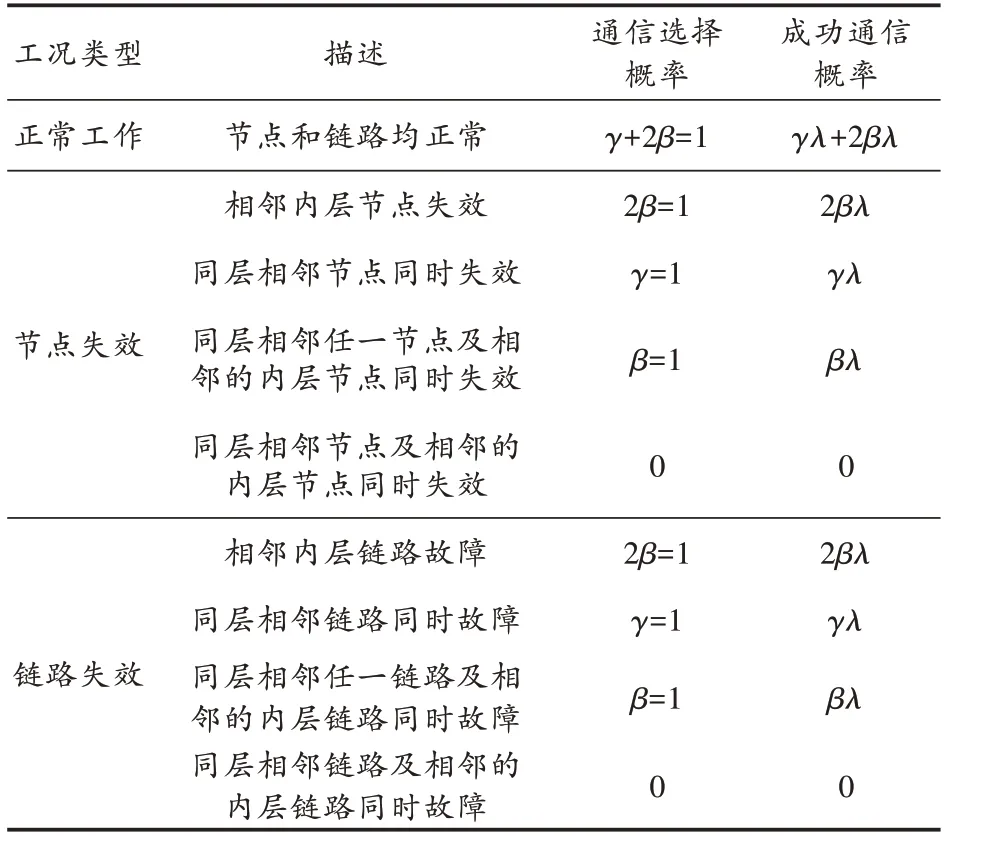
表2 节点通信设定

3）全网子节点与基站通信过程中，若该节点负载超过自身容量，则该节点判定为失效，此时相邻外层节点通过同层中继节点将数据继续向内层节点传输。

4）此外，完成一次迭代后，重新统计剩余存活节点数目，当死亡节点数超过（表示死亡节点与全部节点的比值）时，重新组网形成新的网络拓扑。

Algorithm 1组网通信过程：

3 负载容量分层模型

在经典的负载容量分层模型的基础上，结合仿蛛网FWSN拓扑结构特性，本文提出仿蛛网农田无线传感器网络的负载容量分层模型。

1）基于蛛网分层特征，提出负载容量分层模型如下：

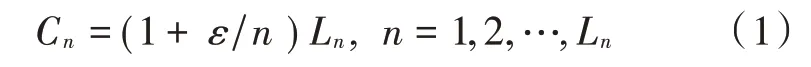
式中：C为第层单个节点容量；L为第层单个节点的初始负载；为调节系数，用于调整节点容量值大小（≥0）；表示层号。

2）第层单个节点的初始负载L定义为：

式中：L表示第层单个节点的初始负载，即同层节点具有一致的初始负载；L表示第+1层所有节点初始负载总和；T表示第层节点总数。内层节点的初始负载取决于相邻外层节点的初始负载，因此，通过定义最外层节点的初始负载便可以获得全网节点的初始负载。负载容量分层模型定义为：

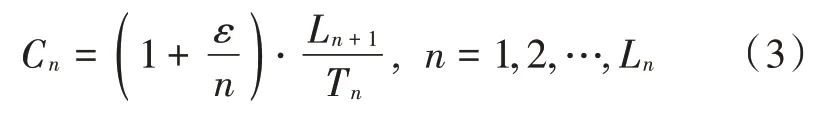
4 网络评价指标

4.1 有效节点比

有效节点比是指网络正常状态的节点数与初始网络中节点数的比值，该指标可从网络失效规模角度评估节点失效对网络的影响，表示为：

式中：N为网络中正常状态节点数；为初始网络的节点数；∈[0，1]。有效节点比越高，表明网络生存能力越佳。

4.2 网络效率比

网络效率是衡量网络级联失效后破坏程度的一个有效指标，网络中两节点之间最短距离的倒数为其对应的网络效率。对于整个网络而言，将所有节点对之间的效率平均值作为网络效率，可用表示，计算公式为：

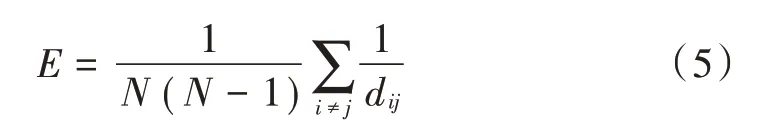
网络效率比为节点失效过程中的网络效率与初始网络效率的比值，其计算公式为：

式中：E为节点失效后的网络效率；∈[0，1]，该指标值越大，表明网络存活能力越好。

5 仿真结果分析

仿蛛网模型仿真环境层数设置为5层，层间距为15 m，根据各层面积占比随机在1~5层节点覆盖区域内生成节点个数12，28，33，48，63，共计184个节点。定义单个节点初始流量（N）为1个标准单位，两节点间通信成功概率设置为0.8，网络仿真环境和参数设置如表3所示。试验结果为50次独立仿真的统计平均结果。

表3 网络仿真参数设置

5.1 性能试验

为分析失效节点数增加时，调节系数对仿真轮数和网络效率比的影响规律，设置随机破坏节点数由5~15变化，调节系数由0~40进行增大，仿真结果如图2所示。从图2a）可以得出，当死亡节点个数在5~15，调节系数由0~40增长时，仿真轮数下降率分别为41.1%，38.2%，35.1%，32.8%，31.8%，31.3%，30.1%，25.4%，23.5%，可以得出，节点故障数增多时，随着调节系数增大，仿真轮数下降率逐渐减小，表明增大调节系数能有效减缓节点失效造成的仿真轮数急剧下降的趋势。当调节系数处于5~40区间，相较于调节系数为0时，平均仿真轮数分别增加了10.7%，16.15%，22.4%，28.3%，35.1%，64.2%，82.3%，93.3%，可知增大调节系数能显著促进网络仿真轮数的增加，当调节系数大于等于30时，网络仿真轮数增速要显著大于调节系数小于30时，表明数值较大的调节系数能有效延长网络寿命。

从图2b）可以看出，当死亡节点个数由5~15，调节系数由0~40变化时，网络效率比下降率分别为27.0%，25.6%，5.5%，25.9%，23.7%，23.6%，23.0%，23.5%，21.8%，表明节点故障数增多时，调节系数增大与网络效率比下降呈负相关关系。当死亡节点个数由5~15，调节系数为5~40变化，相较于调节系数为0时，平均网络效率比分别增加了19.9%，24.8%，54.3%，62.1%，70.9%，120.2%，139.2%，168.4%，可以得出，网络效率比随调节系数增大而提高；当调节系数大于等于30时，网络效率比增速要大于调节系数小于30时，表明调节系数增大对提升网络效率比具有积极作用。

图2 调节系数对仿真轮数和网络效率比的影响

为分析该网络寿命优化方法在应对不同位置节点故障时的表现，对模型中每一层节点进行随机故障攻击，仿真结果如表4所示。

从表4可以看出，第1~5层随机2个节点失效时，随着调节系数的增加，仿真轮数和网络效率比均显著增加，如当死亡节点占比为0.9，调节系数由0增加到40时，第1~5层仿真轮数分别增加48.9%，37.6%，39.75%，38.9%，22.1%，网络效率比分别增加19.1%，24.7%，23.6%，23%，50%，表明调节系数对仿真轮数和网络效率比均具有显著的提升效果，但调节系数对仿真轮数和网络效率比的影响程度由内层到外层分别为逐渐减弱和渐趋增强的趋势。其中，当死亡节点占比为0.9时，第1~5层不同调节系数下的平均仿真轮数分别为156.26，154.36，151.12，154.76，99.96轮，平均网络效率比分别是0.050，0.049，0.047，0.046，0.056。

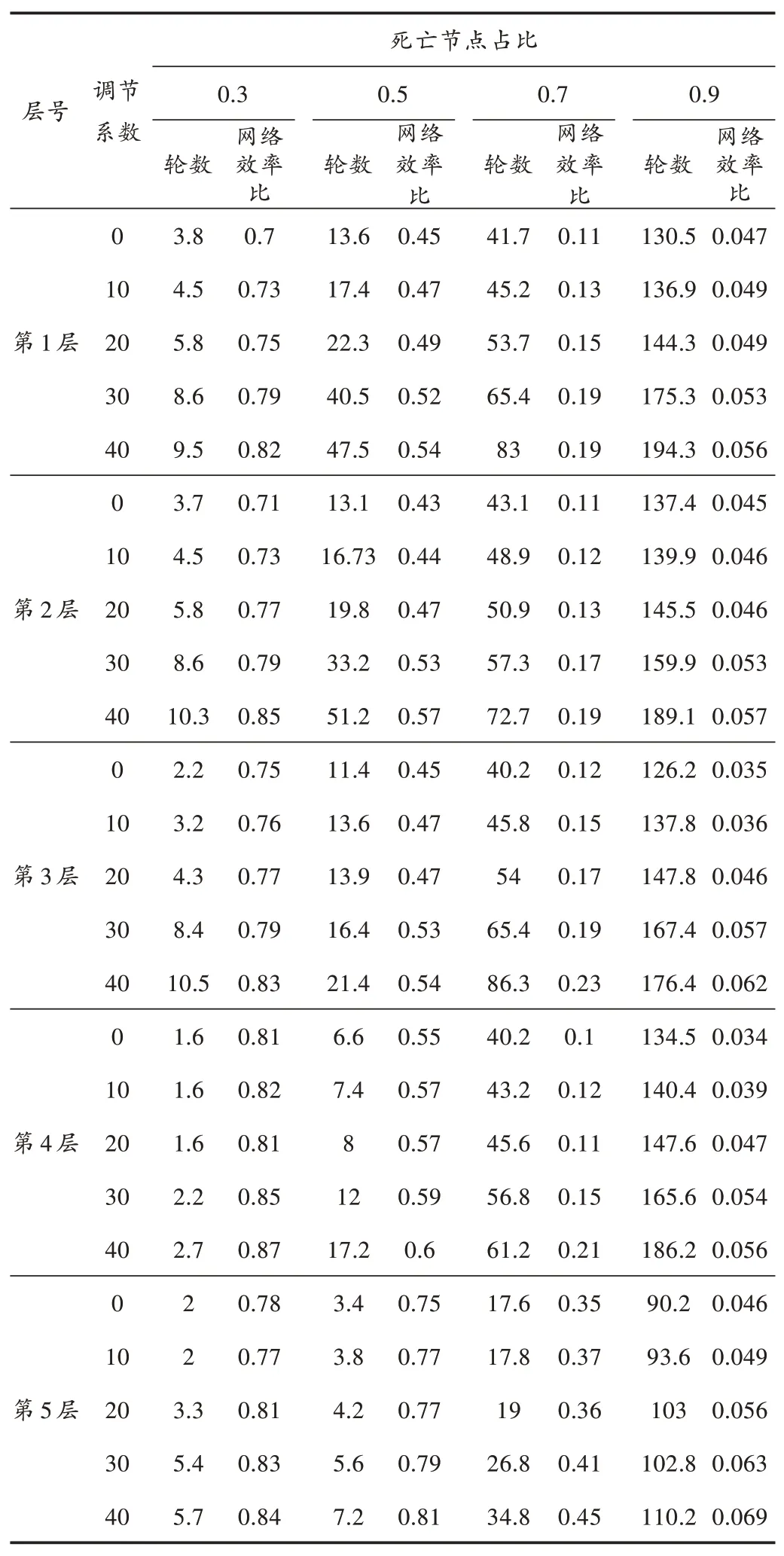
表4 第1~5层随机2个节点失效时的网络性能

由此说明，内层节点失效时，通过调整调节系数可有效增强网络的抗毁能力，边缘位置节点的失效相较于内层节点的影响效果相对较弱。

以上仿真结果表明，本文所提出的网络寿命优化方法可合理调度部分节点失效后的网络流量，并通过节点的初始能量由外层至内层关联性增加，有效地降低不同层节点重要性差异所带来的能耗差异，从而保障网络连通度水平，均衡全网节点能耗，可靠延长FWSN网络寿命。

5.2 对比试验

为进一步测试本文提出的网络寿命优化方法的性能，采用城市轨道交通网络级联失效模型与本文算法进行对比试验，得到的仿真结果如图3所示。图3a）为选择性失效和随机性失效方式下两种算法的有效节点比随仿真轮数增加的变化规律。从图3a）可以看出：当仿真轮数为5时，4类情况下有效节点占比分别为0.4，0.75，0.97，0.98；随着仿真轮数继续增加至10时，4类情况下有效节点比分别为0.25，0.68，0.9，0.93，相较于5轮时分别下降37.5%，9.3%，9.2%，8.1%。可知，本文所提的算法在选择性失效和随机性失效情况下，有效节点比随仿真轮数变化趋势一致且变化幅度相近，能有效延长网络寿命。

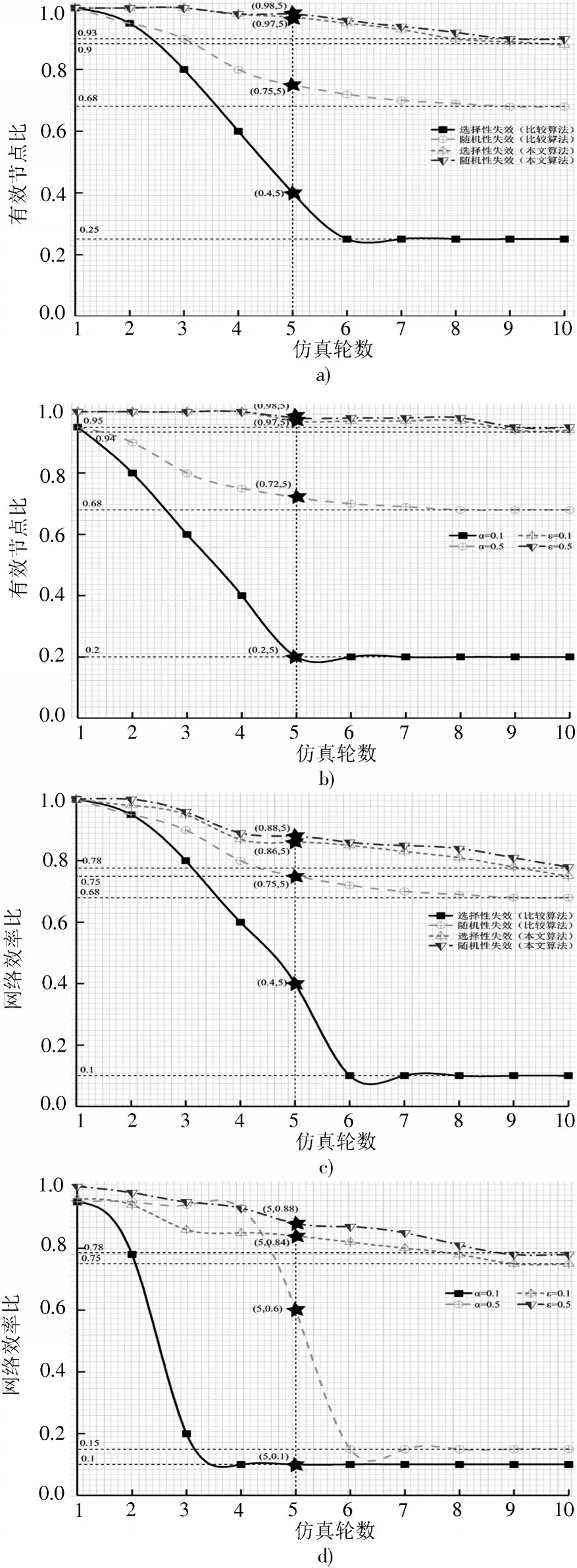
图3 网络评价/指标比较

图3b）为选择性失效情况下，两种算法在不同调节系数下有效节点比随仿真轮数增加的变化规律。从图3b）可以看出，当仿真轮数为5时，，分别由0.1增加至0.5时，有效节点比分别增加260%和1.0%。此外，为0.1时的有效节点比是为0.5时的1.3倍。可知通过增大调节系数，比较算法的有效节点比显著增大，而本文所提算法表现出缓慢的增长趋势，但此时本文所提算法下的有效节点比仍远高于比较算法，这是由于本文算法的负载容量调整与网络分层紧密相关，分配策略更加合理。图3c）为两种算法在不同的失效方式下网络效率比的变化规律。从图3c）可以看出：当仿真轮数为5时，4类情况下网络效率比分别是0.4，0.75，0.86，0.88；随着仿真轮数继续增加到10时，4类情况下网络效率比分别是0.1，0.68，0.75，0.78，相较于5轮时分别下降75.0%，9.3%，12.7%，11.3%。可以发现，本文所提的算法在选择性失效和随机性失效情况下，网络效率比均能表现出一致的变化规律，且变化趋势平缓。图3d）为选择性失效情况下，两种算法在不同调节系数下网络效率比的变化规律。从图3d）可以看出：当仿真轮数小于5时，比较算法通过增大调节系数可有效延缓网络效率比的下降，当仿真轮数继续增加时，即使增大调节系数，网络效率比仍维持在较低的水平；而本文所提模型在调节系数较小时，网络效率比即可保持较高水平，随着调节系数的增加，网络效率比具有增长趋势，但增幅较小。

通过上述分析可知，本文所提仿蛛网的FWSN网络寿命优化方法可在面对节点不同类型失效时动态调度网络流量，依据节点所在层合理分配容量，可靠保证网络联通度，均衡网络能耗，使得有效节点比和网络效率比均能稳定变化且变化幅度缓慢，最大化提高网络寿命。

6 结 语

受自然界圆形蛛网抗毁结构启示，本文提出一种仿蛛网的网络寿命优化方法，该方法由流量概率分配机制与负载容量分层模型组成。仿真实验结果表明，增大调节系数可促进网络仿真轮数和网络效率比的增加，当调节系数大于等于30时，网络仿真轮数和网络效率比增速显著大于调节系数较小的情况。相较于对比算法，流量概率分配机制能动态调度网络流量以减少节点失效对网络连通度的影响，负载容量分层模型可有效平衡不同层节点的能耗差异。此外，本文所提出的网络寿命优化方法在选择性失效和随机性失效情况下，均能有效减缓有效节点比和网络效率比的下降趋势，确保农田无线传感器网络的可靠性，为改善农田无线传感器网络存活时间提供一种新的解决思路。