基于参数优化变分模态分解的间谐波检测
2022-06-13郑晓娇李卜娟
郑晓娇,王 斌,李卜娟,喻 敏
基于参数优化变分模态分解的间谐波检测
郑晓娇1,王 斌1,李卜娟1,喻 敏2
(1.武汉科技大学信息科学与工程学院,湖北 武汉 430081;2.武汉科技大学理学院,湖北 武汉 430065)
变分模态分解(VMD)已在谐波检测领域得到应用,但人为设定分解参数,导致误差较大。为提升VMD在间谐波检测中的准确性,首先,采用施密特正交化理论对VMD预分解得到的各分量进行正交化处理,以避免模态混叠。然后求得不同值对应的残差能量,利用残差能量值最小化法优化参数,进而提取间谐波信号。最后采用对称差分能量算子,获得间谐波信号幅值与频率等特征信息。仿真实验表明:所提出的方法能有效优化参数,降低VMD分解误差。同经验模态分解(EMD)、集合经验模态分解(EEMD)以及近年新提出的同步挤压小波变换(SST)相比,参数优化变分模态分解在间谐波检测上效果显著提升,具有更高的检测精度。
间谐波;变分模态分解;施密特正交化;残差能量;对称差分能量算子
0 引言
近年来大量新型非线性电力电子设备以及非线性负荷等投入到电力系统中,严重影响电力设备的工作稳定性以及优质电能的产生,其中以谐波问题最为突出[1-4]。谐波对电力系统的危害巨大[5],而电力系统中不仅存在整数次谐波,也存在非整数次谐波,即间谐波。间谐波的危害远大于整数次谐波,因此对电力系统中存在的间谐波进行治理很有必要,而能准确检测间谐波是治理的前提[6-8]。
检测间谐波的常用方法有傅里叶变换[9-10]、小波变换[11-12]、希尔伯特黄变换(Hilbert-Huang Transform, HHT)[13]、同步挤压小波变换(Synchrosqueezing wave-let Transform, SST)[14]等。傅里叶变换能准确提取信号中的整数次谐波分量,然而由于电力信号中的间谐波与基波并非同步变化,导致其波形周期难以确定,因而采用傅里叶变换提取间谐波时,易产生由于非同步采样而导致的“栅栏效应”和“频谱泄露”[15]等问题,使检测结果不准确。小波变换作为傅里叶变换思想的拓展与延伸,它能够解决傅里叶变换因非同步采样而引起的“栅栏效应”和“频谱泄露”问题,且还能自由调节时频窗,具有较强的自适应性,但其需预先设置小波基与分解层数[16],而不同的小波基对间谐波的检测效果影响较大。不仅如此,在分解过程中,小波变换仅能对信号的低频部分进行分解,而无法分解高频部分,使间谐波检测精度在整体上降低。HHT是近年来分析非线性复杂波形中性能较好的时频工具,它由经验模态分解(Empirical Mode Decomposition, EMD)和希尔伯特变换(Hilbert Transform, HT)两部分构成。HHT首先采用EMD将输入信号分解为一系列本征模态函数,再运用HT求得各分量的幅值与频率,因其无需选择基函数且能自适应分解,近年来已被广泛应用于电力谐波以及间谐波信号的检测中,然而EMD在分解过程中易引入虚假分量,不仅如此,它还会造成模态混叠和端点效应等问题,同时,HT产生的负频率目前也无法解释。SST是以连续小波变换(Continuous Wavelet Transform, CWT)为基础的时频分析方法,它通过在频域方向上对CWT系数进行同步挤压,降低了各时频曲线发生交叉的可能,具有良好的模态分解能力以及抗噪性,是近年来新出现的检测间谐波精度很高的方法。但其在利用CWT进行同步挤压处理时,同小波变换一样,需选择合适的小波母函数,且同步挤压的效果会受到该选择的较大影响[17]。
变分模态分解[18](Variational Mode Decomposition, VMD)是信号处理中一种较新的时频分析方法,近年来已有学者将其应用于谐波检测领域。文献[19]首次将VMD用于电力谐波信号的检测中,有较好的检测效果,但就值如何选取并未明确说明。文献[20]运用频谱预分析的方法来确定VMD分解模态数,但其需要人为观察频谱个数,且在电力信号检测中未考虑间谐波的影响。事实上采用VMD对信号间谐波成分检测时,模态数对检测效果的影响很大。若值选取不当,VMD易出现过分解、欠分解现象,导致VMD对间谐波的检测效果受到影响。因此为了实现变分模态分解对间谐波信号的准确提取,本文提出了一种优化VMD算法中参数的间谐波检测方法,并应用对称差分能量算子求解幅值和频率参数。仿真表明:该方法有效解决了VMD中参数需人为设定的问题,参数优化效果好,能正确提取出信号中所包含的间谐波成分,实现间谐波信号的高精度检测。
1 变分模态分解
变分模态分解是一种完全非递归的模态变分和信号处理方法。其主要运用了维纳滤波、希尔伯特变换以及频率混合的原理。它重新定义了本征模态函数(Intrinsic Mode Function, IMF),认为每一个IMF是一个调幅-调频(AM-FM)信号,如式(1)所示。




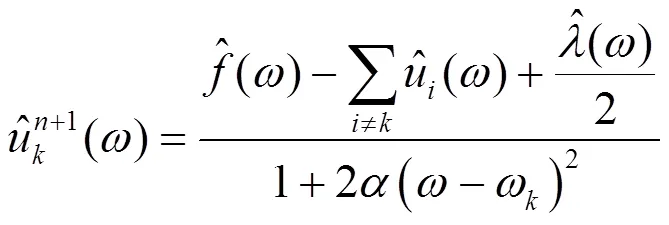


VMD算法具体的实现过程如下。
2 基于参数优化VMD的间谐波检测
2.1 不同K值对VMD分解性能的影响
VMD对非平稳、非线性信号具有良好的分解效果。但同许多经典聚类和分段算法(如K-means)一样,其分解效果受参数选取的影响较大。如果分解参数设置不合理,则会导致分解结果出现较大误差。
由VMD的约束条件可知,VMD分解的本质是使得输入信号近似等于个模态之和,因而当过小时,易导致信号分解不足,信号中的部分分量混在一起,呈现欠分解状态。而过大则会使得信号分解过度,信号的重要部分由两个或多个不同的模式共享,并且它们的中心频率重合,呈现过分解状态。因此在使用VMD进行信号分解时,需预先确定合适的值。
为更直观地说明,给定信号如式(7)所示,取不同值时,对该信号进行VMD分解,分解结果如图1所示。


由图1可知,=2时,IMF1中明显混有多个频率分量,导致波形畸变,说明过小,信号未被完全分解;=5时,IMF2—IMF4频率相同,均为24 Hz,说明过大,导致一个信号成分被分解为多个,信号被过度分解。由此可知,值不同,得到的结果差异很大。
2.2 基于残差能量值优化参数K
在使用模式和重构输入信号的约束下,VMD能同时从原信号中提取出多种模式,但其忽略了残差(即输入信号与重构信号之间的差异)对算法性能的影响[21]。因此,本文将变分模态分解过程中的残差考虑进来,用以优化参数。

又因VMD分解得到的分量并非完全正交[22],导致可能出现模态混叠。因此,对VMD预分解得到的个分量采用施密特正交化理论进行处理,剔除分量间相关成分。正交化处理后各分量如式(9)所示。


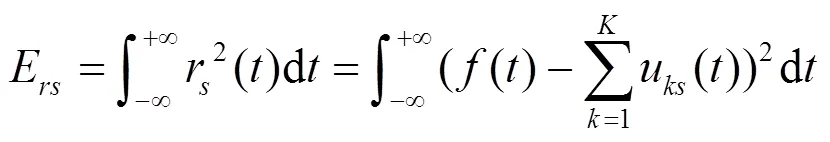

为更好地说明对分量进行施密特正交化处理以及利用残差能量值最小化优化参数的意义,以式(7)为例对其进行直观展示,图2是将图1正交化后的结果。
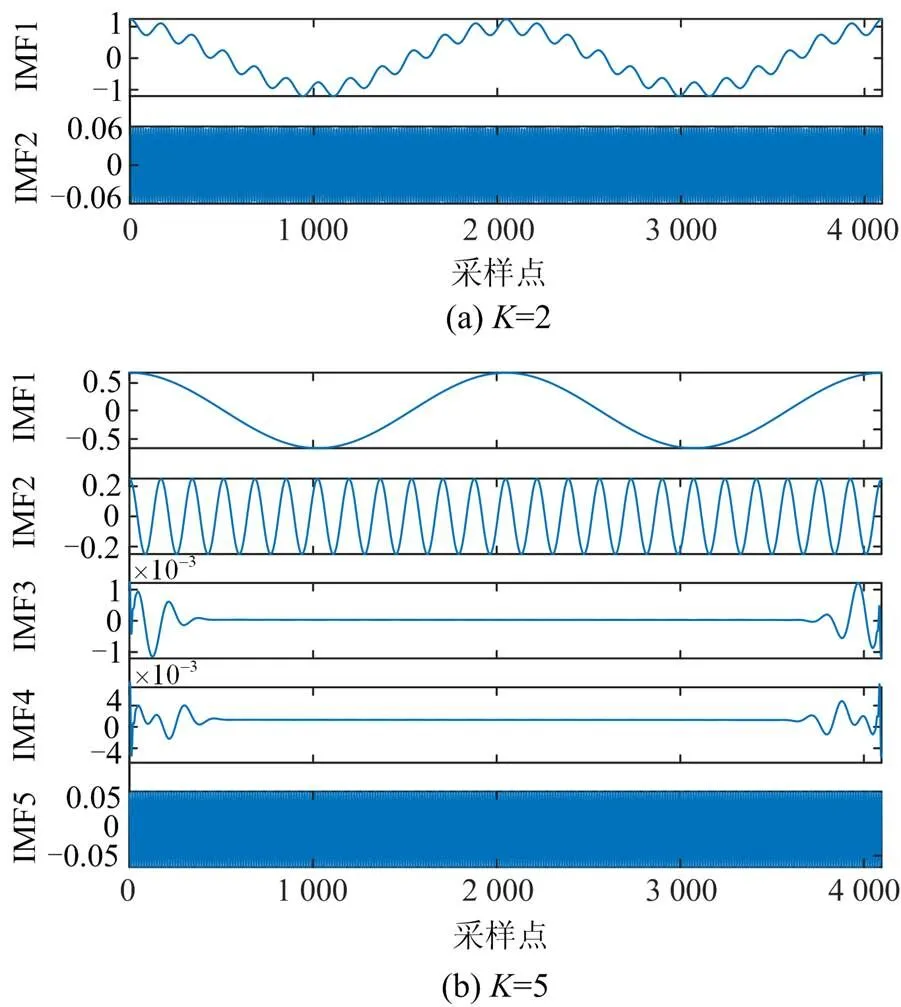
图2 不同K值下正交后信号分解图
由图2可知,较小时,分量中基本无相关性较大成分,只是不同频率成分未被完全分解,正交化处理对其影响较小,剔除的分量较少,基本与正交化前一致。而过大时,因IMF2—IMF4相关,正交化处理后,IMF3和IMF4中与IMF2相关的成分被剔除,基本变为0。

2.3 对称差分能量算子
对称差分能量算子[23]在Teager能量算子(Teager Energy Operator, TEO)[24]的基础上推导而来。为减小TEO解调时带来的误差,对称差分能量算子采用中心有限差分代替TEO中的前向差分,则信号()的差分序列变为

在原始离散信号的基础上对信号进行平滑处理,则可以得到平滑后的差分序列为
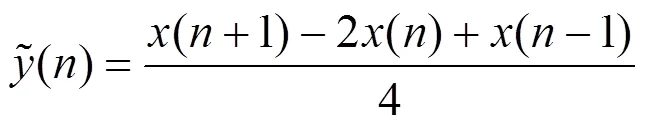
对式(13)进行能量算子运算,可得
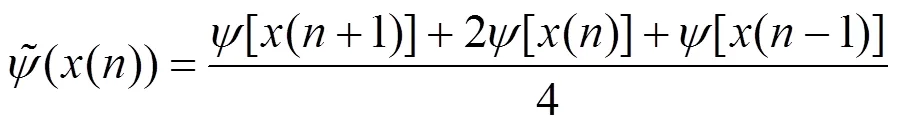


3 仿真与实测数据分析
3.1 算例1:稳态间谐波分析
电力系统中含间谐波的稳态仿真信号模型可表示为



由图4可知,VMD分解得到的IMF2—IMF7都呈规则的正弦波动,未发生畸变,说明其为单一分量,且其能与原始信号中的6个分量一一对应,说明参数优化后的VMD方法能将原始信号中的各分量信号分解出来,得到合理的分解结果。图5对应的EMD分解中仅IMF1与IMF3能很明显地判断其为5次谐波和基波分量,其余原始信号中的间谐波成分均未分解出来。图6中EEMD亦是仅能识别出基波与5次谐波,而无法识别间谐波分量。EMD与EEMD无法分离出间谐波成分是由于原始信号中的间谐波均相隔较近,而EMD与EEMD能将分量分离开的条件是较大分量与较小分量的频率比值大于2[26],显然原始信号中的间谐波分量并未满足此条件,因而EMD及EEMD方法无法将其分解出来。同时,从图6中可以看出,EMD与EEMD分解出的分量中产生了大量虚假分量,会影响判断,虽VMD分解也会产生虚假分量,但远少于EMD与EEMD。不仅如此,其产生的虚假分量基本为零,能很好地将虚假分量与真实分量区分开来,从而不影响判断。从图7可以看出,SST分解仅前两项能对应原始信号中的分量,但其分解效果明显好于EMD和EEMD分解。分量1为基波,分量2为5次谐波,所得到的基波分量与谐波分量均未出现模态混叠现象。但与参数优化VMD分解相比,SST未将原始信号中的间谐波分量分解出来。虽然SST将分解得到的时频图在频率域方向进行了压缩,能够有效避免频率混叠,在检测较为接近的间谐波频率时有一定优势,但当有多个相邻的频率较为接近的间谐波成分时,SST仍无法检测出。

图3 稳态信号残差能量值变化

图4 稳态信号及其VMD分解

图5 稳态信号EMD分解

图6 稳态信号EEMD分解

图7 稳态信号SST分解
运用对称差分能量算子对VMD分解得到的各分量进行解调,并求其瞬时幅值与频率平均值,得检测结果如表1所示。
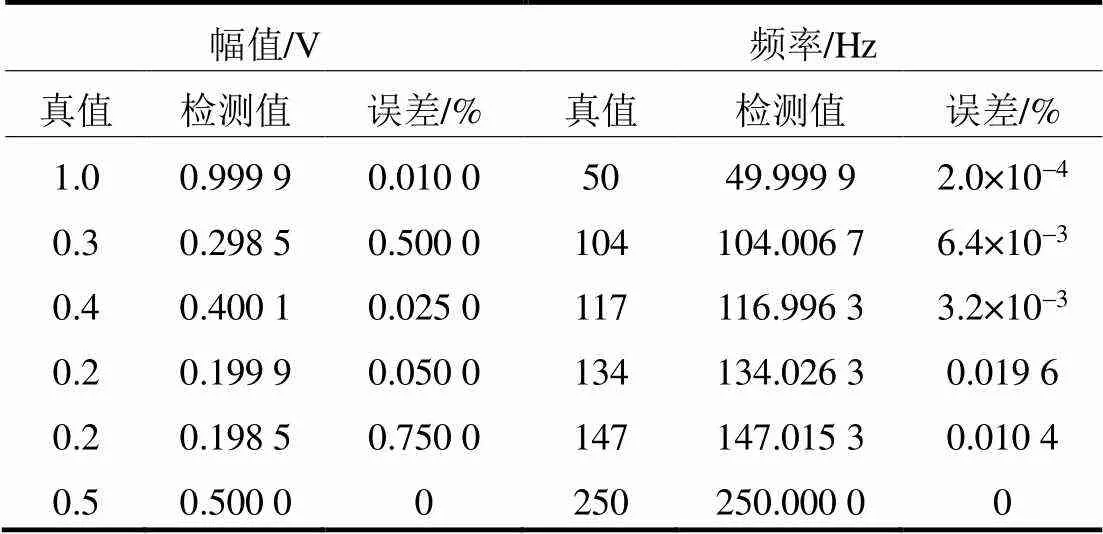
表1 稳态信号检测结果
由表1稳态信号的检测结果可知,检测出的各分量幅值与频率都很精确,检测误差小,与真实值接近。
以上检测结果说明:当电力信号中存在有较为接近的间谐波分量时,本文所提出的参数优化方法适用且有效,参数优化VMD能将各分量信息都准确提取出来,且具有较高的检测精度。
3.2 算例2:时变间谐波信号分析
在实际电力系统中,间谐波的幅值与频率往往具有时变的特点,因此将参数优化后的VMD运用于时变间谐波信号的检测,设含时变间谐波的信号如式(19)所示。

考虑在时变信号中加入信噪比为50 dB的高斯白噪声干扰,采样频率与采样点数均与算例1一致。
图8是对该时变信号采用VMD及施密特正交化进行预处理后的残差能量值变化图。由图8可知,= 7时对应的残差能量最小,因此,将= 7作为VMD方法分解时变间谐波信号的最优值。

图8 时变信号残差能量值变化
图9—图12分别为VMD、EMD、 EEMD以及SST分解结果。

图9 时变信号及其VMD分解

图10 时变信号EMD分解
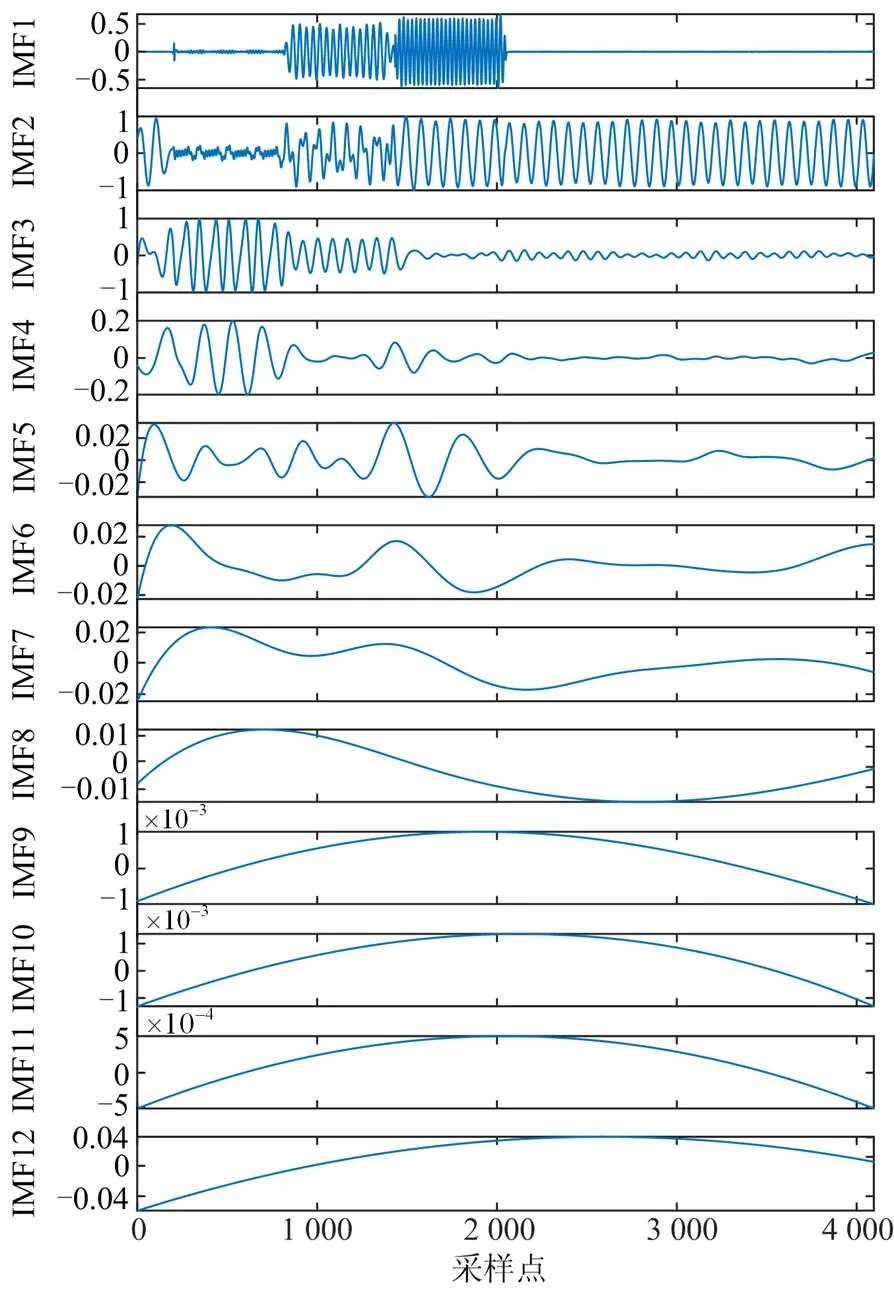
图11 时变信号EEMD分解
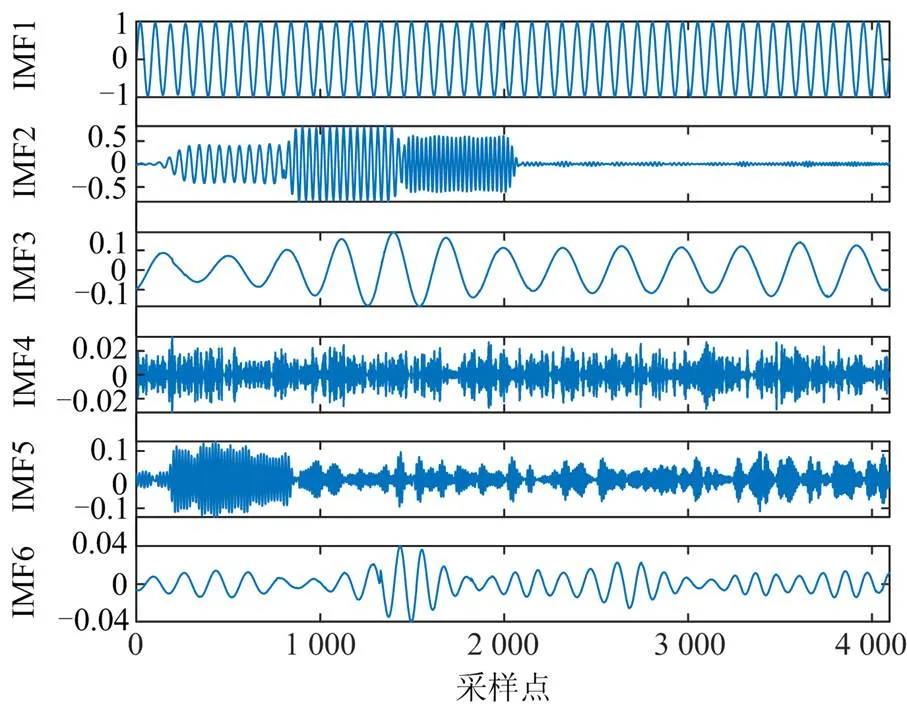
图12 时变信号SST分解
由图9可知,VMD方法分解出的前5项可以对应原始时变信号中的各分量。其中IMF1对应时变信号中的基波,IMF2与IMF5分别对应0.05~0.2时段75 Hz间谐波和5次谐波,IMF3对应0.2~0.35时段110 Hz间谐波,IMF4对应0.35~0.5时段175 Hz间谐波,可见VMD方法将每一时段的分量均分离了出来。图10中,EMD分解出的IMF1从左到右依次对应原始信号中的5次谐波,110 Hz间谐波以及175 Hz间谐波,IMF2为基波,IMF3为75 Hz间谐波,但其幅值明显变小,且基波与75 Hz间谐波产生了模态混叠现象。图11中EEMD能分辨出IMF1为110 Hz和175 Hz间谐波,IMF2为基波,IMF4对应75 Hz间谐波,但分量与分量间模态混叠严重,如理应在IMF2中的基波有部分出现在了IMF3中。由此可见,EMD与EEMD分解出的分量均出现了不同程度的模态混叠现象。由图14可知,SST分解得到的IMF1为基波,IMF2分别对应原始时变信号中的0.05~0.2、0.2~0.35、0.35~0.5这三个时段信号,其分别为75 Hz、110 Hz及175 Hz间谐波,可见SST将时变信号中的间谐波成分均分解了出来,效果与VMD相当,第5分量的前面部分对应原始信号中0.05~0.2时段的5次谐波,但其发生了严重畸变,且其与信号中的噪声混合,容易将其误判为噪声分量,而无法检测出来。
3.3 算例3:实际含间谐波的信号分析
文献[27]建立了一台三相电弧炉谐波电流模型,本文引用其熔化模式下的电弧炉稳态电流数据,并设置采样频率为4 096 Hz,采样4 096点,同时在原始电弧炉数据中加入5%的随机噪声,该电弧炉信号将60 Hz作为基波频率。

图13 实际电弧炉信号残差能量值变化
采用VMD及施密特正交化理论预处理电弧炉信号,得到其残差能量值变化如图13所示,从图13可知,= 7时对应的残差能量最小,因此将= 7作为VMD的最佳分解参数。电弧炉信号的VMD分解以及EMD、EEMD、SST分解结果如图14—图17所示。
图14中VMD分解得到的IMF2—IMF7均为规则的正弦信号,由此可知这6个分量均为电弧炉电流信号中的各成分。而图15中的EMD分解只得到了2个分量,图16中EEMD分解可以得到12个分量,但均发生了不同程度的模态混叠,无法对各个分量进行识别。而图17中SST得到的分解图仅前4个分量为规则无畸变的正弦信号分量,说明其仅分解出了4个分量。运用对称差分能量算子求VMD分解所得的各分量的瞬时幅值与瞬时频率,并对其求平均值,得幅值与频率的检测结果如表2所示。

图14 电弧炉信号及其VMD分解

图15 实际电弧炉信号EMD分解
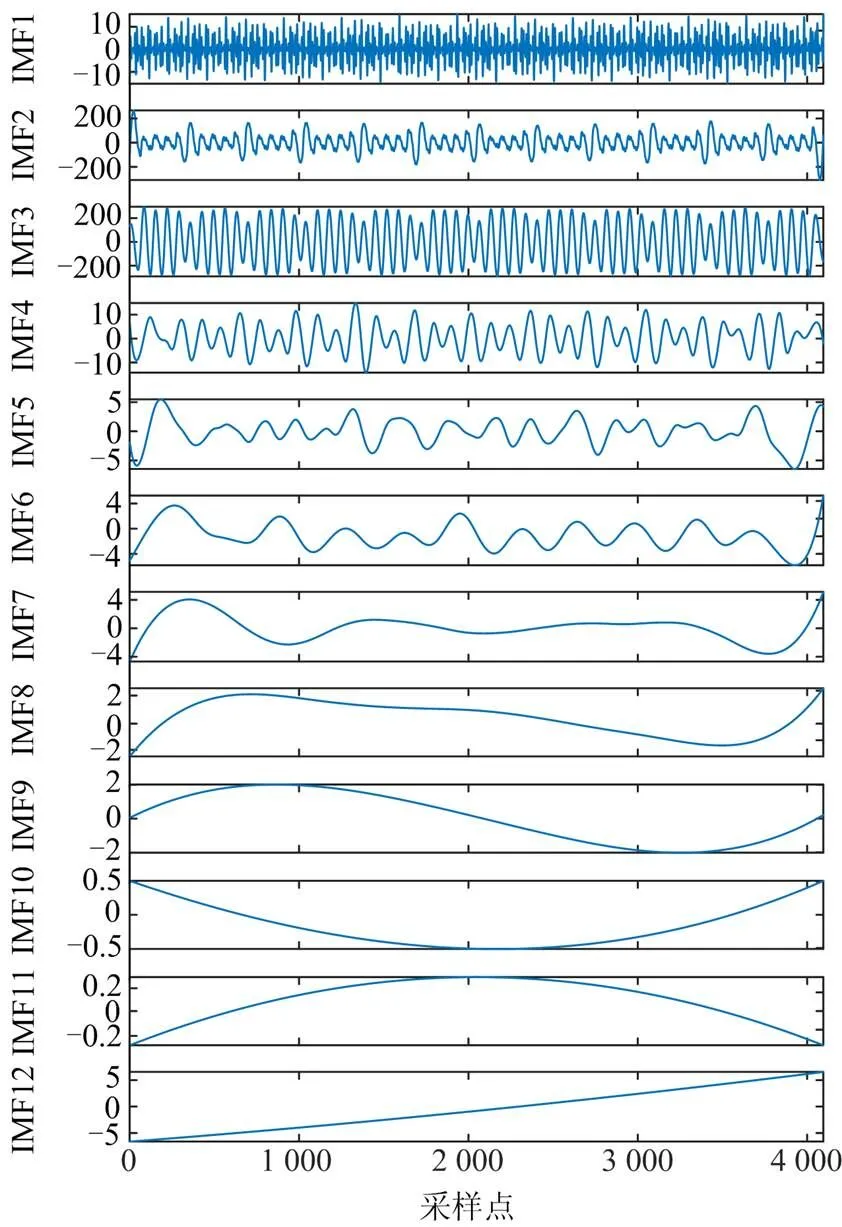
图16 实际电弧炉信号EEMD分解

图17 实际电弧炉信号SST分解

表2 电弧炉信号检测结果
由表2可知,VMD方法检测出了电弧炉信号中的所有分量成分,且检测结果均接近真值,幅值检测误差与频率检测误差均较小,都满足电力系统间谐波检测的要求。
4 结语
针对VMD中参数需人为设定的问题,本文提出了一种参数优化变分模态分解的方法。利用VMD分解信号的能力将电力信号中的间谐波有效分离出来,并结合对称差分能量算子提取间谐波幅值与频率,实现了对电力系统中稳态以及暂态间谐波信号的检测。通过分析与实验验证,得出了以下结论。
(1) 运用残差能量最小化优化参数的方法,有效解决了传统变分模态分解算法中值需人为设定的问题,实现了信号最优分解。
(2) 参数优化变分模态分解与对称差分能量算子相结合的方法能有效检测出电力信号中频率较为接近的间谐波成分,效果好于传统的EMD、EEMD、SST分解,且有较高的检测精度,适用于稳态、暂态间谐波信号的检测。
(3) 参数优化后,变分模态分解得到的虚假分量远少于EEMD分解,且虚假分量基本为零,能与真实分量区分开来,大大降低了发生误判的可能。
本文在理论分析中验证了所提方法的准确性与有效性。实际运用中,可考虑利用CCS9.2.0平台实现文中所提算法,后将编译结果抄写至C2000系列DSP运行,检测结果通过DA模块模拟输出信号或通过串口输出至上位机平台,实现电力信号的检测与分析。但本文方法并未考虑强噪声环境以及间谐波接近基波分量的影响,因而还需进一步深入研究,拓展该方法的适用性,为实际应用提供更有利的支持。
[1] 兰金晨, 朱革兰, 李松奕. 基于广义S变换突变识别的暂稳态谐波检测方法[J]. 电力系统保护与控制, 2020, 48(23): 40-46.
LAN Jinchen, ZHU Gelan, LI Songyi. Detection method of transient and steady state harmonics based on generalized S-transform mutation recognition[J]. Power System Protection and Control, 2020, 48(23): 40-46.
[2] AMROUNE M, BOUKTIR T, MUSIRIN I. Power system voltage instability risk mitigation via emergency demand response-based whale optimization algorithm[J]. Protection and Control of Modern Power Systems, 2019, 4(1): 1-14.
[3] 袁丽丽, 阳育德, 覃智君, 等. 基于谐波阻抗特性的风电次同步振荡分析[J]. 电力建设, 2020, 41(4): 117-125.
YUAN Lili, YANG Yude, QIN Zhijun, et al. Analysis of sub-synchronous oscillation in wind farm according to harmonic impedance characteristics[J]. Electric Power Construction, 2020, 41(4): 117-125.
[4] 王泽忠, 王欢, 杨萧箫, 等. 基于轴对称模型的特高压变压器直流偏磁分析[J]. 高压电器, 2020, 56(4): 87-94.
WANG Zezhong, WANG Huan, YANG Xiaoxiao, et al. DC magnetic bias analysis of uhv transformer based on axisymmetric model[J]. High Voltage Apparatus, 2020, 56(4): 87-94.
[5] 夏家辉, 方园, 刘卜瑞, 等. 基于特征电流波宽判据的变压器差动保护方法[J]. 电力工程技术, 2020, 39(1): 184-190.
XIA Jiahui, FANG Yuan, LIU Burui, et al. The transformer differential protection method based on characteristic current waveform width criterion[J]. Jiangsu Electrical Engineering, 2020, 39(1): 184-190.
[6] 林才华, 张逸, 邵振国, 等. 用于低频非平稳间谐波研究的超高功率电弧炉模型[J]. 中国电力, 2020, 53(11): 1-8.
LIN Caihua, ZHANG Yi, SHAO Zhenguo, et al. An ultra-high-power electric arc furnace model for low-frequency non-stationary inter-harmonics studies[J]. Electric Power, 2020, 53(11): 1-8.
[7] 吴建章, 梅飞, 陈畅, 等. 基于经验小波变换的电力系统谐波检测方法[J]. 电力系统保护与控制, 2020, 48(6): 136-143.
WU Jianzhang, MEI Fei, CHEN Chang, et al. Harmonic detection method in power system based on empirical wavelet transform[J]. Power System Protection and Control, 2020, 48(6): 136-143.
[8] 陶顺, 郭傲, 刘云博, 等. 基于矩阵束和奇异值分解的间谐波检测算法[J]. 电力系统保护与控制, 2021, 49(2): 57-64.
TAO Shun, GUO Ao, LIU Yunbo, et al. Interharmonic detection algorithm based on a matrix pencil and singular value decomposition[J]. Power System Protection and Control, 2021, 49(2): 57-64.
[9] 钱昊, 赵荣详. 基于插值FFT算法的间谐波分析[J]. 中国电机工程学报, 2005, 25(21): 87-91.
QIAN Hao, ZHAO Rongxiang. Interharmonic analysis based on interpolation FFT algorithm[J]. Proceedings of the CSEE, 2005, 25(21): 87-91.
[10] 房国志, 杨才山, 杨超. 基于Meyer小波和FFT的电网间谐波检测[J].电力系统保护与控制, 2011, 39(12): 90-93, 101.
FANG Guozhi, YANG Caishan, YANG Chao. Detection of inter-harmonic in power system based on Meyer wavelet and FFT[J]. Power System Protection and Control, 2011, 39(12): 90-93, 101.
[11] DIEGO R I, BARROS J. Global method for time-frequency analysis of harmonic distortion in power system using the wavelet packet transform[J]. Electric Power Systems Research, 2009, 79(8): 1226-1339.
[12] 杨名, 陈红卫. 一种基于小波包和apFFT的间谐波检测方法[J]. 电力系统保护与控制, 2017, 45(15): 112-117.
YANG Ming, CHEN Hongwei. A method to detect inter-harmonics based on wavelet packet and apFFT[J]. Power System Protection and Control, 2017, 45(15): 112-117.
[13] 张宇辉, 贺健伟, 李天云, 等. 基于数学形态学和HHT的谐波和间谐波检测方法[J]. 电网技术, 2008, 32(17): 46-51.
ZHANG Yuhui, HE Jianwei, LI Tianyun, et al. A new method to detect harmonics and inter-harmonics based on mathematical morphology and Hilbert-Huang transform[J]. Power System Technology, 2008, 32(17): 46-51.
[14] 喻敏, 王斌, 王文波, 等. 基于SST的间谐波检测方法[J]. 中国电机工程学报, 2016, 36(11): 2944-2951.
YU Min, WANG Bin, WANG Wenbo, et al. An inter-harmonics detection method based on SST[J]. Proceedings of the CSEE, 2016, 36(11): 2944-2951.
[15] 惠锦, 杨洪耕. 基于间谐波泄漏估算的谐波间谐波分离检测法[J]. 电工技术学报, 2011, 26(1): 183-190.
HUI Jin, YANG Honggeng. Harmonics and interharmonics separate: detection method based on estimation of leakage values caused by interharmonics[J]. Transactions of China Electrotechnical Society, 2011, 26(1): 183-190.
[16] 唐忠, 焦婷. 基于小波包变换的电力系统谐波分析[J]. 电测与仪表, 2016, 53(18): 57-62.
TANG Zhong, JIAO Ting. Power system harmonic analysis based on wavelet packet transform[J]. Electrical Measurement & Instrumentation, 2016, 53(18): 57-62.
[17] 童涛, 张新燕, 刘博文, 等. 基于傅里叶同步挤压变换和希尔伯特变换的谐波间谐波检测分析[J]. 电网技术, 2019, 43(11): 4200-4208.
TONG Tao, ZHANG Xinyan, LIU Bowen, et al. Analysis of harmonic and inter-harmonic detection based on Fourier-based synchrosqueezing transform and Hilbert transform[J]. Power System Technology, 2019, 43(11): 4200-4208.
[18] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.
[19] 陈强伟, 蔡文皓, 孙磊, 等. 基于VMD的谐波检测方法[J]. 电测与仪表, 2018, 55(2): 59-65.
CHEN Qiangwei, CAI Wenhao, SUN Lei, et al. Harmonic detection method based on VMD[J]. Electrical Measurement & Instrumentation, 2018, 55(2): 59-65.
[20] 陈陈, 李晓明, 杨玲君, 等. 变分模态分解在电力系统谐波检测中的应用[J]. 电力系统保护与控制, 2018, 46(14): 63-70.
CHEN Chen, LI Xiaoming, YANG Lingjun, et al. Application of variational mode decomposition in power system harmonic detection[J]. Power System Protection and Control, 2018, 46(14): 63-70.
[21] LI J, CHENG X, LI Q, et al. Adaptive energy-constrained variational mode decomposition based on spectrum segmentation and its application in fault detection of rolling bearing[J]. Signal Processing, 2021, 183.
[22] 许子非, 岳敏楠, 李春. 优化递归变分模态分解及其在非线性信号处理中的应用[J]. 物理学报, 2019, 68(23): 292-305.
XU Zifei, YUE Minnan, LI Chun. Application of the proposed optimized recursive variational mode decomposition in nonlinear decomposition[J]. Acta Physica Sinica, 2019, 68(23): 292-305.
[23] 孟宗, 李姗姗, 季艳. 基于对称差分能量算子解调的局部均值分解端点效应抑制方法[J]. 机械工程学报, 2014, 50(13): 80-87.
MENG Zong, LI Shanshan, JI Yan. Restraining method for end effect of local mean decomposition based on energy operator demodulation of symmetrical differencing[J]. Chinese Journal of Mechanical Engineering, 2014, 50(13): 80-87.
[24] 付华, 王婧羽. 基于SR-VMD的微弱故障行波检测方法[J]. 电力系统保护与控制, 2021, 49(1): 156-162.
FU Hua, WANG Jingyu. Weak fault traveling wave detection method based on SR-VMD[J]. Power System Protection and Control, 2021, 49(1): 156-162.
[25] GUNTHER E W. Interharmonics in power systems[C] // 2001 Conference Proceedings on Power Engineering Society Summer Meeting, July 15-19, 2001, Vancouver, BC, Canada: 813-817.
[26] RILLING G, FLANDRIN P. One or two frequencies? The empirical mode decomposition answers[J]. IEEE Transactions on Signal Processing, 2008, 56(1): 85-95.
[27] PHAM V L, WONG K P. Antidistortion method for wavelet transform filter banks and nonstationary power system waveform harmonic analysis[J]. IEEE Proceedings- Generation, Transmission and Distribution, 2002, 148(2): 117-122.
Inter-harmonics detection based on parameter optimization variational mode decomposition
ZHENG Xiaojiao1, WANG Bin1, LI Bujuan1, YU Min2
(1. School of Information Science and Engineering, Wuhan University of Science and Technology, Wuhan 430081, China;2. School of Science, Wuhan University of Science and Technology, Wuhan 430065, China)
Variational mode decomposition (VMD) has been applied in the field of harmonic detection, but the error is large when the decomposition parameteris artificially set. In order to improve the accuracy of VMD in inter-harmonic detection, first,Schmidt orthogonalization theory is used to orthogonalize the components obtained from VMD pre-decomposition in order to avoid modal aliasing. Then the residual energy corresponding to differentvalues is obtained, and the residual energy value minimization method is used to optimize the parameter, and then extract the inter-harmonic signal. Finally, a symmetrical difference energy operator is used to obtain characteristic information such as the amplitude and frequency of the inter-harmonic signal. Simulation results show that the proposed method can effectively optimize the parameterand reduce the VMD decomposition error. Compared with empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD) and synchrosqueezing wavelet transform (SST) proposed in recent years, parameter optimized variational mode decomposition is more effective in inter-harmonic detection and has higher detection accuracy.
inter-harmonic; variational mode decomposition; Schmidt orthogonality; residual energy; symmetric difference energy operator
10.19783/j.cnki.pspc.211054
国家自然科学基金项目资助(51877161);湖北省教育厅科研计划指导项目资助(B2018006)
This work is supported by the National Natural Science Foundation of China (No. 51877161).
2021-08-09;
2021-10-05
郑晓娇(1998—),女,硕士研究生,研究方向为电力系统信号处理与检测;E-mail: 1014226818@qq.com
王 斌(1963—),男,通信作者,教授,博士生导师,研究方向为电力系统运行分析与计算机控制;E-mail: binwang907@163.com
喻 敏(1977—),女,博士,讲师,研究方向为分形理论及其应用。E-mail: yufeng3378@163.com
(编辑 许 威)
