高精度流动单元分类方法及应用

王猛，董宇，张志强，刘志杰，刘海波，周悦

（中海油田服务股份有限公司，河北 廊坊 065201）

0 引言

东海陆架盆地西湖凹陷天然气资源丰富，其主力目的层花港组和平湖组是典型的低孔低渗砂岩储层。在进行储层评价时，对储层进行分级分类综合评价是最有效的方法之一[1]。由于基于数学手段的流动单元划分方法对非常规资料需求少，且定量化程度高[2]，在行业中应用较为广泛。目前常见的分类主要有根据孔喉半径的Winland R35分类[3]以及基于流动单元指数FZI的分类[4]。流动单元通过将具有相似孔隙结构、统一孔渗关系的储层划为同类[5-6]，使得每类储层的孔隙度与渗透率具有良好相关性，因此，基于岩心参数可以建立高精度的渗透率模型。但在非岩心段，则需要根据测井参数计算的流动单元指数划分流动单元，计算误差较大，无法实现储层流动单元的准确划分，进而导致渗透率的计算误差较大[7-8]。

针对传统流动单元划分方法存在的问题，本文提出了一种基于集成神经网络的流动单元分类方法，将流动单元的定量计算转化为定性识别，有效避免了传统方法在流动单元划分时所产生的误差逐级传递[9-10]。

1 研究区地质概况

西湖凹陷是以新生代充填为主的沉积凹陷，是东海陆架盆地具有较大规模和油气勘探开发潜力的构造单元。H气田位于西湖凹陷中央洼陷带，主力含气层为花港组。该层为湖泊-辫状河三角洲体系中的水下分流河道砂体，呈复合体叠置分布。从取心和分析化验资料看，其储层孔隙结构复杂，非均质性强，同一套层系内渗透率相差几个数量级，采用传统孔渗关系建立的渗透率模型对其计算的误差相对较大。

2 基于岩心的流动单元分类

2.1 流动单元指数的意义

对于均匀孔隙介质，Kozeny[11]根据毛细管理论提出了一个渗透率计算公式，其后Carman[12]进行了证明，建立了 Kozeny-Carman公式。 其常用形式[13]为

式中：K 为渗透率，10-3μm2；φ 为有效孔隙度；a为地区经验常数；Sgv为矿物颗粒的比表面积，μm-1。

基于平均水动力单元半径理论，Amaefule等[4]将储层孔喉视为一系列的毛细管，并利用达西定律求解Poisson方程，得出不同流动单元类型下的孔渗关系：

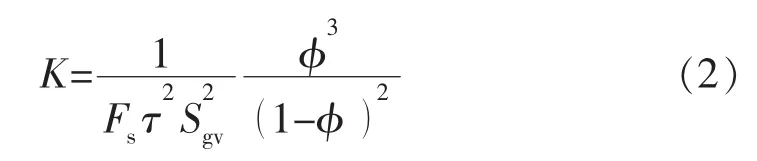
式中：Fs为孔隙几何形状指数（圆柱形管时为2）；τ为流动路径的弯曲度。

在同一流动单元内，式（2）中的Fsτ2为一固定值，但不同流动单元的是变化的[14]，Amaefule 等据此对式（2）变形，定义了流动单元指数：

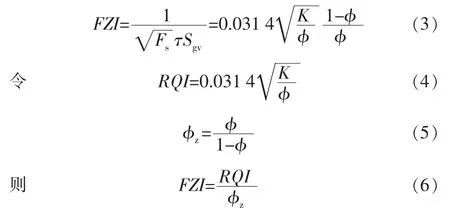
式中：FZI为流动单元指数；RQI为储层品质因子；φz为孔隙度指数。

对式（6）两边取对数，得：

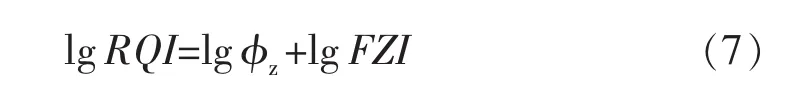
由式（7）可知，同一FZI值样品的RQI与φz的比值相同，在RQI-φz双对数坐标系（见图1）中则表现为在一条直线上。在该直线上及其附近的样品具有相似的孔喉特征，从而构成一个流动单元[14]。当存在多个流动单元时，FZI值整体呈正态分布，因此，在累积概率图（见图2）上则表现为折线[15-17]。

图1 不同流动单元RQI-φz的关系

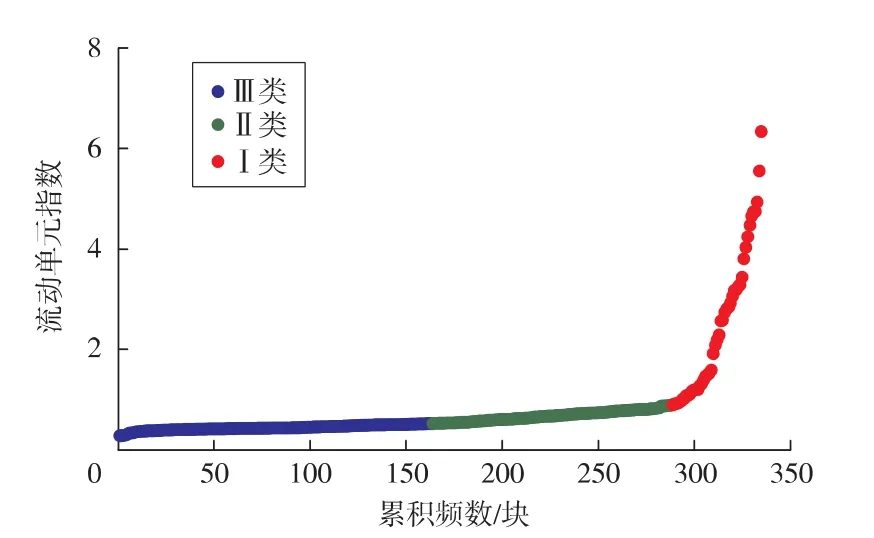
图2 流动单元划分标准

2.2 基于FZI的渗透率模型建立

从西湖凹陷H气田3口井共计取心335块。依据岩心实验分析的孔渗数据计算流动单元指数，其值介于0.27～6.33，平均值为0.81。参照图2可划分各类流动单元的FZI值范围，并依据该划分标准将储层划分为3类流动单元（见图3、表1）。其中，以Ⅱ，Ⅲ类岩心居多。Ⅰ，Ⅱ，Ⅲ类流动单元的孔渗拟合系数分别为0.88，0.87，0.80，相对于传统渗透率计算模型精度大幅度提升，可以满足储层渗透率精细评价的要求。

图3 岩心分类渗透率与孔隙度回归模型

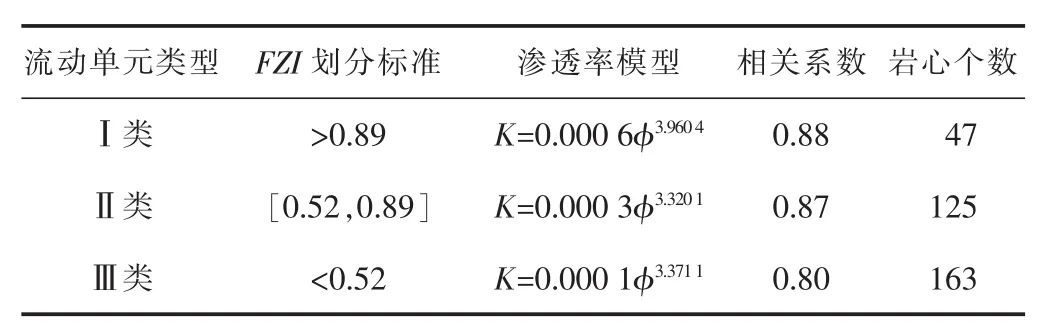
表1 H气田基于流动单元分类的渗透率模型

3 基于测井的流动单元指数计算

在取心段，对岩心物性分析得到的孔隙度、渗透率数据，经过岩心深度匹配后，可根据式（6）、（7）计算FZI，进而对储层进行分类。但在非取心段，仅能根据常规测井数据建立FZI与测井响应之间的关系模型[18]，或建立储层流动单元类型与测井响应之间的关系模型，进而完成储层分类。

3.1 FZI计算模型输入测井参数选择

在建模之前，根据式（6）可完成模型参数的初步筛选。由于τ与地层因素有关[19]，即与电阻率（深侧向电阻率RD、浅侧向电阻率RS、微电阻率RMSL）等测井参数有关，而K，φ（即根据岩心计算得到的孔隙度）可由测井参数自然伽马GR、自然电位SP、校正补偿中子CNCF、密度ZDEN、纵波时差DTC计算得来，同时，常规测井得到的泥质体积分数VSH、孔隙度POR（即通过校正补偿中子-密度交会得到的孔隙度）一般能满足解释精度要求，也可以参与建模；因此，初步选择参与建模的测井参数有 GR，SP，CNCF，ZDEN，DTC，RD，RS，RMSL，POR，VSH10种。初筛完成后，开展参数敏感性分析，选取对FZI最敏感的参数及组合，建立FZI模型。

由于FZI与参与建模的测井参数之间并不是简单的线性关系，因此本文采用更适合刻画非线性相关性的Spearman秩相关系数进行再次筛选。表2为利用岩心孔渗参数计算的FZI与测井参数及其计算参数进行相关系数的计算结果。可以看出，整体上FZI与POR，RMSL，VSH，ZDEN有较高的相关性，因此，最终选取这4种为输入参数，建立FZI计算模型。

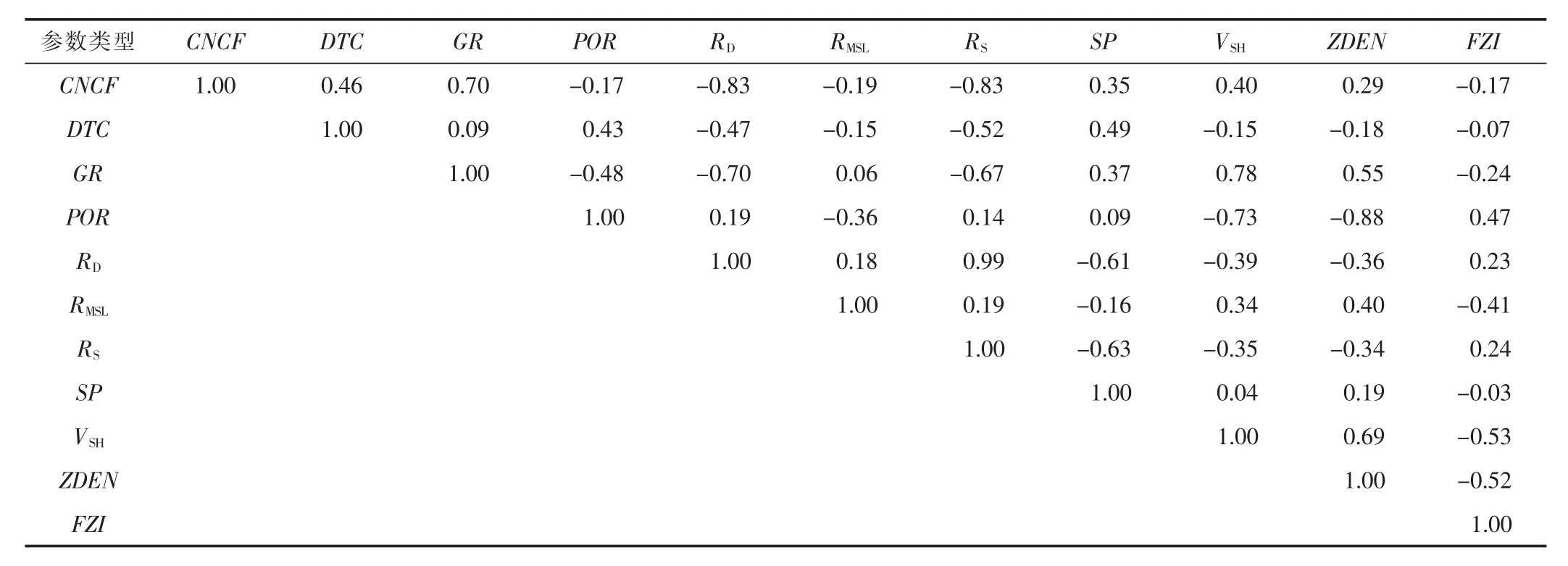
表2 H气田流动单元指数敏感参数Spearman秩相关系数矩阵

3.2 流动单元指数模型建立

剔除缺省测井参数值后的岩心，共计323块，从中随机选取分属3类流动单元的岩心各5块，作为测试集，验证模型分类的准确性；再以其余308块岩心的FZI为因变量，以测井参数 ZDEN，RMSL，POR，VSH为自变量，利用多元回归方法建立FZI计算模型：

利用式（8）计算建模岩心的FZI，与根据岩心孔渗数据计算的FZI对比，平均相对误差为32%，流动单元分类准确率为56%。根据式（8）计算测试集岩心的FZI，与利用岩心孔渗数据计算的FZI对比，平均相对误差为34%，流动单元分类准确率为80%，其中，Ⅰ，Ⅱ，Ⅲ类流动单元分类准确率分别为100%，80%，60%。

建模岩心数量最多的Ⅲ类流动单元判别准确率最低，仅为60%，且建模岩心流动单元类型判别准确率也较低，仅为56%。由此可知，利用多元回归模型的方法并不能准确划分储层流动单元类型。

4 基于集成神经网络的流动单元分类

由于多元回归方法无法满足准确计算流动单元指数的需要，因此引入了基于机器学习算法的流动单元分类方法，以流动单元类型为目标值、测井响应为特征值，训练分类模型包括决策树、Fisher判别[19]等。 上述方法避开了计算FZI环节，直接划分流动单元类型，可有效降低误差传递。

4.1 集成神经网络

神经网络是一种模仿动物大脑结构和功能的数学模型，通过调整网络节点间的连接关系，能够有效拟合输入与输出变量之间的非线性映射关系[20-26]。神经网络中各个运算节点称为神经元，输入、输出相同的神经元构成层，层与层的连接构成了信息的多级传递通道。如图4所示：左侧为输入层，右侧为输出层，中间为若干层状结构的隐藏层，后一层神经元接收前一层所有神经元的输出，经线性运算、非线性激活运算后，再传输到下一层神经元中；多层运算后，神经网络便可拟合输入和输出变量之间复杂的非线性映射关系了。

图4 神经网络示意

在网络模型的训练方面，通常采用反向传播算法（BP），利用链式求导法则，逐层求取每一层神经元损失函数对权重和偏置项的导数，依据各类最优化方法，逐层更新神经元中的权重和偏置项。理想情况下，模型参数沿着梯度降最大的方向进行优化，直至梯度降为0；但梯度为0的点不一定是全局最小点，跳出局部最优陷阱最好的方法就是随机，即随机初始化网络参数和随机梯度下降。

通过训练多个分类器，并将多个分类器组合成一个预测模型，以达到改进预测效果的方法，称为集成学习（Ensemble learning）。同时，集成学习中对数据集进行有放回抽样、构建多个小样本集、训练多个模型的策略，也有利于改善样本类型不均衡和样本过少的影响。通过随机模型参数和随机抽样训练样本的方法，可以得到多个独立的分类器，然后通过投票显著降低模型误差。

4.2 网络模型训练

本文实验井岩心样本数据共计335块，同样剔除缺省测井参数值的样本，其余可用样本集为323块。从样本集中随机抽取分属每类流动单元的各5块样本作为测试集，剩下的308块作为训练集。训练集中Ⅰ类流动单元样本仅有32块，Ⅲ类流动单元却多达158块，样本类型极度不平衡。过采样前测试集的预测结果偏向Ⅱ，Ⅲ类，运用SMOTE算法过采样后模型过拟合，测试集的预测结果依旧偏向Ⅱ，Ⅲ类，因此，需要寻求新的数据处理方法。

集成学习是通过构建并集成多个学习器以生成一个稳定且在各方面表现都较好的模型。为避免不平衡数据以及过采样数据对训练结果的影响，本文采用下采样的方法，即将数据集分割成若干个数据平衡的子训练集，利用子训练集训练若干个神经网络分类器进行组合。

由于神经网络本身可以提取特征，因此不必进行特征选取。将流动单元类型从Ⅰ类到Ⅲ类序号编码为[0，1，2]，这样，转换后依然会保留类型优劣关系。 此外，为了避免梯度消失现象，优化网络训练效率，还需要对训练集和测试集的特征进行归一化处理。

经多次测试，本文采用3层隐藏层结构，从前至后神经元个数依次为[20，10，5]，第1隐藏层用于特征提取，第2、第3隐藏层用于特征精练。随机初始化模型参数，利用分割好的若干子训练集训练1 000个神经网络模型，然后通过投票的方式预测流动单元类型。最终训练集的预测结果分类准确率为93%，测试集的预测结果分类准确率为93%，其中，Ⅰ，Ⅱ，Ⅲ类流动单元分类准确率分别为100%，80%，100%。

对比2种流动单元分类方法可以看出，集成神经网络模型在训练集的分类准确率较多元回归分类提高了37%，在测试集的分类较多元回归分类准确率提高了13%。——表明集成神经网络在流动单元分类上具有优越性。

5 应用分析

西湖凹陷H气田岩心实验分析孔隙度分布在2%～20%，平均孔隙度为8.9%；岩心实验分析渗透率分布在 0.016×10-3～244.000×10-3μm2， 平均渗透率为4.050×10-3μm2。根据335块岩心资料的分析统计结果，将西湖凹陷花港组储层分为3类（见表1），并按类型建立岩心孔渗模型。为解决测井参数计算FZI误差大及各类数据分布不均的问题，将训练集划分为多个数据平衡的子训练集，用于训练集成神经网络。根据神经网络模型在全井段划分纵向流动单元类型，再根据表1中不同类型流动单元的渗透率模型计算全井段渗透率，H气田部分井段渗透率精细处理结果见图5。

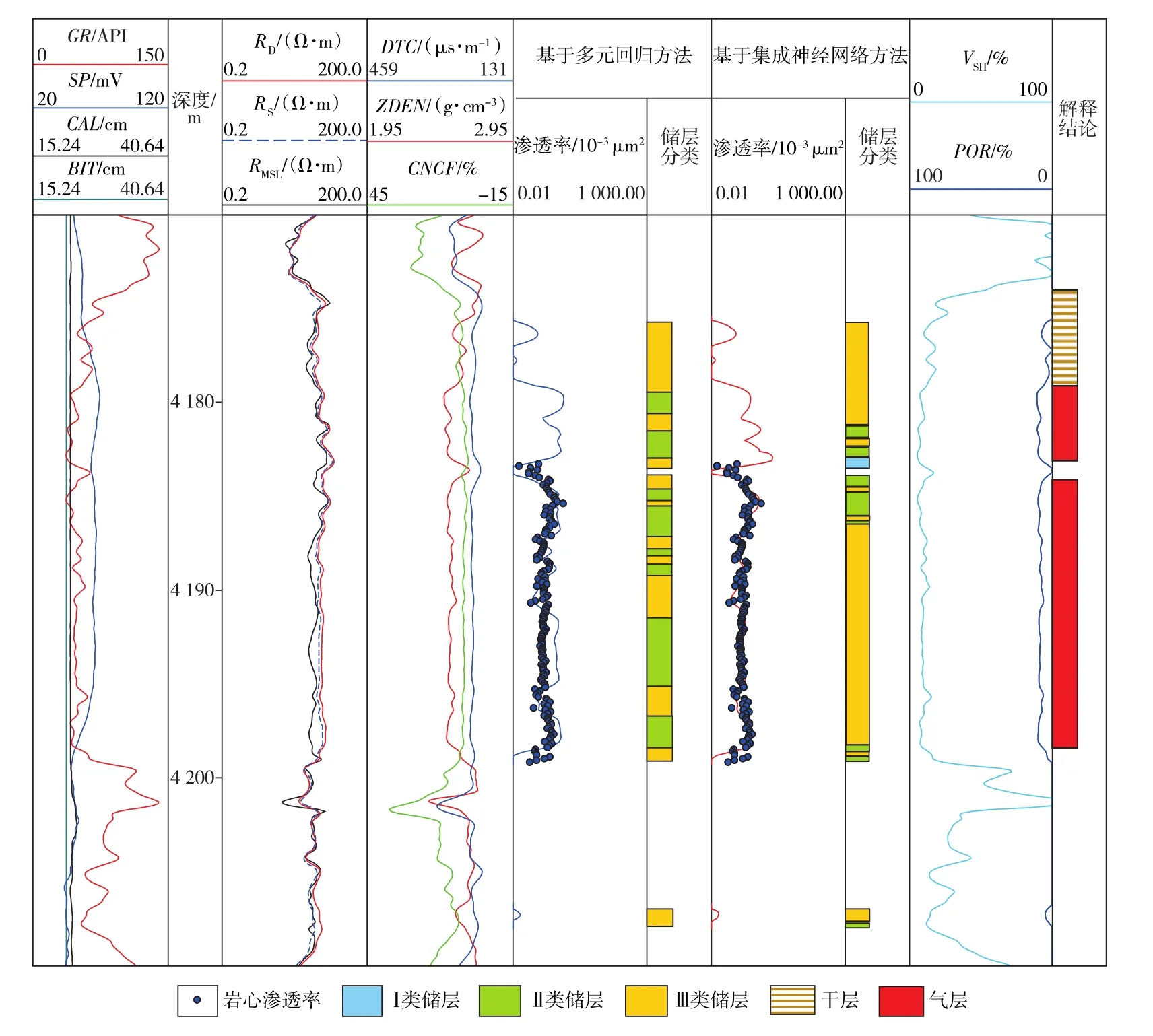
图5 H气田部分井段测井资料处理与解释成果

图5中第6列为基于多元回归方法计算的FZI，再依表1分类标准所得的储层流动单元类型；第5列为根据第6列储层流动单元分类计算得到的渗透率，与岩心实验分析渗透率相比，二者平均相对误差为115%。第8列为基于集成神经网络模型直接分类所得储层流动单元类型；第7列为根据第8列储层流动单元分类计算得到的渗透率，与岩心实验分析渗透率相比，二者平均相对误差为38%。由图5可知：第5列中的计算渗透率与岩心实验分析渗透率误差较大的层段，为误判的储层流动单元类型层段，采用集成神经网络算法的储层流动单元分类误判较少；因此，第7列中的计算渗透率与岩心实验分析渗透率的误差要远小于第5列。

6 结论

1）基于流动单元分类建立的渗透率模型具有较高的计算精度；但在模型应用阶段，由于根据测井参数计算的流动单元指数误差较大，使得储层流动单元无法准确分类。

2）基于机器学习算法的流动单元分类方法，利用测井参数直接划分储层流动单元类型，可有效降低误差传递，但各类流动单元中岩心分布不均衡，会导致模型分类结果偏向于岩心较多的类；因此，常规的神经网络模型无法适用。

3）本文基于集成神经网络的流动单元分类方法，将数据集分割成若干类型平衡的子训练集，利用子训练集训练若干参数随机初始化的神经网络模型，可使网络模型跳出局部最优陷阱，同时可降低数据类型不均衡对预测结果的影响。

4）实际应用表明，本文方法划分储层流动单元类型的准确性较多元回归方法高，据此计算的储层渗透率与岩心实验分析渗透率吻合度高，与多元回归方法相比，误差降低了77%，推广应用前景良好。