基于GA-KELM的ZPW-2000A型轨道电路故障预测研究
2022-06-11李晓艳
李晓艳
(陕西铁路工程职业技术学院 铁道动力学院,陕西 渭南 714000)
伴随着设计时速350 km,正线全长174 km的京张高铁“精品工程、智能高铁”的建设,铁路线路针对轨道电路所采用的“天窗修(TBM)”和“故障修”的维修维护模式[1-2]已不能满足行车安全和运输效率的提高.
当前已有不少文献对轨道电路进行了深入研究:文献[3]就轨道电路锈蚀、集污造成轨面电阻超高导致分路不良进行研究;文献[4]就轨道电路检测精度低、耗时长等方面进行算法改进;文献[5]针对轨道电路中红光带故障的多样性及复杂性问题进行故障诊断;文献[6-10]中对道砟信号、多故障诊断方法等方面进行了研究.
随着智能技术及PHM(Prognosticsand Health Management,故障预测与健康管理)理论的发展,基于状态修(CBM)的故障预测方法成为当前的研究热点[11-12].典型故障预测的方法主要有:统计法、数学法、智能法和传统基于梯度的学习迭代策略,选择正则化最小二乘法调整输出矩阵,在网络训练速度及泛化速度方面都有很大的改善[14].本文选择ELM及其优化算法对我国铁路线路上广泛采用的ZPW-2000A型轨道电路进行故障预测研究,最后通过两个实例验证了模型的可行性与有效性.
1 ZPW-2000A结构分析
图1为ZPW-2000A型轨道电路的结构图.室外由调谐区、机械绝缘节、匹配变压器、补偿电容、电缆和调谐区引线构成.室内主要有发送设备和接收设备组成.
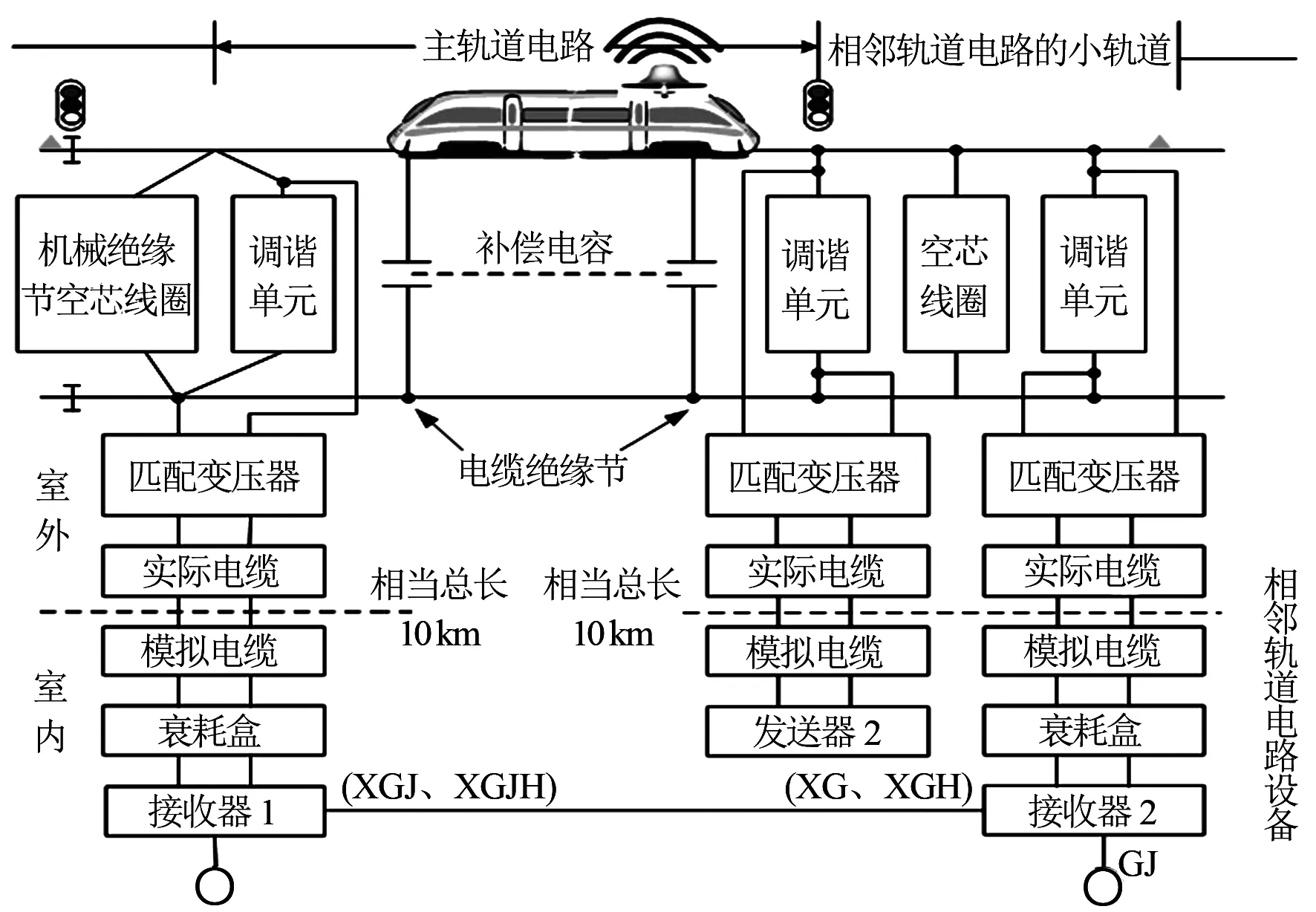
图1 ZPW-2000A型频轨道电路原理图
本文数据来自微机检测室,具体参数指标如表1所示.
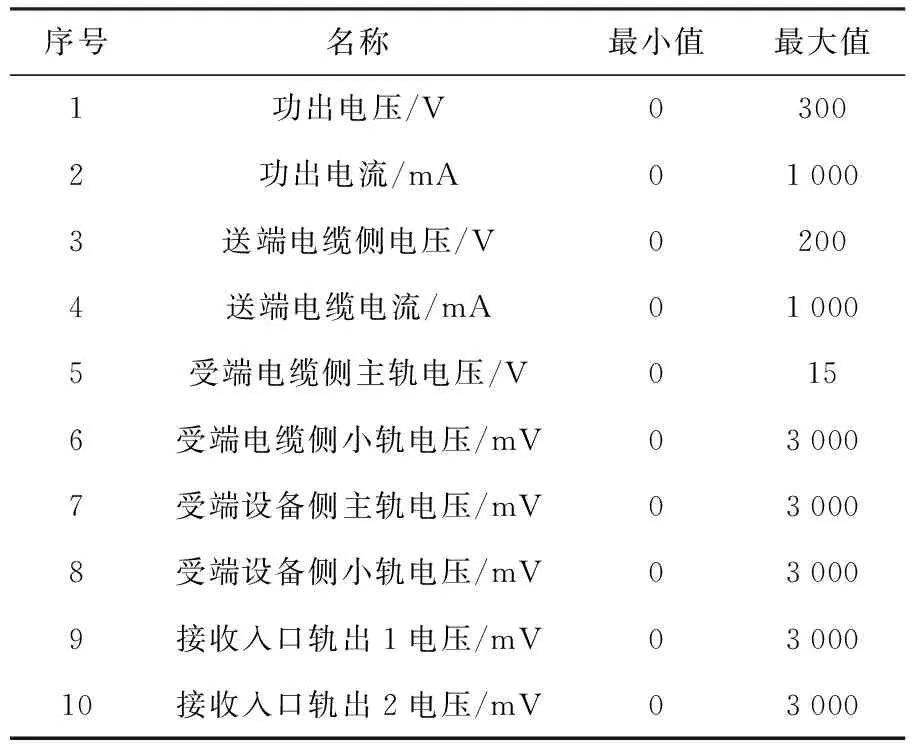
表1 轨道电路集中监测基本数据
2 ELM及其改进算法
ELM是一种单隐层前馈神经网络,包括输入、隐层和输出3层.若有N组训练样本数据集(xj,tj),(xj,tj)∈Rn×Rm,隐含层节点数L,激励函数v,则:
(1)
其中,j=1,…,N,βi为第i个隐层节点和输出层节点间的权重向量.
ELM随机选择隐层节点的输入权重w和偏置b,再计算出权重β的最小二乘解,保证训练错误率最小.式(1)可被重新写为:
Hβ=T
(2)
则有:
其中,H为隐层节点输出,其特征映射为:
h(xj)=[v(w1xj+b1), …,v(wLxj+bL)]
其中,β为输出权重矩阵,T为目标矩阵.
在训练数据集中ELM训练过程包含3步,即:
Step1:随机产生输入权重wi与偏置bi,1≤i≤L; Step2:求取隐层的输出矩阵H;
Step3:计算输出权重矩阵β=H+T.
其中,H+为隐层输出矩阵H的Moore-Penrose广义逆.当HHT为非奇异时,H+=HT(HHT)-1.为消除“病态矩阵”造成的误差引入正则化系数η,网络的输出权重最小二乘解可表述为:
β=HT(HHT+ηI)-1T
(3)
则ELM相应输出矩阵为:
y(x)=h(x)β
(4)
将核函数引入到ELM中,形成新的核函数KELM.
KELM重新定义核函数QELM=HHT,其元素为:
QELM(i,j)=h(xi)h(xj)=K(xi,xj)
(5)
网络输出表示为:
(6)
核函数K(xi,xj)的类型确定为径向基核函数,即:
(7)
其中,γ为径向基核函数的核参数.
2.1 O-KELM方法及其算法
核极限学习机的优化过程主要在于确定正则化系数η与径向基核参数γ.在O-KELM过程中适应度评价函数越小,网络性能越好,则均方误差值ERMSE(y*,y)可表述为:
(8)
其中,y*(i)为方法的预测输出,y(i)为实际输出.
待优化的决策变量由γ与η共同组成,形成种群个体,即ah=[γ,η],h=1,2,…,m,其中m表示种群个体数目.变量归一化过程可表述为:
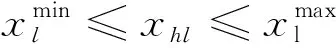
(9)
Step2:为方便计算个体评价函数,将个体的决策量转化到真实范围.
2.2 GA-KELM算法
选择遗传(GA)、微分(DE)与模拟退火(SA)3种算法对ELM的核参数γ、正则化系数η进行优化.再分别与典型算法:SVM、ELM、KELM在应用对象预测中进行等条件比对.
GA主要累积的信息在可行域中进行,具体GA-KELM的实现如下.
Step1:初始化种群A:
A=[a1,…,am]
(10)
Ah=[ah1,…,ahl]T
(11)
其中,0≤ahl≤1,h=1,2,…,m,m代表种群容量,l为待优化决策的数目.
Step2:根据式(8)计算个体的适应度.
Step3:由算法结合个体适应度值选择双亲,再以概率pc进行均匀交叉操作产生新一代种群.
Step4:以概率pm进行均匀变异操作.
3 预测结果验证方式
O-KELM模型中的时间序列表述如式(12),式中D为预测步长,Δ为嵌入维数;xt包括历史数据(yt-1,yt-2,…,yt-Δ)因素.
y(t+D)=f(xt),∀t=Δ,…,l
(12)
选择平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方误差(NMSE)和相对误差百分比(REP)作为预测结果的评价指标,具体如式(13)~式(16)所示.
(13)
(14)
(15)
(16)
其中:y(i)为时间序列对应的实际输出;y*(i)为相应模型预测输出;N为预测样本点数;δ2为待预测时间序列方差.
4 模型高效性验证
选择某区段2016年1月-2018年1月ZPW-2000A数据台账中轨出1和轨出2的电压值进行改进算法样本值的训练.通过预测2018年2月(28天)的输出结果,对各算法的预测性能进行评判,具体数据如下:区段名称:1 128 G;载频2 300 Hz;发送电源24.7 V;接收电源25.8 V;功出电压154 V;主轨入电压997 mV;小轨入电压115 mV;轨出1电压656 mV;轨出2电压147 mV.
在算法优化中,ELM模型的隐层节点设置为L=200,选择Sigimoid激活函数,设定核参数初始值γ∈(0.1,300],正则化系数η∈[0,100].KELM核参数γ为6,η=0.01.GA-KELM初始种群选择为150,最大进化代数为300.GA的交叉概率Pc=0.4,变异概率Pm=0.1.训练后的不同算法性能如表2.
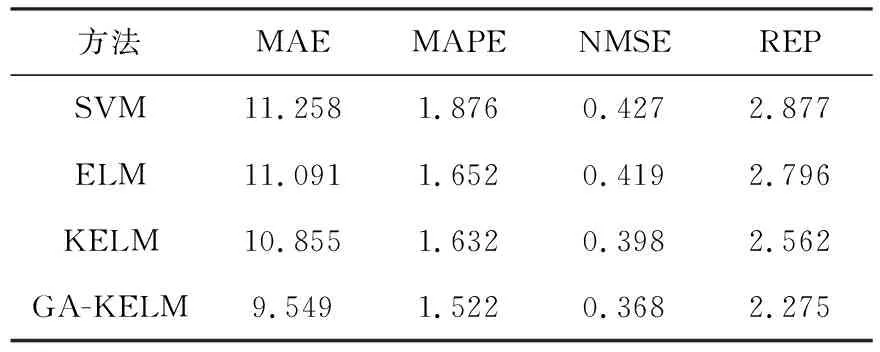
表2 不同方法性能比较
通过给出的SVM、ELM、KELM和GA-KELM算法在2018年2月份的轨出1的数据预测图(图2),得出GA-KELM预测效果最优.
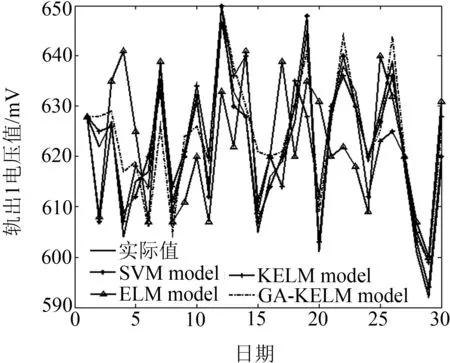
图2 不同预测算法结果对比
5 实例分析
5.1 断轨故障预测
理论上ZPW-200A主轨道的轨出1电压应不小于落下门限(大于等于170 mV);小轨道轨出2电压不低于10 mV,实验数据见表3.针对某局2018年10月某段发生的ZPW-2000A断轨故障,采用GA-KELM算法对其电压趋势进行预测验证.

表3 实验验证数据
图3说明在2018年10月份轨出1和轨出2电压值均低于门限值,验证该优化模型具有一定有效性,便于现场工作人员及时维护保养.
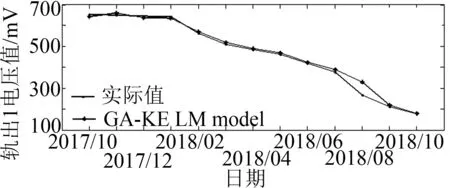
(a)轨出1
5.2 红光带故障预测
本例选自2016年2月15日10∶13∶11-10∶13∶42,京九下行线21793G在空闲状态时出现红光带.21793G属京九线复线自动闭塞区段的一个中继站,该站区间全部采用ZPW-2000A无绝缘轨道电路.如图1中电气绝缘节由调谐单元、匹配变压器、空芯线圈和29 m钢轨组成,实现邻轨道电路间的电气隔离.21793G轨道电路区段全长1 335 m,载频为1 700 Hz.图4列出了某站21793G设备布置图.
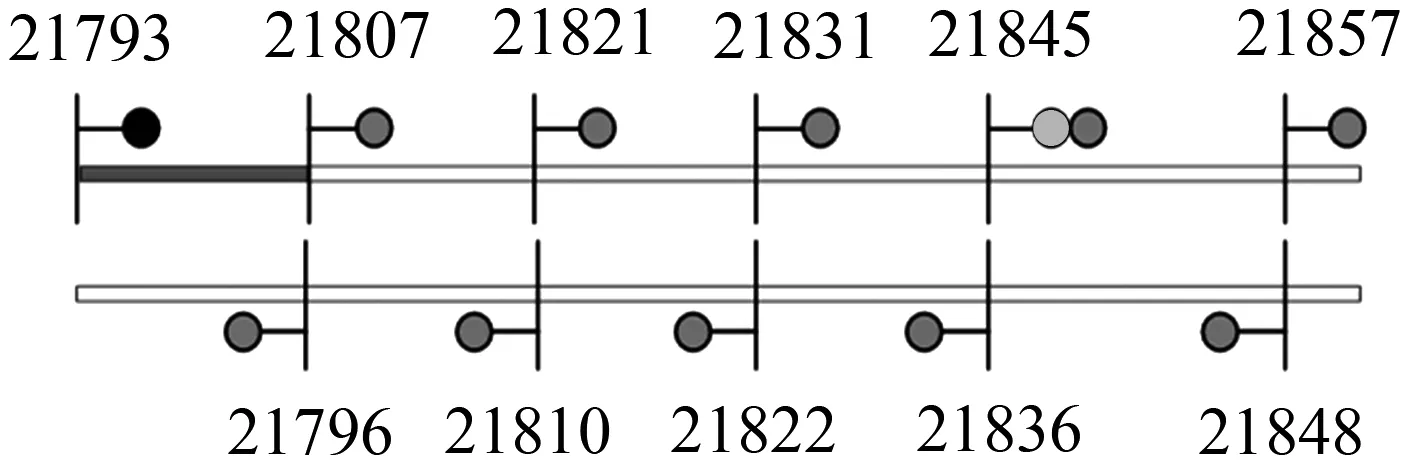
图4 某站21793G设备布置图
通过调阅数据发现:故障处理人员通过CTC设备回放确认21793G在10∶13∶11-10∶13∶42出红光带31 s,微机监测数据显示:
(1)10∶13∶11主轨电压由540 mv突变为0 mv(正常为540 mV),一直持续31 s;
(2)21793G运行前方相邻区段轨道电路电压为0 mV;
(3) 21793G区段移频电缆侧电压突然为134.6 V(正常为61.6 V);
(4) 21793G移频电缆侧接收电压0 mV;
(5) 21793G区段的发送端匹配变压器电缆侧短路146.5 V、电缆侧开路134.7 V、钢轨侧开路32.7 V.
如图5为系统CSM实时输出的监测曲线,本文引入GA-KELM模型与CSM数据结合,通过监测当前时刻主轨道和小轨道两个最敏感特征量参数变化来对设备运行状态进行分析.
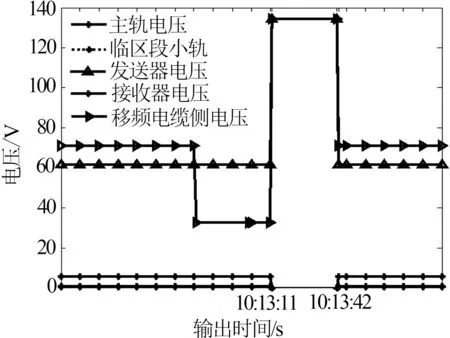
图5 CSM系统输出
如图6,GA-KELM算法的输出结果显示在10∶13左右,主轨出现轨点,主轨轨出电压迅速降为0,预测模型与实际运行情况一致.
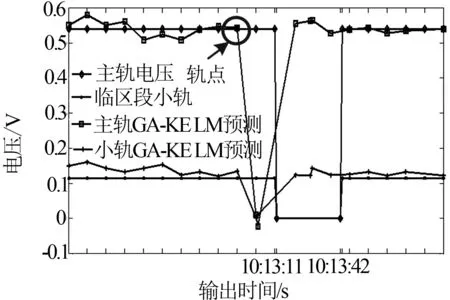
图6 实际输出与优化算法输出比对
通过指导现场人工检修,最终发现是由于送电端匹配变压器钢轨侧开路所致.经测试发现:匹配变压器内部电解电容C1、C2性能不达标,导致匹配变压器钢轨侧开路所致.更换发送端匹配变压器后,793G设备电压恢复正常,通过预测算法快速找到故障点位置并验证了模型的有效性.
6 结论
(1)本文主要针对传统铁路线路中轨道电路维修维护中存在维修不足和维修过剩的问题,建立了一种基于GA-KELM算法的ZPW-2000A型轨道电路的故障预测模型;
(2)通过实例将改进模型性能与传统的SVM、ELM、KELM算法作比对,验证了改进的GA-KELM性能最优;
(3)选择GA-KELM算法对两个实例进行预测分析,验证了模型的高效性.
本文方法对铁路信号设备从定时修、故障修和转向状态修的发展过程具有积极意义.
致谢:本文受陕西铁路工程职业技术学院科技计划基金项目(2014-17)资助,特此致谢!
