改进哈里斯鹰算法及其在FIR滤波器中的应用
2022-06-11郭佳宁杨婧刘婷
郭佳宁 杨婧 刘婷


摘 要:针对原始哈里斯鹰算法(Harris Hawks Optimization, HHO)存在收敛精度低、易陷入局部最优等问题,提出一种改进的哈里斯鹰算法。首先引入Logistic混沌映射加强扰动,丰富种群多样性,提高算法收敛精度;其次用非线性逃逸能量因子代替线性逃逸能量因子,易于跳出局部最优。为了验证改进效果,利用改进算法求解FIR滤波器设计问题。仿真结果表明,与原始哈里斯鹰算法相比,基于改进算法的FIR滤波器具有更加理想的通带和阻带性能。
关键词:FIR滤波器;哈里斯鹰算法;Logistic混沌映射;非线性逃逸能量因子
中图分类号:TP311 文献标识码:A
Improved Harris Hawks Optimization and Its Application in FIR Filter
GUO Jianing, YANG Jing, LIU Ting
Abstract: Aiming at the problems of the original Harris Hawks Optimization (HHO), such as low convergence accuracy and easy to fall into local optimum, this paper proposes an improved HHO. Firstly, Logistic chaos mapping is introduced to strengthen the disturbance, enrich population diversity, and improve the convergence accuracy of the algorithm. Secondly, the nonlinear escape energy factor is used to replace the linear escape energy factor, which is easy to jump out of the local optimum. In order to verify the improvement effect, the improved algorithm is used to solve the FIR filter design problem. Simulation results show that compared with the original HHO, the FIR filter based on the improved algorithm has more ideal passband and stopband performance.
Keywords: FIR filter; Harris Hawks Optimization; Logistic chaos mapping; nonlinear escape energy factor
1 引言(Introduction)
作为数字信号处理的基本技术,有限脉冲响应(Finite Impulse Response, FIR)滤波器在图像、音频、模式识别等方面得到了广泛应用。随着社会的进步与现代生活水平的日益提高,人们对其性能提出了更高层次的要求。一些学者提出基于优化算法来对FIR滤波器进行设计。2018 年,刘飞等[1]提出根据TD-SCDMA的FIR滤波器指标,通过遗传算法求解函数模型,再运用加权最小二乘方法设计滤波器;2019 年,季丹[2]提出将人工蜂群算法应用于FIR滤波器设计;2020 年,陈忠云等[3]提出用改进的疯狂蝙蝠算法(CBA)来设计低通有限脉冲响应滤波器;2021 年,ZHU等[4]提出一种用于相干接收机色散补偿的FIR滤波器。
哈里斯鹰算法是由HEIDARI等[5]提出的一种新型仿生智能优化算法。它模拟老鹰的捕食行为,结合Levy飞行,实现对复杂多维问题求解。它具有参数简单、全局搜索能力强、容易实现等优点,但和其他优化算法一样,在求解复杂问题时,存在收敛精度高、易陷入局部最优等缺陷。
本文的工作如下:
(1)提出一種改进哈里斯鹰算法。首先,利用Logistic混沌映射[6]对种群进行初始化,增强种群多样性;然后用非线性逃逸能量因子[7]替换原本的逃逸能量因子,平衡全局与局部搜索策略,帮助跳出局部最优。
(2)利用改进哈里斯鹰算法对FIR滤波器进行设计,将性能问题转为参数优化问题,根据最小均方误差准则优化滤波器系数。
(3)利用MATLAB软件,对基于改进哈里斯鹰优化算法的FIR滤波器进行仿真,结果表明,经过改进哈里斯鹰算法优化后,FIR滤波器增大了阻带衰减程度,减小了通带范围内波动。
2 哈里斯鹰算法(Harris Hawks Optimization)
哈里斯鹰算法主要分为三个阶段:搜索阶段、搜索与开发的转换阶段、开发阶段。这三种阶段的差异由逃逸能量因子来决定。
(1)搜索阶段
此阶段中猎物体力充沛,老鹰距离猎物较远。此时哈里斯鹰会选择栖息在某个地方,并通过两种策略来更新自身位置以找到猎物。
(1)
式中,表示下一时刻哈里斯鹰的位置,表示当前鹰的位置,表示猎物的位置向量,表示随机选择的猎物位置。是之间的随机数,和是搜索空间的上下限。当时,可以认为没有发现猎物位置,鹰将随机选择种群中的个体,并根据其位置来更新种群位置;当时,表示发现猎物位置,鹰将根据猎物当前位置来更新种群位置。
(2)搜索与开发的转换阶段
全局搜索和不同开发行为之间转化是通过逃逸能量来决定的。逃逸能量定义为:
(2)
式中,为猎物初始能量,;为迭代次数,为最大迭代次数。时进入搜索阶段,反之进入开发阶段。
(3)开发阶段
根据逃逸能量和随机数来决定围捕猎物所用到的策略。
①软包围
时,表示猎物能量充沛,但没有办法跳出包围圈。此时,采用软包围形式,鹰的位置更新为:
(3)
式中,,是[0,2]之间的隨机数,模拟猎物的移动强度。
②渐进式快速俯冲软包围
时,表示猎物能量充沛,且跳出包围圈成功逃脱。此时需要结合Levy飞行来更新猎物位置。
(4)
式中,;,是Levy飞行[8]表达式;和分别是求解Levy飞行所需的维数和随机向量。
③硬包围
时,表示猎物能量不足,且没有办法跳出包围圈,因此采用硬包围。此时位置更新为:
(5)
④渐进式快速俯冲硬包围
时,表示猎物能量不足,但能够跳出包围圈,因此采用渐进式快速俯冲硬包围,此时位置更新为:
(6)
式中,;。
3 改进哈里斯鹰算法(Improved Harris Hawks Optimization)
(1)Logistic混沌映射
“混沌”一词来源于非线性动力系统,这一过程具有确定性、遍历性、收敛性和对初值极其敏感的特性,多被用于初始化种群。本文提出Logistic混沌映射用来调整初始种群,公式如下:
(7)
式中,表示当前鹰的位置,是随机数。经实验证明,的最优值为4,故此处令。
(2)非线性逃逸能量策略
在原始哈里斯鹰算法中,利用逃逸能量来决定搜索和开发之间的转换,但由于逃能量是线性减少,迭代次数累加后只能用于进行局部搜索,容易陷入局部最优。因此,提出一种非线性逃离能量因子来代替原来的线性计算逃逸能量,平衡全局与局部搜索策略,帮助跳出局部最优。其公式如下:
(8)
式中,为最大迭代次数,表示更新的逃逸能量。
由于逃逸能量因子在猎物体力充沛()时对最优值的结果影响较大,因此,在软包围和渐进式快速俯冲软包围两种策略时删除了能量因子,使寻优结果变好。
4 改进算法设计FIR滤波器(FIR filter design based on improved algorithm)
传统FIR滤波器的设计方法包括窗函数设计法和频率采样法。尽管这些方法简单,容易实现,但由于计算机要求参数必须是有限字长,就会产生截断,使得实际滤波与理想滤波相差过大,因此应用改进哈里斯鹰算法对离散参数中的滤波器系数进行优化设计,使得滤波器的性能得以提高。
设阶FIR的单位冲激响应为,经过z变换以后的函数为:
(9)
令,得出h(n)的频率响应为:
(10)
在滤波器优化设计之前首先要确定最优化准则,FIR滤波器中有两种优化准则:均方误差最小化准则和最大误差最小化准则。本文选择均方误差最小化准则,假如FIR滤波器的理想幅频响应为,实际的滤波器幅频响应为,则理想滤波器和实际滤波器在样点上的两个幅频响应和的误差平方和为:
(11)
将式(10)代入式(11)可得式(12):
(12)
根据均方误差最小化准则得出,当E最小时,对应的滤波器系数就是所找到的最优值。由式(12)可以看出,的最优问题是优化问题,所以能够用改进后的哈里斯鹰算法求解上述问题。本文将式(12)作为适应度函数来设计FIR滤波器,即:
(13)
由式(13)可知,越小,滤波器系数越小,对应的滤波器性能越好。
改进哈里斯鹰算法的实现步骤如下:
步骤 1:初始化种群。根据搜索空间的上下界和,并利用式(7)初始化种群内个体。
步骤 2:计算初始适应度值。根据式(13)计算种群的适应度值,将适应度值最优的个体位置设为当前猎物位置。
步骤 3:位置更新。在这一阶段提出四种围捕猎物的策略,并对应四种不同的哈里斯鹰位置更新方式。用式(8)计算逃逸能量,并生成随机数,若则鹰进行软包围;若则鹰进行渐进式快速俯冲软包围;若则鹰进行硬包围;若则鹰进行渐进式快速俯冲硬包围。
步骤 4:重新计算适应度。重新根据式(13)计算更新位置后的适应度值并与初始适应度值进行比较,如果优于初始值,则将更优适应度值对应的个体位置作为当前种群位置,反之适应度值不变。
步骤 5:重复步骤 3 和步骤 4,判断迭代次数是否达到,如果达到,输出当前位置,此时最优解即为滤波器的系数;如果没有达到,则返回继续进入循环。
5 仿真结果(Simulation results)
为了验证本文算法改进的有效性,利用MATLAB软件对基于改进算法的FIR滤波器进行仿真,并与用原始哈里斯鹰算法设计的滤波器进行对比。在仿真实验中,算法的参数设置为:种群大小,最大迭代次数。
例1:设计一个阶数为N=20的低通滤波器,其技术指标为:
(14)
例2:设计一个阶数为N=20的高通滤波器,其技术指标为:
(15)
例3:设计一个阶数为N=20的带通滤波器,其技术指标为:
(16)
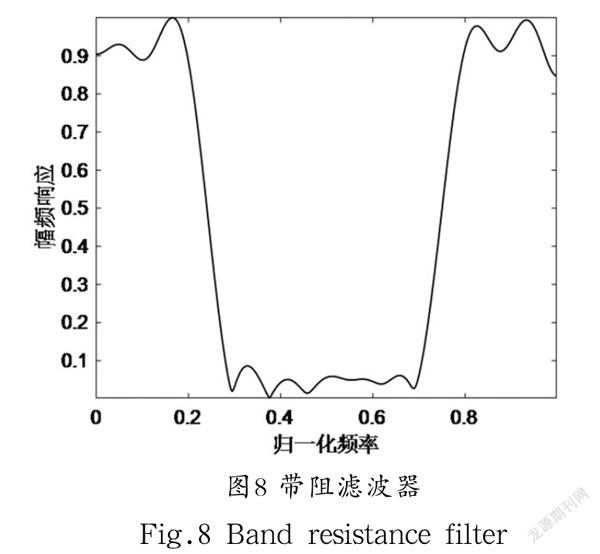
例4:设计一个阶数为N=20的带阻滤波器,其技术指标为:
(17)
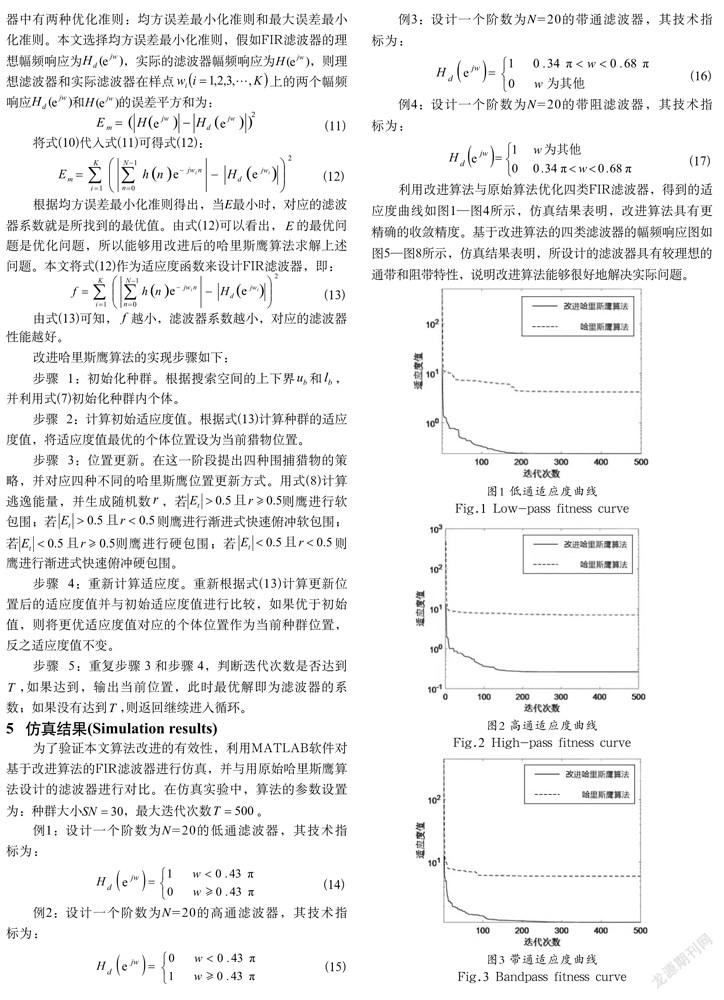
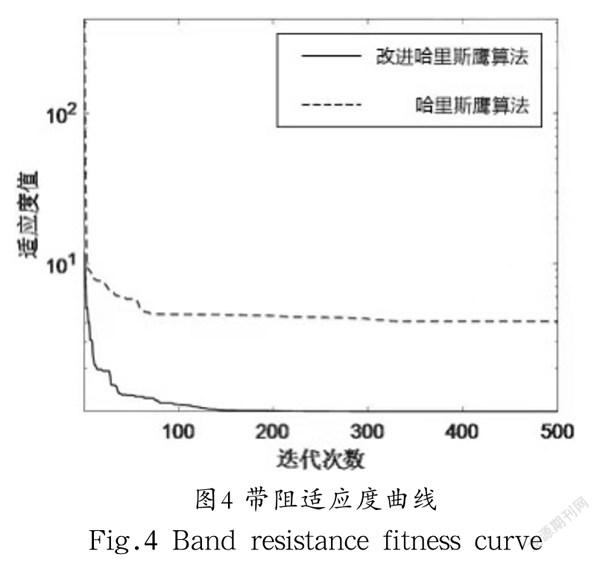
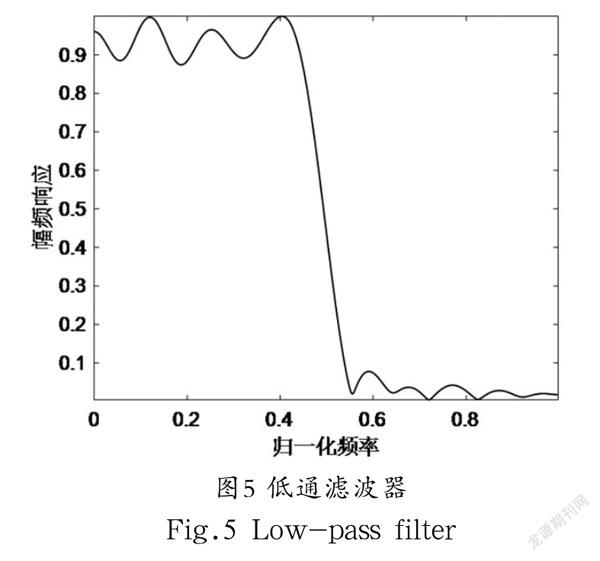
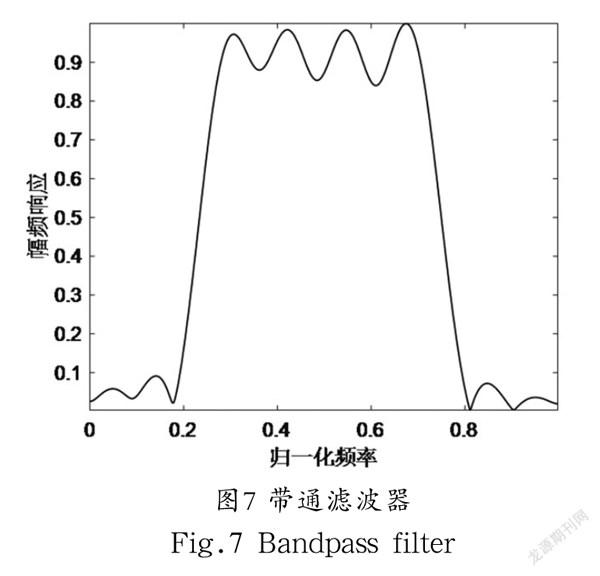
利用改进算法与原始算法优化四类FIR滤波器,得到的适应度曲线如图1—图4所示,仿真结果表明,改进算法具有更精确的收敛精度。基于改进算法的四类滤波器的幅频响应图如图5—图8所示,仿真结果表明,所设计的滤波器具有较理想的通带和阻带特性,说明改进算法能够很好地解决实际问题。
6 结论(Conclusion)
为了解决原始哈里斯鹰算法中收敛精度低、易陷入局部最优等问题,本文提出一种改进的哈里斯鹰算法。为了验证改进效果,利用改进算法求解FIR滤波器设计问题。仿真结果表明,与原始算法相比,基于改进算法的FIR滤波器减小了通带波动,增大了阻带衰减程度,滤波器性能更优,证明了该方法的有效性。
参考文献(References)
[1] 刘飞,丁岩,郭霞霞,等.遗传算法在FIR滤波器设计中的应用[C]//浙江省信号处理学会.浙江省信号处理学会2018年学术年会论文集.科学技术协会,2018:89-99.
[2] 季丹.人工蜂群算法在FIR濾波器设计中的应用研究[J].信息记录材料,2019,20(01):51-53.
[3] 陈忠云,张达敏,辛梓芸,等.疯狂蝙蝠算法的低通FIR滤波器设计[J].计算机应用研究,2020,37(07):2058-2062.
[4] ZHU X F, LU Y, LI C Q, et al. Design of dispersion compensated FIR filter for coherent receiver[J]. Chinese Journal of Quantum Electronics, 2021, 38(01):17-24.
[5] HEIDARI A A, MIRJALILI S, FARIS H, et al. Hariis hawks optimization: Algorithm and applications[J]. Future Generation Computer Systems, 2019(97):849-872.
[6] 韦丞婧,李国东.基于超混沌系统和Logistic映射的视频图像加密设计[J/OL].计算机工程.(2021-08-24)[2022-03-22].https://kns.cnki.net/kcms/detail/detail.aspx?DOI=10.19678/j.issn.1000-3428.0061608.
[7] ZHANG Y, ZHOU X Z, SHIH P C. Modified Harris hawks optimization algorithm for global optimization problems[J]. Arabian Journal for Science and Engineering, 2020, 45(12):10949-10974.
[8] 梁田,曹德欣.基于莱维飞行的改进简化粒子群算法[J].计算机工程与应用,2021,57(20):188-196.
作者简介:
郭佳宁(2001-),女,本科生.研究领域:智能信号与信息处理.
杨 婧(2000-),女,本科生.研究领域:智能信号与信息处理.
刘 婷(1981-),女,博士,副教授.研究领域:智能信号与信息处理.
