基于跳跃、好坏波动率的混频已实现EGARCH模型的波动率预测与风险度量
2022-06-10郭宝才
郭宝才,项 琳
(1.浙江工商大学 统计与数学学院,浙江 杭州 310018;2.浙江工商大学 统计数据工程技术与应用协同创新中心,浙江 杭州 310018)
一、 引 言
在金融资本市场中,投资组合优化、风险管理和衍生品定价等金融应用的准确实施依赖于对资产收益波动的准确建模与预测。因此,有关波动率建模的研究一直是金融计量经济学中最活跃的领域之一。其中,最常见的是GARCH族模型,此类模型能够很好地刻画资产收益率的异方差性和波动聚集性。然而,GARCH族模型通常使用同一频率的数据,未能充分利用蕴含丰富波动信息的日内高频数据与周、月等长期数据,因此无法在时间尺度上更精细地刻画波动率,也并不适用于研究金融市场波动的长期驱动因素[1]。
金融市场及计算机技术的高度发达使得金融资产的高频交易普遍存在,资产价格受各方因素的影响迅速变化,这给波动率的研究带来了新的机遇与挑战。随着高频金融数据获取难度的降低,学者们构建了众多包含日内高频收益信息的已实现测度(Realized Measure),其中应用最为广泛的是由Andersen和Bollerslev(1998)[2]提出的已实现波动率(Realized Volatility,RV)。已实现测度作为真实积分波动率(Integrated Volatility,IV)的估计,具有计算简便、稳健性等多重优势。为在GARCH模型的框架下引入包含高频信息的已实现波动率,Engle(2002)[3]将其直接作为外生变量加入波动方程中,以此构造GARCH-X模型,但该模型不能合理解释已实现波动率的变动。为解决这一问题,Hansen等(2012)[4]引入测量方程提出Realized GARCH模型,并由Hansen和Huang(2016)[5]将模型拓展为结构更加灵活的Realized EGARCH模型,实现了对日收益率和包含日内高频信息的已实现波动率的联合建模,在实证中取得较优的拟合与预测效果。此后,学者们[6-9]不断研究并拓展Realized GARCH模型,并将其广泛应用于金融市场的实证研究中。以上研究显示,日内高频价格信息对于GARCH族模型波动率预测精度的提升具有重要作用,然而上述波动率模型在不大量增加模型参数的前提下,并无法充分捕捉波动率的长记忆性,故存在一定的局限性。
受市场结构、交易机制和投资者构成等多方因素的影响,金融资本市场通常存在异质性特征(Muller等,1997)[10],导致资产波动呈现一定程度的相依性,即存在波动持续性(长记忆性),具体表现为波动序列存在正的和缓慢衰减的自相关函数。考虑到忽略长记忆性将导致模型无法准确地刻画长期波动率,Huang等(2016)[11]将包含日、周、月已实现波动率的HAR结构[12]引入波动方程,构建了能够捕捉波动长记忆性的Realized HAR GARCH模型,但HAR结构较为固定且回溯时间范围较短,无法刻画超过一个月的自相关性。为此,王天一等(2018)[13]利用混频数据抽样(Mixed Data Sampling,MIDAS)结构[14]改进Realized GARCH模型,能够有效地提取数据中的长期波动信息。Borup和Jakobsen(2019)[15]进一步将条件方差乘法分解为短期和长期成分,并引入MIDAS结构的长期波动方程,提出Realized EGARCH-MIDAS模型,该模型整合了Realized EGARCH与MIDAS模型各自的优势,在充分利用高频信息的基础上能够灵活有效地刻画资产收益波动率的聚集性与长记忆性,在实证中显示出较强的拟合效果和预测能力。然而,资产价格除了存在以上讨论的波动聚集性及长记忆性之外,还具有一些无法忽视的典型特征,如跳跃行为与其收益率波动的非对称效应。
在现实生活中,经济、政治和社会等各方面出现的突发事件不断影响着各国金融市场,这使得资产价格呈现出不连续的跳跃式变化,这种由异常消息冲击而导致的资产价格极端波动的现象被称为跳跃行为[16]。资产价格跳跃行为的研究首先需要解决的问题是如何识别与区分价格变动中的连续波动成分与跳跃成分。随着已实现测度渐近理论性质研究的不断深入,学者们基于高频数据在二次变差理论的框架下提出了众多非参数跳跃检验方法,包括Barndorff-Nielsen和Shephard(2004,2006)[17-18]提出的BNS跳跃检测法,Andersen等(2007)[19]提出的ABD跳跃检测法,At-Sahalia和Jacod(2009)[20]提出的ASJ检测法,Bollerslev等(2013)[21]提出的TOD检测法以及Andersen等(2012)[22]提出的ADS跳跃检测法等,而其中最为广泛应用的是ADS跳跃检测法,这一方法对跳跃及微观噪声同时稳健。在利用跳跃检测方法识别出显著性跳跃之后,已实现波动率可以分解为离散跳跃部分与连续波动部分。在此基础上,学者们开始研究这两个波动成分对于模型波动率预测的影响。Santos和Ziegelmann(2014)[23]、Ma等(2019)[24]在MIDAS模型中引入基于不同跳跃检测法得到的跳跃波动与连续波动,以此提升了原有模型的波动率预测精度。Pan等(2020)[25]则在Engle等(2013)[26]的GARCH-MIDAS模型中引入收益率的跳跃性,提出了GARCH-Jump-MIDAS模型。上述研究证实了在波动率建模中考虑跳跃行为的重要性,也由此启发本文进一步在Realized (E)GARCH模型框架下考虑跳跃行为对条件方差的影响,而Realized EGARCH-MIDAS模型长期方程中的MIDAS结构为在模型中引入跳跃波动提供便利。
此外,大量的实证研究表明金融资产收益率序列的波动常常存在非对称效应,即波动率对坏消息和好消息的反应不同。考虑到非对称效应是影响资产价格波动的重要因素,Nelson(1991)[27]将非对称效应引入GARCH模型,随后学者们[28-29]不断丰富非对称GARCH族模型,并在实证中检验了此类非对称模型在波动率拟合和预测上的良好性能。而在高频数据领域,波动非对称性的研究同样引起了学者们的关注。Barndorff-Nielsen等(2010)[30]区分正负收益提出已实现半方差(Realized Semi-variance,RS),将已实现波动率分解成上涨半方差(Positive Realized Semi-variance, RS+)与下跌半方差(Negative Realized Semi-variance,RS-),亦被称为“好”波动率与“坏”波动率[31],以刻画波动的非对称性。在此基础上,学者们将已实现半方差[32-33]引入包含已实现波动率的GARCH-MIDAS模型框架中,研究好坏波动率对未来条件方差的不对称冲击,并验证了考虑非对称效应能够提升模型的波动率预测能力。值得注意的是,Realized EGARCH-MIDAS模型的测量方程及波动方程中的杠杆函数也能够刻画收益率对条件方差的非对称性影响,但是忽略了长期方程中已实现波动率的非对称效应。因此,本文考虑将Realized EGARCH-MIDAS模型的长期波动方程中的已实现波动率分解为好坏波动率,以完善模型的非对称结构。
当前,在经济全球化、金融自由化及金融创新加速的背景下,金融市场波动率的影响因素越来越交错复杂,极端事件频繁发生,导致资产价格的跳跃性增强,收益的波动率也普遍呈现出长记忆性与非对称性。在这样的背景下,学者们[34-35]开始探讨在单一模型框架下同时研究以上这些因素对波动率的影响,而研究结果也证实同时考虑跳跃与非对称性能够提升模型的波动率刻画能力。为此,考虑到Realized EGARCH-MIDAS模型够很好地刻画波动率的长记忆特征,而已实现波动率既能分解为连续、跳跃波动,又能分解为好、坏波动率,本文提出Realized EGARCH-MIDAS模型的三组拓展模型,分别考虑跳跃、好坏波动率以及综合这两因素提出的正负跳跃与正负连续波动的影响,并在偏t分布的假定下将模型应用于国内股票市场,以沪深300指数为实证研究对象,综合刻画其收益率波动的聚集性、偏峰厚尾性、长记忆性与非对称效应以及价格的跳跃特征,并进一步比较各模型的波动率及风险预测能力。
本研究的主要贡献为:第一,运用稳健的ADS跳跃检测法识别沪深300指数价格序列每日的跳跃波动,并将之引入Realized EGARCH-MIDAS模型,以探究跳跃行为对条件方差的影响;第二,考虑波动的非对称效应,将模型长期方程中的已实现波动率分解为好波动率与坏波动率,以此完善Realized EGARCH-MIDAS模型的非对称结构;第三,根据已实现波动率的渐近理论性质,基于跳跃检验提取正负跳跃与正负连续波动,并引入Realized EGARCH-MIDAS模型中,以考虑跳跃行为与非对称效应的综合影响;第四,通过样本内拟合与样本外滚动预测,结合似然函数、信息准则与基于损失函数的DM、MCS检验法综合比较了以上模型在波动率估计和预测上的效果,并以此为基础进行风险度量。
本文其余部分结构安排如下:第二部分为理论介绍,包括已实现波动率的理论基础,以及波动率基础模型和本文提出的改进模型,并给出估计方法;第三部分基于以上理论进行实证研究,包括模型样本内的估计以及波动率、风险值的样本外预测,并对实证结果进行评估;第四部分概括主要研究结论并作出展望。
二、 理论与模型
(一) 已实现波动率的极限理论
自Black-Scholes期权定价模型提出以来,一般都假定资产价格过程服从连续路径,然而金融市场中不时出现的极端事件证实这一假设存在一定的局限性。为此,Merton(1976)[36]在连续路径的扩散过程中引入了不连续的跳跃过程对资产价格序列进行建模。在跳跃存在的无风险套利市场中,当资产对数价格Xs=log(ps)(ps表示s时刻的资产价格)服从连续时间跳跃扩散过程时,对数收益率在第t日的二次变差过程可以表示为:
(1)
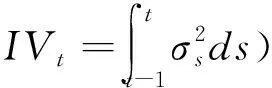
将每个交易日分为n个时间段,令Δ为价格数据的抽样间隔(n=1/Δ),第t日s时刻的对数收益率rs=Xs-Xs-Δ。已实现波动率由日内高频收益率的平方和定义:
(2)
Barndorff-Nielsen和Shephard(2002)[37]证实,若资产价格过程存在跳跃,已实现波动率依概率收敛于二次变差过程。因此,只要得到积分波动率IV的一致估计量,就可以剥离已实现波动率中的跳跃部分。
基于这一思路,Barndorff-Nielsen和Shephard(2004)[17]提出已实现双幂次变差(RBV)作为积分波动率的一致估计,并基于已实现波动率与已实现双幂差的差值进一步构建了BNS跳跃检测法[18]。然而,RBV对市场微观结构噪声及零收益率较为敏感,其估计的有偏性导致BNS检测缺乏稳健性。为此,Andersen等(2012)[22]基于最近邻截断方法构建对跳跃及微观噪声均稳健的中位数已实现波动率(MedRV)来估计积分波动率(IV):
(3)
(4)
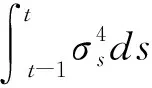
(5)
因此,可将已实现波动率分解为如下离散跳跃部分与连续波动部分:
(6)
(7)
其中,“+”表示取跳跃方差的非负值(负值则取为0),I(·)为示性函数,当括号中条件成立时取值为1,否则取值为0。
进一步,考虑到资产价格波动普遍存在非对称效应,Barndorff-Nielsen等[30]119-120为区分正负收益率提出上涨已实现半方差和下跌已实现半方差:
(8)
(9)
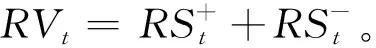
此外,在风险管理实践中,投资者对于正跳跃与负跳跃有着不同的态度和风险控制措施,分析正、负跳跃对波动率的影响有助于投资者更深入地了解股票市场的内在运行机制。因此,根据中位数已实现波动率(MedRV)与已实现半方差的渐近理论性质,将已实现跳跃波动分解为由正向收益驱动的正跳跃部分与由负向收益形成的负跳跃部分,剥离出的正跳跃与负跳跃可以分别记为:
(10)
(11)
由此也可以得到正连续波动部分与负连续波动部分如下:
(12)
(13)
(二) Realized EGARCH-MIDAS模型
为充分利用日内高频信息并同时捕捉波动率的长记忆性,Realized EGARCH-MIDAS模型利用乘法分量结构与MIDAS结构合理整合包含日内高频信息的已实现波动率与较低频率的变量,在实证中显示出较强的波动性刻画能力。滞后阶数p=q=1的对数Realized EGARCH-MIDAS模型为:
(14)
loght=βloght-1+τ(zt-1)+αut-1
(15)
(16)
(17)
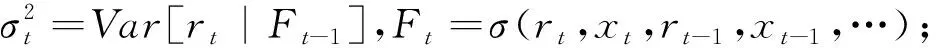
(18)
(19)
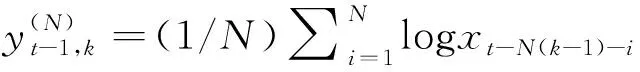
(20)
另外,MIDAS分量的滞后长度K的选择参照Borup和Jakobsen(2019)[15],采用K=52与K=12分别对应周线N=5与月线N=22,即考察总长度大约为一整年的滞后已实现波动率的影响。此外,值得注意的是,当长期方程中λ=0时,Realized EGARCH-MIDAS模型就退化为Realized EGARCH模型。在后文的讨论中,将Realized EGARCH模型与Realized EGARCH-MIDAS模型分别简记为REGARCH模型与REGARCH-MIDAS模型。
(三) Realized EGARCH-MIDAS模型的拓展
REGARCH-MIDAS模型借鉴GARCH-MIDAS模型的构建思路,将条件方差乘法分解为短期和长期分量以捕捉波动性,其中短期成分的动态特征与REGARCH模型保持一致,长期成分则引入MIDAS结构进行建模。值得注意的是,针对GARCH-MIDAS模型的长期方程,学者们提出了不同的改进形式,如引入影响波动的宏观经济变量[38-39],或是考虑波动率的跳跃行为[25]与非对称性效应[33]的影响等,这些改进均在一定程度上提升了模型的波动率预测效果。基于这一思路,本文将REGARCH-MIDAS模型的长期方程进行拓展,以提升模型整体的波动性刻画能力。具体来说,从跳跃性与非对称性两个角度进行改进。
首先,考虑跳跃行为对波动率的影响。在波动率模型的研究中,越来越多的学者关注于极端收益引起的跳跃行为对波动的影响,如孙洁(2014)[40]、Laurent和Shi(2020)[41]等。这些研究均表明,建立一个考虑跳跃影响下收益异常波动的波动率模型至关重要。为此,参考Ma(2019)[24]的建模思路,将REGARCH-MIDAS模型的长期方程式(17)的已实现波动率按照式(6)与式(7)进行跳跃分解,得到拓展后的长期方程为:
(21)
其次,探究波动率的非对称特征。参考Patton和Sheppard(2013)[31]的处理,将REGARCH-MIDAS模型长期方程式(17)的已实现波动率按照式(8)与式(9)分解为好坏波动率,得到拓展后的长期方程为:
(22)
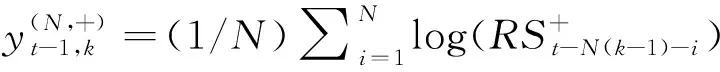
进一步,在同一模型框架内同时考虑跳跃行为与非对称性的影响,将REGARCH-MIDAS模型长期方程式(17)的已实现波动率按照式(10)至式(13)分解为正跳跃、负跳跃与正连续波动、负连续波动四个部分,得到拓展后的长期方程为:
(23)
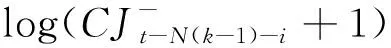
(四) 模型参数估计方法
本文采用极大似然法(Maximum Likelihood Estimation, MLE)对模型的具体参数进行估计,具体的估计步骤参考Hansen和Huang(2016)[5]。REGARCH-MIDAS族模型的对数似然函数可以表示为:
(24)
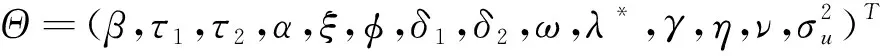
(25)
另外,参照王天一和黄卓(2012)[6]将收益残差zt的分布设定为零均值、单位方差的偏t分布,即zt~skt(η,ν),这一设定是基于金融市场收益率分布普遍存在的有偏及厚尾性质。在已知zt分布的基础上,进一步可由均值方程计算得到半对数似然函数t(rt;Θ)的表达式为:
(26)
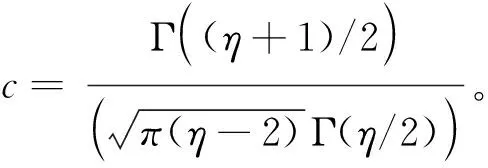
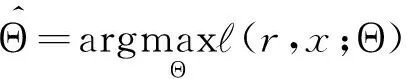
此外,将短期波动的初始值设置为其无条件均值,即logh0=0。为了初始化长期波动loggt,将MIDAS结构中滞后的对数已实现测度均取值为logx1。
三、 实证分析
在这一部分,我们研究REGARCH-MIDAS模型与基于跳跃、好坏波动率拓展的REGARCH-MIDAS-CJ模型,REGARCH-MIDAS-RS模型和REGARCH-MIDAS-RSJ模型的实证拟合效果及预测表现。首先选取实证数据,并进行初步的统计检验与分析,确认模型对于实证数据的适配性,在此基础上给出上述模型周线与月线设定下共8个模型的参数估计结果。进一步,对比这些模型在不同准则下的样本外预测性能,以探索引入跳跃与好坏波动率是否能提高REGARCH-MIDAS模型的预测能力。
(一) 数据选择与基本统计分析
沪深300指数作为衡量中国股市的最佳单项指标之一,被广泛应用于波动率模型的实证研究[8-9]中。本文选取沪深300指数的价格数据作为样本,时间跨度为2015年1月5日到2021年3月3日(共计1500个交易日),数据来源于JoinQuant数据库。此外,为减少微观结构噪声的影响,本文采用5分钟的取样频率,由此得到的高频数据总量为72000个(每天48个高频价格记录)。采用“收盘价—收盘价”计算对数收益率(数值放大100倍以便观测处理),并按照式(2)计算得到第t日的已实现波动率RVt。图1给出了指数序列的日收盘价、收益率和已实现波动率的时序图以及对数已实现波动率的自相关函数图。从图中可以看到,样本期内沪深300指数的价格波动比较明显,收益率序列也存在明显的波动集聚现象。选取的样本区间涵盖了指数价格的牛市、熊市与平稳期,比较有代表性。此外,对数已实现波动率的ACF呈现缓慢衰减的趋势,这表明波动具有持续性,存在一定的长记忆性。
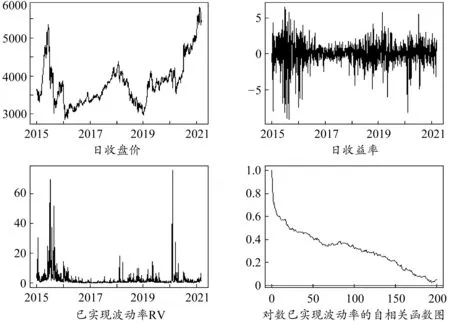
图1 沪深300指数日收盘价、日收益率和已实现波动率的时序图以及对数已实现波动率的自相关函数图
另外,表1列出了沪深300指数的日收益率和日对数已实现波动率的描述性统计信息。从J-B检验的结果,结合偏度与峰度值,可以看出收益率与对数已实现波动率的分布均偏离正态分布,这说明设定模型残差服从非正态分布的合理性。ADF检验的结果显示两个序列均不存在单位根过程,可以判定序列都是平稳的。Ljung-Box检验证实,两个样本序列均存在明显的自回馈效应,可以进一步证实沪深300指数的波动存在长记忆特征。此外,对数收益率的单样本t检验的p值为0.604,可以判定收益率的均值是显著等于零的,那么在模型的收益方程剔除常数项是合理的。

表1 沪深300指数日对数收益率序列和对数已实现波动率的描述性统计
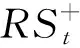
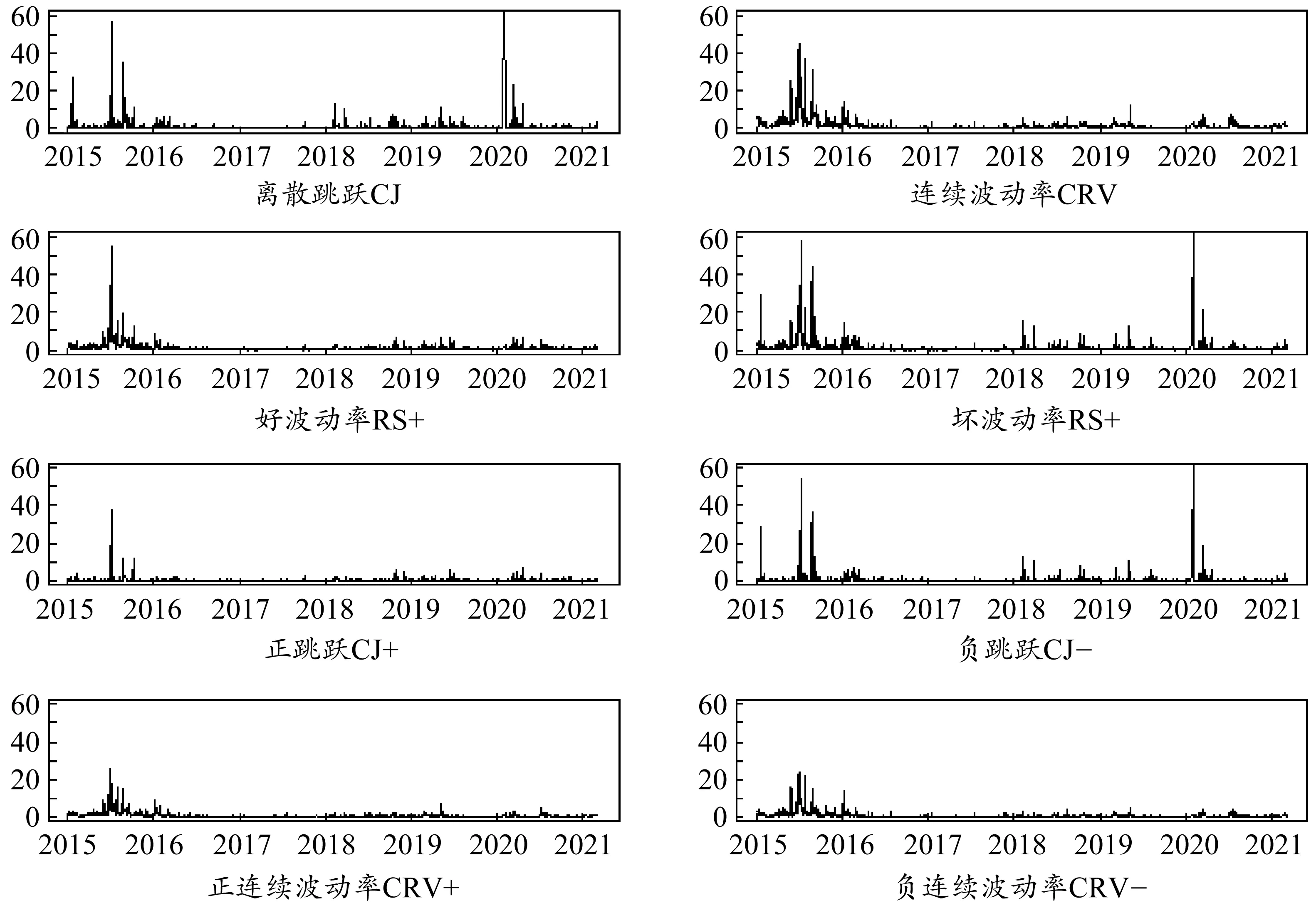
图2 沪深300指数各日波动率序列的时序图
从图2可以发现,各序列均存在明显的波动聚集现象,在2015年至2016年这段时间普遍出现大幅波动。具体来看,样本期内沪深300指数的离散跳跃分布密集,计算得出跳跃显著的交易日共计480日,占比超过30%,而连续波动率的聚集性相比跳跃会更强一些。此外,沪深300指数在样本期内由负收益构成的坏波动率相较受正收益影响的好波动率振幅更大,但收益波动出现负跳跃的天数要小于出现正跳跃的天数。从图中还可以看到,2020年初由新冠肺炎疫情引发的指数波动的主要成分为离散跳跃,而且这一波动主要是由负收益导致的,即负跳跃。
(二) 样本内估计与结果分析
在本节,基于沪深300指数的全样本数据,对周线与月线(周线:N=5,K=52;月线:N=22,K=12)设定下的REGARCH-MIDAS模型与拓展的REGARCH-MIDAS-CJ模型、REGARCH-MIDAS-RS模型与REGARCH-MIDAS-RSJ模型共计8个模型进行参数估计,并利用似然函数与信息准则来评估模型的拟合效果,具体的估计结果见表2。
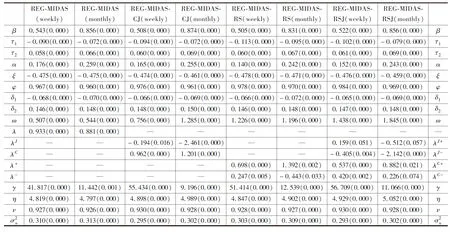
表2 模型参数估计结果

(续表2)
接下来,根据表2的估计结果,从以下几个角度展开分析:
1.总体拟合效果分析。从表2可知,已实现波动率无论按照周线还是月线聚合,相比REGARCH-MIDAS模型,基于跳跃、好坏波动率改进的三个模型在全似然值(r)与信息准则AIC与BIC上均有更好的表现,其中REGARCH-MIDAS-RSJ模型的样本内表现最优,这说明将长期方程中的已实现波动率进行分解能够提升REGARCH-MIDAS模型的整体拟合效果,而同时考虑波动率的跳跃性与非对称性对模型拟合效果的提升最大。另外,周线下的REGARCH-MIDAS族模型普遍比月线下的同类模型拥有更优的总体拟合表现,这一结果与Borup和Jakobsen(2019)[15]的研究一致。
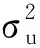
3.跳跃波动与连续波动的贡献分析。由表2可知,REGARCH-MIDAS-CJ模型中,参数λJ与λC均显著且符号相反(λJ为负,λC为正),说明历史的跳跃波动信息对于沪深300指数收益的条件方差在长期来看具有抑制作用,而持续较高的连续波动则会导致较高的长期波动性。另外,按月线聚合的已实现波动序列相比周线对于条件方差的持续性影响相对更强一些。以上结果显示,当沪深300指数收益率出现显著的跳跃时,可能会导致收益波动的短期震荡,但长期来看这种影响持续较短,股票市场的长期波动主要来源于收益率的日常连续波动。
4.好坏波动率的贡献分析。表2中REGARCH-MIDAS-RS模型的参数λ+和λ-都是显著的,说明沪深300指数的好坏波动率具有不对称的波动冲击,而λ+显著为正,且显著性和绝对值都高于λ-,说明由日内正向收益形成好波动率相比由日内负向收益形成的坏波动率对收益率条件方差的长期影响更强。同样,按月线聚合的已实现波动序列相比周线的持续性影响相对更强。以上结果显示,沪深300指数收益的长期波动性与过去的好波动率的关系更密切,这是因为正收益导致的持续好波动率使得投资者在长期时间范围内期望股价继续上涨,而对市场的波动造成更持久的影响。
5.正、负跳跃的贡献分析。表2中REGARCH-MIDAS-RSJ模型的参数λJ+和λJ-显著,说明沪深300指数的跳跃波动存在非对称性,而λJ-显著为负,且显著性和绝对值都高于λJ+,说明由负收益导致的负跳跃对于沪深300指数收益的长期波动具有明显的负向冲击,而正跳跃对波动的持续性影响相对较弱。另外,参数λC+和λC-显著为正,但λC+的显著性和绝对值要高于λC-,说明正、负连续波动对于沪深300指数的长期波动都具有正向影响,且正连续波动的影响更大。对于这些结果一个可能的解释是我国股票市场的投资者对于收益率波动的正跳跃和负跳跃存在不同的态度,当股票价格大幅下跌时,虽然短时间内会造成较大的波动,但长期来看会降低投资者的市场参与积极性,导致负跳跃的影响程度逐渐降低,而出现收益的正跳跃时,投资者往往会情绪高涨,市场参与度随之上升,从而对波动性造成持续性影响。
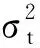
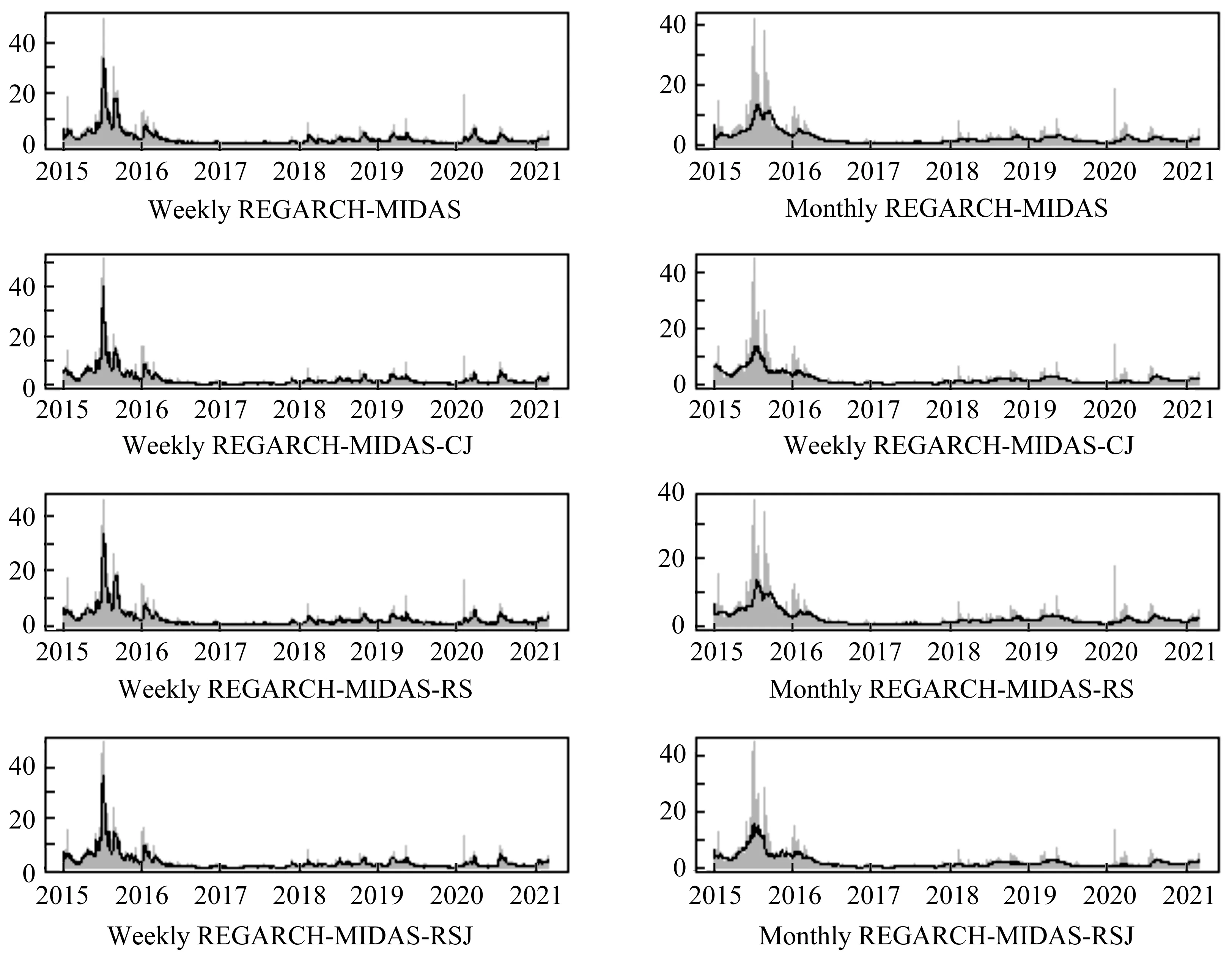
图3 各模型的拟合条件方差以及长期波动gt时序图
(三) 条件方差的自相关函数
为了更清晰地展示以上模型对于波动持续性的刻画能力,本节通过自相关函数(ACF)图来研究比较各个模型的自相关结构。图4展示了周线下REGARCH-MIDAS模型及其拓展模型的对数条件方差的模拟ACF和样本ACF。其中实线为模型通过样本实际拟合得到的条件波动率的样本ACF(SACF),虚线则为利用表2中的估计参数获得的模拟ACF(月线下每个模型的ACF图形及相关结论与周线下类似)。其中,模拟选择的样本长度为2000(约8年),在上文定义的残差分布下分别进行10000次Monte Carlo模拟。一般来说,模拟的ACF与样本ACF靠得越近,则理论模型与实际模型之间的内部一致性就越高,能够更好地捕捉条件方差的相依结构。
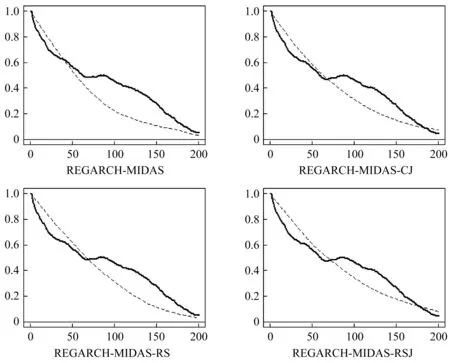
图4 周线下各模型对数条件方差的模拟(虚线)和样本(实线)自相关函数
从图4可以看到,引入乘法分量结构的REGARCH-MIDAS族模型能够在较长时间范围上捕捉波动率的相依性,总体而言这种刻画能力在滞后70期范围内更佳。此外,相比REGARCH-MIDAS模型,基于跳跃、好坏波动率改进的三个模型的模拟ACF与样本ACF曲线整体上都更接近,这说明本文提出的改进模型在一定程度上具有更强的波动率长记忆性捕捉能力。另外,REGARCH-MIDAS-CJ和REGARCH-MIDAS-RSJ模型的两条ACF曲线在滞后70期至200期的范围内比较靠近,其中REGARCH-MIDAS-RSJ模型的ACF曲线最为贴近,说明在模型的长期波动方程中考虑跳跃分解能够比较明显地提升模型在长期范围内捕捉波动持续性的能力。
(四) 样本外波动率预测及检验结果
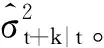
(27)
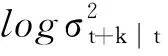
(28)
因此,已知t时刻的ht,ut和zt就可以直接计算短期成分对预测的贡献。为了获取长期成分gt+k|t,本文通过模拟方法来获得预测值,首先采取bootstrap方法从zt和ut的经验分布(在同一历史观察窗口中获得)中重新采样,并利用测量方程(16)计算得到已实现波动率的预测值,然后通过长期方程估计的参数递归得到长期波动的预测值。需要说明的是,对于REGARCH-MIDAS-CJ模型,在得到已实现波动率的预测值后,需重新进行一次跳跃检验(仍采用ADS检验,且其中的MedRV与MedTQ由前日的原样本数据计算得到)以将其分解为跳跃波动与连续波动;同样,对于REGARCH-MIDAS-RS模型,也需要将得到的已实现波动率预测值进一步分解为好、坏波动率,两者具体的比例与前日原样本数据计算的两个指标的比例一致;REGARCH-MIDAS-RSJ模型则需进行跳跃分解与非对称分解两个步骤。最后,在进行M次(M=10000)模拟后得到预测的条件方差为:
(29)
接下来,与学者们之前的研究(王天一,2018[13];Borup和Jakobsen,2019[15])保持一致,在稳健损失函数族中选取对称损失函数均方误差(MSE)和非对称的准似然函数(QLIKE)来评估预测性能。损失函数的表达式如下表示:
(30)
(31)
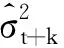
为了评估本文提出的三个改进模型是否显著地提升了REGARCH-MIDAS模型的预测性能,进一步进行Diebold-Mariano检验。DM检验对两组模型的预测值损失函数进行比较,检验其中一组模型预测的损失函数是否比另一组有显著减小,原假设为两个模型具有相同的预测精度,备择假设为第二组模型的预测精度更高,具体的统计量定义如下:
(32)
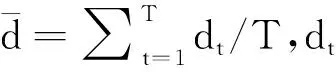
表3给出了以上8个不同波动率模型的样本外滚动预测的损失函数结果,以及6个改进模型相对基准REGARCH-MIDAS模型的损失函数DM检验结果。
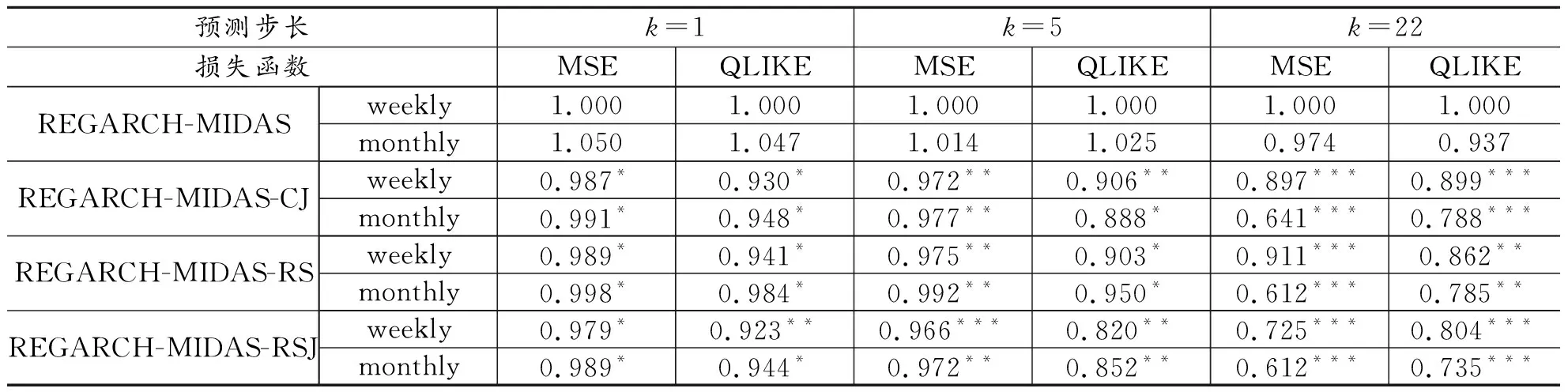
表3 REGARCH-MIDAS模型与对应拓展模型样本外波动率预测的损失函数及DM检验结果
注:表中的数值为损失函数标准化的结果,具体方法参考陈声利等(2018)[34],以REGARCH-MIDAS(weekly)模型为基准模型,将其余模型的损失函数均值除以基准模型的损失函数均值,值小于1表示对应模型的预测能力有所提高,加粗表示对应模型的损失函数均值最小。*表示相应的损失函数DM检验对应p值小于0.1,即在10%的水平下认为损失函数存在显著的差异,相应地**与***分别表示对应p值小于0.05与p值小于0.01
从表3可得,在所有预测范围上,同一时间线下,基于跳跃、非对称拓展的REGARCH-MIDAS-CJ模型、REGARCH-MIDAS-RS模型与REGARCH-MIDAS-RSJ模型的两个损失函数均值皆比对应的REGARCH-MIDAS模型的更小,结合DM检验结果(均至少在0.1的水平下具有显著差异),可以说明本文提出的改进模型均显著改善了REGARCH-MIDAS模型的预测性能,且在预测期较长时,改进效果更为显著(相应p值更小),而其中REGARCH-MIDAS-RSJ模型相比单独考虑跳跃行为或非对称效应的另外两个改进模型对原有模型预测精度的提升更加明显。另外,表3的结果显示,随着预测步数的增加,损失函数的比值逐渐减小,这表明在模型中引入时间推移的MIDAS结构是有效的,能够明显地提升模型在长时间范围上的预测精度。值得注意的是,在短期预测步长上(k=1,k=5),周线下的模型比月线下的对应模型普遍拥有更小的损失函数均值,而在长期预测步长上(k=22),月线下的模型预测表现相对更优。
值得注意的是,在采用某种损失函数作为模型的评判标准时,可能会存在波动率模型优劣的错误判断问题(Hansen和Lunde,2005)[45]。为使本文的研究结论有更强的稳健性,进一步进行“模型可信集”(Model Confidence Set,MCS)检验。MCS检验是Hansen等(2011)[46]提出的一种基于损失函数的模型检验方法,其检验的过程如下:
第一步,设M0为最开始用于比较的m0个模型构成的集合,按照损失函数的定义计算第i个模型的损失函数值Li,h,i=1,…,m0,h为预测序列长度,并计算任意两个模型u和v预测值的相对损失函数值duv,h;
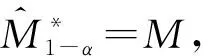
第三步,对于新的模型集合M,重复第二步,在每一次等价检验δM中原假设可以统一表示为:
H0,M∶E(duv,h)=0,for allu,v∈M⊂M0,
并按剔除准则eM在模型集中进行持续的检验,直到没有模型被剔除该集合为止,得到“最优模型集”。
此外,参照Hansen等(2011)[46],本文采用Bootstrap法来获得统计量TR和TSQ的估计值及相应的p值,且检验的控制参数按如下设置:块长度k由对所有损失差异进行自回归处理后得到的最大有效参数数确定;模拟次数B=10000次;检验的显著性水平α取值为0.1。表4展示了所有模型波动率预测的MCS检验结果。从表4可知,在10%的显著性水平上,大部分模型在两种损失函数下的不同步数波动率预测通过了MCS检验,这说明REGARCH-MIDAS族模型能够很好地预测沪深300指数收益率的波动情况。具体来看,本文基于跳跃、好坏波动率拓展的三个模型在日(k=1)、周(k=5)、月(k=22)三个预测范围内均改进了原始REGARCH-MIDAS模型的预测性能,具体体现在MCS的检验p值都更大。这说明本文对于REGARCH-MIDAS模型做出的改进能使得其在预测精度方面得到提升。其中,REGARCH-MIDAS-RSJ模型的预测效果是最好的(成为预测最优模型的次数最多),这说明在REGARCH-MIDAS模型的长期方程中同时考虑跳跃与非对称性的影响,能够使模型的波动率预测准确性得到实质性的改进。另外,对于较短时间范围的波动率预测(日、周),周线下的模型普遍拥有更好的预测表现;而对于月度这种较长时间范围的预测,月线下的模型能够提供更准确的预测结果。
综合以上所有检验结果(表3、表4)上可知,相比REGARCH-MIDAS模型,本文基于跳跃、好坏波动率提出的三个拓展模型能够为沪深300指数提供更准确的收益率波动预测结果,且预测表现最优的是综合考虑这两个因素的REGARCH-MIDAS-RSJ模型。这一预测性能的提升可能在于:拓展的模型包含反映跳跃引起的大幅波动信息(REGARCH-MIDAS-CJ),或者包含关于收益波动的非对称信息(REGARCH-MIDAS-RS),又或者考虑正、负跳跃的波动信息(REGARCH-MIDAS-RSJ),而这些丰富的信息能够提升模型对长期波动的刻画,进而对条件方差的预测产生影响。
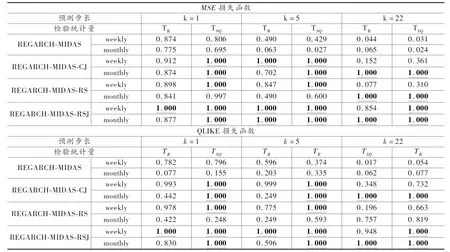
表4 不同模型波动率预测的MCS检验结果
(五) 风险值的预测及检验
考虑到对于投资者与监管机构而言,资产的最大损失是较为直观地反映资产风险的指标,所以本节在波动率预测的基础上,通过计算VaR与ES这两个风险度量指标来进一步判断以上模型的预测效果。
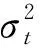
(33)
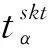
在实际的风险管理中,VaR经常低估真实损失,为此引入期望损失[48](Expected Shortfall,ES),其定义为损失超过VaR时的预期损失:
ESt+1=E(rt+1|rt+1≤VaRt+1)
(34)
由此,利用上文得到的向前一步条件方差预测值,采用文献研究中常用的5%的覆盖水平,通过公式(33)与(34)可以计算得到沪深300指数样本外的一步预测风险值VaR与ES。
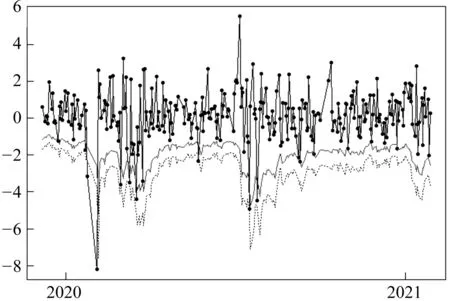
图5 预测区间沪深300指数对数收益率及其预测风险值时序图
图5展示了预测区间沪深300指数的样本对数收益率以及由REGARCH-MIDAS-RSJ(Weekly)模型计算得到的对应预测风险值,其中实线为VaR预测值,虚线为ES预测值。可以看出,在预测区间内,由REGARCH-MIDAS-RSJ(Weekly)模型预测的风险值与样本收益率波动形态一致,且能够覆盖大部分的负向收益。经过进一步计算可得,预测区间内VaR预测失败的天数占总预测天数的比例(失败率)约为0.047,接近给定的覆盖率α,且通过了后验测试,条件覆盖(Conditional Coverage,CC)检验[49]的p值约为0.858。以上结果说明REGARCH-MIDAS-RSJ(Weekly)模型产生了有效的VaR风险预测(其余模型也均通过了VaR的后验测试,详细结果限于篇幅未列出)。
接下来,为评价和比较各模型的VaR预测效果,进一步进行损失值检验。首先,采用分位数损失函数[50](Quantilie Loss, QL)来评价各模型预测VaR的能力,具体定义如下:
QLα=(α-Lt+1)(rt+1-VaRt+1)
(35)
其中,Lt+1=I(rt+1 其次,为了评估以上模型预测VaR和ES的综合能力,采用Fissler和Ziegel(2016)[51]提出的FZ损失函数,并进一步参考Patton等(2019)[52],假定VaR与ES严格为负,且满足ESt+1≤VaRt+1<0,由此得到以下损失函数: (36) 同样,为了更稳健地评估不同模型的风险预测能力差异,在如上定义的两类损失函数下,进行MCS检验,检验结果如表5所示。 表5 不同模型风险值预测的MCS检验结果 从表5的检验结果可知,在10%的显著性水平下,所有模型均通过了MCS检验,且有较多的模型MCS检验p值为1,这说明利用REGARCH-MIDAS族模型来预测沪深300指数收益率的风险值是稳健的,此类模型是一个很有效的股票市场风险测度工具。此外,周线下的模型相比月线下的对应模型普遍提供了更准确的样本外一步的风险预测值,其中本文提出的三个拓展模型(Weekly)在两种损失函数下的MCS检验p值均为1,显示了十分卓越的风险预测能力。综合来看,三个拓展模型(REGARCH-MIDAS-CJ、REGARCH-MIDAS-RS与REGARCH-MIDAS-RSJ)出现最优预测(MCS检验p值为1)的次数都比REGARCH-MIDAS模型(1次)更多,分别为5次、4次与7次,这说明本文将REGARCH-MIDA模型进行跳跃、非对称拓展能够提升原有模型的风险预测能力,预测精度最高的模型是REGARCH-MIDAS-RSJ模型,这也说明在同一模型框架下同时考虑跳跃与非对称性的对于模型风险预测能力的提升最大。 在高频金融数据建模的背景下,考虑到金融资产价格普遍存在的跳跃行为,以及收益率波动的长记忆性与非对称性,本文基于跳跃、好坏波动率对REGARCH-MIDAS模型进行拓展,提出REGARCH-MIDAS-CJ模型、REGARCH-MIDAS-RS模型与REGARCH-MIDAS-RSJ模型,提升了模型对收益率条件方差的刻画能力。以沪深300指数价格高频数据为样本,应用以上模型实证分析揭示了中国股票市场的波动性规律,进一步对收益率的波动性与风险值进行预测,以损失函数的DM及MCS检验来考察所提出的模型是否能达到更高的预测精度。其中,模型的改进基于三种形式的已实现波动分解:连续波动与跳跃波动、好与坏波动率以及正负跳跃与正负连续波动。此外,考虑到收益的偏峰厚尾性,设定残差服从偏t分布,并利用稳健的ADS检测法来甄别跳跃。本文的实证结果及相关结论有如下几点: 首先,样本内结果表明,本文提出的REGARCH-MIDAS拓展模型均能够更好地捕捉波动率的长记忆性,由此提升了原模型的整体估计表现,且REGARCH-MIDAS-RSJ模型的样本内表现最佳,即同时考虑跳跃与非对称波动的影响对模型的拟合效果提升最大。另外,周线下的REGARCH-MIDAS族模型普遍比月线下的同类模型拥有更优的样本内估计效果。参数估计结果显示,沪深300指数的长期波动主要来源于收益率的日常连续波动而非跳跃波动,其中由正向收益形成的正连续波动的影响更大;另外,沪深300指数的波动具有明显的杠杆效应,负向(正向)收益的冲击会加剧(抑制)短期波动,而负跳跃对于指数的长期波动具有明显的负向冲击。 其次,样本外波动率滚动预测的损失函数及DM与MCS检验结果显示,REGARCH-MIDAS族模型能够提供比较准确的沪深300指数收益率波动的预测值。相比REGARCH-MIDAS模型,本文提出的三个拓展模型在预测性能上均有所提升,而REGARCH-MIDAS-RSJ模型的预测效果是最优的,这说明将REGARCH-MIDAS模型长期方程中的已实现波动率同时进行跳跃与非对称分解能够使模型的预测准确性得到实质性的改进。另外,对于REGARCH-MIDAS族模型,周线下的模型能够提供更准确的日、周(短时间)波动率预测,而对于月度这种较长时间范围的预测,月线下的模型预测精度更高。 最后,风险值预测及相应的损失函数MCS检验结果显示,REGARCH-MIDAS族模型是很有效的风险预测工具,而本文基于跳跃、好坏波动率提出的三个拓展模型均显示了十分卓越的风险预测能力,其中预测精度最高的是REGARCH-MIDAS-RSJ模型,这也说明在同一模型框架下同时考虑跳跃与非对称性对于模型风险预测能力的提升最大。 综合以上研究结论,本文最主要的贡献在于进一步扩展和丰富了REGARCH-MIDAS模型,引入了跳跃和好坏波动率以完善原有模型的波动性结构,并证实改进后的模型能够为沪深300指数提供更准确的波动率预测结果,为市场参与者进行风险管理提供参考。本文提出的模型是基于混频数据建立的,不仅包含日内高频价格信息,还融合了日、周、月的已实现波动信息,并在模型的改进中进一步细分了长期波动率的波动形式,或是跳跃引起的大幅波动信息,或是关于收益波动的非对称信息,或是综合考虑这两种信息,而这些丰富的信息能够提升模型的波动率预测准确性。在之后的研究中,可以在模型中引入更丰富的已实现测度,如广义已实现测度等,或者在长期方程中进一步融合其他对波动有影响的外生变量,如宏观经济变量、不确定性变量等。另外,也可将创新的模型应用于其他资产(如债券、汇率、商品期货等)的波动性研究,并可进一步利用模型来进行投资策略选取、衍生品定价等金融应用。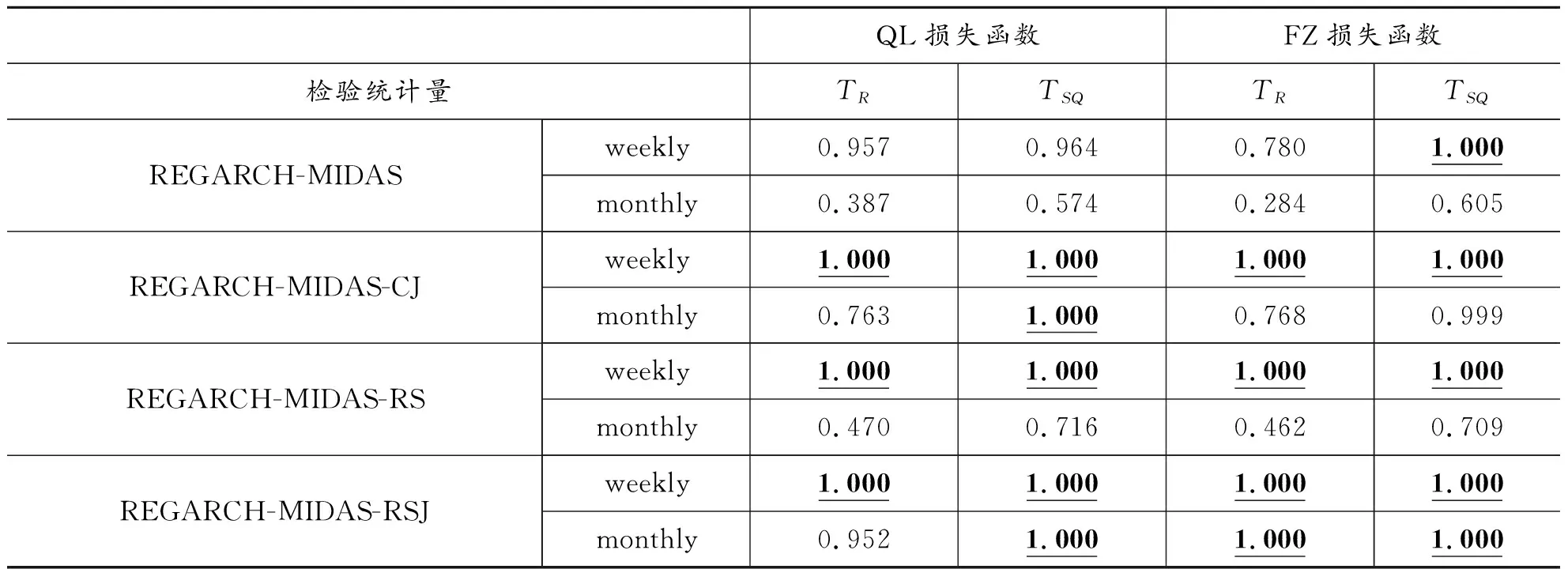
四、 结论及展望
