东营凹陷湖盆陡坡带砂砾岩储层评价方法及应用——以LA区块沙四上亚段为例

王 锦，冯国奇，王 鑫

（1.中国石化中原油田分公司物探研究院，河南 濮阳 457001；2.中国石油大学（华东）地球科学与技术学院，山东 青岛 266580）

砂砾岩储层在油气勘探开发过程中占据重要地位，尤其在我国东部的中、新生代陆相断陷湖盆的东营凹陷北部陡坡带发育大量砂砾岩储层，获得了可观的工业油流［1-4］。研究区LA区块滚动勘探开发时间较短，对砂砾岩储层的认识相对薄弱。此外，砂砾岩储层内部结构复杂，各影响因素间多呈非线性关系。储层非均质性是决定储层质量的关键因素［5］，影响油田开发效果。砂砾岩储层纵向上砂体间储层性质差异程度多变，导致单因素表征层间非均质性的角度各异性明显，开展储层质量评价工作难度较大。

目前，国内外学者针对储层质量及储层非均质性评价开展了大量的研究。杨少春［6］利用熵权法对数值存在差异的属性参数进行去同存异处理，以非均质综合指数定量表征储层非均质性；严科［7］针对非均质定量表征角度各异性问题，提出基于储层物性参数累积分布特征的新参数进行储层宏观非均质表征；宫清顺［8］借助地质、测井、生产动态等资料，从孔隙结构、渗透率韵律、夹层类型及分布样式、有效砂体结构及连通模式入手，深入剖析砂砾岩储层宏观、微观非均质性主因并对其表征。储层质量和非均质性评价方法大多是利用模糊数学或灰色理论对多储层评价因素做不确定性评价，针对砂砾岩储层纵向上砂体间储层性质差异程度多变性和内部结构的复杂性，若只考虑单一评价方法，评价结果间的差异性难以得到良好体现。因此，优选非均质评价指标，联合熵权法及模糊层次分析法，通过构建熵权、模糊互补判别矩阵，有效扩大评价结果的差异性和解决角度各异性，进而实现砂砾岩储层层间非均质性定量表征；然后针对储层质量与各储层评价参数间的非线性关系，利用极具灵活性和自适应性的BP神经网络法构建复杂函数关系，从而划分砂砾岩储层类型，客观有效地实现砂砾岩储层质量评价和储层平面展布预测。

1 概况

东营凹陷北部陡坡带面积约1 500 km2，具有坡度陡、物源和油源供应充足的特点［9］，构造上整体受陈南和滨利两套断裂带系统控制［10］，形成“北断南超”、山高谷深、沟梁相间的古地貌特征［11］。研究区LA区块处于陡坡带的西段二台阶，北为陈家庄凸起，西邻滨县凸起，东邻民丰洼陷，南为利津洼陷，北部靠近物源区陈家庄凸起（图1）。根据试油资料显示，研究区沙四上亚段的7、8砂组为主力含油层，7砂组可划分为8个小层，8砂组可划分为7个小层。岩性以砾岩、含砾砂岩、中-粗砂岩和暗色泥岩为主，具有空间上混杂堆积、相变快、物性差、储层非均质性强的特点［12-14］。研究区砂砾岩储层成分成熟度较高，岩石组成以长石岩屑砂岩为主；储层平均孔隙度为8.56%，平均渗透率为4.73×10-3μm2，属于低孔、低渗储层（图2）。

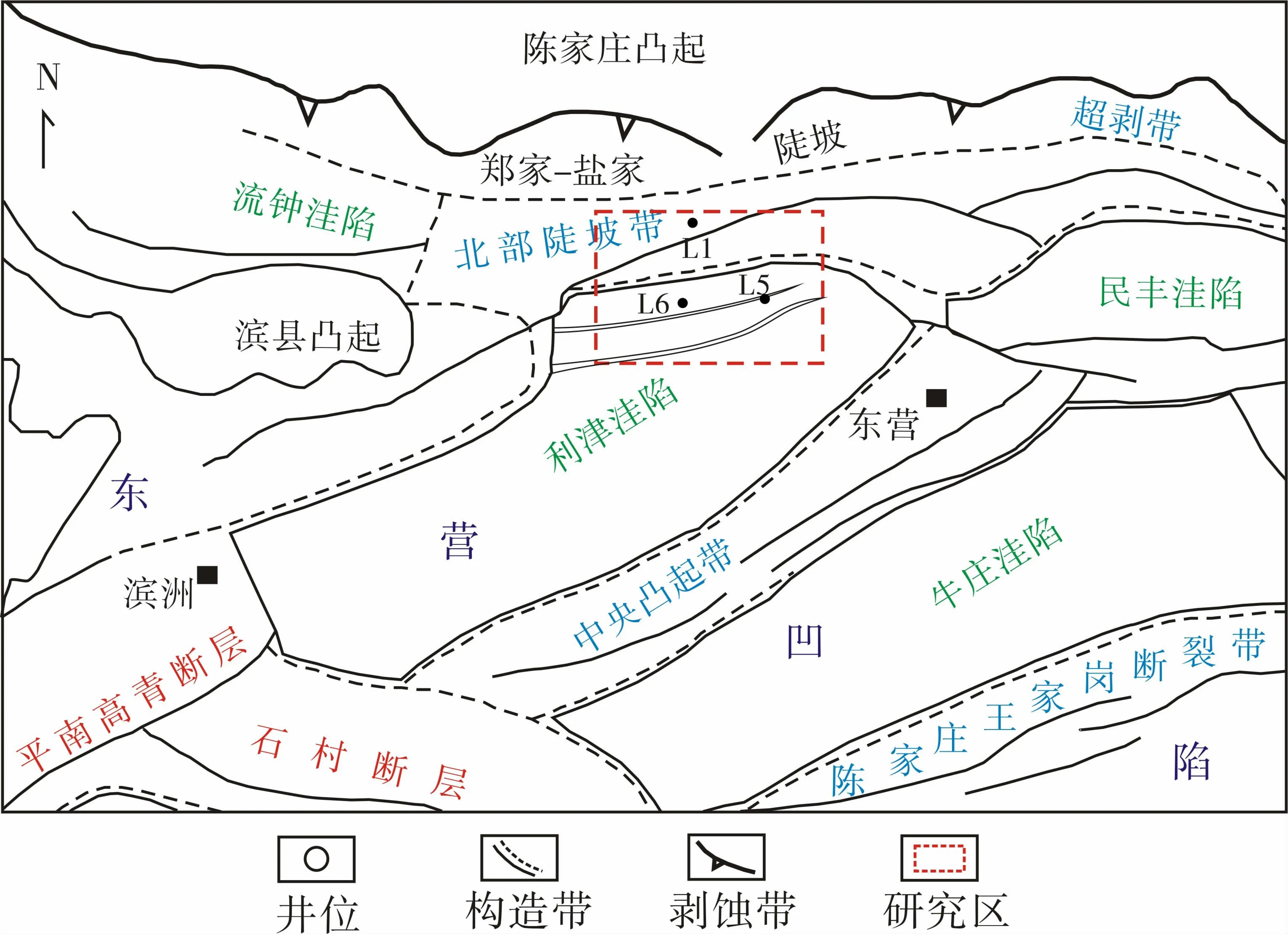
图1 研究区构造位置

图2 LA区块沙四上亚段岩性分类及岩心分析孔隙度、渗透率分布频率

2 层间非均质性表征

储层层间非均质性是指储层在纵向上砂体间储层性质的差异程度［15］，是影响储层质量的关键因素之一，由于砂砾岩储层差异程度的多变性受多种因素控制和影响，导致储层层间非均质性表征难度增加。针对该问题，文中通过联合熵权法及模糊层次分析法进行定量表征。

2.1 表征思路及实例应用

熵权法是一种客观赋权的方法，主要通过熵值来确定指标的重要程度，最大特点为“去同存异”，使得数值差别不大的属性对非均质综合指数弱化，差别较大的属性对非均质综合指数强化。通常指标熵值越小，差异系数越大，差别程度越强，其权重越大［6，16］。研究区以砂砾岩储层发育为主，该类储层相对常规储层的评价指标数值间差异性更小，单从熵权法出发，难以有效扩大评价结果的差异性，因此将其与模糊层次分析法［17］相结合，得到各个指标的熵值之后，再考虑不同熵权之间的相互关系，求取各个指标相应的熵权的客观权重，进而得到非均质综合指数，该结果可有效扩大不同层位之间指数的差异性，取得更好的评价结果。

基本算法如下：

①确定对象集合。确定LA区块需要评价计算的各井集合，记为：

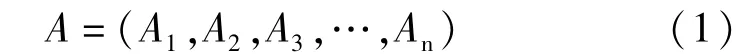
②确定指标因素的集合。熵权法与主成分分析法思路相近，可筛选出对非均质贡献突出的参数指标并赋予较大熵权［6］。同时，保证选取的指标涵盖评价储层层间非均质性的多个方面且各指标间相互独立。选取重要参数有：孔隙度、渗透率（代表储层储集、渗流能力）、渗透率变异系数（代表储层渗透率离散程度）、储层厚度（代表储层实际发育情况）、夹层厚度（代表对储层油气阻挡能力）［18］，记为：

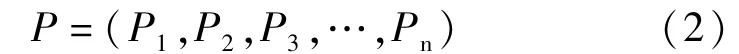
式中：P1=a11a21…an1，P2=a12a22…an2，P3=a13a23…an3，Pm=a1ma2m…，anm

③确定指标矩阵。矩阵元素为属性参数，aij表示i井对应j参数的数值。

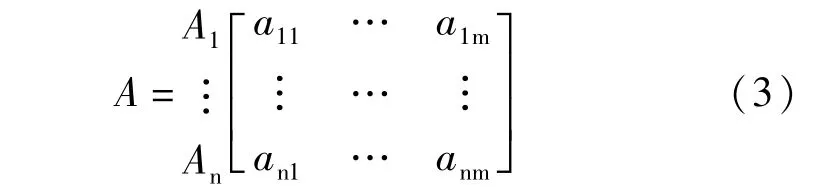
④指标值标准化，将矩阵A中aij经标准化处理后得到bij，从而确定矩阵B。其中对于渗透率、孔隙度、储层厚度值越大，对应的层间非均质性越弱，则使用式（4）做标准化处理；对于渗透率变异系数、夹层厚度值越大，对应层间非均质性越强，则使用式（5）作处理。

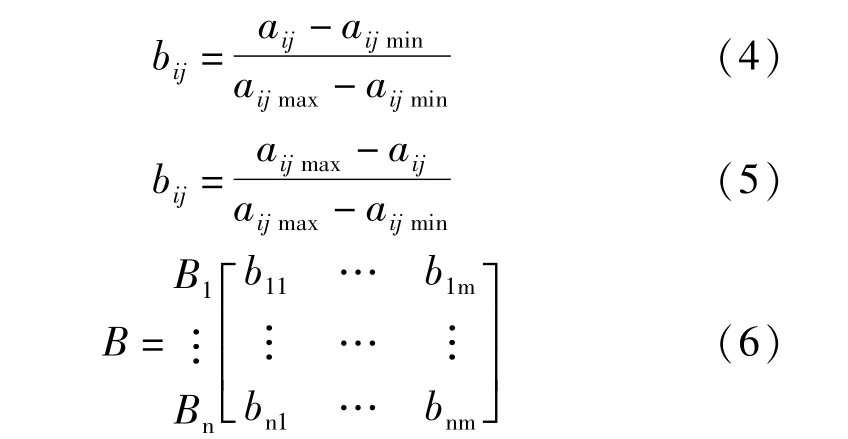
⑤计算各指标的熵值H。利用式（7）求取式（8）中各个指标的熵值。

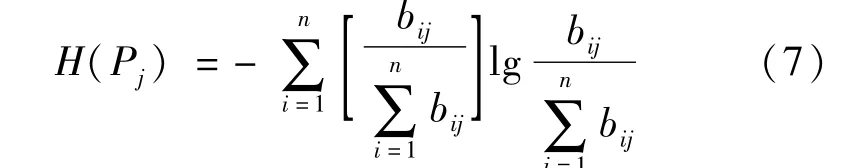
根据熵的极值性，当各指标的水平值越接近，其熵值越大。因此用最大熵值H（Pj）max=lg n对公式（7）所得到的熵值进行归一化处理，得到表征指标Pj的相对重要程度的信息熵E（Pj）。

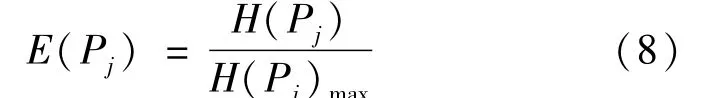
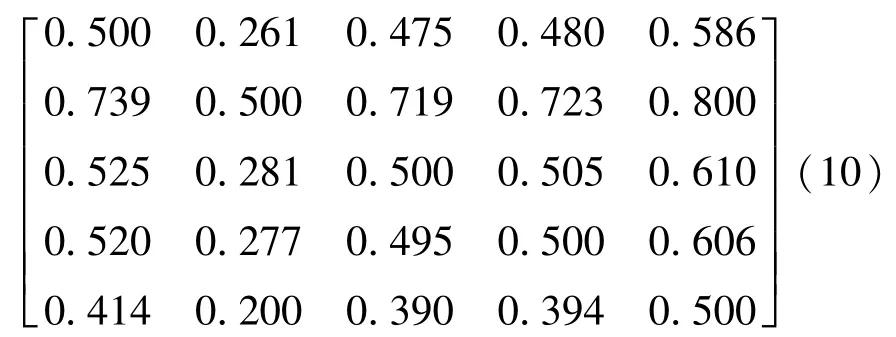
⑥考虑不同熵权之间的相互关系，将其与模糊层次分析法结合，以E2s417-1小层为例，利用公式（9）构建由熵权得到的模糊互补判断矩阵（10）。

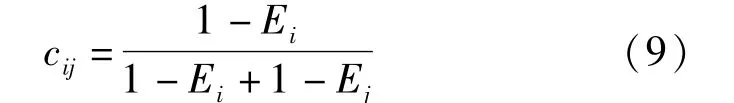
对于模糊互补矩阵，满足0≤cij≤1，且cij+cji=1，cij=0.5表示指标i和指标j同等重要，cij＞0.5表示指标i重要性高于指标j，反之亦然。若cij=cik+ckj+0.5，则该矩阵为模糊一致判断矩阵［19］。

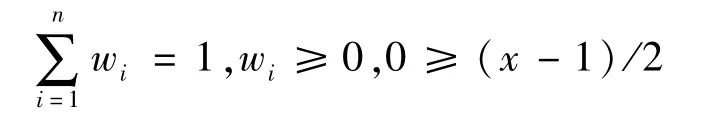
式中：wi为第i种指标的客观权重，无量纲；x为指标个数；θ为调整系数，该值越小，权重之间的差异越大，代表重视指标间程度的差异。

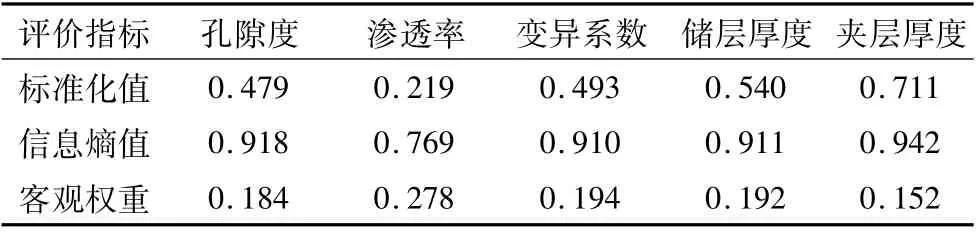
表1 LA区块E2 s41 7-1小层非均质性评价指标客观权重值

⑧计算非均质综合指数I：

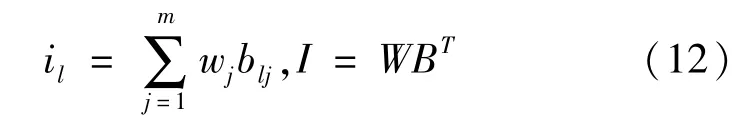
式中：W为权重向量；T表明矩阵转量，0＜I＜1，I值越小，表示非均质性越强；反之亦然。

2.2 综合熵权法与模糊层次分析法的储层层间非均质性评价

分别用熵权法和综合熵权法与模糊层次分析法计算LA区块沙四上亚段7砂组和8砂组主力层内各个小层非均质评价指数，并对其结果进行统计（图3a、3b）。由图3a可以看出，E2s418-2、E2s418-3小层非均质性较强，E2s417-3、E2s417-4小层非均质性较弱。

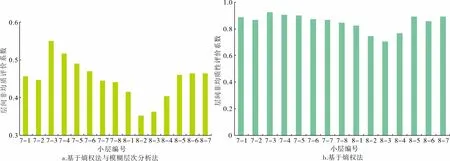
图3 LA区块沙四上亚段储层层间非均质综合指数

与单一利用熵权法（常规方法）表征砂砾岩储层层间非均质性相比，基于熵权法与模糊层次分析法的储层层间非均质综合指数能够克服传统方法的各参数表征角度各异、评价指标无边界、各参数评价结果相互矛盾等问题，有效扩大评价结果的差异性，更好地体现综合性和定量性，减少不确定性。

3 基于BP神经网络的砂砾岩储层质量评价

研究区砂砾岩储层非均质性强，需要借助多方面、多角度评价参数进行表征来实现储层质量的定量评价，但储层质量评价参数之间关系复杂，相互间多呈非线性关系，并且复杂的关系与最终结果的准确度相对立［20］，想要通过常规方法得到储层质量综合评价指数更为困难。现代兴起的人工神经网络技术可通过自身机器学习，较为智能地解决上述复杂问题［21-23］。文中通过采用BP神经网络模型解决关系复杂的非线性问题，较好地实现研究区砂砾岩储层质量的定量评价。

3.1 BP神经网络模型简介

BP神经网络模型是目前人工神经网络方法中应用最为广泛的神经网络模型，属于多层前向型网络，由多个输入层、一个输出层和多个隐含层组成（图4a）。首先将训练数据加载至网络的输入层中，靠自身逐层训练至输出层，得到相应的“预估值”，再将“预估值”代入交叉熵损失函数中计算误差，然后通过机器不断学习并利用误差反向传播训练算法，反向从输出层对连接权值进行修改，并逐步后退至各层和节点，最后直至隐含层，通过持续迭代修正连接权值和阈值，确保均方根误差控制在相应的误差精度范围内，最终建立多元输入数据与单元输出数据之间非线性映射关系，从而得到期望结果，完成网络学习（图4b）。

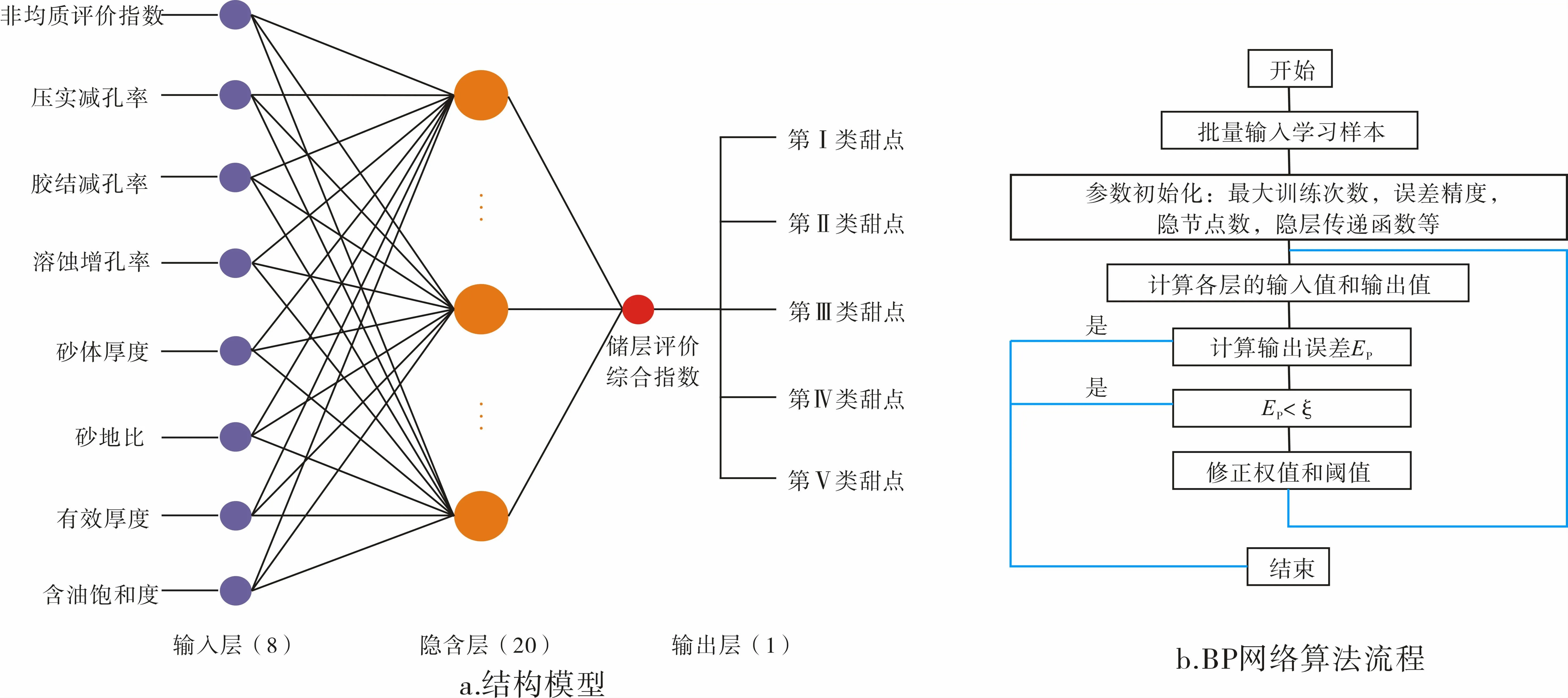
图4 BP结构模型及网络算法流程

3.2 BP神经网络建模及应用

3.2.1 储层质量评价参数优选探讨

储层质量是储层储集和渗流能力的表达［24-25］，储层质量评价选择的参数最好是相互独立的、属性意义明确的，尽可能评价储层的各个方面。文中选择的储层质量评价指标包括非均质性评价指数、成岩相（压实减孔率、胶结减孔率、溶蚀増孔率）、砂体厚度、砂地比。有些学者会使用比较新的评价指标，例如基于压汞、核磁实验等得到的排驱压力、孔喉半径、饱和度、阈压梯度等微观机理分析指标［26-27］，但这些指标实际受限较大，并不能有效指导宏观储层评价。

3.2.2 构造输入层和输出层

储层质量评价指标的输入层为非均质性评价指数、压实减孔率、胶结减孔率、溶蚀増孔率、砂体厚度和砂地比；输出层根据生产情况划分为五类储层，分别以指标值0.8～1.0、0.6～0.8、0.4～0.6、0.2～0.4、0～0.2进行划分。

3.2.3 建立BP神经网络结构

采用三层网络结构，输入层节点为6（6个评价指标），输出层节点为1（储层评价综合指数）；根据经验，将隐含层节点设为20，建立研究区砂砾岩储层类型的BP神经网络结构模型（图4a）。

3.2.4 深度神经网络模型训练

将沙四上亚段7砂组和8砂组中的174个样本点作为训练数据（占总样本数的80%），用于机器学习训练；22个样本点作为检验样本（占总样本数的10%），用于验证学习结果的准确性；22个样本点作为测试样本（占总样本数的10%），用于机器预测储层类型。

3.2.5 BP神经网络模型结果分析

BP神经网络采用三层网络结构，网络最大训练次数设为1 000，误差精度为1×10-4。当网络系统误差小于给定的误差时训练结束，训练共进行16步，在第10步时效果最佳，均方差最小为0.000 579 94（图5）。

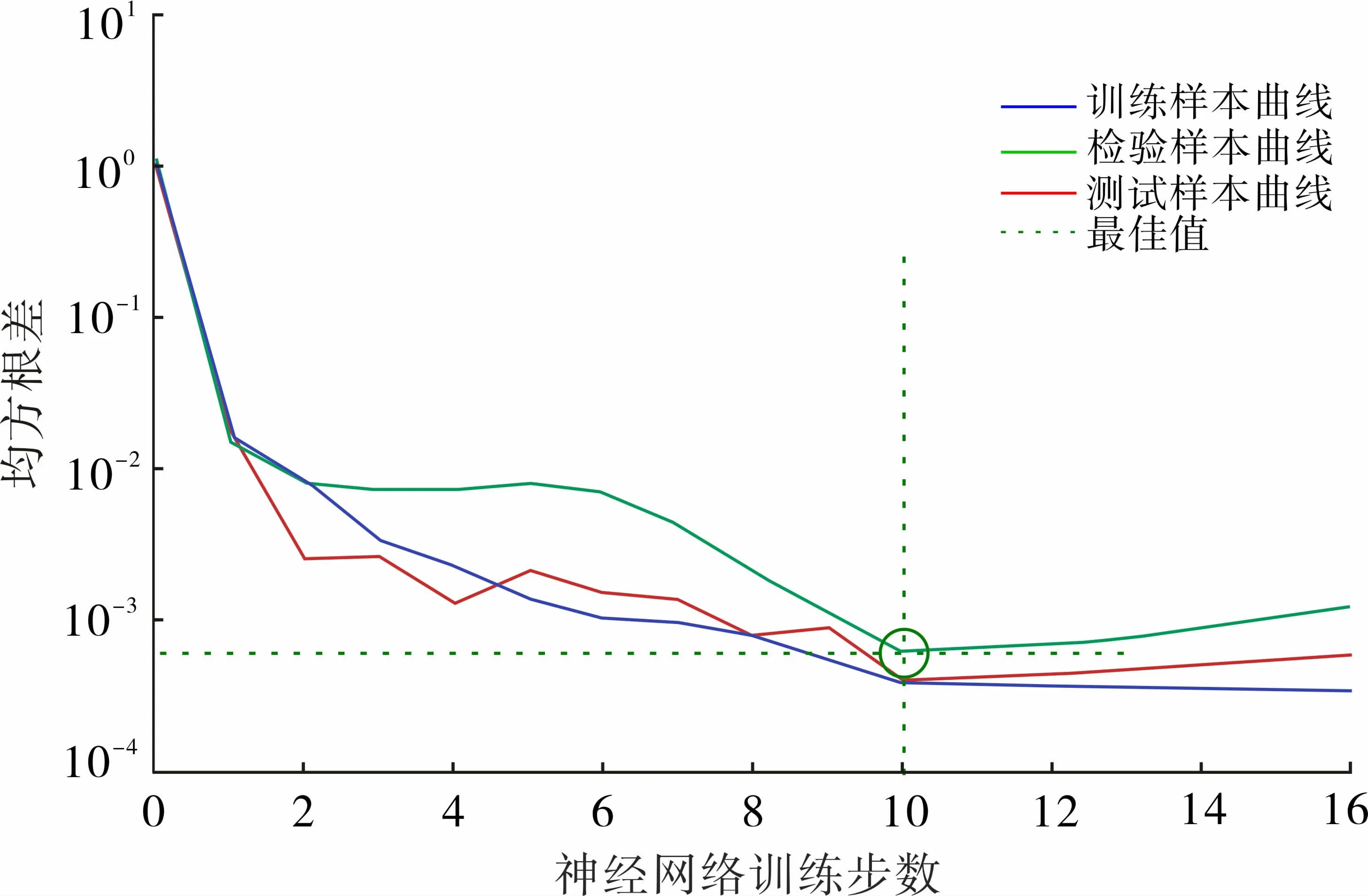
图5 BP神经网络的训练误差传播曲线

由图6可知，三条拟合曲线的相关系数均大于0.90，从训练至测试效果都能达到很好的拟合并反向对人工解释进行指导，本次机器学习的识别结果准确度较高，得到的结果即为预期想要得到的结果。

图6 BP神经网络的训练、检验、测试拟合曲线

通过机器识别结果和人工解释结果相比较，发现BP神经网络模型的预测类型与实际人工划分的储层类型基本一致，用其对22个测试样本进行预测，预测结果中有20个结果识别正确，预测储层类型的准确率大于90.09%（表2）。相反，人工进行储层分类时有时并不十分精确，且花费的时间成本较高。因此，深度神经网络模型的预测结果可提供快速有效的参考。

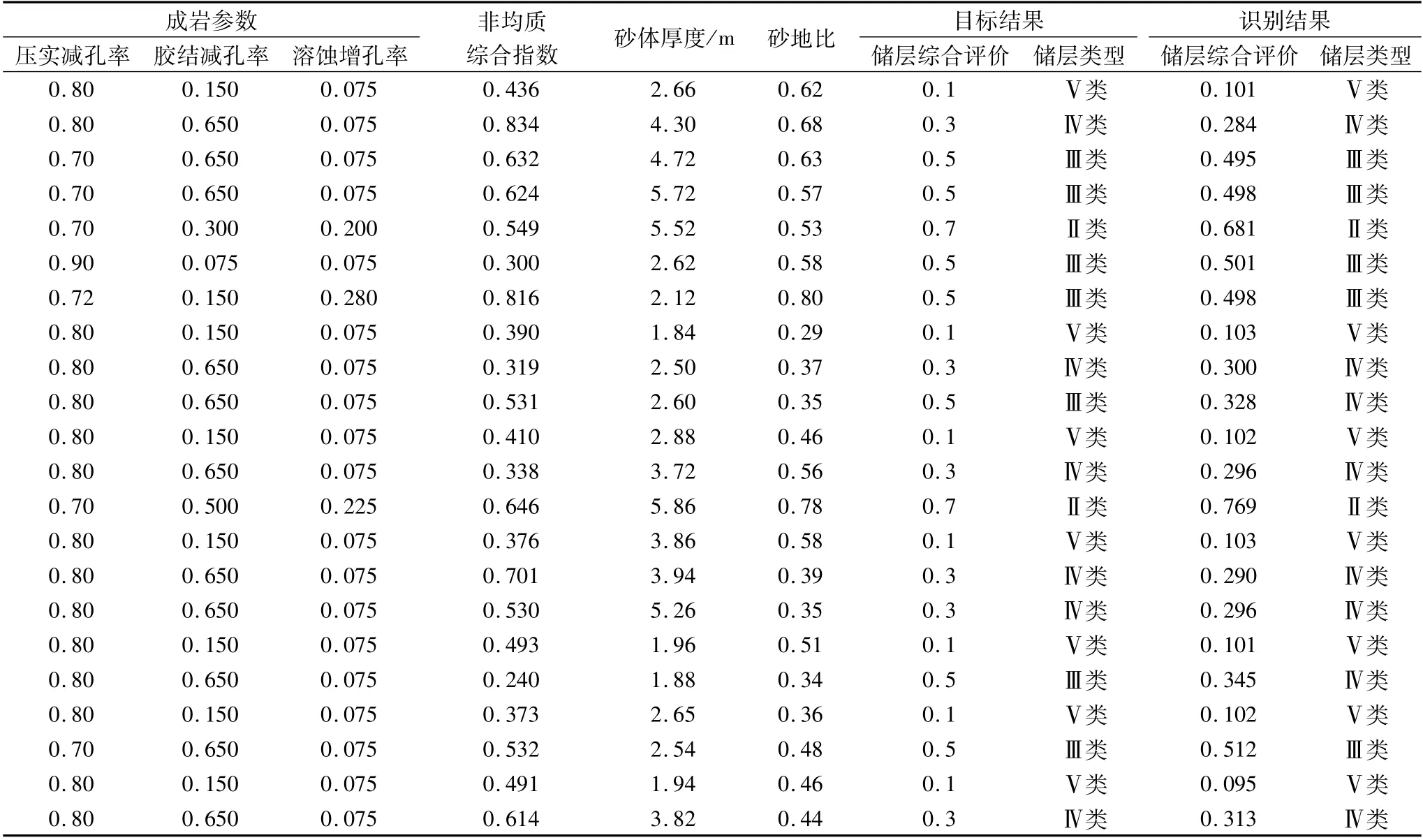
表2 LA区块目的层砂砾岩储层类型识别结果

3.3 储层质量评价

通过从各角度选择多评价参数对研究区砂砾岩储层质量评价，储层类型可分为五类：Ⅰ（好）、Ⅱ（较好）、Ⅲ（中等）、Ⅳ（较差）、Ⅴ（差）。其中Ⅰ类储层指标值为0.8～1.0，Ⅱ类储层指标值为0.6～0.8，Ⅲ类储层指标值为0.4～0.6，Ⅳ类储层指标值为0.2～0.4，Ⅴ类储层指标值为0～0.2。

通过对各类储层与其对应的单井地质特征进行比较，认为实践结果与单井地质认识具有良好的匹配关系。研究区目的层以Ⅱ类和Ⅲ类储层居多，Ⅰ类和Ⅱ类储层岩性多以中-粗砂岩、含砾砂岩、细砾岩为主，对应沉积微相为沟道和辫状水道，物性较好，含油性较好，可作地质甜点（图7a，7b）；Ⅲ类储层岩性以中-粗砂岩为主，发育辫状水道，但物性中等，含油性一般（图7c）；Ⅳ类储层以粉细砂岩为主，对应扇中前缘沉积，物性较差，含油性多显示荧光（图7d）；Ⅴ类储层几乎不含油，对实际开发作用不大，因此这里不考虑（图8）。

图7 LA区块沙四上亚段各类储层对应单井地质特征

3.4 评价结果的应用

以L2井为例，储层质量评价结果与实际地质认识相吻合（图8a）。综合单井主力层储层评价结果和以其结果作为目标属性进行反演得到的储层评价数据体，预测储层类型在平面上的展布（图8b、8c）。由储层定量评价平面分布图可以看出，整体上储层类型区分明显，储层展布较为精细，类型较好的储层在平面上多呈条带状，较为贴近河道主体沉积。综上所述，评价成果可较好地划分储层类型，为砂砾岩储层质量评价及优势储层预测提供较好的应用前景，也为其他地区砂砾岩储层质量评价提供参考。

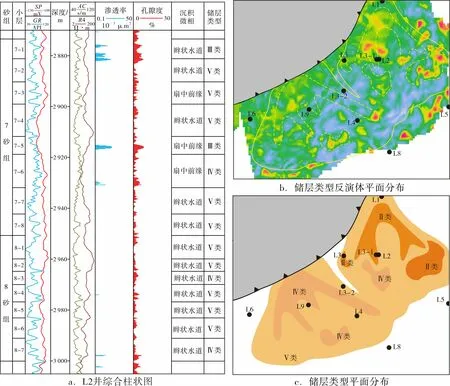
图8 L2井7、8砂组储层综合柱状图及储层评价（8-3小层）

4 结论

（1）综合利用熵权法与模糊层次分析法，构建熵权、模糊互补判别矩阵，有效扩大评价结果的差异性，从而得到储层层间非均质性评价指数，能够更好地克服传统方法各参数表征角度各异、评价指标无边界、各参数评价结果相互矛盾等问题，更好地体现综合性和定量性，减少不确定性。

（2）基于BP神经网络方法将LA区块沙四上亚段砂砾岩储层划分为五种类型，研究区以Ⅱ类和Ⅲ类储层发育为主，Ⅰ类和Ⅱ类储层可作为有利的地质甜点。最终预测储层类型平面展布，储层类型较好的平面上多呈条带状，较为贴近河道主体沉积，分 类结果与实际地质认识相吻合。