轴向打孔装药爆炸切断TC4钛合金板的研究❋
2022-06-10何志杰
朱 宇 王 猛 何志杰 赵 康 秦 雨 陈 刚
安徽理工大学化工学院(安徽淮南,232000)
引言
伴随着航空发动机技术水平的不断提升,叶片旋转速度进一步加快。由于涡轮扇叶受到离心作用、热负荷及振动载荷等多重因素影响,容易在运行过程中失效,进而发生航空发动机不包容事故;处于高速、高能状态下的碎片极其可能击穿机匣,导致机毁人亡的重大灾难。因而,研究航空发动机机匣的包容性具有重大意义。
包容性试验可验证机匣是否能够承受高速飞溅的碎片[1],要求钛合金叶片在特定方位及特定转速时发生断裂,并且不会产生超高速破片,通常采取爆炸分离的方法。目前,对爆炸分离的研究主要集中于尖端领域的火工分离装置及航空发动机叶片分离。武新峰等[2]运用ANSYS/LS-DYNA创建了一种卫星火箭连接结构的计算方式,并通过试验验证了包带的相关参数会对星箭分离过程产生巨大影响。胡坤伦等[3]采用量纲分析法,结合几何相似率,经过数值模拟和试验对比,得到了钛合金板的最小壁厚、装药直径和缓冲层厚度之间的最佳比例关系。Takeuchi等[4]通过模拟航天器断裂分离的过程,判断了相应的冲击响应。Ramesh等[5]利用ANSYS对不同材料的发动机进风扇叶片的变形特性进行了研究。Barlow等[6]进行了飞机发动机风扇叶片附件中的疲劳裂纹传播模拟。何志杰等[7]采用AUTODYN软件探究了无约束状态下和两种不同材料约束下导爆索爆炸分离复材板的情况。
对于TC4钛合金板的爆炸分离问题,多数情况下选取聚能切割法。聚能装药工艺结构复杂,操作难度系数较高,且装药量大。故参考工程爆破中分散布药的方法,设计了沿轴向打单孔和双孔两种新式装药结构,运用AUTODYN仿真软件中的SPH算法对TC4钛合金板的断裂过程进行数值仿真,并结合试验结果比较两种装药结构的优劣。
1 数值模拟
考虑到钛合金板在爆炸分离时会出现极大的变形和大量飞散的碎片,选用AUTODYN中一种无网格的SPH计算方法[8-9]来确保计算过程的稳定性。
1.1 算法介绍
SPH算法中,光滑长度h是每个粒子参加运算时确定与其发生关系的邻域空间步长,决定着计算精度和计算效率。h取值过小,不能对质点提供足够的作用力,从而降低计算精度;h取值过大,则质点的详细特征和局部性质可能会被消除,同样会降低精度。为使SPH方法精确可靠,Benz等提出了光滑长度h与密度ρ相关的指数形式[10]:
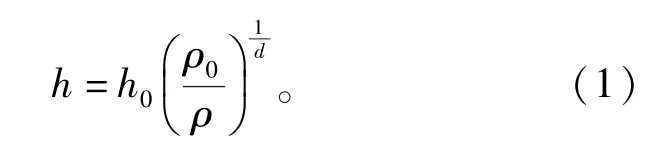
式中:h0和ρ0为初始光滑长度和初始密度;d为空间维数。
基于SPH的离散化流体动力学方程有[11]:
质量守恒方程

动量守恒方程
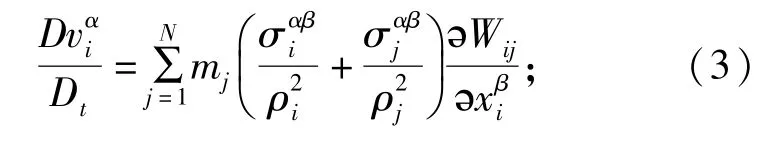
能量守恒方程
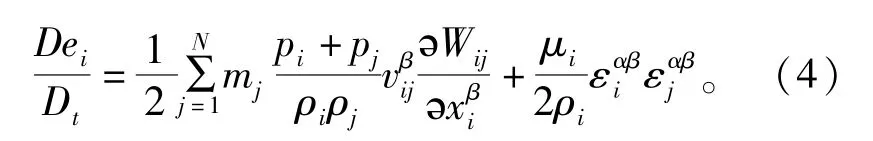
式中:v为速度;e为热能;σ为应力张量;p为压力;m为质量;ρ为密度;μ为动力黏滞系数;ε为动剪应变率;N为质点总数;x为坐标轴符号;α、β代表不同坐标轴;i为计算质点记号;j为邻近质点记号;W为核函数。
1.2 方案设计
TC4钛合金板尺寸为100 mm×80 mm×23 mm。拟采用轴向双孔(方案I)和轴向单孔(方案II)两种装药方式进行切断,模型如图1所示。单孔方案中,炮孔直径为10 mm;双孔方案中,取1/2板材的几何中心作为炮孔圆心,每个炮孔直径为5 mm。药柱长度均为100 mm。根据数值模拟的结果择优选择方案,对炮孔直径进行调整。
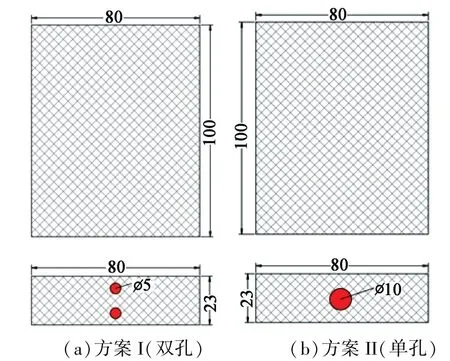
图1 模型几何尺寸(单位:mm)Fig.1 Model geometry(Unit:mm)
1.3 仿真模型
炸药为钝化的RDX,采用JWL状态方程[10,12]。
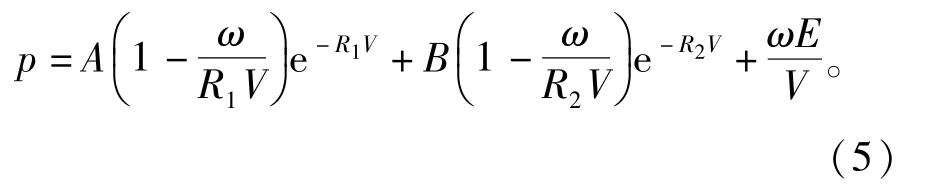
式中:p是爆轰产物的压力;E为单位体积热力学能;V为相对体积;A、B、R1、R2、ω为常数。
钝化RDX的JWL状态方程参数见表1。

表1 钝化RDX的JWL状态方程参数Tab.1 Parameters of JWL state equation of passivated RDX
TC4钛合金板采用大应变率的Johnson-Cook模型来更新偏应力。忽略温度的影响,由于材料静水压力远大于屈服应力,固体材料表现出可压缩流体的特性,所以需采用Mie-Gruneisen状态方程来求解压力项。TC4钛合金板的材料参数如表2所示。表2中,Cg为材料有关的系数;S为常数。

表2 TC4钛合金板的材料参数[13]Tab.2 Material parameters of TC4 titanium alloy plate
采用AUTODYN软件建立有限元模型。两种方案中,水平方向均为X轴方向,竖直方向均为Z轴方向,粒子间距均设为0.5 mm。单孔方案中,TC4钛合金板和炸药共有1 472 000个粒子;双孔方案中,共有1 440 000个粒子。药柱中心设为起爆点,并沿钛合金板表面Y轴中轴线上每隔25 mm设置1个测点,用于了解钛合金板的性能变化情况,计算模型如图2所示。

图2 计算模型及测点Fig.2 Calculation models and measuring points
2 计算结果与分析
2.1 计算结果
两种切断方案的计算结果如图3所示。由图3(b)可以直观地看出,钛合金板仅在靠近起爆点附近产生的爆炸效应明显,板材隆起较高,粒子飞散严重,远离起爆点一端的材料有被拉开的现象。而图3(a)中可以清楚地观察到,钛合金板接近于恰好切断,形状规整。

图3 方案I和方案II的模型计算结果Fig.3 Calculation results of Scheme I and Scheme II
为了进一步探究装药直径对爆炸切断结果的影响,对装药直径进行细微的调整。增加两组模拟方案,设为方案III和方案IV,装药直径分别为双孔∅4 mm和单孔∅8 mm,其余参数不变。模型计算结果见图4。从图4(a)看出,方案III中,TC4钛合金板仅在中轴线上略微突起,并未断开;而图4(b)中,TC4钛合金板已经完全被切断,并产生大量飞散的破片,板材损伤严重。结合4种方案计算结果可知,双孔装药的方式更加适用于钛合金板的爆炸切断。

图4 方案III和方案IV的模型计算结果Fig.4 Calculation results of Scheme III and Scheme IV
2.2 装药参数分析
表3是4组仿真的装药参数及模拟结果。装药直径的大小直接影响了装药量的多少,从而影响爆炸切断的能力。从表3中能够看出,将单孔装药直径减小一半并分成两个孔进行装药,不仅可以减少药量、节约成本,还达到了更好的爆炸切断效果。

表3 模型装药参数及模拟结果Tab.3 Charge parameters and simulationresults of models
测量分离成两块的钛合金板两侧断裂纹路的最大间距来判断板材受损情况。图5为I、II、IV 3种方案计算测得的3组最大间距对比。由图5可以看出,采用单孔装药结构时,随着装药直径的增加,板材间最大损伤间距几乎呈线性增长。也就是说,板材受损情况受孔径大小影响,装药直径越大,钛合金板受损越严重。相对于单孔装药来说,双孔装药对板材造成的损伤更小,且效果更好。
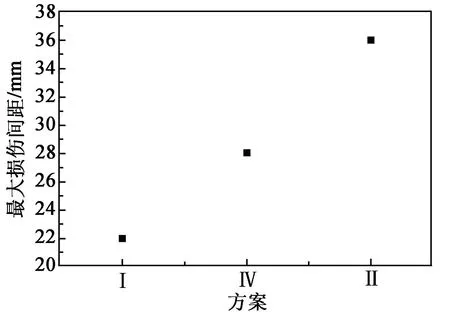
图5 不同方案得到的最大损伤间距Fig.5 Maximum damage spacing obtained by different schemes
2.3 Mises应力分析
Mises屈服准则[14]认为,材料产生屈服是由于畸变能密度引起的。炸药爆轰时会产生剧烈的冲击压缩波。当压缩波传到钛合金板表面时,钛合金板受到冲击压缩,随即发生反射,并产生稀疏波。在反射冲击波的作用下,钛合金板发生拉伸断裂。观察各测点的Mises应力,并结合Mises屈服准则来推断材料是否发生断裂。
Mises屈服准则应力分量与等效应力表达式[15]:
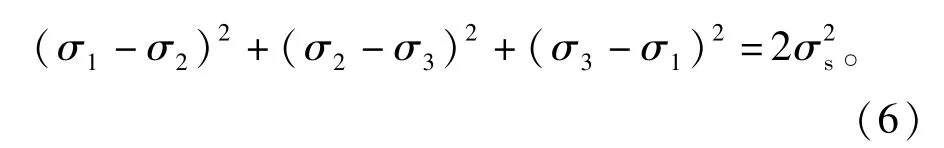
式中:σ1、σ2、σ3分别表示X、Y、Z方向的主应力;σs表示等效应力。
分别取4组方案模型的测点1#、3#和5#,观察各方向的应力和Mises应力峰值,并根据式(6)计算其等效应力,如表4所示。参照Mises失效理论,当Mises应力σ>σs时,测点附近的材料发生屈服。选取方案I和方案III中测点1#~5#绘制Mises应力和等效应力关系图,如图6所示。

图6 各测点Mises应力和等效应力的关系Fig.6 Relationship between Mises stress and equivalent stress at each measuring point
结合表4和图6可以明显看出:方案I、II、IV中各测点的Mises应力先增大后减小,呈二次函数分布。并且方案I、II、IV的Mises应力均大于其等效应力;而方案III的结果恰好相反。根据Mises失效理论可以初步推断,采用∅4 mm双孔装药方案未能使钛合金板产生断裂。分析原因,是由于4 mm孔径的装药量较小,炸药爆轰时会因材料自身和外界等因素造成能量的耗散,剩余能量不足以破坏板材,而其余3种方案均可用来切断钛合金板。

表4 各方案模型的测点处应力Tab.4 Stress at the measuring points of each model GPa
2.4 速度与加速度分析
图7为分别采用∅5 mm和∅4 mm双孔装药方式时测点5#的速度变化曲线。如图7(a)所示,炸药爆炸瞬间,钛合金板受冲击压缩,测点5#的速度瞬间增加至1 485 m/s;当冲击波传播到钛合金板的表面后,会反射一稀疏波,钛合金板继续膨胀,测点5#的速度迅速增加至1 883 m/s。由于受到附近物质质点的约束,测点速度下降至1 600 m/s,此时又在高温、高压爆轰气体的作用下,测点5#的速度再次增长。但是,爆轰气体的膨胀相对于冲击波的传播是一个相对缓慢的过程,因此,速度增长相对缓慢。从图7(b)中可以看出,测点5#的速度瞬间达到最大值;随后,在前、后反射稀疏波和压缩波的相互作用下,速度一直上下波动;因波在传播过程中不断衰减,且同时受到附近的物质质点的约束作用,故而速度在零点附近振荡,最后逐渐趋近于0。由此,可以判断出测点5#处并未发生断裂。

图7 双孔装药结构测点5#的速度变化Fig.7 Velocity variation of measuring point 5#in double-hole charge structure
图8给出了采用∅5 mm双孔装药结构下各测点加速度a的变化情况。从图8中能够得知:测点1#~2#前期在爆炸冲击作用下,加速度产生剧烈振荡,并在短时间内发生衰减,进入低频振荡阶段;测点3#的加速度前、中、后期均出现反复振荡,这是由于应力波在板材内向前传播,与前时刻的反射稀疏波交汇,在应力波的来回反射下造成反复波动;在测点4#~5#形成的反射拉伸波沿各自相反方向传播,并对板材造成拉伸效应。
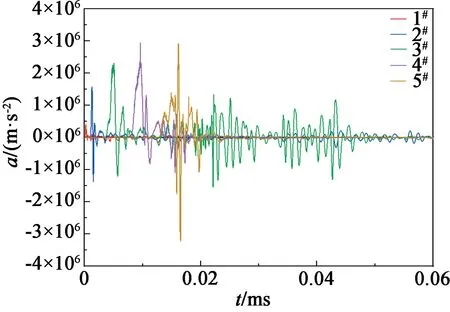
图8 ∅5 mm双孔装药结构各测点的加速度变化情况Fig.8 Accelerated velocity variation of each measuring point in∅5 mm double-hole charge structure
3 钛合金板切断试验
3.1 试验设计
依据表3中的仿真方案设计4组对应的试验,打孔如图9所示。

图9 两种装药试验方案Fig.9 Two charging test schemes
单孔和双孔装药结构均将一端开孔处用绝缘胶带密封,从另一端采用钝化RDX进行装填。剪取适当长度的导爆索,安放在未密封端的端口,一个孔安放一根导爆索,并将导爆索的末端与一根导爆管雷管用胶带捆绑连接。为了确保起爆以及传爆的稳定性,必须使导爆索的弯折程度小于90°,且保证导爆索与填装的钝化RDX紧密接触。具体连接方式如图10所示。

图10 两种起爆连接方式Fig.10 Two initiation connection modes
3.2 试验结果及分析
收集4组板材的试验结果进行对比,如图11所示。从板材试验切断效果可以看出,采取∅10 mm单孔装药的II号板和∅8 mm单孔装药的IV号板均被完全切断,板材受损严重,板材断裂处裂纹形状不规则;∅5 mm双孔的I号板断裂纹路清晰整齐,板材受损较小;仅采用∅4 mm双孔装药的III号板未被切断。II号板和IV号板由于装药量较大,爆炸作用的能力强,炸药爆炸形成的冲击波以球面波的形式向外扩张,在遇到自由面时又被反射回稀疏波,板材在反射拉伸作用下产生破坏效应,由于能量过大,导致剩余能量仍有部分会作用于板材四周,从而促使板材损伤进一步增大;III号板的孔径和装药量最小,板材在中部略微隆起,并在炮孔端产生细小的裂纹,这是由于炸药爆炸产生的冲击波在钛合金板内向表面传播,发生了Hopkinson效应,对打孔处的介质产生拉伸作用,从而导致细微裂纹的产生。

图11 4组板材试验结果Fig.11 Test results of four groups of plates
为了进一步验证仿真模拟的准确性,图12给出了最大损伤间距的模拟与试验结果对比。能够看出,模拟与试验之间的误差仅在1~2 mm左右。这是由于仿真模拟是在理想条件下进行的,忽略了一些不确定因素;而试验过程中,由于机械加工造成孔径大小存在误差,从而导致装药量不准;再加上外界环境等其他因素的影响,难免与模拟结果有些差距。并且随着孔径的增加,模拟结果与试验结果的误差在变大。
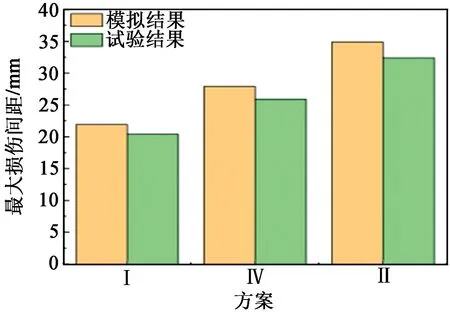
图12 模拟与试验结果对比Fig.12 Comparison between simulation and test results
4 结论
设计了用于爆炸切断TC4钛合金板的轴向单孔和轴向双孔两种装药结构。通过数值模拟和试验,探究了两种装药结构的优劣性,并通过调整孔径,找到了最佳切断方案,模拟结果和试验结果高度一致。得到以下结论:
1)双孔装药结构明显优于单孔装药结构,可以在降低装药量的同时,提升爆炸切断的效果。
2)细微调整孔径后发现,调整孔径大小能够改变爆炸切断的效果,爆炸切断能力会随着孔径的增大而增强,且钛合金板的损伤也随之增大。
由于各方面因素,仅仅探究了轴向单、双孔装药的优劣性,得出双孔装药比单孔装药更优。可进一步提高精度进行双孔切断研究,找寻切断板材的临界装药直径。
