基于爬坡特征和云模型的风电功率预测误差区间评估

乔妍，韩 丽，李梦洁

（中国矿业大学电气与动力工程学院，江苏省徐州市 221116）

0 引言

当前世界各国面对化石能源日渐枯竭的情况，都将研究重心转移到风能等可再生能源的开发和利用上。虽然风力发电具有能够改善生态环境等优点，但风电的不确定性对于电力系统的安全稳定运行而言也是一个巨大的难题。而提前得到准确的风电功率预测结果，就能在了解发电规律的情况下进行电网调度，不仅能够提高电力系统的安全稳定性，还能降低运行成本［1-2］。国内外已有的研究大多为传统的确定性风电功率预测方法，得到的是未来某一时刻下可能出现的确切风电功率值。常见的方法有自回归滑动平均模型［3］、人工神经网络法［4］、支持向量机法［5］等。虽有较好的预测效果，但确定性预测方法始终无法全面地描述风电规律，无法对风电功率不确定性做出定量描述，即无法估计风电功率可能出现的波动范围［6］。因此，为了满足电网的运行和调度要求，有必要对能够得到风电功率波动范围的概率预测进行预测研究。

概率预测基于不同输出形式可分为概率密度预测、分位数预测和区间评估。对于风电功率区间评估而言，目前常见的评估方法有:利用Beta 分布［7］、Logistic 分布［8］、混合Gaussian 分布［9］等分布模型拟合误差的参数型方法，以及利用分位数回归模型［10］、核密度估计［11］等非参数型方法。文献［12］在此基础上提出了基于动态云模型的短期风电功率区间评估方法，但风电功率预测误差在短时间内急剧变化的情况下，即发生风电爬坡事件时，更易产生实际功率超过评估区间范围的结果。这是由于风电爬坡事件属于小概率突发性事件，现有研究中的模型通常难以挖掘其规律。文献［13］通过数值天气预报风速和蒙特卡洛法得到了较好的区间评估结果，但该模型在风电功率变化剧烈的时段误差较大，这是由于爬坡事件中风电具有更为强烈的随机性和波动性，导致该时段的评估精度降低。由于爬坡事件发生时风电功率的非线性远远高于非爬坡时段，且预测误差相较于非爬坡段而言数值普遍更大，文献［14］提出了一种考虑爬坡特性的风电功率区间评估方法，通过二维核密度估计和小波神经网络挖掘爬坡特性对预测时刻误差的影响，但模型中未考虑到不同的爬坡特征类型下的预测误差所具有的不同分布规律。

因此，本文提出了一种基于风电爬坡特征建立云模型的误差区间评估方法。为了充分考虑爬坡特性对误差评估的影响，首先，利用改进的旋转门算法（optimal swinging door algorithm，OpSDA）识别爬坡后得到的爬坡特征，并基于爬坡特征对预测误差进行分类。为了研究不同类别误差的分布特性，掌握误差数据的特点以得到更为精确的区间评估结果，对上爬坡类误差和下爬坡类误差分别建立云模型，对非爬坡类误差采用K-means 算法，得到了3 类误差区间范围。最后，为了挖掘数据特征，以风电功率和爬坡特性为模型输入，误差类型为模型输出，建立误差评估模型学习数据间的非线性映射关系。

1 基于爬坡特征分类的云模型

1.1 云模型基本原理

云模型是用于处理某个定性概念与其定量描述的不确定转换模型［15-16］。由于其能反映出数据的随机性，而风电具有强随机性和波动性，所以近年来被广泛应用于风电功率预测、风速预测等领域［17-18］。

假设存在集合Q={c}，其中Q 为定值c 的论域。对于论域Q 中的模糊集合而言，集合中任意元素c 都存在一个有稳定倾向的随机数，称为c对的隶属度。论域Q 上的分布被称为云，元素c 的定值被称为云滴。云模型的拟合公式［19］为:

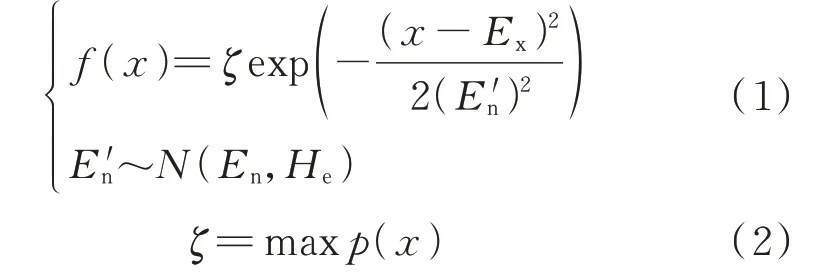
式中:f(x)表示云模型的概率分布；Ex为云模型期望值参数；En为云模型熵值参数；为随机数；He为云模型超熵参数；ζ为拟合修正量；p(x)为变量x概率分布曲线的峰值概率。

根据拟合公式得到典型的云模型分布如附录A图A1 所示，云模型通过期望Ex、熵值En、超熵He这3 个特征参数表征云滴的分布特性。

对于本文研究的风电区间评估而言，云滴即为风电功率预测误差。期望Ex指预测误差在论域分布中的期望，是最能够代表定性概念的点，一般采用样本的均值。熵值En由定性概念的随机性和模糊性共同决定，能够表示预测误差的不确定性程度，即能表示出误差的幅值波动范围。超熵He是熵值En的不确定性量度，超熵越大，云的离散程度越大，隶属度的随机性也随之增大，云的厚度也越大，能够表示出预测误差的集中程度。其计算公式如下:

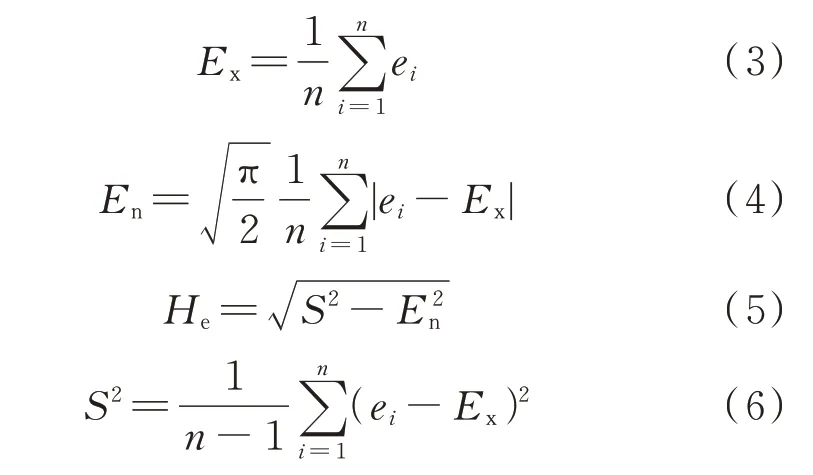
式中:i为样本序号；n为样本总数；ei为风电功率预测误差；S2为样本方差。

云模型根据计算过程不同分为正向云变换与逆向云变换。

1）正向云变换是指基于定性概念的3 种参数特征而生成云滴，通过式（7），以期望Ex、熵值En、超熵He这3 个特征参数量化风电功率预测误差的波动幅值、波动范围及波动离散性。

式中:randn(1)表示服从均值为0、方差为1 的正态分布。

2）逆向云变换是指基于一些给定的云滴（即风电功率预测误差训练样本），求出符合该云滴样本分布规律的3 个特征参数。

对整体风电预测误差数据建立的传统云模型难以完全体现风电数据的不确定性，难以在不同误差类型下时刻展现较高的可靠性和普适性。因此，本文首先通过爬坡识别算法对样本数据进行分类，再结合正向云变换和逆向云变换，建立基于爬坡特征分类的云模型。从定性到定量的角度进行风电功率误差区间评估，可以提高各种风电数据类型下评估结果的可靠性。

1.2 基于爬坡特征分类的云模型建立

由于风电功率点预测误差是必然存在且无可避免的，所以对于电力系统规划和运行而言，能够得到误差区间评估范围的风电功率不确定性预测，是解决高比例风电经济、安全消纳的关键技术。而挖掘出风电功率点预测误差数据的特点则是得到良好风电功率区间评估结果的前提。风电爬坡事件是指风电功率在短时间内发生单向大幅变化的现象，由于该种现象在风电序列中属于小样本事件且变化幅值较大，因此加大了预测难度，致使爬坡事件发生时风电功率点预测会存在较大误差［20］。

根据文献［11］，风电爬坡事件被定义为当t至t+Δt时段的首末时刻功率之差的绝对值超过给定阈值时的事件。

式中:Pt+Δt为t+Δt时刻的功率；Pt为t时刻的功率；Pthreshold为给定阈值。

根据参考文献［21］，本文设定Pthreshold为额定装机容量的3%。根据爬坡方向的不同，爬坡事件可以分为上爬坡事件和下爬坡事件，上爬坡事件是指一段时间内风电功率骤增（Pt+Δt-Pt＞0），下爬坡事件是指一段时间内风电功率骤减（Pt+Δt-Pt＜0）。

基于对风电爬坡事件的性能分析，定义爬坡事件的4 个重要特征如附录A 图A2 所示，分别为:爬坡率RR、爬坡幅值RSW、开始时间RST和持续时间RD。

因此，风电功率序列数据可以根据是否发生爬坡事件以及发生哪一类爬坡事件进行分类。本文基于文献［22］，利用OpSDA 对爬坡事件进行识别，并基于爬坡特征将风电数据分为3 类，分别为上爬坡类、下爬坡类、非爬坡类。OpSDA 首先通过传统的旋转门算法（SDA）得到风电功率爬坡的初始分段点，将初始分段点作为时间端点在任意一段风电功率时间序列上建立目标函数，根据由爬坡定义设定的爬坡准则建立记分函数并作为约束条件，通过求取目标函数的最大值以识别风电爬坡事件。

以Elia 公司某比利时风电场2019 年4 月4 日05:30 至4 月6 日02:00 的风电功率数据为例，利用OpSDA 识别的爬坡分类曲线图如附录A 图A3 所示。根据图A3 可知，该时间段内分别有4 个非爬坡事件（蓝色曲线段）、3 个下爬坡事件（黄色曲线段）和3 个上爬坡事件（红色曲线段）。改进后的算法根据传统的SDA 分段点将相邻且爬坡方向相同的事件划分为同一事件。根据时间轴顺序，在第1 个上爬坡事件（第1 个红色曲线段）中就存在变化幅值小却与邻近爬坡变化方向相反的事件，它与邻近大幅值爬坡共同组成第1 个爬坡事件，改善了传统的SDA 不能识别长时段爬坡的缺点。

对3 种误差数据分别建立云模型，根据3 类云模型得到3 个误差评估区间。由于风电功率的强随机性，使得在基于点预测模型得到预测误差时，由OpSDA 识别出的非爬坡段也可能存在少量较大误差的情况。而基于文献［23］，K-means 算法基于欧氏距离这一指标对风电预测误差进行分类，使误差数值相近的点被归为一类，能够缩小评估范围，避免评估精度被识别为非爬坡类事件中少量大误差影响。而且对于电网的经济调度而言，误差评估区间的宽度越窄，需要的备用裕量越少。为了进一步减小误差评估区间的宽度，利用K-means 算法将非爬坡类误差的绝对值根据数值大小再分为2 类，分别为大误差类和小误差类，将小误差类的误差评估区间取代基于云模型所得的误差评估区间作为该类的误差评估区间。

2 基于爬坡分类的预测误差区间评估

2.1 评估模型设计

为了能够有效学习到具有强随机波动性的风电数据及误差特征与小样本爬坡事件的时序相关性，并得到针对风电爬坡事件具有良好区间评估效果的结果，采用近年来被广泛用于风电预测领域的神经网络模型［24-26］建立预测误差评估模型对误差类别数据进行训练和学习。

由于预测误差的分布情况与爬坡事件的特征和风电功率的自身波动相关，因此，本文建立的误差评估模型改变了输入输出数据类型，以研究误差特征与风电爬坡事件之间的相关性。将风电功率和爬坡特征（爬坡率、爬坡幅值、开始时间和持续时间）共同作为评估模型输入，使模型在训练学习过程中能够同时兼顾风电功率时间序列的原始波动情况、风电爬坡事件的特征规律以及不同类别爬坡所具有的不同误差分布情况。将误差类别作为评估模型的输出，即模型可以由功率和爬坡特征直接得到误差类别，继而根据误差类别得到由相应云模型所得的误差评估区间范围。评估模型的表达式为:

式中:ht+a为预测误差类型，分别为（1，0，0）（上爬坡类）、（0，1，0）（下爬坡类）和（0，0，1）（非爬坡类）；xt，xt-1，…，xt-n为输入数据，输入数据xj由j时刻的风电功率数据Pj和爬坡特征数据RRj、RSWj、RSTj、RDj组合而成，即xj=(Pj，RRj，RSWj，RSTj，RDj)，j=t，t-1，…，t-n；a为超前预测步数，本文研究的预测误差区间评估主要为超前1 步（提前15 min）和超前16 步（提前4 h）的超短期预测，分别为a=1和a=16。

本文之所以采用神经网络建立评估模型，是由于神经网络能够充分逼近由风电爬坡强随机性导致的风电功率、爬坡特征与预测误差之间十分复杂的非线性映射关系。通过确定性预测模型学习到不同爬坡类型预测误差的分布特性，由实际风电功率值和其对应的爬坡特征直接评估得到误差类型，继而得到评估误差区间，通过叠加预测功率值得到区间评估结果。评估过程结合了不确定性模型对于误差概率密度分布的拟合和确定性模型对于爬坡和误差数据特征的挖掘，由功率和爬坡特征直接评估误差范围，有利于电力系统工作人员基于爬坡事件的评估区间范围做出更合理的决策，减小爬坡事件发生时造成发供电不平衡等现象的可能性。

2.2 评估模型建立的整体思路

本文为分析不同爬坡类型的预测误差特性，提出了一种基于风电爬坡特征和云模型的预测误差分类区间评估方法。区间评估方法的具体步骤如下:

1）利用OpSDA 识别历史实际风电功率数据，得到历史爬坡特征值R={RR，RSW，RST，RD}，并根据爬坡方向，将历史风电功率预测误差数据分为上爬坡、下爬坡、非爬坡3 类；

2）对3 类历史误差数据分别建模，其中对上爬坡和下爬坡2 类误差建立云模型，并基于误差云滴得到相应的置信水平为90%的评估误差区间；而非爬坡类误差在取绝对值后利用K-means 算法将其分为2 类，以其中的小误差类作为非爬坡类对应的评估误差区间；

3）以历史风电功率P及其对应的爬坡特征R作为评估模型的输入，以评估误差类别作为评估模型的输出，建立评估模型以学习误差类别特征与风电功率及爬坡事件的联系；

4）根据误差评估模型得出的误差类别结果，综合不同类型所对应的误差区间以及风电功率预测值得到最终的区间评估结果。

评估模型建立的整体思路如图1 所示。

图1 评估模型的整体思路Fig.1 Overall idea of estimation model

2.3 模型评价指标

评估区间[L，U]由区间上界U和区间下界L组成，即

式中:F为风电功率预测值；Uh和Lh分别为预测误差值的上限和下限，其值根据预测误差类型h的不同而不同。h为（1，0，0）（上爬坡类）和（0，1，0）（下爬坡类）时，Uh和Lh对应预测误差云模型置信水平为90%的预测误差上限和下限；h为（0，0，1）（非爬坡类）时，Uh和Lh对应K-means 算法小误差类的预测误差上限和下限。

基于文献［27］采用评估正确率、评估区间覆盖率、区间平均带宽这3 类评价指标验证误差评估模型的正确性。由于本文主要研究的是基于爬坡特征的误差区间评估，在此基础上增加了爬坡段评估区间覆盖率和爬坡段区间平均带宽2 类指标以评价爬坡段的模型性能。

1）评估正确率Acc

式中:km为0-1 变量，当原始误差类别和评估误差类别相同时，km为1，反之为0；m为评估样本序号；N为评估样本数。

2）评估区间覆盖率IPICP

式中:cm为0-1 变量，如果评估目标值落入评估区间内，cm为1，反之为0。评估区间覆盖率越大说明区间评估方法的可靠性更高。

3）区间平均带宽IPINAW

评估区间的区间宽度δ为区间上界U与区间下界L之差，即

式中:δm为第m个评估样本的评估区间宽度。

仅考虑评估区间覆盖率容易造成区间范围过大，不符合实际应用需求。综合区间平均带宽指标可以提供更具有决策价值的评估结果。

4）爬坡段评估区间覆盖率IRPICP

式中:r为评估样本中发生风电爬坡事件的个数。

5）爬坡段区间平均带宽IRPINAW

本文的评价指标具有以下特点:在保证爬坡段评估区间覆盖率IRPICP数值越大的情况下，爬坡段区间平均带宽IRPINAW数值越小，评估效果越优。IPICP和IPINAW同理，即在保证区间评估结果覆盖住实际风电功率之后，评估区间范围越窄，模型性能就越好。这是因为较高精度的评估区间覆盖率能为电力系统的安全稳定运行提供保障，而较小范围的区间平均带宽能提高电网运行的经济性，两者应同时兼顾。

3 算例分析

本文评估方法中OpSDA 识别爬坡、云模型、Kmeanss 算法，以及评估模型中的反向传播（BP）网络模型、Elman 网络模型部分均采用MATLAB R2019b 进行编译。评估模型的长短期记忆（LSTM）网络模型部分是基于Keras 深度学习框架建立的，采用Python 作为编程语言，编译环境为PyCharm Community Edition 2020，处理器为AMD Ryzen 74800H，RAM 为16 GB。

基于Elia 网站某比利时风电场的数据进行研究，时间间隔为15 min。算例选取2019 年10 月至2020 年9 月该网站的数据并以四季的形式划分，每个季节各1 000 个数据分别进行误差区间评估，前50%用做训练集，后50%用做测试集。

3.1 不同爬坡类型云模型结果分析

以Elia 网站某比利时风电场［28］2019 年10月的风电数据为例，基于OpSDA 识别的不同爬坡类别的特征参数如附录A 表A1 所示。表A1 中爬坡开始时间使用datenum 函数转换为数字格式表示，非爬坡类的爬坡特征均用零值补全。由于篇幅限制仅展示样本数据的前7 个事件的特征结果。

基于Elia 网站中的风电功率实际值，利用自回归（AR）、BP 神经网络2 个点预测模型通过超短期预测得到2 种风电功率预测值。结合Elia 网站中最近的预测（most recent forecast，MRF）直接得到的预测数据，分别与风电功率实际值作差得到了3 组风电功率预测误差，由OpSDA 识别误差爬坡类型后得到的分类结果。为了更好地说明不同类型的误差云滴分布的不同，对每类所对应的风电功率预测误差数据分别建立云模型，得到云模型特征参数如附录A 表A2 所示。以基于AR 模型预测的预测误差云滴图（如图2 所示）为例，基于BP 神经网络模型和MRF 的预测误差云滴图见附录A 图A4 和图A5。而在实际评估过程中，非爬坡类误差直接采用Kmeans 算法的小误差类范围作为预测误差区间评估的依据。

由附录A 表A2 可知，在不同误差数据来源下，基于爬坡分类的云模型参数特征基本都符合以下规律:1）上爬坡类的云模型期望为负值说明该类预测误差大多为负值，即下爬坡事件中风电功率预测值通常小于实际风电出力；而下爬坡类云模型的期望为正值，所以下爬坡事件中预测误差数据分布规律与上爬坡相反；非爬坡类云模型的期望更接近零值且绝对值较小，所以该类预测误差数值整体偏小。2）上爬坡类和下爬坡类的云模型的熵值较大，所以不确定度也更大，使得误差概率密度分布较非爬坡类而言更为分散，即误差波动范围较非爬坡类而言更大。但预测误差数据来源不同使得云模型的特征参数也有一定的差异。MRF 误差的3 类云模型期望均为正，且数值偏大，表明不论在哪种误差类别情况下，MRF 风电功率点预测方法的风电功率预测数值均大于实际风电出力。而MRF 误差云模型的上爬坡类和下爬坡类的熵值较大，即误差的概率密度分布较为分散，非爬坡类的熵值较小，即误差的概率密度分布较为紧密且集中，也符合上述基于爬坡分类云模型的参数规律。

根据图2、附录A 图A4 和图A5 可知，上爬坡类和下爬坡类的超熵比较大，因此，误差云滴分布都比较分散，这是由于爬坡事件发生时风电数据的随机性较大，不确定性较强。而AR 模型误差、MRF 误差的非爬坡类（见图2（c）、图A5（c））超熵较小，云滴分布更为集中。BP 神经网络非爬坡类误差云模型的超熵略大于爬坡类，说明非爬坡类误差的集中分布趋势较弱且波动频繁。这是由于BP 神经网络是一个模式复杂的非线性自适应动态处理系统，存在局部极小化问题，在无先验信息的支持下，BP 神经网络对爬坡事件和非爬坡事件的风电功率学习能力不足，造成误差数值虽整体差距不大但波动频繁，甚至出现非爬坡类的超熵略大于爬坡类的情况。

3.2 爬坡段预测误差区间评估结果分析

基于3.1 节，将经过爬坡识别分类后的误差类别数据按原有的时间序列顺序与风电功率和爬坡特征数据组合形成3 个新的数据集，分别代入BP、Elman、LSTM、门控循环单元（GRU）以及宽度学习系统（broad learning system，BLS）这5 种神经网络的评估模型中训练。基于Elia 网站数据，从模型输入中关于爬坡特征的分析和与不同误差分布模型的对比两方面说明本文所提模型在爬坡段进行预测误差区间评估的优势。以LSTM 网络模型进行区间评估为例，得到的预测误差爬坡类型预测结果如附录A 图A6 所示，其中爬坡分类分为3 类，每一类的曲线分别对应于相应颜色的区域里。以冬季的Acc结果为例，见附录A 表A3，以说明评估方法判断误差类型的准确性。

3.2.1 爬坡段关于爬坡特征的分析

本节研究对比了未考虑爬坡特征而仅将风电功率作为评估模型输入的方法和本文方法的区间评估效果，以分析模型在建立爬坡特征、风电功率与误差类型的映射关系后对区间评估结果所带来的影响。由于本文基于爬坡事件特征区间评估，为了更好地评价模型性能，仅计算爬坡段评估区间覆盖率IRPICP和爬坡段区间平均带宽IRPINAW。4 个季节的评估结果依次见附录A 图A7 至图A10、表1。在同样季节、数据来源、评估模型的情况下，在模型输入数据中考虑爬坡特征更有利于模型学习爬坡特征、风电功率与误差类型的映射关系，并可根据不同类型的爬坡评估误差区间范围得到更加可靠的评估结果。

表1 冬季不同输入下爬坡段的IRPICP和IRPINAW (a=1)Table 1 IRPICP and IRPINAW of down-ramp section with different inputs in winter (a=1)

以表1 数据为例，本文方法考虑了爬坡特征，其中AR 模型和BP 模型误差的IRPICP均高于0.85。针对爬坡段的区间评估，对于3 种评估模型而言，LSTM 网络评估模型具有更好的评估性能，其中AR 模型和BP 模型误差的IRPICP均达到了0.91 以上，对具有更强波动性、更难以预测的MRF 误差的IRPICP也达到了0.82。而且LSTM 网络评估模型在保证了IRPICP较高的情况下，其IRPINAW在3 种模型中也属于较小的，满足2.3 节所述2 个评价指标的特点。LTSM 网络评估模型之所以能在爬坡段具有更好的评估效果，正是因为模型输入中不仅仅只有风电功率数据，采用按原始时间序列顺序组合的功率和爬坡特征作为LSTM 网络评估模型的输入可以使其充分发挥挖掘数据时序性规律的优势。GRU 评估模型与LSTM 网络评估模型同属于循环神经网络的改进模型，能学习风电数据中的时间关系，其IRPICP达到0.9。BLS 评估模型的网络结构能随着学习不断改变，也具有较好的评估效果，其IRPINAW较小。

以冬季的数据为例，得到不同误差数据来源不同爬坡类别下的IPICP如附录A 表A4 所示。根据表A4 并结合表A2，可以得出不确定性强、超熵较大的爬坡类IPICP略低于非爬坡类IPICP，其中下爬坡类的超熵又小于上爬坡类的超熵，因此其不确定性更弱数据稳定性更高，继而下爬坡类的IPICP略优于上爬坡类的IPICP。

附录A 表A5 至表A8 所示为提前4 h 的区间评估结果。以表A8 中冬季提前4 h 区间评估结果为例，提前4 h 的区间覆盖率略低于单步预测，在本文方法使用LSTM 网络和GRU 评估模型时，区间覆盖率能达到0.85，具有较好的预测效果。且本文方法的区间覆盖率要高于未考虑爬坡特征的方法，本文方法的精度基本高于0.8，具有良好的预测效果，但区间平均带宽也略大于未考虑爬坡特征的方法。由于MRF 波动性更强，为保证其预测精度，所以区间覆盖率也较大。

3.2.2 不同误差分布模型的对比

本节通过与传统的基于概率分布模型的误差区间评估方法对比，分析本文所提方法的性能。正态分布、t分布和传统云模型通过拟合预测误差得到置信水平为90%区间评估结果，本文所提方法中以LSTM 网络评估模型为例，基于此所得的4 个季节、3 种误差来源的爬坡段评估区间覆盖率IRPICP和爬坡段区间平均带宽IRPINAW和4 个季节的评估结果依次如附录A 表A9 至表A11、表2 所示。

表2 冬季不同模型下爬坡段的IRPICP和IRPINAW (a=1)Table 2 IRPICP and IRPINAW of down-ramp section with different models in winter (a=1)

根据正态分布、t分布和传统云模型所得的评价指标结果可知，3 种方法的IRPICP数值较高是建立在IRPINAW值较大的基础上。例如表2 中冬季AR 模型误差基于正态分布的IRPICP数值略高于本文方法（0.68%），但IRPINAW值却增高了27.98%；而基于传统云模型的爬坡段评估区间覆盖率虽然低于本文方法，但其爬坡段区间平均带宽更宽。这是因为传统云模型对整个预测误差序列进行拟合，而爬坡事件中容易存在较大误差，造成较宽的爬坡段区间平均带宽。爬坡段区间平均带宽越宽，在实际运用中电网需要留有的裕量就越大。但由于爬坡事件在风电序列中属于小概率事件，在保证了良好的区间覆盖率的基础上，不需要为小概率事件留有过多裕量，所以本文方法更符合电网的经济运行，即在评估过程中将误差分类云模型与神经网络模型相结合的本文方法，有益于获得爬坡段评估区间覆盖率高且爬坡段区间平均带宽小的评估结果。

3.3 预测误差区间评估结果分析

本节基于3.2 节的数据源，对整个风电功率序列数据的预测误差区间评估结果进行分析，求得置信水平为90%的评估区间覆盖率IPICP和区间平均带宽IPINAW可以比较不同季节、不同误差数据来源下3 种区间评估方法的性能，见附录A 图A11。根据图A11 中的数据可以看出，误差来源、季节、评估模型的不同均会使得评估指标结果不同，且相同情况下IPINAW越大，IPICP也就越高。但就整体结果而言，3 个网络评估模型的评估性能相近，即不同的评估模型给误差区间评估带来的影响不大。

如图3 和附录A 图A12 所示，以LSTM 网络评估模型得到的区间评估结果为例。图3（a）至（c）的区间评估结果的误差来源依次为AR 预测误差、BP预测误差和MRF 误差。

图3（c）中MRF 误差波动性更大，数据的规律性更难以被挖掘，其数据之间的非线性关系更难以被评估模型学习到，所以在预测误差突增或骤减时存在少量超限的情况，即误差的分布特性与原始点预测方法也息息相关，点预测方法得到的误差变化趋势越复杂就越难以预测。由图3 可以看出，发生风电爬坡事件且波动较频繁时，如样本点400 至样本点450 区域内，评估模型得到的误差区间的上限和下限也能反映出相应的数据波动并包络实际输出。总体而言，本文所提方法能够有效提高出现风电爬坡事件、波动频繁时的预测可靠性。

图3 LSTM 网络模型的预测误差区间评估结果(a=1)Fig.3 Interval estimation result of forecasting error based on LSTM network model (a=1)

4 结语

传统的区间评估方法难以在发生风电爬坡事件时有良好的评估效果，本文结合风电预测误差数据的分布特性，提出一种基于爬坡分类误差云模型的区间评估方法。首先，基于爬坡特征对风电功率预测误差数据进行分类；然后，将风电功率和爬坡特征作为输入数据，误差类别作为输出数据，按照原时间序列顺序组成数据集，建立评估模型得到评估区间。

本文利用云模型能有效挖掘不同爬坡类型的风电功率预测误差特点，使得采用神经网络建立的评估模型能够更有效地学习到风电功率、爬坡特征与预测误差之间关系，以得到更为准确的误差区间评估结果。基于模型评价指标，对Elia 网站风电样本进行实例分析，得到本文方法能同时保证较高评估区间覆盖率和较小区间平均带宽，其中LSTM 网络模型具有更好的评估性能，评估区间覆盖率能够达到0.91 以上。通过与不同输入数据、不同评估模型的对比，验证了本文所提基于爬坡特征的误差区间评估方法的可行性。而如今面临日益增长的风电装机容量，对单个风电场进行误差区间评估越来越难以满足电网调度的需求。因此，仍需进一步探索风电场集群功率的爬坡特征以及预测误差分布特性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。