进气压力及流量对自调型J-T制冷器性能的影响

2022-06-09苏鹏翼赵利明徐长彬

激光与红外 2022年5期

苏鹏翼,赵利明,徐长彬

(华北光电技术研究所,北京 100015)

1 引言

自调机构是自调型J-T制冷器控制节流流量的关键结构之一。近年来国内外学者对影响自调机构性能的结构参数[1-2]、运行参数[3]等进行了大量研究工作。但现有研究结果仍未有效解决因自调机构设计不合理造成制冷器间歇性喷液等稳定性较差的问题[4],尤其当气瓶为气源时,随着瓶内压力逐渐降低,自调结构的阀针不断运动,导致制冷器流量变化范围更大,稳定性变差。针对该问题,本文建立理论模型,研究了不同高压流体进气压力、流量对制冷器不同区域流体的压力场、温度场及阀针插入深度的影响规律。

自调型J-T制冷器系统主要由换热器及自调机构两部分组成,系统如图1所示[5]。换热器包括翅片管、芯管及外部壳体等结构,自调机构主要由阀针、阀体、传动机构及芯管内的自调元件构成,其中自调元件可采用波纹管或记忆合金弹簧等可变形元件。

节流前的高压流体压力是分析自调机构力学分析的重要参数之一[6],但是该压力值不易测量,且受高压流体进气压力、流量及热交换器结构等因素的共同影响。为更准确地分析制冷器流体对自调机构的影响,本文对换热器热交换过程及自调机构节流过程分别建模,耦合分析流体对自调机构的影响规律。

2 理论模型

2.1 换热器理论模型

热平衡方程法是计算换热器温度及压力分布常用方法之一。Gupta等人[7]利用热平衡方程法分析了翅片管高度、内径、制冷器与外壳间隙等结构参数对换热性能的影响规律。Zhou等[8]基于熵增理论分析了制冷器换热器部分的做功能力损失。Hong等[9]利用热平衡方程法对制冷器理论制冷量、有用功损失等参数进行分析及预测。Tzabar[10]、肖日仕[11]结合模拟与试验,改进热平衡方程法模型,证明了模型对进出口压力及温度模拟结果具有较高的准确性。

Damle与 Atrey[12]、Cao等人[13]研究结果表明:毛细管沿程的J-T效应是不可忽略的,本文将沿程的J-T效应引入到热平衡方程法模型中。同时,现有模型对芯管及其内充气体的温度分布规律的研究较少,该区域可显著影响自调元件的形变过程。此外,现有模型求解时常将需要测量的低压流体入口处压力及温度作为定解条件[10-11],不利于自调型制冷器的设计计算。本文将在前人模型的基础上,采用考虑了沿程J-T效应的热平衡方程法,以易测量的低压流体出口压力作为定解条件,求解制冷器高低压流体、芯管内部各区域的压力、温度等参数。

在高压与低压流体模拟计算过程中,考虑了节流效应的气体焓值采用公式(1)计算[12],假设低压气体入口处状态为饱和蒸汽。

Δh=cpΔT-μJTcpΔp

(1)

式中,Δh为单元内流体焓变;μJT为节流系数;cp为比热;Δp为压降。

在芯管及内充气体模拟计算过程中,假设内充气体均为气态氮气,稳定工况下内充氮气与芯管间为导热过程,芯管与低压流体间为对流换热。芯管及内充气体两个区域的传热方程可统一为式(2)；利用公式(3)将芯管、内充气体换热与高压低压流体换热耦合。芯管及内部气体两端为绝热边界条件[13]。

hlAt(Tl-T)=0

(2)

Ql=Qh+hlAt(T-Tl)

(3)

式中,T为单元内芯管或内充气体的温度;Tl为对流换热过程中流体温度;Acx与Acr分别为每个单元轴向x与径向r导热过程的换热面积;At为对流换热过程的接触面积。低压流体的吸热量Ql由高压流体的放热量Qh与芯管对流换热量组成。

本文所采用的热平衡方程法的控制方程及参数计算公式汇总至表1。将未考虑与已考虑J-T节流效应的模型分别记作模型1、模型2,将同时考虑J-T节流效应及芯管内部换热的模型记作模型3。

表1 热平衡方程法的参数公式及控制方程汇总表[11-12,15]Tab.1 Summary of governing equations of heat balance equation method

2.2 自调机构理论模型

对于波纹管、记忆合金弹簧两种自调机构,阀针的插入深度xL是影响流量的关键因素之一。阀针与阀体的结构示意图如图2所示。

图2 自调结构阀针阀体结构示意图Fig.2 Structure diagram of self-adjusting valve needle and valve body

改变阀针的插入深度,调节制冷器的流量。通过节流孔流量m的经验公式为[14]:

(4)

(5)

(6)

式中,Ao表示阀针与节流孔间的通流截面积;P与ρ分别为节流前的气体压力及密度;Do为节流孔孔径;Dt为阀针插入节流孔内的最大截面直径;θ为阀针的锥角。

基于上述两个结构的模型,对J-T制冷器的性能参数进行分析求解。

3 结果分析

3.1 换热器模型验证

利用肖日仕[11]、Ng等人[16]研究的制冷器结构(分别记作结构1、结构2)及试验数据对上述模型进行验证,换热器的结构参数如表2所示。模拟数据与试验数据对比结果如表3所示。

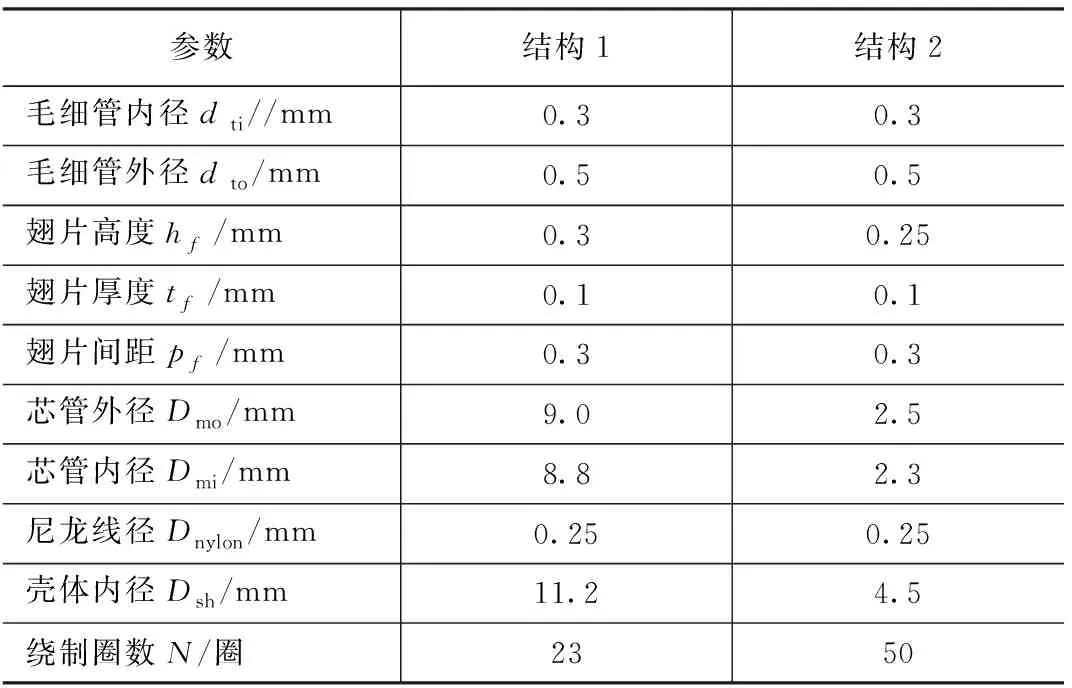
表2 换热器结构参数[11,16]Tab.2 Structural parameters of heat exchanger

对比表3试验数据与模拟结果可知,尽管两种制冷器结构参数、工质及边界条件存在差异,三种模型对低压流体出口温度Tlo的模拟值准确性均比较高,与试验值的最大偏差为2.78 %。与模型1相比,考虑了J-T节流效应的模型2与模型3的低压流体出口温度值Tlo与试验值更接近,最大偏差减小至1.38 %,准确性更高。模型2与模型3的计算结果接近相等。

表3 模拟数据与试验数据对比结果[11,16]Tab.3 Comparison results of simulation and test data

图3示出了制冷器结构1在高压流体进气压力为20.08 MPa时,三种模型模拟的高压与低压流体温度随换热器长度的变化规律。

图3 流体温度随换热器长度的变化规律Fig.3 Variation of fluid temperature with heat exchanger length

由图3及公式(1)可知,由于模型2与模型3考虑了节流效应,该过程节流系数μJT>0,因此模型2与模型3的高压与低压流体温度模拟值较模型1更低。模型3的低压流体的进出口温差模拟值略微高于模型2,其原因为低温端低压流体的部分冷量经芯管及其内部的气体传递到高温段,换热量略微增加,换热器内部温度场更均匀。

换热器不同区域的换热量随其长度的变化规律如图4所示,由图4可知,随着换热器长度增加,高压与低压流体温度差增大,导致换热量迅速增加。但是在芯管及内部气体两端的绝热边界条件下,从芯管及其内部传递的换热量较少,仅占高压与低压流体间总换热量的0.08 %。因此,模型2与模型3的温度场基本一致。

图4 换热量随换热器长度的变化Fig.4 Variation of heat exchange with heat exchanger length

图5与图6分别示出了流体压力及密度随制冷器长度的变化。由图5可知,随着换热器长度增加,高压流体压力显著减小,由20.08 MPa降低至10.68 MPa(模型2)；低压流体入口压力模拟值略高于出口压力约0.56 kPa,因此可忽略低压流体的压降。由图6可知,随温度的降低,高压流体与低压流体的密度显著增加。

图5 流体压力随换热器长度的变化Fig.5 Variation of fluid pressure with length of the heat exchanger

图6 密度随换热器长度的变化Fig.6 Variation of density with length of heat exchanger

对比三种模型可知,考虑节流效应后,高压与低压流体总压降较模型1更小。分析其原因可知,考虑节流后温度模拟值较低,流体密度较高。将动量微分方程变形为式(7),其中,等号右侧第二项为流体可压缩性产生的压降；数据表明,其数值远小于右侧第一项,部分文献已忽略[7]；忽略第二项后的压降dP与密度值ρ呈反比,导致模型1的压降低于模型2与模型3。模型2与模型3的压降及密度无明显差异。

(7)

3.2 换热器性能分析

由前一小节分析可知,考虑节流效应的模型2与模型3模拟值准确性更高。为获得换热器内部各区域更准确的温度场及压力场,本小节利用模型3分析不同进气压力及流量下换热器的性能参数变化规律。

图7示出了不同高压流体出口压力随进气压力、流量的变化规律。由图7可知,随着进气压力增加,高压流体部分的总压降减小；随着流量增加,流体压力损失越大。分析原因认为:随着压力增加,高压流体密度增加导致沿程摩阻减小；由式(7)可知,压降随流量平方的增加而增加。

图7 高压流体出口压力随进气压力、流量的变化规律Fig.7 Effect of flow on outlet pressure of high pressure fluid

不同进气压力及流量下节流后干度变化如图8所示。由图8可知,随着流量增加及压力减小,节流后的干度逐渐增加,表明单位质量流量的工作制冷能力下降。当进气压力16 MPa、流量为0.30 g/s时,干度值为0.915,即节流口工质接近饱和蒸汽。由此推断,若进一步减小进气压力或增加流量,节流后的工质可能由湿蒸汽转变为干饱和蒸汽或过热蒸汽,制冷器节流后温度将大幅度变化,制冷能力不足。

图8 节流后干度随进气压力、流量的变化规律Fig.8 Effect of flow on dryness after throttling

采用公式(8)计算制冷器理想状态的制冷量Qideal[11],制冷量随进气压力、流量的变化规律如图9所示。

Qideal=m(hho-hli)=mhpo(1-x)

(8)

式中,hpo为汽化潜热;x为干度。

由图9可知,当流量相同时,制冷器制冷量随进气压力的增加而增加；当进气压力相同时,制冷器随流量先增加后减小,该现象与Ardhapurkar与Atrey的研究有相似的结论[17]。结合式(8)可知,制冷量与质量流率呈正比,随干度增加而减小,因此制冷量存在最大峰值。

图9 制冷量随进气压力、流量的变化规律Fig.9 Effect of flow on refrigerating capacity

3.3 芯管及其内部气体温度场分析

不同流量及高压气体进气压力下,换热器内部不同区域温度场分布如图10、图11所示,沿径向方向依次表征芯管内氮气、芯管、低压流体及高压流体的温度值。

图10 当Phi=20.08 MPa时不同流量下换热器各区域温度云图Fig.10 Variation of temperature cloud chart with length of heat exchanger when Phi=20.08 MPa

由图10可知,芯管外部的高低压流体间存在较大的温度梯度；芯管及其内部温度沿轴向及径向方向逐渐降低；随着流量减小,制冷器冷段的区域范围逐渐减小。其主要原因为,流量越大,节流后低压流体携带的冷量越高,导致高压流体温度、密度及比热下降越迅速。

分析图11可知,随着压力增加,换热器冷段的区域范围逐渐减小。分析原因认为,随着进气压力增加,高压流体流体密度及比热增大,导致高压流体温度不易下降；低压流体密度及比热较小,其温度易随高压流体不断升高。

图11 温度云图随换热器长度的变化(m=0.3 g/s)Fig.11 Variation of temperature cloud chart with length of heat exchanger when m=0.3 g/s

3.4 自调机构分析

不同高压流体进气压力及流量下,阀针的插入深度变化规律如图12所示。由图12可知,高压流体进气压力越大,不同流量下的阀针插入深度越大。当m≤0.1 g/s时,不同流量对应的插入深度只在268～276 μm之间变化,即当流量越小时,阀针插入深度越接近恒定值,自调机构无需匹配运动。当进气压力越高时,由于流体密度越大,流量随插入深度的变化越剧烈,该现象可能导致制冷器流量不稳定,甚至不易调节,失去自调功能。

图12 高压流体进气压力对插入深度的影响Fig.12 Effect of inlet pressure of high pressure fluid on insertion depth

图13示出了阀针的插入深度对高压流体进气压力及节流孔初始孔径的变化规律。由图13可知,流量越小,阀针插入深度值越大；随着节流孔孔径及高压气体进气压力的增加,不同流量对应的插入深度值逐渐接近,该现象易导致流量随插入深度迅速变化,不易调节；相同流量下,随节流孔初始直径及进气压力增加,阀针插入深度的变化幅度逐渐减小,即自调机构需匹配的运动范围越小。由此可知,节流孔初始孔径具有最优解。

图13 节流孔初始直径对插入深度的影响Fig.13 Effect of initial orifice diameter on insertion depth

进一步分析图13可知,当流量m≤0.1 g/s时,不同进气压力(20～30 MPa)对插入深度变化幅度的影响可以忽略,即流量较小时,压力变化不会显著改变插入深度,制冷器运行更稳定。由此推断,为提高流量的可调节性,在孔径满足最大流量要求的前提下,可选择较小孔径的节流孔。当流量m>0.1 g/s时,可根据插入深度变化幅度选择与之匹配运行的自调元件。

阀针锥角对阀针插入深度的变化规律如图14所示。由图14可知,随着锥角增加,不同进气压力下的插入深度变化范围逐渐减小；但由公式(4)～(6)可知,锥角越大,流量变化越剧烈,不利于流量的稳定。