基于模体的低压配电网负荷波动特性分析

李知艺，马翔宇，2，于 群，辛焕海，鞠 平，3

（1. 浙江大学电气工程学院,浙江省杭州市 310027；2. 浙江大学工程师学院,浙江省杭州市 310015；3. 河海大学能源与电气学院,江苏省南京市 211100）

0 引言

在“双碳”目标驱动下,中国电力系统正朝着以新能源为主体的新型电力系统快速演进。一方面,风电、光伏等新能源发电具有明显的随机性和间歇性,给电力系统电力电量平衡带来严峻挑战,函须充分挖掘海量分散负荷的可调控潜力；另一方面,分布式光伏、储能和电动汽车等新设备在低压配电网中的渗透率不断提升［1-2］,负荷内涵进一步扩充,负荷波动愈加随机,演变态势日趋复杂,函须充分认知负荷特性,为负荷调控奠定决策基础。与此同时,随着物联网设备的广泛部署,用户侧累积了海量的量测数据,为精准刻画与认知负荷特性提供了数据基础支撑。在此背景下,挖掘用户侧量测数据的隐藏价值,拓展负荷特性分析维度,解析负荷波动规律,具有重要的理论价值与工程应用前景。

目前,数据驱动的负荷波动特性研究大多聚焦于宏观统计特征,尚未充分挖掘不同时空尺度下负荷波动的细节特征及其内涵。例如,文献［3］基于年负荷曲线,计算了负荷平均值、最大值与最小值等指标,并评估了疫情对部分欧洲国家电力系统的影响；文献［4］基于日负荷曲线,对比分析了疫情对英国电力系统的影响,并在此基础上预测了受疫情影响的日负荷值；文献［5］应用机器学习方法,分析了美国得克萨斯州日负荷峰值与影响因素的关联性。然而,仅根据最大值、平均值等统计指标,难以有效区分具体的演变态势。

此外,低压配电网中负荷点多量广,难以直接调控,因此,通常从集群的角度对负荷波动特性进行刻画分析。然而,负荷集群波动特性并非单个负荷波动特性的简单叠加。常见的负荷集群特性研究思路主要有聚合和聚类2 种。具体而言,聚合方法主要关注集群模型的一体化构建及其参数辨识问题［6］,如文献［7-8］基于等效热参数模型对空调负荷聚合功率进行建模,并采用参数辨识的方法聚合空调负荷。聚类方法可以细分为直接法和间接法［9］,其中,直接法的思路是直接对负荷曲线进行聚类,如文献［10-11］分别基于k-means 算法和层次聚类法对历史日负荷曲线进行聚类,以提取集群日负荷特征；间接法则是先提取负荷特征,再根据特征进行聚类分析,如文献［12］首先提取日负荷率、日峰谷差率、日最大利用时间等特征,在此基础上应用熵权法实现日负荷曲线聚类。然而,在不同时空尺度下,负荷集群的波动特性呈现较大差异,仅靠聚合建模或聚类分析难以精细化刻画负荷集群的内部差异特征和整体演变态势。

本文基于模体（motif）理念构建了数据驱动的低压配电网负荷波动特性分析框架,并从个体和集群2 个维度提出了负荷波动模式认知与特征挖掘的新方法。本质上,模体提供了“以小见大”的新分析视角,通过从复杂多样的负荷曲线中提取波动态势的基本组成单元,有助于更全面地解析负荷波动规律与内涵,进而精准辨识负荷态势演变规律。

1 数据驱动的负荷波动特性分析框架

1.1 模体概念及内涵

模体首见于生物学研究,原指高频重复出现、可能具有分子功能的脱氧核糖核酸（deoxyribonucleic acid,DNA）序列［13］。这一概念后续在多个专业领域得到了引申应用,如附录A 图A1 所示。以复杂网络理论研究为例,模体指高频重复出现、非随机的基本网络结构［14］,通常仅由少量节点及其连边所构成。同理,高频重复出现、能够表征基本变化模式的时间序列片段也可被定义为模体；相关模体理念已被成功用于车辆驾驶行为［15］、心律［16］、股票［17］等多种场景下的趋势分析。

随着智能电表等量测设备的普及,用户侧积累了海量、固定时间间隔采集的量测数据（比如有功功率、温度、湿度等）,其本身可以被有序排列为时间序列。通过挖掘相关模体,有助于揭示组成负荷波动模式的基本单元,刻画负荷波动态势演化的内在规律,进而增强对负荷波动特性的认知。图1 以负荷时间序列的波动特性分析为例,揭示了模体的构建原则及其与传统研究视角的区别。图1 中t和i表示不同时刻。主要区别如下:

图1 基于模体的负荷波动特性分析框架Fig.1 Framework of motif-based analysis on load fluctuation characteristics

1）宏观层面主要关注较长时间窗内（连续多个时间点）的负荷波动态势。常见的分析结果为负荷峰谷值、平均值、持续时间等统计指标,多用于刻画整体性、趋势性的负荷变化情况。

2）微观层面主要关注连续2 个时间点的负荷波动情况,其代表了负荷最基本的波动行为（即增长、降低或不变）,但难以捕捉负荷变化的关联性和规律性,分析结果所含信息价值相对较低。

3）模体层面则关注少量（通常3～4 个）连续时间点内负荷波动的统计规律,其相较于宏观层面能表征更丰富的波动细节特征,而相较于微观层面能更全面地刻画负荷连续波动的关联和组合特征。

值得指出,这3 个层面的分析结果并非简单叠加关系。对负荷时间序列而言,挖掘和分析模体,能有效承接和支撑传统方法在宏观和微观层面下的分析结果,并突破传统方法研究范式上的局限性。

1.2 基于模体的分析框架

图1 展示了基于模体的负荷波动特性分析框架,旨在以简单、高效的方式挖掘海量量测数据蕴含的隐藏价值,进而从新的视角剖析负荷波动的本质机理。具体来说,该框架包括如下4 个关键部分:

1）数据预处理:从量测数据中提取研究对象,并针对数据失步、异常等问题进行数据清洗操作。

2）模体定义:根据特定的分析需求,定义单个或多个时间序列的模体构建规则。比如,可以根据波动幅值的相对大小直接定义模体,无须人为设定阈值,从而避免主观因素干扰；也可以通过划定多个阈值并按负荷波动幅值占负荷峰值的百分比定义模体,从而更好地耐受噪声干扰。

3）模体挖掘:根据模体构建规则,以滑动时间窗的方式对单个或多个时间序列逐次分解并提取模体。模体挖掘并不局限于量测数据自身的时间尺度,可根据实际需要挖掘相关模体,进而灵活分析不同时间尺度下的负荷波动情况。比如,以日负荷功率平均值构建时间序列,在此基础上挖掘以日为时间尺度的模体。

4）模体分析:结合挖掘到的模体特征及其统计规律,综合分析单个负荷或负荷集群的波动特性。一方面,可以根据分析结果捕捉和判定不同时空尺度下负荷波动的异常态势；另一方面,通过对比分析不同外界因素作用下的模体挖掘结果,有助于解析负荷波动特性的关联影响因素。

2 单个负荷的波动特性分析

本章针对单个负荷的波动模式构建模体,进而深入挖掘负荷量测数据的隐含波动规律,提升波动特性分析的精细度。

2.1 模体定义与挖掘

采用滑动时间窗,对长度为n的单个负荷时间序列YI=[yI,1,yI,2,…,yI,n]T进行分割:

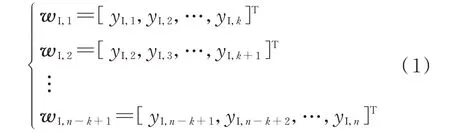
式中:yI,i(i=1,2,…,n)为时刻i的负荷功率量测数据；k为滑动时间窗的长度,通常取3 或4；wI,i=[yI,i,yI,i+1,…,yI,i+k-1]T(i=1,2,…,n-k+1) 为时刻i的一个序列片段。

理论上,滑动时间窗覆盖的每一个序列片段都可形成一个模体,其最多可能有k（k-1）种类型。为方便阐述,将这一类反映单个时间序列波动特征的模体简称为IM（individual motif）。

当k=3 时,可形成最多6 类最基本的模体。典型构建方式如附录A 图A2 所示,分类结果及特征如附录A 表A1 所示。这些模体的具体含义解释如下:

IM-1 主要刻画负荷在某一时间段（连续3 个时间点,下同）呈现单调不增的态势,其数学表达式为yI,i≥yI,i+1≥yI,i+2。

IM-2、IM-5 均能反映负荷在某一时间段先减小后增大的波动情况,其中,IM-2 主要刻画首端时刻负荷值不低于尾端时刻的波动态势,其数学表达式为yI,i≥yI,i+2＞yI,i+1；IM-5 则 与 之 相 反,其 数 学 表达式为yI,i+2＞yI,i≥yI,i+1。

IM-3、IM-4 均能反映负荷在某一时间段先增大后减小的波动情况,其中,IM-3 主要刻画首端时刻负荷值不低于尾端时刻的波动态势,其数学表达式为yI,i+1＞yI,i≥yI,i+2；IM-4 则 与 之 相 反,其 数 学 表达式为yI,i+1≥yI,i+2＞yI,i。

IM-6 主要刻画负荷在某一时间段呈现单调递增的态势,其数学表达式为yI,i+2＞yI,i+1＞yI,i。

2.2 模体分析

根据定义,模体可以表征负荷在某一时间段的基本波动模式。因此,通过统计分析不同模体出现的次数及其分布情况,可以有效关联负荷宏观特性与波动细节特征。进一步地,可构建模体转移网络,刻画分析连续时间段内波动模式的转移关系,进而更充分地挖掘负荷波动态势演变的内在规律。理论上,给定wI,i=[yI,i,yI,i+1,…,yI,i+k-1]T和wI,i+k=[yI,i+k,yI,i+k+1,…,yI,i+2k-1]T2 个时间段所对应的模体,最多可能有k2（k-1）2种转移模式。在此基础上,通过统计分析模体转移模式的概率分布情况,可以更深入地挖掘负荷波动的连续变化信息,从而更全面地刻画负荷波动特性。

2.3 算例验证

选用2020 年8 月中国浙江某地区的真实用电数据集进行数值实验,该数据集囊括了住宿和餐饮业、公共服务及管理组织、工业、建筑业等多个行业的负荷数据,其量测时间间隔为15 min。

取时间窗长度k=3,图2 展示了4 类典型负荷的日负荷曲线及其模体转移图谱。其中,模体转移图谱的纵轴代表前一时段（如yI,i、yI,i+1、yI,i+2）可能对应的6 类模体,横轴表示后一时间段（如yI,i+3、yI,i+4、yI,i+5）可能对应的6 类模体；方块颜色越深,表示该模体转移模式出现的概率越大。

如图2（a）至图2（d）所示,从日负荷曲线而言,商场负荷与医院负荷的宏观统计特征较为相似,但其模体转移图谱存在显著差异:商场负荷的模体转移图谱中,IM-1→IM-1 的颜色较深,表明商场负荷处于连续降低状态的频次较高；而医院负荷的模体转移图谱中,IM-1、IM-6 对应的行、列颜色较浅,表明医院负荷鲜少出现连续增长或降低状态。因此,虽然2 类负荷在宏观层面演变趋势相近,但模体转移图谱提供了全新的视角来清晰反映其内在差异。

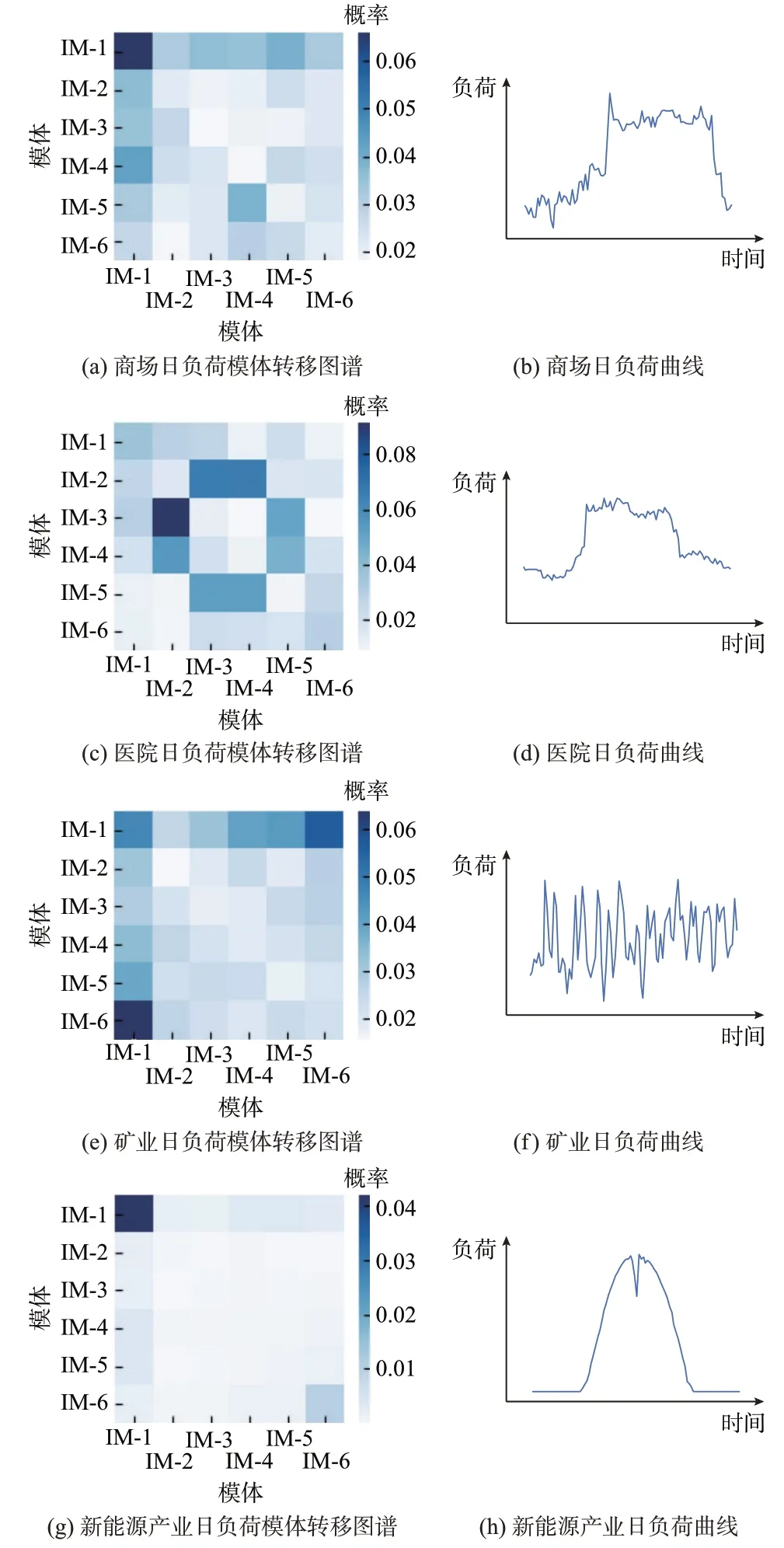
图2 典型模体转移图谱与日负荷曲线对照Fig.2 Comparison between typical motif transfer graph and daily load curve

如图2（e）和图2（f）所示,矿业负荷为冲击负荷,在较短周期内有规律地频繁增加、减小；相应的模体转移图谱左下角IM-6→IM-1 和右上角IM-1→IM-6 对应的色块颜色最深,有效表征了其交替频繁变化的性质。如图2（g）和图2（h）所示,新能源产业负荷为规则的单峰负荷,负荷长时间内单调增加、减少或不变；在模体转移图谱中,只有左上角IM-1→IM-1 和右下角IM-6→IM-6 的色块颜色较深,有效表征了其单调变化的性质。因此,模体转移图谱可以真实还原日负荷曲线展示的宏观变化规律。

3 负荷集群的波动特性分析

本章针对多个负荷的联合波动模式构建模体,进而揭示复杂波动态势的构成规律,增强对分散负荷集群波动特性的辨识能力。

3.1 波动状态表征

针对m个负荷组成的负荷集群,选定长度均为n的同步时间序列Y1=[y1,1,y2,1,…,yn,1]T,Y2=[y1,2,y2,2,…,yn,2]T,…,Ym=[y1,m,y2,m,…,yn,m]T。其中,y1,1为负荷1 在时刻1 的功率量测数据,其余以此类推。进一步可将其表示为如下n×m矩阵:

设定一个长度为2 的滑动时间窗,提取集群内所有负荷在连续2 个时间点的功率量测数据:

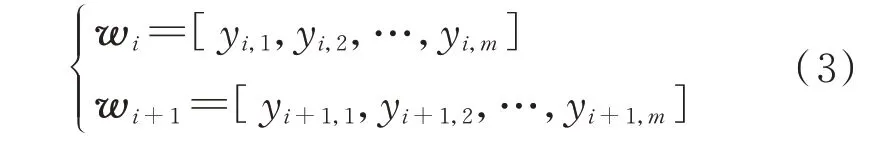
式中:wi和wi+1分别为时刻i和i+1 的集群负荷功率量测数据向量。

在此基础上,定义时段i负荷集群波动状态向量Δ(i):

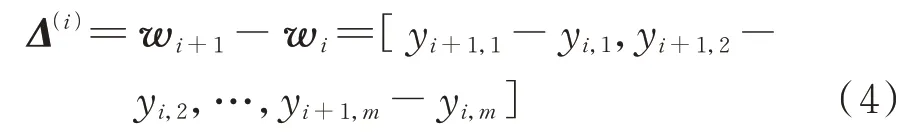
Δ(i)为一个m维向量,聚合表征了集群内所有负荷在该时间段的波动状态,包括波动方向（数值正负）及幅值信息（数值大小）。

3.2 模体定义、挖掘与分析

为进一步刻画负荷集群波动状态的跳变特性,选取合适的评估函数计算连续3 个时间段内波动状态之间的距离关系:

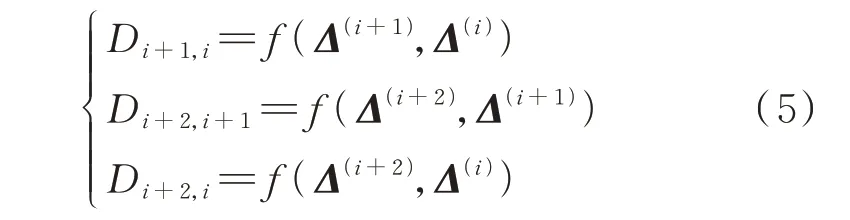
式中:Δ(i)、Δ(i+1)和Δ(i+2)分别为负荷集群在首端、中间、尾端时段内的波动状态向量；Di+1,i、Di+2,i+1、Di+2,i分别为首端到中间、中间到尾端、首端到尾端时段的相对波动距离；f(·)为距离函数,可采用欧氏距离、汉明距离等多种形式。

欧氏距离可以衡量负荷集群波动状态向量在高维空间中的相对距离,聚合表征整体波动方向和幅值信息；汉明距离可以衡量序列间的符号差异性［18］,进而刻画集群内部负荷波动方向的变化比例；不失一般性,下文均采用欧氏距离来刻画波动状态的变化量。值得指出的是,正如三角形的稳定性,通过刻画连续3 个时段的相对波动距离,可以锁定负荷集群的局部波动态势。

图3 举例说明了单个负荷波动与负荷集群波动的对应关系。通过刻画和区分波动状态间的距离,可以将模体的应用从单个负荷推广至负荷集群的波动特性分析。具体来说,可根据连续3 个时段内波动状态跳变距离的相对大小关系,定义和挖掘集群波动模体,进而刻画负荷波动的集群变化特征。

图3 单个负荷波动与负荷集群波动的对应关系Fig.3 Corresponding relation between individual and cluster load fluctuations

为方便阐述,集群波动模体简称为CM（cluster motif）,其 最 多 可 划 分 为6 类。附 录A 表A2 以 二 维平面距离为例,列举了每类模体的构建方式。这些模体的具体含义解释如下:

CM-1 主要刻画连续3 个时段内逐渐远离初始波动状态的趋势,且该趋势逐步加强,波动状态的可预测性低（尤其难以根据首端时段波动状态准确预测尾端时段的波动状态）,其数学表达式为Di+1,i＜Di+2,i+1＜Di+2,i。

CM-2 主要刻画连续3 个时段内波动状态出现转折式变化的趋势,前2 个时段的波动状态较为相似,但最后时段出现突变（尾端时段状态与中间时段状态差别最大,首端时段状态与中间时段状态差别最小）,其数学表达式为Di+1,i＜Di+2,i≤Di+2,i+1。

CM-3 主要刻画连续3 个时段内逐渐远离初始波动状态的趋势,但该趋势逐步减弱,波动状态的可预测性低（甚至难以根据首端时段波动状态准确预测中间时段的波动状态）,其数学表达式为Di+2,i+1≤Di+1,i＜Di+2,i。

CM-4 主要刻画连续3 个时段内波动状态呈现转折式变化的趋势,后2 个时段状态较为相似,但中间时段出现突变（首端时段状态与中间时段差别最大,尾端时段状态与中间时段状态差别最小）,其数学表达式为Di+2,i+1＜Di+2,i≤Di+1,i。

CM-5 主要刻画中间时段的波动状态出现偏离,首、尾两端时段的波动状态更为相似的趋势（尾端时段状态与中间时段状态差别最大,首端时段状态与尾端时段状态差别最小）,其数学表达式为Di+2,i＜Di+1,i≤Di+2,i+1或Di+2,i≤Di+1,i＜Di+2,i+1。

CM-6 主要刻画中间时段的波动状态出现偏离,首、尾两端时段的波动状态更为相似的趋势（首端时段状态与中间时段状态差别最大,首端时段状态与尾端时段状态差别最小）,其数学表达式为Di+2,i≤Di+2,i+1＜Di+1,i。为确保模体定义的完备性,此类模体还包括连续时段内波动差异等距的情况,其数学表达式为Di+2,i=Di+2,i+1=Di+1,i。

通过统计分析6 类CM 模体的出现次数百分比,可以有效辨识负荷集群波动的主导模式及其关联因素。在此基础上,同样可以挖掘模体转移模式,进一步解析负荷集群波动的连续变化特征,进而更精准地推断外界因素影响下的集群波动规律。

3.3 算例验证

选用可持续发展智能数据集［19］进行算例验证。该数据集包括了2016 年114 个单户公寓的电力负荷数据,量测时间分辨率为1 min,共330 d,数据总量约为5 417.28 万条。基于清洗后的数据集,按30 d 为间隔将330 d 划分为11 个月。此外,根据数据集中的温度信息,计算每月平均温度。

图4 展示了6 类CM 模体的出现次数百分比以及平均温度在不同月份的波动情况,可以发现模体出现次数百分比明显受温度影响。如图4 所示,CM-2、CM-4、CM-5、CM-6 这4 类模体的出现次数百分比变化与温度变化呈现正相关性,而CM-1、CM-3 这2 类模体的出现次数百分比变化与温度变化呈现负相关性（即夏季温度上升后,CM-1 和CM-3 出现次数显著减少）。这表明,负荷集群波动特性存在季节性差异,且夏季的负荷波动相较于冬季更为规律（即夏季鲜少出现可预测性较低的负荷波动模式）,可能与用户侧温度敏感型负荷（如频繁启停的电加热设备）占比大有关。附录A 图A3 随机选取了4 个单户公寓在1 月和7 月的负荷功率采样数据进行对比,对上述结论进行了验证。

图4 集群波动模体出现次数百分比与温度相关性Fig.4 Correlation of motif occurrence percentage and temperature

此外,为详细分析负荷集群波动特性在夏季和冬季的差别,分别提取1 月和7 月的所有可能转移模式,并统计其出现频次进行对比分析。如附录A图A4 所示,不同色条颜色及方向代表了不同种类的模体转移模式,色条宽度代表了所对应模体转移模式的出现频次。结果表明,1 月和7 月部分模体的转移模式存在显著差异。具体而言,CM-3→CM-3的转移频次在1 月明显高于7 月,且该月模体转移以CM-3 为主导；1 月的模体转移模式相对清晰,存在主导转移模式,而7 月的模体转移特征更加复杂,但缺乏主导转移模式。以上结果表明,负荷集群的波动态势并非完全随机,而呈现受温度影响的季节性变化特征,能为进一步辨识负荷中的温度敏感部分提供理论指导。

4 结语

本文提出了一种适用于分析低压配电网负荷波动特性的数据分析新思路,分别从个体和集群2 个维度挖掘用户侧量测数据的隐藏价值,旨在进一步拓展负荷特性研究的内涵和方法维度。算例结果表明,本文所提方法能有效挖掘不同类型负荷波动的差异化细节特征,以及温度变化影响下负荷集群波动的差异化聚合特征。因此,通过采用模体刻画和辨识负荷波动特性,可以精细化表征和分析负荷波动的基本模式及其相关影响因素,进而为快速、精准辨识负荷演变态势奠定理论基础。

后续研究将进一步探索负荷模体在异常态势辨识、需求侧响应机制设计等方面的应用。另外,虽然数据分析和利用的效能不断提升,但用户隐私保护的意愿也日益强烈。因此,在后续研究中,将进一步明确模体挖掘与分析的可用数据范畴,增加隐私保护机制,以保障用户敏感信息不被泄露,同时,将进一步探析数据安全对负荷特性研究的影响,研判网络攻击风险对模体挖掘和分析过程的影响机理,进而针对性地设计免疫机制。