单自由度车辆悬挂系统非线性振动特性研究
2022-06-09杨明明
□ 杨明明
武汉铁路职业技术学院 铁道机车车辆学院 武汉 430205
1 研究背景
随着铁路运输的飞速发展和人民生活水平的不断提高,人们对列车的运行速度与舒适性提出了更高的要求,车辆运行速度不断提高所引起的振动问题同样日益突出。车辆悬挂系统的性能直接影响车辆行驶的安全性与平稳性,因此研究悬挂系统对车辆振动特性的影响显得尤为重要。笔者以简化的1/4车辆系统模型为研究对象,对单自由度车辆悬挂系统非线性振动特性进行研究。
2 单自由度车辆系统建模
以1/4车体为研究对象,建立单自由度车辆力学模型,如图1所示。图1中,m1为车体质量,Fs为弹簧恢复力,Fd为垂向减振器阻尼力,z1为车体位移,x0为轨道不平顺度激励。
在这一系统中,悬挂的空气弹簧与液压阻尼器均为非线性,这一结论通过对空气弹簧和液压阻尼器的测试数据拟合得到。
弹簧恢复力Fs为:
(1)
Δx1=z1-x0
(2)
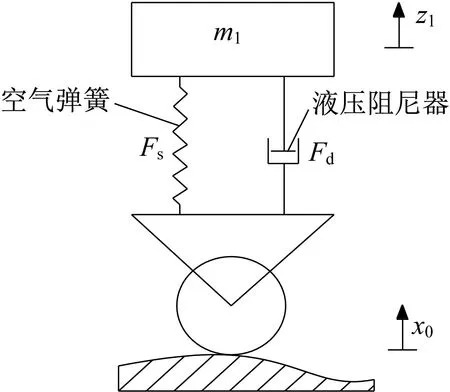
▲图1 单身由度车辆力学模型
式中:k1、k2为弹簧刚度。
垂向减振器阻尼力Fd为:
(3)
(4)
式中:c1、c2为减振器阻尼系数。
3 Melnikov方法分析
系统参数中,m1为42.8 t,k1为1 300 kN/m,k2为5.25×106kN/m,c1为8.5(kN·s)/m,c2为-65.5(kN·s)/m,可以得到发生混沌的U形曲线,如图2所示。

▲图2 U形曲线
斯梅尔马蹄对应一个非常容易把握的混沌不变集,若一个二维离散动力系统具有不会发生混沌的轨道不平度幅值阈值,则此系统会产生斯梅尔马蹄现象。所谓Melnikov方法,即是寻找不会发生混沌的轨道不平度幅值阈值的方法。这一方法是一种对动力学系统进行解析分析的较为成熟的方法。
U形曲线之上表示混沌区域,在此区域内的参数可能会使系统发生斯梅尔马蹄混沌不变集意义下的混沌。U形曲线之下表示非混沌区域,在此区域内的参数不会使系统发生斯梅尔马蹄混沌不变集意义下的混沌。系统发生斯梅尔马蹄混沌不变集意义下的混沌时,轨道不平度幅值的阈值为0.002 45 m。所以在设计悬挂系统时,应尽量选择合适的参数,使轨道不平度幅值的阈值尽可能大,这样车辆在运行过程中才不会发生混沌,从而保证乘客的乘坐安全性和舒适性。
系统发生混沌的轨道不平度幅值阈值受阻尼平方项影响较小,这是因为在一次近似求解过程中,其积分项为0。
当k2与c1变化时,U形曲线的变化分别如图3、图4所示。由图3、图4可知,当轨道不平度幅值的阈值为定值时,发生混沌的角速度有一个范围,并且随着轨道不平度幅值阈值的增大而增大。
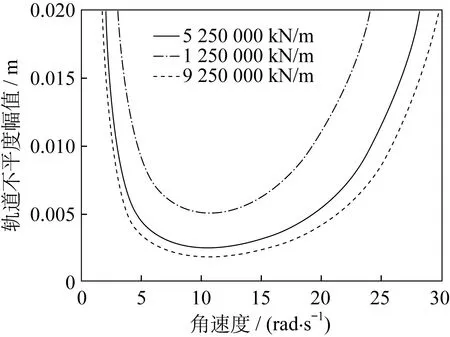
▲图3 k2变化时U形曲线
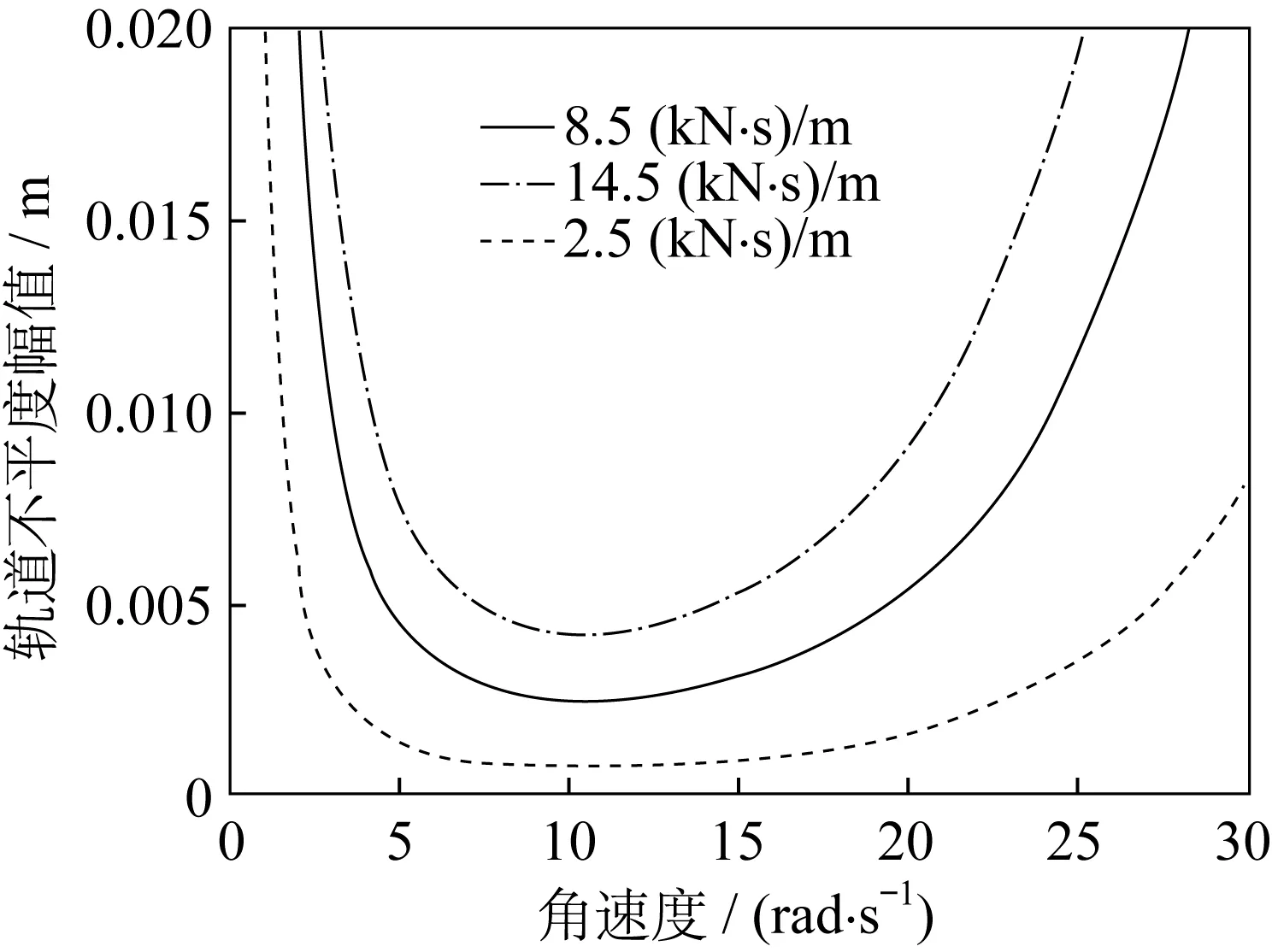
▲图4 c1变化时U形曲线
在一定范围内,当k2增大时,系统发生混沌的区域变大,这说明系统发生混沌的可能性增大。在一定范围内,当c1增大时,系统发生混沌的区域会变小,这说明系统发生混沌的可能性减小。
4 仿真分析
当角速度为10 rad/s时,系统发生混沌时的轨道不平度幅值阈值必须大于0.002 45 m,为了验证这一结论的准确性,进行仿真。
当轨道不平度幅值的阈值为0.002 m时,车体振动相图如图5所示。由图5可以看到,相图为一个稳定的极限环,Poincare映射为一点,可以判定系统此时做周期运动。
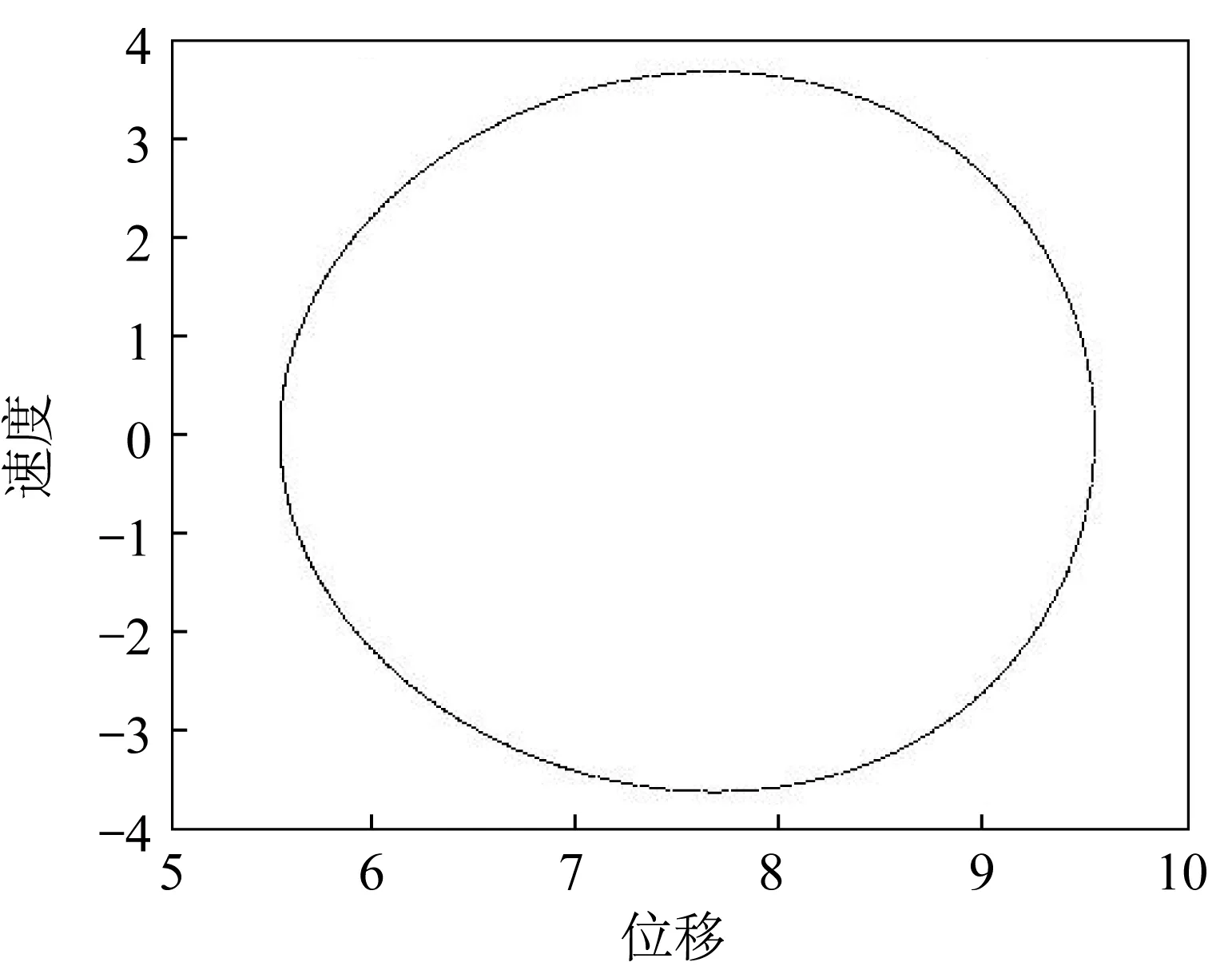
▲图5 轨道不平度幅值阈值为0.002 m时车体振动相图
当轨道不平度幅值的阈值大于0.002 45 m时,系统通过倍周期分岔的形式通向混沌。当轨道不平度幅值的阈值为0.145 m时,系统做单周期运动,如图6所示。当轨道不平度幅值的阈值为0.165 m时,系统做两周期运动,如图7所示。当轨道不平度幅值的阈值为0.171 m时,系统做四周期运动,如图8所示。当轨道不平度幅值的阈值为0.178 m时,系统发生混沌,如图9所示。
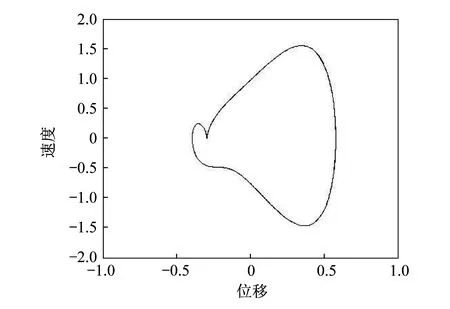
▲图6 轨道不平度幅值阈值为0.145 m时车体振动相图
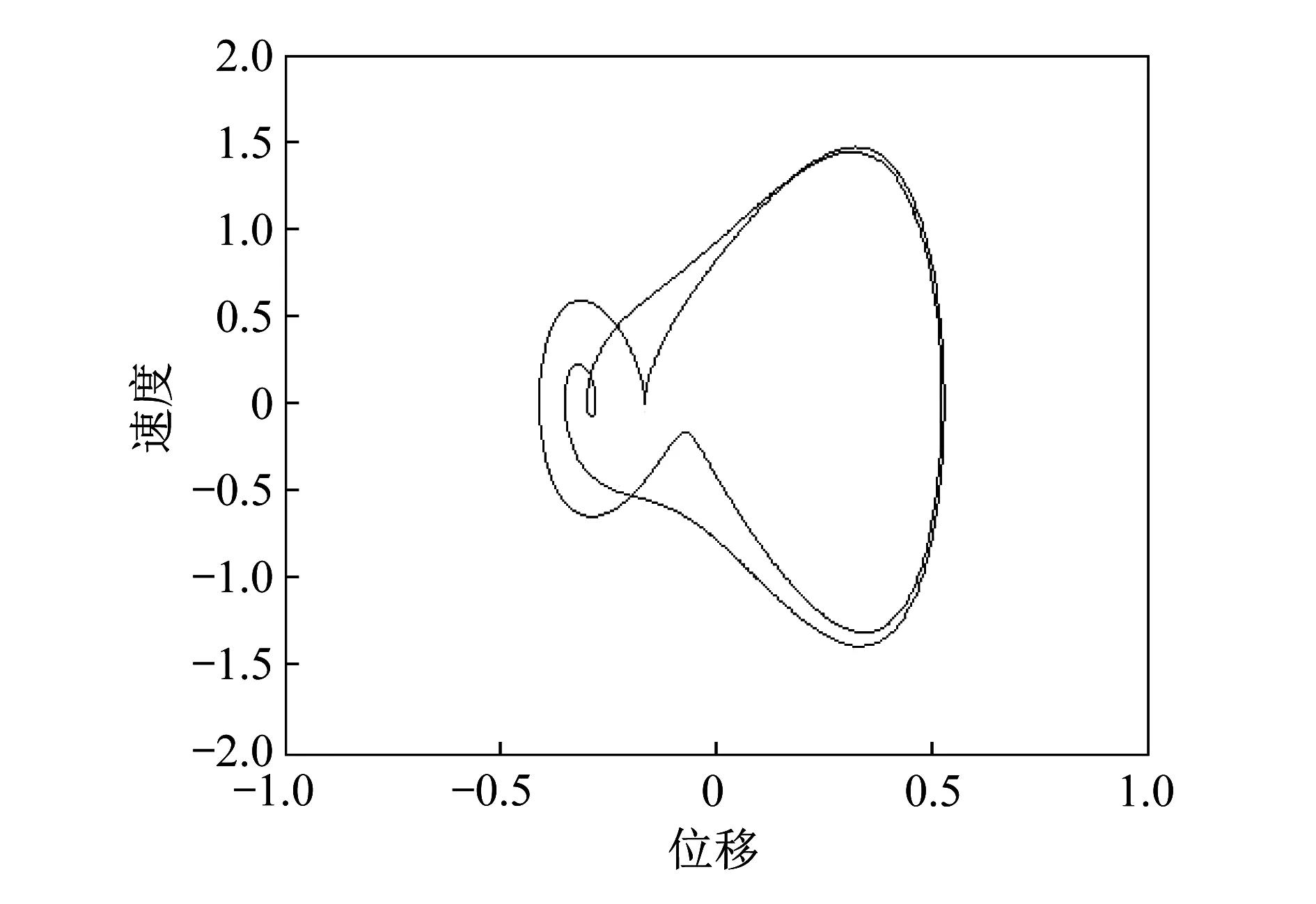
▲图7 轨道不平度幅值阈值为0.165 m时车体振动相图
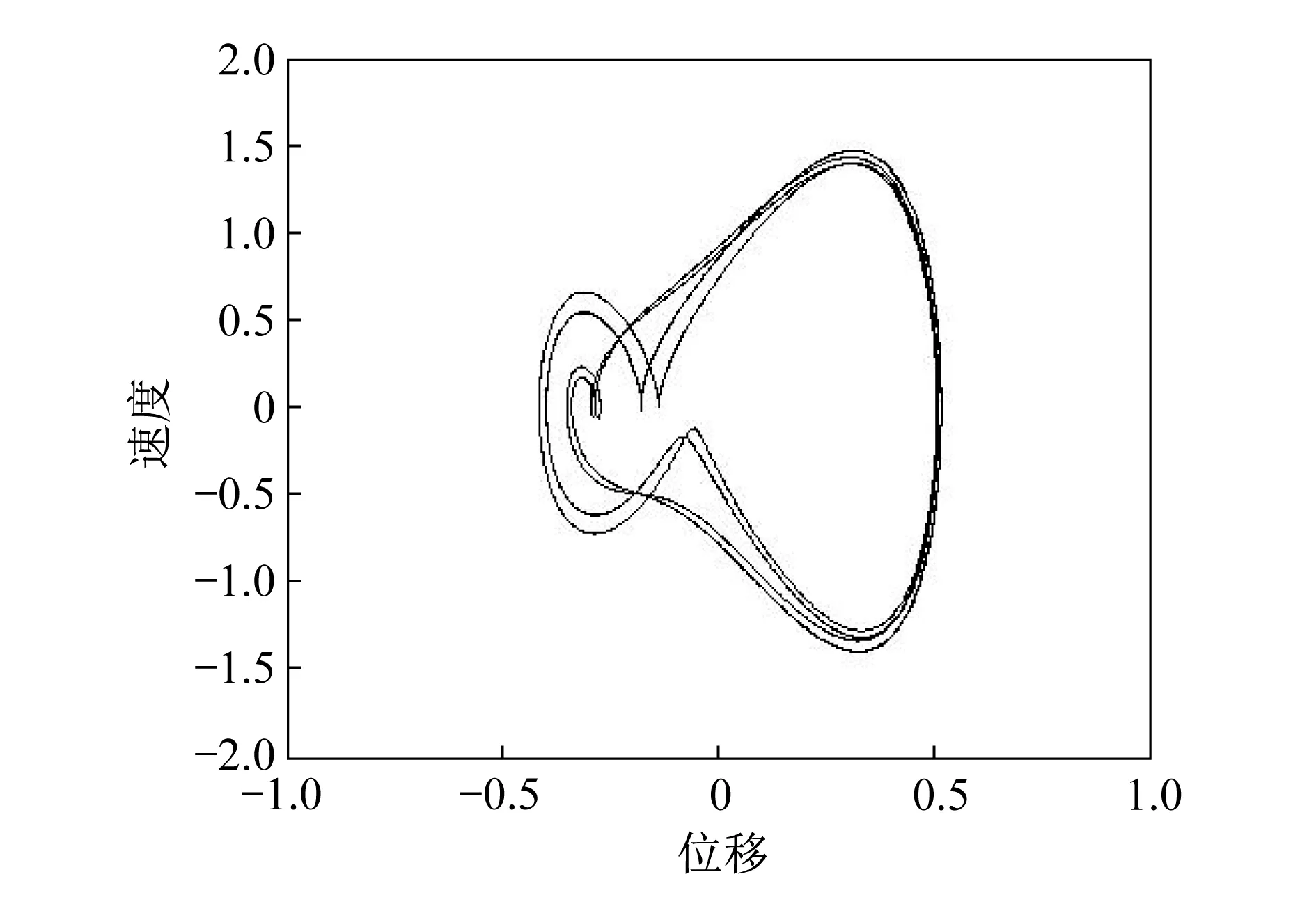
▲图8 轨道不平度幅值阈值为0.171 m时车体振动相图
5 误差原因
由仿真结果得到,系统直到轨道不平度幅值阈值为0.178 m时才发生混沌,与Melnikov方法得到的阈值大于0.002 45 m相比,相差过大,产生了误差。
产生误差的原因主要是,Melnikov方法求出的轨道不平度幅值阈值是发生混沌必要条件,而不是充分条件。系统要发生混沌,必须要满足轨道不平度幅值阈值大于0.002 45 m,但是阈值大于0.002 45 m时,并不一定会发生混沌。
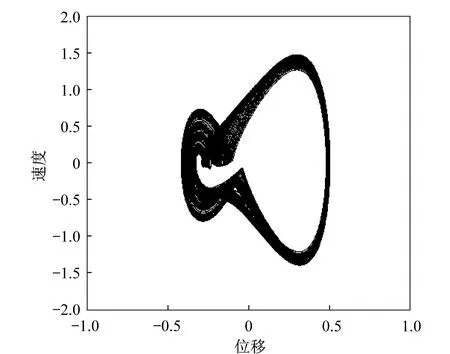
▲图9 轨道不平度幅值阈值为0.178 m时车体振动相图
Melnikov方法从本质上说是一种一阶近似方法,在求解过程中,对系统参数有一些要求与限制,并且会有一定的误差产生。
