DAG-OpenMC在聚变中子学分析中的应用研究
2022-06-09仲港其陆玉东毛世峰叶民友
仲港其 徐 坤 陆玉东 毛世峰 叶民友
1(中国科学技术大学核科学技术学院 合肥 230026)
2(中国科学院等离子体物理研究所 合肥 230031)
聚变中子学分析对聚变堆的设计与建造、安全运行与维护具有重要意义。聚变中子学分析即应用中子学理论、输运计算程序以及核数据库研究中子与结构材料的相互作用,聚变中子由等离子体区域向外部扩散的过程中会与包层、偏滤器、真空室、超导磁体等部件的材料发生作用,生成中子、光子和电子等粒子,进而引发嬗变、活化以及辐照损伤等问题。目前,中子学分析主要有两种方法:确定论方法和概率论方法(蒙特卡罗方法)[1]。由于托卡马克模型的复杂性,聚变中子学分析采用的主要模拟方法是蒙特卡罗方法与程序,其中应用最广泛的是美国洛斯阿拉莫斯国家实验室(Los Alamos National Laboratory,LANL)开发的三维蒙特卡罗程序MCNP(Monte Carlo N Particle Transport Code)[2],国内外相关研究机构也开展了其他三维蒙特卡罗程序的应用研究,如Serpent[3-4]、Tripoli[5]、Geant4[6]和OpenMC等。OpenMC是麻省理工学院于2011年开始开发的面向现代化计算机集群并行高效计算的开源蒙特卡罗粒子输运软件,采用高性能的并行算法,提高了并行扩展性,减少了进程通信时间,计算效率更为高效[7]。英 国 原 子 能 管 理 局(UK Atomic Energy Authority,UKAEA)、德国卡尔斯鲁厄理工学院(Karlsruhe Institute of Technology,KIT)以及威斯康星大学麦迪逊分校等研究机构不断推进OpenMC在聚变中子学分析中的应用研究,包括三维CAD建模功能、减方差方法的应用以及基准测试等[8-9]。KIT的研究人员在OpenMC中添加了McDeLicious计算代码,并且基于IFMIF-DONES装置模型对比了OpenMC-McDeLicious与MCNP-McDeLicious计 算结果,获得了良好的一致性结果[10]。由于聚变堆工程模型极其复杂,使用传统的构造实体几何(Constructive Solid Geometry,CSG)方法建模十分繁琐和耗时,目前主要有两种方式解决该问题:CAD模型到CSG模型的转换,典型的模型转换程序包括CMGC[11]和McCAD[12]等;直接基于CAD模型进行粒子输运模拟。DAGMC(Direct Accelerated Geometry Monte Carlo)是威斯康星大学麦迪逊分校开发的开源工具包,通过在蒙特卡罗软件中插入核心几何库,实现了基于CAD模型的直接粒子输运模拟[13],避免了通过构造实体几何方法建模。DAGMC已经被集成到多个蒙特卡罗程序中,如DAG-MCNP、DAG-Geant4和DAG-OpenMC等。DAG-OpenMC继承了DAGMC与OpenMC的优点:基于CAD建模并直接在CAD模型上执行粒子输运模拟;高性能并行计算。这些优点在复杂聚变工程中子学分析中具有极大优势,被认为是解决聚变中子学分析问题的潜在方法。威斯康辛大学的相关人员通过耦合DAG-OpenMC与PyNE R2S,对FNGITER停堆剂量率基准题展开测试,通过对比MCNP、DAG-OpenMC以及实验结果证明了DAGOpenMC和PyNE R2S耦合可以有效计算聚变系统的停堆剂量率[14]。由于聚变装置工程模型非常复杂,建模十分烦琐和耗时,并且等离子体区域中子源的空间分布极其复杂,难以准确定义。针对上述问题,本文开展了OpenMC在聚变堆中子学工程分析中的应用研究,探究了OpenMC在复杂工程结构条件下的聚变中子学分析中的准确性与适用性。
中国聚变工程试验堆(China Fusion Engineering Test Reactor,CFETR)是中国磁约束聚变能计划的下一步试验装置,旨在为未来建造的示范堆提供参考[15]。本文首先基于CFETR一维柱壳中子学模型验证了OpenMC与MCNP程序关于聚变中子学典型物理量计算结果的一致性,表明了OpenMC可以准确计算聚变中子学物理量。进一步探究了DAG-OpenMC基于CAD建立复杂聚变堆工程模型的功能;基于平衡等离子体密度和温度分布计算得到等离子体中子辐射系数矩阵,根据该系数矩阵编写C++源文件定义CFETR三维中子学分析模型的D-T中子源分布,解决了OpenMC自带的源定义功能无法描述复杂的聚变中子源分布问题。将DAG-OpenMC应用于CFETR三维中子学模型,计算得到了中子壁负载分布、包层氚增殖率以及核热沉积等。
1 方法
1.1 基于CAD建模
DAGMC采用实体建模软件Trelis作为前处理模块,实现对CAD模型的预处理并转化为面网格模型。基于Trelis预处理模型的过程如图1所示,首先利用建模软件(如CATIA)创建托卡马克的复杂CAD模型,然后利用SpaceClaim对CAD模型进行简化,简化后将模型导入Trelis进行预处理。DAGOpenMC在粒子输运过程中执行严格的模型检查,即模型不允许出现几何干涉,因此要在Trelis中进行检测并修复模型。模型检测通过后,对模型所有表面进行“压印”(Imprint),确保面的准确定义。表面“压印”成功后,合并模型并再次检测模型,此时检测几何干涉和表面重叠。重复上述步骤直至Trelis对模型预处理成功,即模型不存在任何错误。

图1 DAGMC建模过程[16]Fig.1 Modeling process of DAGMC[16]
模型预处理结束后,利用Svalinn提供的插件[17]在Trelis程序中为模型的几何表面赋予边界条件以及为几何体赋予材料属性,设定粒子输运边界限制粒子运动区域。在Trelis中处理好模型后,导出为dagmc.h5m文件作为OpenMC程序的几何输入。
1.2 等离子体源
托卡马克装置中复杂的等离子体物理,决定了中子源的复杂空间分布。MCNP采用Fortran source subroutine或者复杂sdef定义的格式,实现了复杂中子源的准确定义。而OpenMC提供的源定义功能较弱,在Fixed source运行模式下,仅支持定义点源、环形线源、球形源和立方体源。为了改善这一情况以及更精确的定义等离子体源,本文基于OpenMC的自定义源扩展接口,编写C++源文件定义复杂的聚变中子源。源文件中包含一个自定义的源类和在该类中生成源中子的函数,在该函数中定义源中子的空间分布、权重、方向和能量等信息,随后编译成动态链接库,在OpenMC程序运行时抽样源中子。
2 基于CFETR一维柱壳模型的聚变中子学参数计算与对比
在中子学分析中,常采用一维模型为装置的尺寸设计提供指导和优化。本节基于CFETR一维柱壳模型,选用MCNP5作为对比程序验证OpenMC在聚变中子学分析中的计算准确性,其中,MCNP版本为5.1.60,OpenMC版本为12.1。对比计算中,采用的中子截面库均为FENDL3.1d[18],该截面库从ACE格式转换为HDF5格式供OpenMC使用。OpenMC与MCNP模拟的粒子数量均为1×108个。CFETR功率为200 MW,其中聚变中子功率为160 MW,计算得出单位时间产生的中子数为7.11×1019。对比参数包括各部件中子通量与光子通量,包层中子能谱分布与光子能谱分布,核热沉积以及包层氚增殖率等。
2.1 CFETR一维柱壳模型
CFETR一维柱壳模型是一个多层同心圆柱体,径向上以多层圆柱壳结构表示CFETR中平面处径向各部件,以等离子体区域为界分为内侧和外侧两部分,上下平面设为反射面,中子学模型如图2所示。高场侧从等离子体区域至中心螺线管之间的结构分别为:第一壁钨铠甲、第一壁、增殖包层、氦气分配管组、屏蔽包层、真空室、冷屏、环向场线圈和中心螺线管;低场侧从等离子体区域至中心螺线管之间的结构分别为:第一壁钨铠甲、第一壁、增殖包层、氦气分配管组、屏蔽包层、真空室、冷屏、环向场线圈、杜瓦和生物屏蔽墙。各部件使用均质材料填充。各向同性的中子源均匀分布在等离子体区域内,能量分布遵从Gauss聚变谱分布,平均能量为14.079 1 MeV。
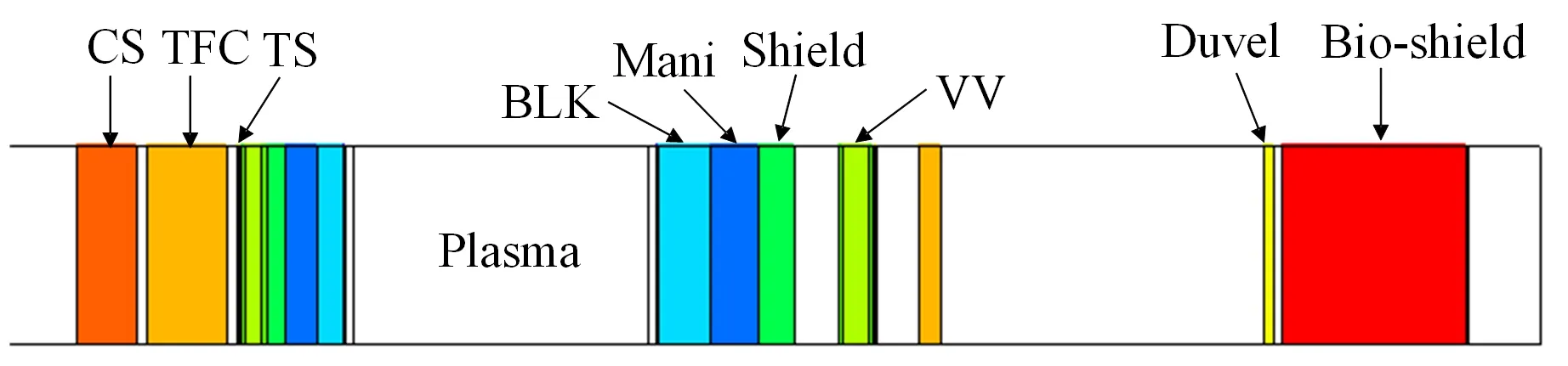
图2 CFETR一维中子学模型Fig.2 One dimensional neutronics model of CFETR
2.2 结果对比与分析
基于CFETR一维柱壳模型计算得到了在不同位置处的中子通量和光子通量(图3)。OpenMC与MCNP计算的第一壁、包层、屏蔽层以及真空室等靠近等离子体区域的中子通量与光子通量偏差不超过0.1%,具备良好的一致性。表明即使OpenMC处理光子输运时模拟的物理过程相较于MCNP存在部分不同,OpenMC的光子截面库相比于MCNP额外包含Geant4 EMLOW数据库中的Seltzer和Berger的轫致辐射截面、NIST ESTAR数据库的平均激发能量以及Biggs等计算的康普顿截面数据[19],但对结果并无太大影响。冷屏之外离等离子体较远的区域,中子通量与光子通量偏差较大,可达5%左右,但偏差基本不超过两倍OpenMC的统计误差(2σ),推测是通量统计误差造成的。
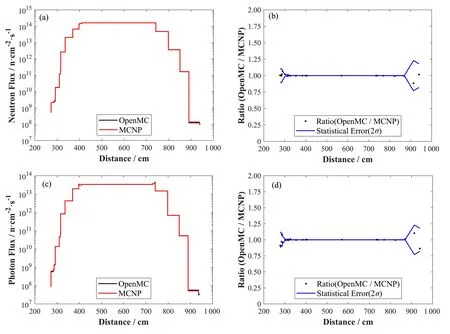
图3 中子通量(a)和OpenMC/MCNP中子通量比率(b),光子通量(c)和OpenMC/MCNP光子通量比率(d)Fig.3 Neutron flux(a)and OpenMC/MCNP neutron flux ratio(b),photon flux(c)and OpenMC/MCNP photon flux ratio(d)
聚变堆的核热沉积是等离子体产生的中子能量沉积和光子能量沉积的总和。中子核热沉积和光子核热沉积如图4所示,在不同位置处的OpenMC/MCNP核热沉积比值呈现了与通量比值相似的情况,第一壁、包层、屏蔽层以及真空室等靠近等离子体的区域核热沉积偏差基本不超过1%,冷屏之外离等离子体较远的区域核热沉积的偏差达5%~10%,但基本不超过两倍OpenMC的统计误差(2σ)。MCNP计算的总核热为217.214 MW,其中中子总核热为160.839 MW,光子总核热为56.375 MW;OpenMC计算的总核热为217.208 MW,其中中子总核热为160.717 MW,光子总核热为56.490 MW,OpenMC计算的中子总核热相较于MCNP低0.076%,光子总核热相较于MCNP则高0.204%,最终的总核热相较于MCNP低0.002%。总体来说,OpenMC与MCNP的计算结果一致。
中子能谱和光子能谱分析选取低场侧包层,能群划分选择Vitamin-j结构,该结构中子能谱的统计范围为10-7~20 MeV,共175个能量箱,光子能谱的统计范围为10-2~20 MeV,共125个能量箱。计算得到了OpenMC与MCNP的中子能谱图及光子能谱图(图5)。当中子能量大于10-5MeV时,OpenMC与MCNP计算出的中子通量偏差不超过1%。当中子能量低于10-5MeV时,OpenMC与MCNP的中子通量偏差变大,可达5%左右,但仍不超过两倍的OpenMC统计误差(2σ)。当光子能量位于10-2~10 MeV范围内时,OpenMC与MCNP计算出的光子通量偏差不超过1%。当光子能量高于10 MeV时,光子通量偏差变大,达5%左右,但基本不超过两倍的OpenMC统计误差(2σ)。
氚增殖率(Tritium Breeding Ratio,TBR)是衡量聚变堆包层氚增殖能力的参数,表示单位时间内包层中产生的氚原子数与等离子体中产生的聚变中子数的比值[20]。在CFETR中,主要产氚核素为6Li,同时,7Li和9Be也可产生极少量的氚。使用OpenMC与MCNP分别计算了6Li、7Li和9Be核素的氚增殖率,结果如表1所示。对于这三种核素,OpenMC计算的氚增殖率略低于MCNP。OpenMC的总氚增殖率为1.147 7,相较于MCNP的1.152 1低0.38%。总的来说,在计算氚增殖率时,OpenMC和MCNP的计算结果一致。

表1 OpenMC与MCNP包层6Li、7Li和9Be的TBR对比Table 1 Comparison of TBR of6Li,7Li and9Be between OpenMC and MCNP
总体来说,CFETR一维柱壳模型对比分析的结果表明OpenMC在中子学分析计算(包括通量、核热、能谱及TBR等)方面与MCNP一致,因此,OpenMC可以应用于聚变中子学分析。
3 面向CFETR工程模型的三维中子学分析应用
CFETR工程结构十分复杂,相较于一维柱壳模型,三维模型建模更加困难和繁杂,因此,减少建模工程的工作量尤为重要,而DAG-OpenMC的CAD几何功能在处理聚变堆复杂模型时可以显著提高建模效率,减少模型错误。聚变中子源对计算结果的可靠性具有直接影响,因此,在三维中子学分析中,使用符合实际情况的中子源来提高计算的准确性。
3.1 CFETR建模及中子源
CFETR第二阶段的设计大半径R=7.2 m,小半径a=2.2 m。主机由16个扇段组成,每个扇段包括2个内包层段和3个外包层段。典型的CFETR主机模型包括包层、真空室、偏滤器、冷屏、超导纵场线圈、中心螺线管和极向场线圈等部件。氦冷陶瓷增殖 包 层(Helium Cooled Ceramic Breeder blanket,HCCB)是CFETR的候选包层概念之一,该包层概念由核工业西南物理研究院提出,采用多模块化设计方式,在极向上分布有11个包层模块,内包层有6块(1#~6#),外包层有5块(7#~11#)。HCCB包层选用6Li富集度为90%的Li4SiO4小球作为氚增殖剂,金属Be小球作为中子倍增剂,Li4SiO4小球和Be小球以球床填充的方式交替分区布置在包层中[21]。HCCB包层单个扇段的布局和外侧中平面处增殖包层模块分别如图6(a)和(b)所示。考虑到CFETR模型的对称性,进行三维中子学分析时,在环向方向上选取11.25°的扇区作为分析模型,并采用反射边界条件模拟360°全堆模型。图7展示了CFETR HCCB包层的中子学计算模型。
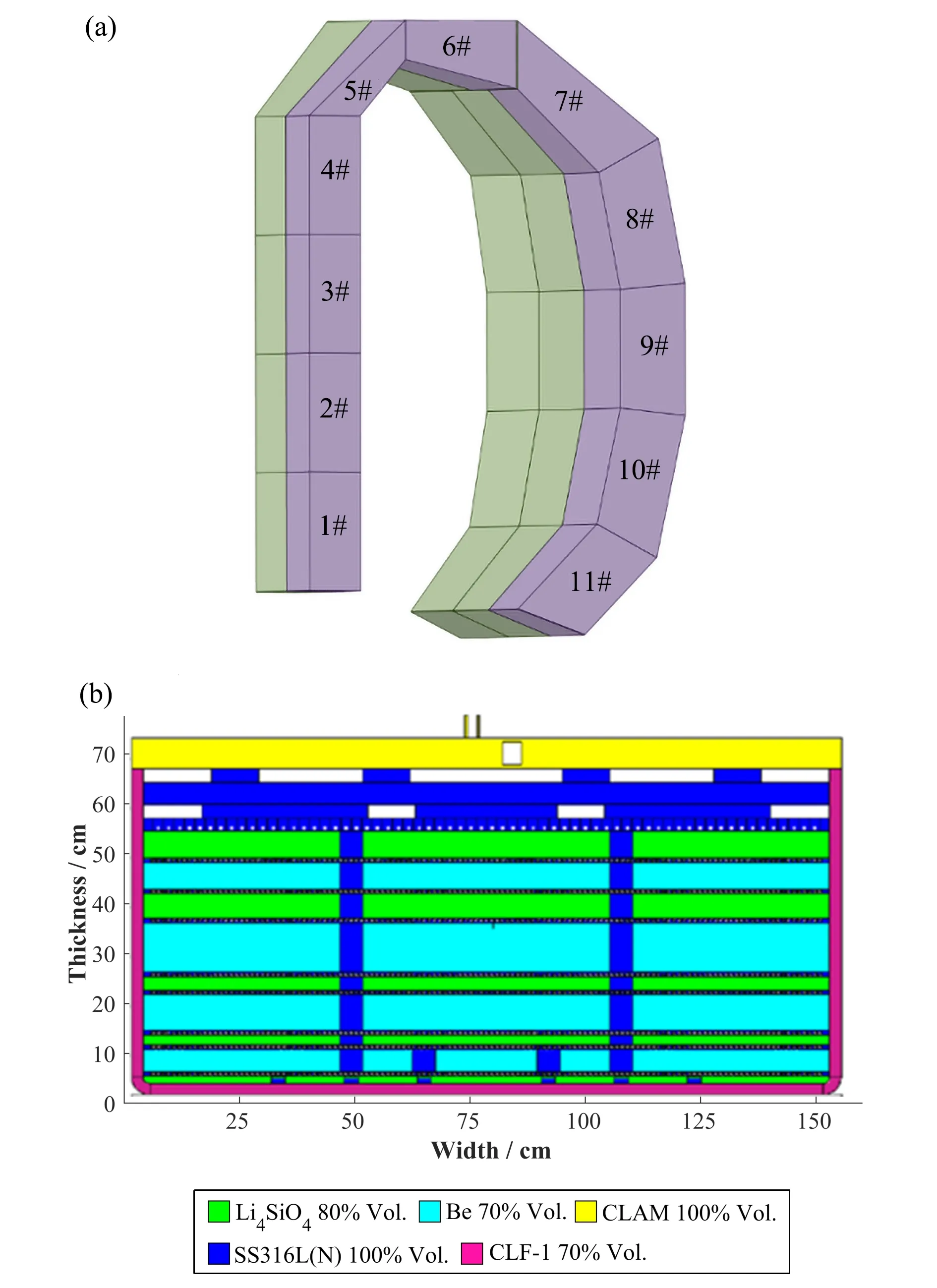
图6 单个扇段包层模块分布(a)和外侧中平面包层模块(b)Fig.6 Module distribution of single sector blanket(a)and outer mid-plane blanket module(b)

图7 CFETR中子学模型的纵向剖面(a)和内、外侧结构的水平剖面(b)Fig.7 Vertical cross section(a)and horizontal cross section of the CFETR neutronics model(b)
托卡马克装置发生D-T聚变反应产生的中子平均能量为14.079 1 MeV,遵从Gauss聚变谱分布。空间分布大致呈D形,等离子体中心中子源密度最高,并向等离子体的边缘逐渐减少。基于平衡等离子体密度和温度分布计算得到CFETR等离子体中子辐射系数矩阵[22],根据该系数矩阵以及参考MCNP网格离散体源的定义方式,将中子源离散成多个各向同性的体源,每个体源权重不同,在同一体源内源中子均匀抽样。基于OpenMC提供的源扩展接口,使用C++实现了二维(R-Z)各向同性的40×40网格离散体源来描述CFETR模型中D-T中子源的空间分布,并将结果与MCNP-sdef定义的中子源作对比,如图8所示。可以发现,两者定义的中子源在空间分布上具有极好的一致性(在等离子体边缘区域,源概率低于10-8,抽样统计误差较大,导致两者空间分布在此处存在偏差)。
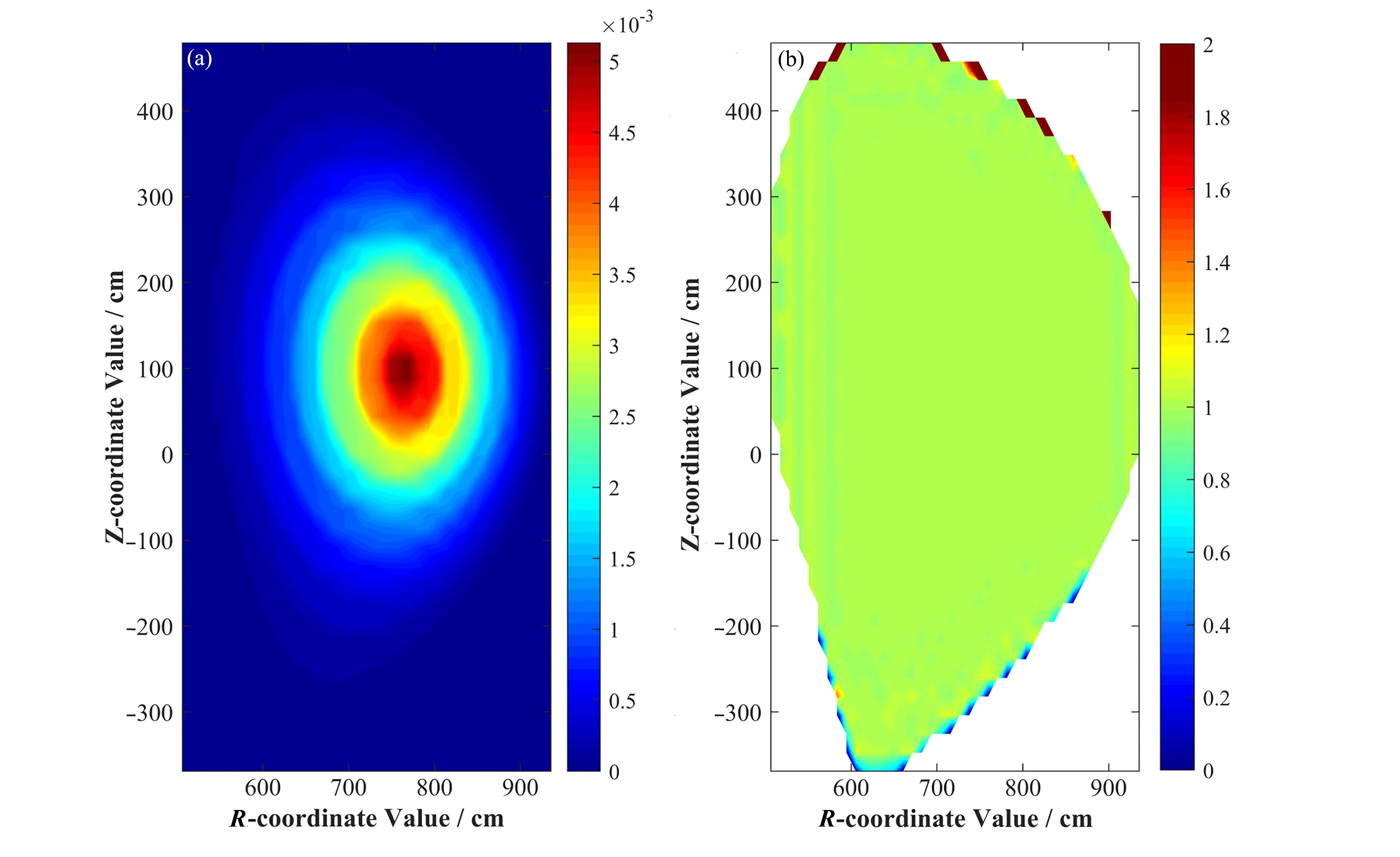
图8 中子源空间分布(a)和OpenMC与MCNP的中子源空间分布概率比值(b)Fig.8 Spatial distribution of neutron sources(a)and Probability ratio of neutron source spatial distribution between OpenMC and MCNP(b)
3.2 中子壁负载分布
中子壁负载指的是托卡马克装置中D-T聚变反应生成的14.08 MeV的中子直接作用到第一壁表面的中子能量通量密度。包层中子第一壁总负载约为144.4 MW,占160 MW聚变中子功率的90.25%。图9为各个包层模块的中子壁负载分布,内包层中子壁负载峰值出现在3#包层,达到0.156 6 MW‧m-2,外包层中子壁负载峰值出现在9#包层上,达到0.227 1 MW‧m-2,中 子 壁 负 载 的 平 均 值 为0.169 4 MW‧m-2。

图9 中子壁负载分布Fig.9 Neutron wall load distribution
3.3 包层氚增殖率
计算得到了HCCB包层中各包层模块在200 MW聚变功率下对氚增殖率的贡献(图10)。包层总TBR为1.141,其中外包层总TBR为0.798,内包层总TBR为0.343。

图10 各包层模块对TBR的贡献Fig.10 Contribution of each blanket module to TBR
3.4 核热沉积
聚变堆的核热沉积由中子核热沉积和光子核热沉积组成,全局能量倍增因子是全堆核热总功率与聚变中子功率的比值[23],是评估聚变堆核热产出能力的重要参数之一。
表2列出了CFETR各部件的核热沉积和占比情况,全堆产生的核热共计211.73 MW,全局能量倍增因子为1.32。其中包层系统产生的核热达185.64 MW,占总核热的主要部分(占比87.68%),偏滤器产生的核热为24.98 MW,占比11.80%。
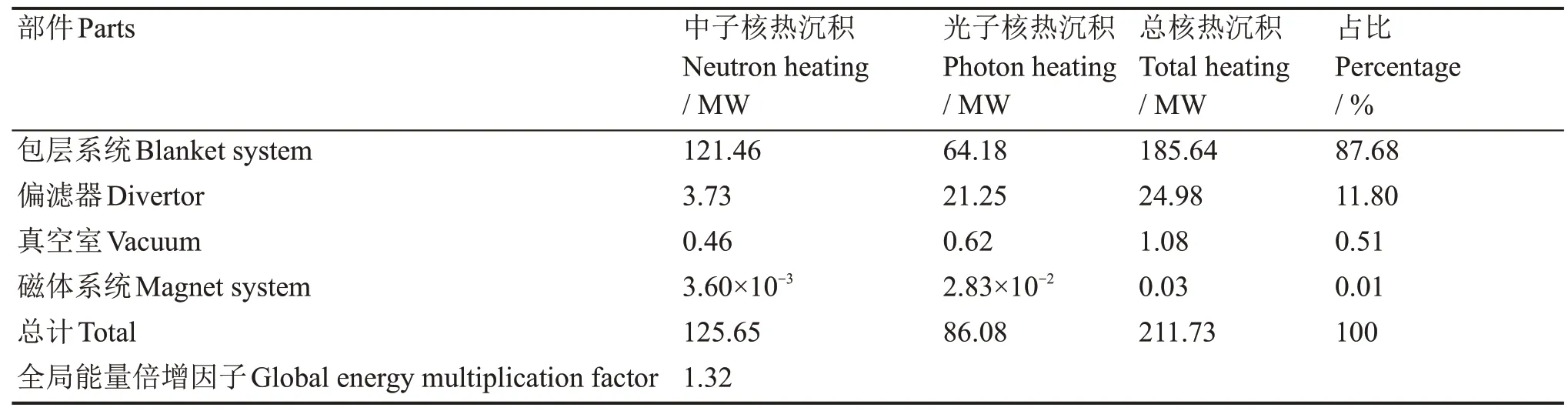
表2 CFETR各部件核热沉积Table 2 Nuclear heating of CFETR components
4 结语
开源代码OpenMC为聚变中子学分析提供了一种选择,该程序易于获取和进行二次开发。本文基于CFETR一维柱壳模型对比分析了OpenMC与MCNP关于中子/光子通量、中子/光子核热沉积、中子/光子能谱以及包层氚增殖率等聚变中子学参数的计算结果,结果显示,OpenMC与MCNP在中子学分析计算方面具有良好的一致性,表明OpenMC可以应用于聚变中子学分析。
在CFETR的三维中子学分析中,使用实体建模软件Trelis对三维CFETR的CAD模型进行预处理,集成DAGMC实现OpenMC在该模型上直接进行粒子输运模拟,实现了DAG-OpenMC中聚变堆的建模。基于计算得到的等离子体中子辐射系数矩阵,参考MCNP网格离散体源的定义方式,编写C++源文件在OpenMC中实现了精确的D-T聚变中子源定义。因此,在聚变堆复杂工程结构条件下,DAGOpenMC在建模及设置中子源方面均满足要求。经计算,CFETR中子壁负载峰值出现在中平面处,氦冷陶瓷增殖包层TBR为1.141。在聚变中子功率为160 MW时,产生的总核热为211.73 MW,全局能量倍增因子为1.32,其中包层产生的总核热为185.64 MW,占总核热的87.68%。
作者贡献声明仲港其:实施研究,采集数据,分析/解释数据,起草文章;徐坤:指导,统计分析,技术及软件支持,对文章的知识型内容作批评性审阅;陆玉东:采集数据;毛世峰:指导,支持性贡献;叶民友:指导,对文章的知识型内容作批评性审阅。
