装甲车辆履带板疲劳寿命预测
2022-06-09白恩军黄树涛
韩 尧,白恩军,黄树涛,杨 慧
(沈阳理工大学 汽车与交通学院,沈阳 110159)
履带式装甲车辆通过履带推进装置可在极为复杂的环境中行驶。履带板作为整车与地面直接接触的零件,接收驱动轮传来的驱动力并将其转化为牵引力传给地面,从而由地面反作用力带动车辆行进。由于履带式装甲车辆行驶路面多为砂石、沟壑、冰冻、松土等极差路面,加之受力情况不良,拉压、弯曲等应力都作用在履带板上,致履带板极易发生磨损,使其成为装甲车辆消耗量最大的零件之一[1-2]。因此,履带不仅要有良好的附着能力,还应具有足够的强度。为保障装甲车辆行驶时履带部分工作可靠性,必须对其进行疲劳寿命预测,防止在行进过程中承受负重轮压力或长时间工作产生严重磨损甚至疲劳断裂。马亚飞等[3]采用疲劳裂纹增长率的方法,根据等效初始裂纹尺寸对吊杆疲劳寿命进行了预测。Yamada K[4]深入研究十字焊接接头的疲劳寿命和可靠性,基于Paris公式进行裂纹模拟,以蒙特卡洛法给出了十字接头的裂纹尺寸形状及气孔大小等,这些特征由随机变量表示且模拟结果与实际相似,可作为相关研究的有效参考,也验证了蒙特卡洛法的可靠性。尚德广等[5]基于多轴疲劳损伤原理对多轴非线性连续疲劳损伤累积模型进行深入研究,提出的模型不仅考虑了多轴疲劳极限、平均静应力及损伤参数与加载参数的不可分割,还表达出多轴顺序对结果的影响,探讨此模型在多级加载条件下的递推形式,利用模型合理预测多轴的疲劳寿命。
本文以履带式装甲车辆为研究对象,通过虚拟样机技术构建装甲车辆三维模型,进行仿真分析得出所需载荷谱;再将履带板导入有限元分析软件进行静力分析,研究其在驱动力作用下的履带板受力情况;最后通过线性疲劳累计损伤法对履带板进行疲劳寿命预测,为履带车辆的可靠性研究提供参考依据。
1 整车动力学模型
本文以中型坦克的履带为模型原型进行数据采集,研究对象原型如图1所示,构建模型时进行简化,忽略非必要因素。本文研究的履带环包括90块履带板和90根履带销,履带板材料为ZGMn13,单块履带板的长度为5100mm,最宽处宽度为1700mm,高度为400mm,履带板连接处的销孔直径为30mm。
1.1 整车模型建立
拟定履带板相关参数,并对无影响细节进行简化设计,构建履带板三维模型。部分履带板(取履带板1/30)模型如图2所示。

图1 中型履带式装甲车辆

图2 部分履带板三维模型
构建履带式装甲车辆动力学模型,如图3所示。模型各部分经过简化处理,各部分的主要参数,如各部件尺寸、转动惯量、负重轮个数、履带板间距等,由文献[6]和实际测量获得;检查调整约束,保证机构合理运动;进行触发器和求解器设置,完善模型,为仿真做准备;剩余其它参数由系统自动生成,满足动力要求。

图3 履带式车辆整车模型
1.2 三维路面模型建立
根据对标准路面不平度系数的认定标准,一般将路面划分为A~H八个等级[7],如表1所示。
表1中:A为高速公路;B为沥青路;C为砂石路;D为未铺装路面和土路;E为未铺装路面的损坏路面和碎石路面;F为田野路面;G为未铺装的不平路面和被车辆碾压损坏的路面;H为崎岖山路;Gq(n0)为路面谱密度不平度系数;n0为参考空间频率,取0.1m-1;IRI为路面不平度。
根据ADAMS/ATV仿真软件进行三维路面模型的建立,主要基于Sayers经验模型,修改更换空间功率谱密度Ge、速度功率谱密度Gs、路面不平度IRI、加速度功率谱密度Ga等参数构建出不同类型的路面进行仿真分析[8]。
空间功率谱密度函数需转化为速度和加速度的功率谱密度函数,基于Sayers经验模型所构建的路面,满足以下公式[9]
(1)
式中:Gd(n)为路面轮廓的空间功率谱密度,m2/m-1;Ge为 空间功率谱密度幅值,m3;Gs为速度功率谱密度幅值,m;Ga为加速度功率谱密度幅值,m-1;n为空间频率,m-1。
对应Sayers经验模型中的路面类型随机输入路面的功率谱密度(Power Spectral Density,PSD)参数,如表2所示。
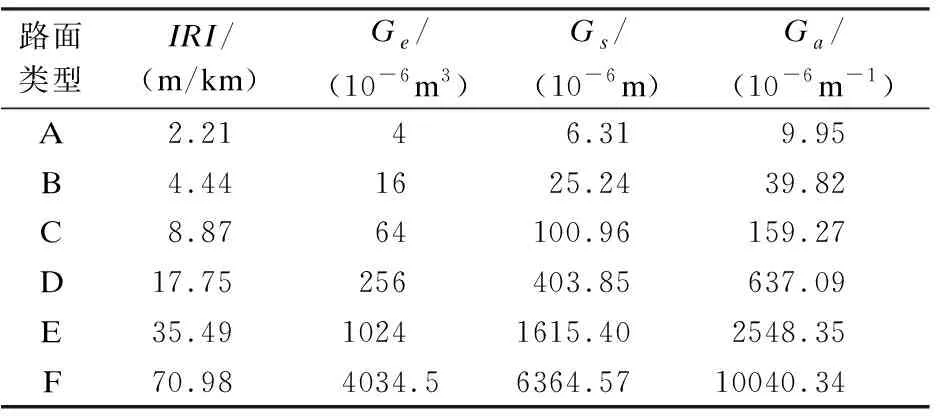
表2 功率谱密度(PSD)参数
建立符合实际的任务剖面后再对履带板疲劳寿命进行研究才能更加合理。通过设计履带式装甲车辆行驶路面分配百分比及行驶速度分配百分比,可以确定履带式车辆的任务剖面[10]。鉴于履带式装甲车辆复杂的工作环境,考虑行驶时加速、减速、制动及爬坡的情况,确定C、D、E三种路面作为试验路面。
1.3 实验设计
履带式装甲车辆标准实验里程为10000km,为简化实验时长,提高实验效率,同时最大限度还原履带式装甲车辆的真实行驶状况,对三种路面分别进行3500、3000、3500m模拟,然后按已建立任务剖面中所占的百分比叠加,得出10000km的目标载荷。最后通过载荷历程线性转换理论,获取应力谱。

表3 实验路面速度分配
2 履带板静力学有限元分析
2.1 网格划分
以三块履带板、两根履带销所组成的装配体为分析对象,采用四面体单元类型,平滑度选择中等;网格长度选取4mm。履带板结构较为复杂,选取自动划分,网格划分共计219206个节点,如图4所示。
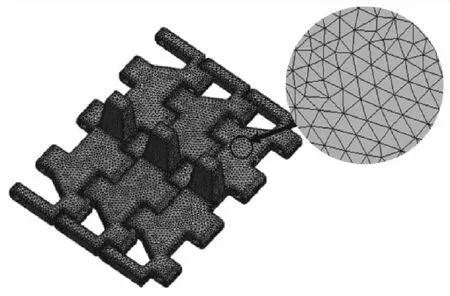
图4 履带板网格划分
2.2 履带板材料属性
履带板工作环境复杂,一般选用耐磨且韧性较好的ZGMn13材料铸造而成,该材料一般含碳量为1.00%~1.40%。在国内研究[11]中,新型履带板材料设计应取含碳量在0.60%~1.00%,同等情况下该含碳量材料性能更优越,尤其在遭受弱冲击时,高锰奥氏体得到很好的强化。
2.3 边界条件
装甲车辆行驶路面崎岖,履带板与地面接触点不稳定,难以确定受力位置,所以对构建的履带板三维模型合理简化十分必要。本研究中忽略平稳运行时惯性力带来的影响;以履带板销耳外侧作为场力的作用部位;销耳所受载荷视为均匀分布。
确定合力作用位置:通过研究某块履带板在受力时的载荷变化,观察其曲线图,了解幅值变化规律,以此推断该位置是否产生载荷分量,进而确定该履带板合力作用位置。本文研究的履带板在运行至负重轮下方时具有较大幅值,而其它位置幅值较小,由此推断合力中垂直方向(铅垂方向)的分力作用部位为履带与负重轮的接触表面。
约束条件:一块履带板与相邻两个履带板接触,受两个场力作用,但由于两个场力对应的载荷幅值分布相差很小,因此在履带销半圆柱面施加固定约束,其约束反力与该履带销另半圆柱面对应的场力作用效果一致。由此可知,履带板与地面接触面添加固定约束后,该约束反力忽略惯性力和构成平衡力系所需的补充力。
2.4 有限元分析结果
在履带板横向位置添加F1=50000N、F2=60000N的作用力,如图5、图6所示。
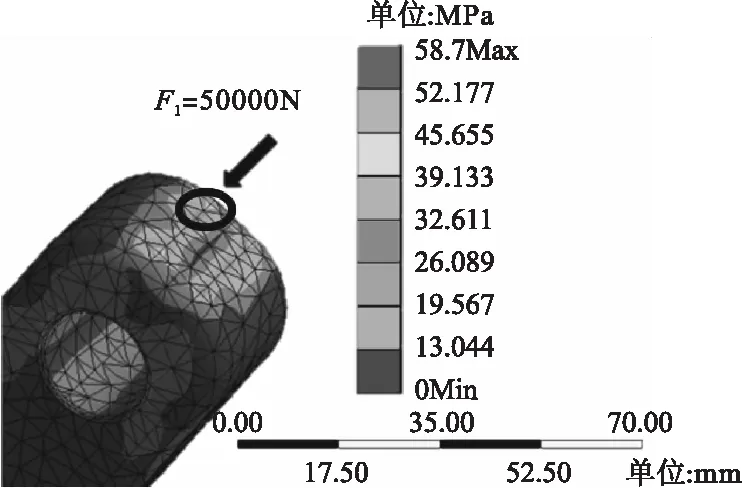
图5 横向力为50000N时的局部应力分布图
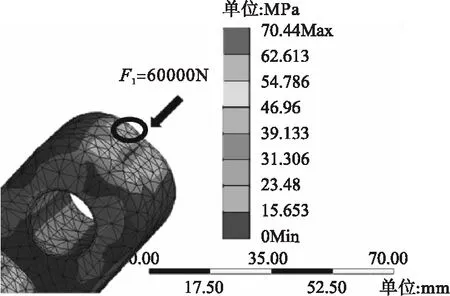
图6 横向力为60000N时的局部应力分布图
由图5、图6可知,履带板结构的危险点位于销耳内部靠孔边缘部分,此处达到应力最大值,分别为58.7MPa和70.44MPa。
3 履带板疲劳寿命
3.1 载荷历程线性转换
基于应力-强度干涉理论,可以计算得到履带板的疲劳可靠度,而履带在工作过程中的接触应力信息很难获得,但可以通过施加传感器的方式,测出横向载荷数据,对装甲车辆履带板进行仿真计算。通过对仿真结果的拟合分析,得知履带板的横向载荷与其应力间存在明显的线性关系,因此可以实现载荷与最大应力间的载荷历程转换。
通过更改横向载荷数值,得出不同等效应力结果,再计算得出载荷与应力的线性关系。将动力仿真软件所获取的数据带入,得到图7、图8、图9三种不同路面的等效应力数据。
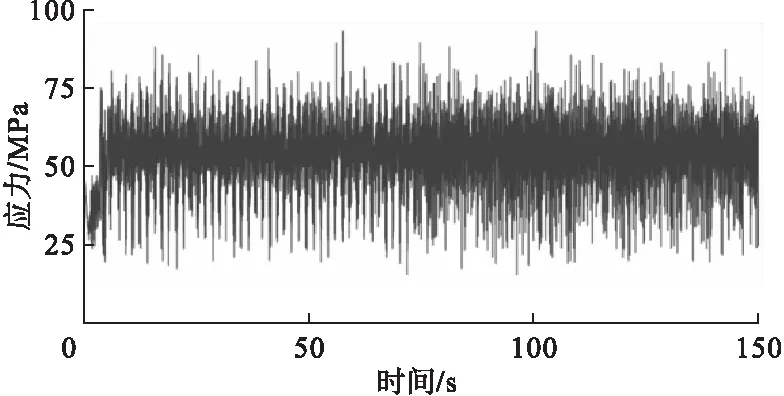
图7 C级路面应力谱
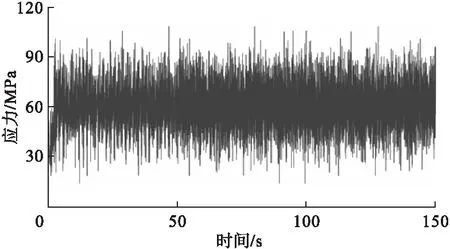
图8 D级路面应力谱
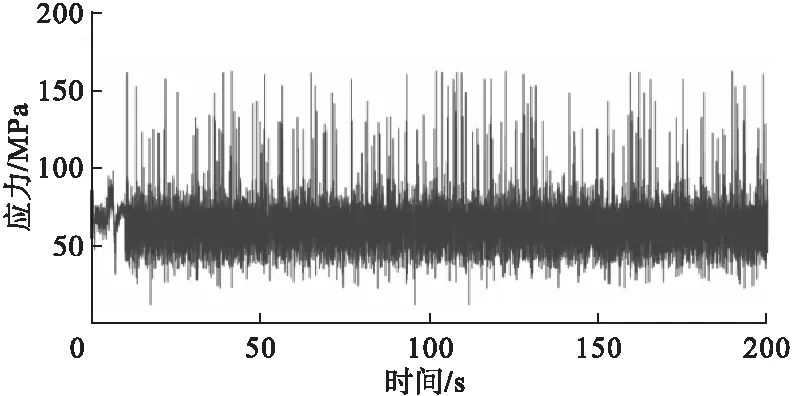
图9 E级路面应力谱
由图7~图9可以看出,C级和D级路面的载荷变化更加稳定,E级路面的载荷波动比较大。由此可知,在路面较为平坦时,对履带板的冲击较小,载荷变化幅度较小;在路面状况较差时,对履带板的冲击较大,载荷的变化幅度也更加明显。
在同一车速下稳定行驶,C级路面的车辆输出的牵引力最小;路况越差,需要的牵引力也越大。
3.2 履带疲劳寿命
机械零部件工作时承受的载荷与其疲劳寿命特性是抗疲劳寿命设计时需要重点研究的问题,载荷谱作为疲劳设计的基础数据,是履带疲劳寿命预测的前提。
通过对所获得的不同路况下的载荷谱进行雨流计数法[12]处理,获取其均值幅值。评价和预测零件的疲劳寿命,需建立材料在外部加载时应力幅值与疲劳寿命间的联系,一般由S-N曲线表示,该曲线明确给出应力σ和材料疲劳寿命N之间的线性相关性,材料的S(lgσ)-N曲线对数表达式为
lgN=ap+bplgσ
(2)
式中:ap和bp为材料常数,可由最小二乘法拟合确定;N表示存活率为p时材料的疲劳寿命;σ为应力幅值,MPa。本文装甲车辆履带板材料为ZGMn13,由于疲劳寿命分散性较大,需要考虑存活率问题。查表整理该材料在常规三种存活率下S-N曲线材料常数[13],如表4所示。ZMn13的S-N曲线如图10所示。
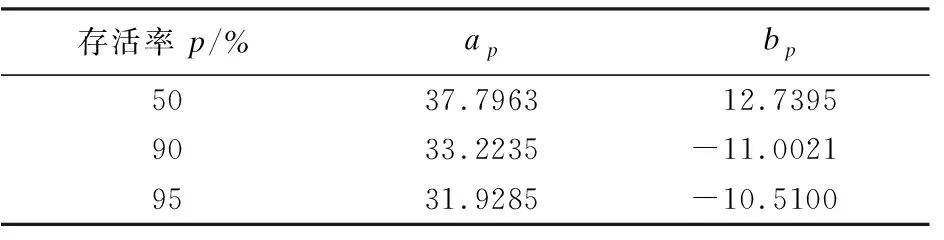
表4 三种存活率下材料常数
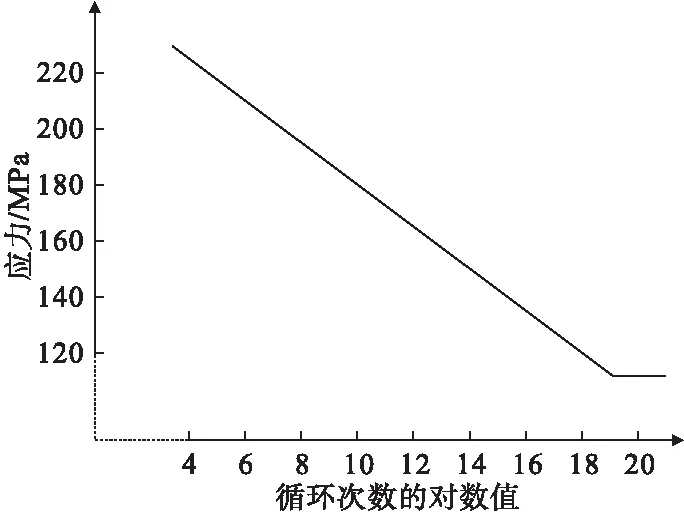
图10 ZGMn13的S-N曲线
实验中所研究材料的疲劳寿命受到来自材料本身力学性能的影响,同时也由外界施加的应力水平决定[14]。在履带式装甲车辆实际运行期间,由于履带板承载的外界载荷存在不确定性,即这些作用力可能是变幅且不对称,而平均应力对疲劳寿命有一定影响,所以必须对材料的特性曲线加以调整修正,修正后可极大减少疲劳寿命预测的工作量。本文采用Goodman法进行平均应力修正[15],即
(3)
式中:Sa为修正前的应力幅值;Sm为平均应力;Se为修正后默认均值为零的应力幅值;Su为材料抗拉强度。
将修正后的应力值带入式(2),根据疲劳损伤公式
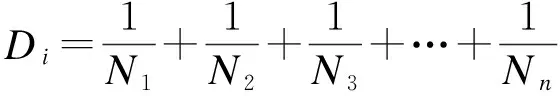
(4)
计算得到疲劳损伤Di,再根据线性叠加得到累积疲劳损伤D,公式为
(5)
三种存活率下,经过简单换算,疲劳寿命如表5所示。

表5 三种存活率下的疲劳寿命
由表5可知,同等存活率下,路面不平度越小,损伤量越小;在存活率为50%时,疲劳寿命最大;存活率越大,疲劳寿命计算结果越小。
4 结束语
利用虚拟样机技术进行路面仿真,模拟装甲车辆行驶状态,提取仿真结果中所需的履带板载荷历程,分析履带板载荷分量形成原因,以有限元法进行分析,求得此处应力应变变化关系;基于履带板载荷历程、该区域的应力分布情况和ZMn13的材料疲劳特性,计算求得履带板在不同存活率下特定路面的疲劳寿命。
根据本文的计算方法,通过对履带板的静力分析及疲劳寿命的分析和预测,可在产品开发阶段预测履带板的寿命;同时利用此估算疲劳寿命的方法,还可结合虚拟样机技术优化履带板结构,达到减少研制经费、缩短零件前期开发时间。
