基于Canopy的KFCM聚类优化算法
2022-06-09吴辰文梁雨欣
吴辰文,李 壮,梁雨欣
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
由于网络技术和计算机超强算力的发展,每天都有大量来自医疗、商业及生活方面的数据产生。如果只依靠手动的方式从如此量级的数据集中获取有效信息,其时间和人力成本是高昂的。因此,势必要借助现代化技术的计算能力。在众多对信息进行有效提取的方式中,聚类算法可以从海量级的数据中快速找到数据间的相关性,建立有用的数据模型。目前,使用频率高且典型的无监督算法有基于数据密度聚类算法(DBSCAN)、高斯混合模型最大期望聚类、凝聚层次聚类、模糊c均值聚类(fuzzy c-means clustering, FCM)和K均值聚类(K-means)。传统的聚类方法是在经典集合理论的基础上进行硬划分,即假设一个对象只属于一个聚类。但是在实际应用中,很多聚类问题在具体操作的过程中并没有特定的边界,无法将所有数据明确定义到一个具体的类别当中,因此,模糊聚类比硬聚类更自然。例如医疗的特殊领域,传统的硬聚类标准无法满足对基因和疾病样本聚类的需求。每个基因并不只拥有单一的功能和作用,可能同时担负多个任务。在药物治疗中,每种药物并不只局限于治疗一种疾病,而是对不同的疾病有不同的治疗效果。正是由于这些因素,使得模糊聚类与传统的硬聚类相比,更适用于药物和疾病基因的聚类。
所谓的模糊聚类是基于模糊集理论,使用数理统计的手段或方法对数据进行多元分析,通过数学方式定义样本间的强弱联系,再由联系的“强弱”对数据进行聚类。在具体的算法表达中,强弱是一个[0,1]的取值,用于表示属于某个类别程度的大小。在模糊聚类中,通过计算得到不同的隶属度值,使数据点可以在不同程度上属于多个标签。传统FCM使用欧氏距离,容易受到噪声和离群点干扰,为解决这个问题,有学者将FCM算法改进为KFCM(kernel fuzzy c-means clustering)[1],与FCM相比有更好的聚类性能。然而,KFCM算法依然存在一些问题:①在数据聚类过程中需要人为指定聚类个数,但由于现在的数据集体量过大,人为指定聚类个数不准确,会严重影响算法的聚类精度和性能;②聚类效果和精度容易被噪声数据点和环境因素影响。
1 相关工作
FCM算法由Dunn在1973年阐述并提出[2]。 2008年, 吕回等人为了优化并缓解FCM算法所存在的主要缺陷, 如数据初始化敏感, 且在进行聚类或运算时会出现局部最优解, 在FCM中加入了核函数的概念, 通过核把低维空间中不明显的特征突显出来, 得到更好的聚类效果[3]。2010年, 黄保海等人为解决聚类中高维数据非线性的缺陷, 提出以核主元分析(KPCA)为基础并结合KFCM集成的方法,利用核主元分析的优点直接对高维数据的特征进行筛选[4]。2013年靳璐等人针对红外图像的模糊聚类对初始中心敏感的问题,提出一种使用图像灰度进行分析然后聚类的遗传模糊核聚类算法,这个算法可以求解出全局最优聚类中心,并且计算得到其隶属度矩阵[5]。2015年,任昌荣提出一种使用多种群协同量子粒子群模拟退火(MCQPSO-SA)对KFCM进行优化,优化后的KFCM算法提高了局部和全局寻找最优解的能力[6]。2018年赵海峰等人重新设计了KFCM中的局部隶属度函数, 提出基于加权的模糊隶属度KFCM分割算法, 在提高算法鲁棒性的同时维持了算法的精度[7]。 2019年, 何云斌等人利用平均距离对KFCM进行优化, 其目的是解决算法对随机获取的聚类中心敏感的缺陷, 使KFCM算法能够自动获取比较优秀的聚类中心[8]。2021年Ciri等人提出了一种利用KFCM聚类的基于特征值的协作频谱感知(CSS)新技术,将信道分为可用和不可用两类,并在多维空间中提高了检测性能[9]。
本文在参考文献[2-3,8]的前提下,将KFCM与Canopy算法结合,使KFCM拥有自动确定聚类类别的能力。对KFCM的隶属度函数进行改进,将离群数据点和异常值数据点的数据隶属度由其最近邻的n个数据点的隶属度的均值来替换,使离群数据点和异常值数据点对KFCM算法的聚类性能和聚类效果的影响大大降低。
1.1 KFCM聚类算法
在FCM算法中引入一种基于核的相似性度量函数代替原先的欧氏距离[10],其中的核即为一种映射函数,将原数据集中无法通过一个线性函数划分的数据,通过数学方法变换到高维空间中,使其不显著但是有聚类意义的特征突显。这样不仅能够使算法处理线性不可分问题,还便于对聚类结果进行描述。
KFCM的目标函数公式为
(1)
其中:C∈[x,N)是数据的聚类总数;N是数据点的总数;uki是xi相对于vk的隶属度,且uki∈[0,1];φ表示高维度空间非线性特征映射。
1.2 Canopy算法
Canopy算法是Mccallum在2000年提出的粗聚类算法[11],Canopy算法通常可以作为其他无监督聚类算法之前的预处理,它能够在牺牲可接受程度内的精度对样本进行快速的聚类计算,作为辅助其他聚类算法的预处理[12]。Canopy算法使用距离将数据进行划分,并得到计算后的分类,再由后续聚类算法对数据进行处理[13]。Canopy算法与其他经典聚类算法结合可以对其他算法进行优化并缩短运行时间[14],也以用于直接聚类。在研究高维和大量的数据时,Canopy算法对数据分布情况以及确定样本的分组有极大价值[15]。
Canopy算法步骤如下:
Step1设置Canopy的距离阈值T1和T2,且T1>T2。
Step2在原始数据集中任取一点p,作为第一个聚类中心,并将其从原始数据集中删除。
Step3继续从原始数据集取点,计算其到所有已产生的聚类中心点的距离d。
1) 如果d 2) 如果T2 3) 如果d>T1,则该点成为新聚类中心点,并从原始数据集中删除。 Step4重复步骤3,直至原始数据集为空。 为解决KFCM算法需要手动输入聚类类别的问题,本文拟将Canopy快速粗聚类算法与KFCM算法相结合,使其自动确定聚类类别;其次,改进KFCM算法的隶属度函数[16],使其对类边缘点拥有更高的分类准确率,提高算法分类性能。 聚类算法的一个重要步骤就是如何确定一种可靠有效的衡量数据对象之间相似性[17]的计算方式。KFCM算法相似性度量方法采用核函数的形式,比如高斯核函数[18]、多项式核函数[19]和线性核函数[20]等,其公式定义如下。 线性核函数(linear kernel) k(x,y)=xTy+c。 (2) 其中:c为常数项;xTy为内积。 多项式核函数(polynomial kernel) k(x,y)=(γx·y+c)d。 (3) 高斯核函数(Gaussian kernel) (4) 其中:y为高斯核函数的中心;σ为高斯核的宽度参数,其大小由人工设置,并且控制函数在数据中的作用范围,过大或过小都会影响算法的性能。 而本文改进的KFCM算法是使用式(4)的高斯核函数。它对离群数据点和异常值数据点有着优秀的抗干扰能力,使算法更具鲁棒性。但缺点是函数在聚类和计算中的作用范围由其参数的大小决定,如果超出设定参数的最大范围,其核函数的作用就微乎其微,且函数对参数敏感,不容易达到预期效果。 在对式(1)进行求解后,得到矩阵中隶属度值和聚类簇心点的计算公式, (5) (6) 在KFCM中,核函数的本质[21]是进行非线性的变换φ:x→φ(x),就是将原算法距离公式‖x-y‖2以‖φ(x)-φ(y)‖2代替 ‖φ(x)-φ(y)‖2= (φ(x)-φ(y))T(φ(x)-φ(y))= φ(x)Tφ(x)-φ(x)Tφ(y)-φ(y)Tφ(x)+ φ(y)Tφ(y)。 (7) KFCM算法对数据进行聚类或者分类时,由于算法本身只看重数据的属性或特征,过于注重特征就会忽略局部数据间的相关性和数据与数据间隐藏的联系。而且KFCM算法的效率和性能又易受离群数据点和异常值数据点的影响。针对这些问题,本文对KFCM算法的隶属度函数进行改进。用任意数对空隶属度模糊矩阵U进行初始化,且数值范围为[0,1],使隶属度矩阵初始完成后满足以下要求, (8) 若算法判定一个数据点为噪声点,则使用该数据点邻域内的隶属度平均值进行计算, (9) 其中,E为噪声点i的邻域。 由于在K-means和KFCM聚类中,算法会将每个数据点分配到具体的簇类中,因此,本文提到的数据噪声点主要为聚类的边缘错分点,以解决类边缘数据点相互影响导致分类错误的问题。噪声点的判断方法为:取可能为噪声点数据最近邻的n个数据点,同时计算n个数据点的类型,若有n/2个数据点的类型与此点不同,则其为噪声点。对噪声点通过式(9)的隶属度函数进行计算后,可以使KFCM算法更具鲁棒性。 KFCM算法是一种以模糊集理论为基础并佐以数学分析手段的聚类算法。 模糊聚类从根本上讲是软聚类, 即每个数据样本都有对类别划分的概率, 且所有概率相加为1。 同时, 这些概率也会在计算时说明数据在给定聚类群中的存在程度。 与传统的硬聚类相比, 模糊聚类更能表达出数据的本质意义, 也能为后续的数据处理和数据挖掘给予更多有用的信息。 但KFCM算法仍需人工指定聚类个数且对噪声敏感。 为此, 本文将KFCM和Canopy算法相结合,提出C-KFCM算法。无需人工干预,由Canopy算法给出初始聚类个数作为KFCM算法的输入,防止人工干预的不确定性影响算法的效果和性能,提高KFCM算法的准确性。 C-KFCM算法步骤如下: Step1用Canopy粗聚类算法计算原始数据集聚类个数C和集群S。 Step2将C和S作为KFCM算法的初始输入,并设置模糊参数m、核函数条件σ、收敛边界值ε和迭代数t。 Step3使用[0,1]的随机数对隶属度矩阵进行初始操作,并使用式(5)计算隶属度矩阵。 Step4使用式(9)重新对隶属度矩阵中的噪声点进行计算。 Step5使用式(6)对数据的聚类中心进行计算。 Step6判断若|Cn-Cn-1|<ε,则算法收剑,结束算法,否则执行Step3。 实验条件:Windows 10,i5-4200M,4 GB,Python 3.6.2: Anaconda custom。为对本文提出的C-KFCM算法进行综合全面的评价,将数据集分为两大类,一类为真实数据集,另一类为人工合成数据集。使用这些数据集对算法的性能和聚类效果进行实验,数据集属性如表1所示。实验使用的人工合成数据集包括Spiral、Jain、D31、Isquare2和Aggregation,真实数据集包括Iris和Wine。 表1 实验数据集属性Tab.1 Experimental data set properties 为准确且全面地评价本文的C-KFCM算法,使用准确率(ACC)[22]和调整兰德系数(adjusted rand index,ARI)[23]对C-KFCM算法的聚类效果进行比较和分析。 聚类准确率(ACC)计算公式为 (10) 调整兰德系数(ARI)计算公式为 (11) 其中:U集合为数据的真实标签;V集合为聚类结果;a为在U集合和V集合中是相同簇类的数据对个数;b为在U集合中为同簇类的数据对,但在V集合中是异簇类的数据对个数;c为在U集合中属于异簇类的数据对,但在V集合中是同簇类的数据对个数;d为在U集合和V集合中都是异簇类的数据对个数。 ACC和ARI两种聚类指标皆为[0,1]的取值,且越接近1算法性能越高。 实验使用4个人工数据集对C-KFCM的聚类数量准确率进行评测,目的在于验证与粗聚类算法Canopy结合后的KFCM算法在识别数据集类别时,是否具有一定的准确率和稳定性。由于Canopy算法属于粗聚类算法,本身缺乏一定聚类的精度,因此,在结合后的算法中,采用运行一次C-KFCM算法,运行n次Canopy算法,获得n个聚类数量结果,再求取n次结果平均值的办法来提高准确性,n的取值为10。表2为C-KFCM算法的聚类类别数量结果。 通过图1对比每组平均集群数和数据真实集群数, 可以看出, 聚类数据的平均值大多都非常接近真实的集群数量, 且误差在±0.5以内。 再对聚类平均结果取整, 得到C-KFCM聚类数目。实验表明,Canopy和KFCM结合后的算法在获得真实集群数量上有一定的准确性和稳定性。 表2 C-KFCM算法聚类类别数量Tab.2 Clusters number of C-KFCM algorithm 图1 C-KFCM平均集群数与真实集群数对比Fig.1 C-KFCM average clusters number compared with actual clusters number 实验在4个人工数据集和两个真实数据集上进行,将C-KFCM算法和Canopy、K-means、DBSCAN和KFCM算法进行对比,评价聚类性能和效果。采用主成分分析法将数据集属性降至二维以便计算。其中,D31、Isquare2、Spiral和Aggregation人工数据集中,特征数量为2,但D31样本和类别较多且类边缘交叠,真实数据集Iris和Wine拥有多个特征属性。 聚类实验的效果如图2所示。对比6组可视化聚类实验分析可以得出,Canopy算法本身就属于粗聚类算法,聚类速度占有优势,但聚类精度却处于劣势。K-means算法由于对非凸数据集难以收敛且容易陷入局部最优,因此,对识别Spiral和Isquare2数据集的形状聚类能力较差。DBSCAN是对数据分布密度感知较强的算法,因此,对数据密度分布差异不大的数据聚类效果较好,如Aggregation、Spiral、Isquare2数据集。但由于此算法的内部参数ε需要手动调整,且对数据密度敏感,过大或过小都会导致聚类失败,在Iris和Wine数据集中聚类效果较差。对于KFCM算法,虽然通过核函数对其突显特征在高维空间进行聚类,但由于对数据噪声敏感,且类边缘数据点相互影响,导致部分数据点分类错误,如在Aggreation和Wine数据集上的聚类效果。C-KFCM算法在所有聚类算法中表现出较好的稳定性和准确率,并能成功识别出数据的原有形状,且纠正了KFCM聚类错误的边缘点和错分点。 图2 5种算法对不同数据集的聚类结果Fig.2 The clustering results of five clustering algorithms on different dataset 综合实验结果对比聚类算法性能,由图3和图4可以看出,本文改进算法C-KFCM在准确率和调整兰德系数两种指标上均表现出比较优秀的聚类性能,与原KFCM算法相比聚类效果要更好一些。由于Canopy、K-means、DBSCAN和KFCM算法本身的侧重点不同,都存在各自的缺陷,因此,在特定数据集上表现不甚乐观。实验证明,本文改进的C-KFCM算法在大部分数据集都达到了比较优秀的聚类效果和较高的聚类准确率。 图3 ACC指标对比Fig.3 Comparison of ACC indicators 图4 ARI指标对比Fig.4 Comparison of ARI indicators 本文针对KFCM算法需要人工干预聚类簇数,且聚类效果不稳定的问题,提出C-KFCM算法。将KFCM算法与Canopy算法相结合,再改进算法的隶属度函数,将数据边缘点的隶属度由近邻点的平均隶属度代替,提高了算法的准确率和稳定性。通过与改进前的KFCM算法进行对比,纠正了KFCM算法在聚类时产生的少量噪声点和错分点,相较于原始算法准确率有所提升。同时,在与相关算法对比不难发现,C-KFCM在准确率方面对易分的数据集形状与对比算法基本没有差距,而在不规则形状的数据集上,准确率要优于对比算法。但C-KFCM依然存在不足,获取聚类集群数量是通过迭代求取平均值的方式,这在面对大规模数据集时无疑会付出巨大的时间和算力消耗,因此,如何优化算法自动集群,降低算法的复杂度和性能消耗是接下来的研究重点。2 算法改进
2.1 相似性度量方法
2.2 改进KFCM的隶属度函数
2.3 Canopy算法与KFCM算法相结合的C-KFCM算法
3 实验结果与分析
3.1 实验介绍

3.2 聚类评价指标
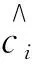
3.3 C-KFCM聚类类别分析

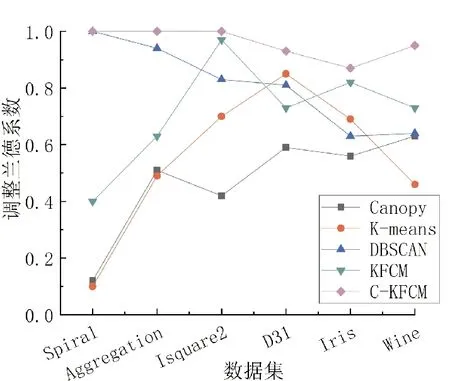
3.4 C-KFCM与KFCM准确率分析
4 结语
