广义Mycielski图Mn(Pt)的邻点可区别的I-均匀全染色
2022-06-08张修雪赵慧霞
张 婷,张修雪,王 昕,赵慧霞
(1.兰州文理学院 教育学院, 甘肃 兰州 730010 2.兰州文理学院 学报编辑部, 甘肃 兰州 730010)
图的染色问题是图论中的一个经典而古老的问题,也是图论领域的一个重要研究方向.目前,图的染色问题已由传统的点染色、边染色、全染色拓展为各类具有复杂特征的新型染色问题,图的均匀染色就是其中之一.图的均匀染色强调了任意两个色类所染元素个数最大相差为1,它常用来解决一些分配、调度及负载平衡问题.1973年, Meyer[1]最早提出了均匀染色的概念;1994年, Fu H[2]在《Some results on equalized total coloring》中提出了均匀全染色概念及均匀全染色猜想.近年来, 许多学者围绕图的各类均匀全染色做了大量研究[3-8].文献[4]提出了邻点可区别I-全染色的概念.文献[5]给出了邻点可区别I-均匀全染色的概念和邻点可区别I-均匀全染色猜想.文献[10]给出了若干Mycielski图的邻点可区别I-均匀全染色.本文根据路的第一类广义Mycielski图的构造特征,运用函数构造法研究并确立了这类图邻点可区别I-均匀全色数.特别的,当t>3时,针对路的第一类广义Mycielski图Mn(Pt),根据n的取值分5种情况讨论并给出了其邻点可区别的I-均匀全色数, 所得结果验证了这类图满足邻点可区别I-均匀全染色猜想:
1 基本概念和引理
定义1[4]对于阶数不小于2的连通图G(V,E),设f是从V(G)∪E(G)到{1,2,…,k}的映射,k为自然数,如果f满足
(1)对∀uv∈E(G),u≠v,有f(u)≠f(v);
(2)对∀uv,uw∈E(G),v≠w,f(uv)≠f(uw);
(3)对∀uv∈E(G),u≠v,C(u)≠C(v),
则称f为G的一个邻点可区别的I-全染色(简记为k-I-AVDTC).

定义2[5]设f是简单连通图G(V,E)
(|V(G)|≥2)的一个k-I-AVDTC,若满足∀i,j∈{1,2,…,k},i≠j,有
||Ti|-|Tj||≤1,

Ti=Vi∪Ei,
Vi={v|v∈V(G),f(v)=i},
Ei={e|e∈E(G),f(e)=i}.
定义3[11-12]对简单图G(V,E),|V(G)|=p,n是自然数,Mn(G)称为G的第一类广义Mycielski图,如果
V(Mn(G))=
{v01,v02,…,v0p;v11,v12,…,
v1p;…;vn1,vn2,…,vnp};
E(Mn(G))=
E(G)∪{vijvi+1,k|v0jv0k∈E(G),
1≤j,k≤p,i=0,1,…,n-1}.

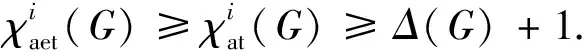
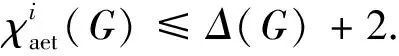

2 主要结果与证明
定理1设P3为3阶路图,则
证明当t=3时,图Mn(P3)中没有相邻的最大度点,且Δ(Mn(P3))=4.根据引理1,有
为证定理为真,只需给出图Mn(P3)的一个4-I-AVDETC.为此构造映射f:V(Mn(P3))∪E(Mn(P3))→{0,1,2,3},令f为
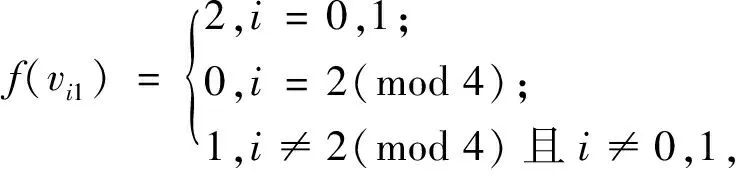
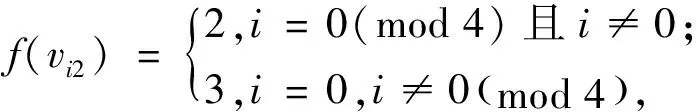
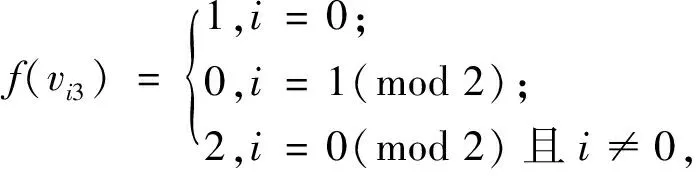
f(v01v02)=0,f(v02v03)=1,
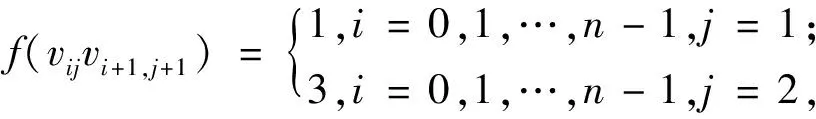

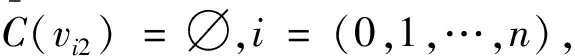
当n=0(mod 4)时,有
当n=1(mod 4)时,有
当n=2(mod 4)时,有
当n=3(mod 4)时,有
综上,由定义2可知,f是图Mn(P3)的一个4-I-AVDETC.
定理2设Pt为t(t>3)阶路图,则
证明当t>3时,图Mn(Pt)中有相邻的最大度点,且Δ(Mn(Pt))=4.根据引理1,有
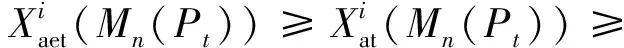
Δ(Mn(Pt))+1=5.
情形1当n=0(mod 5)时,令f为
f(v01)=1,f(v02)=2,f(v03)=4,
f(v0j)=

f(v3j)=
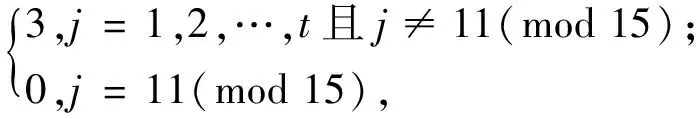
f(vij)=
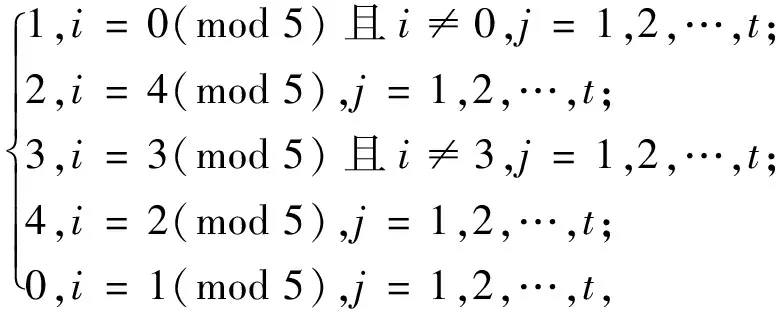
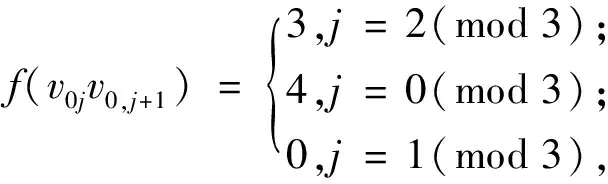
f(vijvi+1,j+1)=
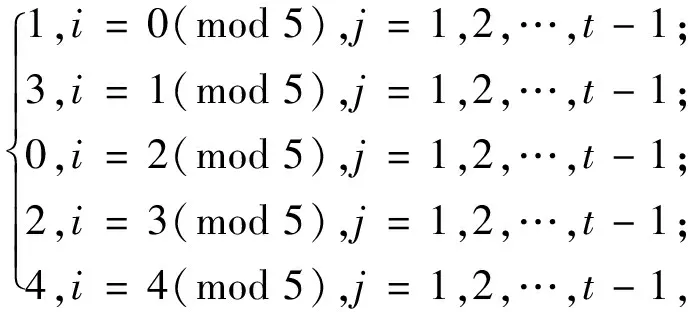
f(vijvi-1,j+1)=
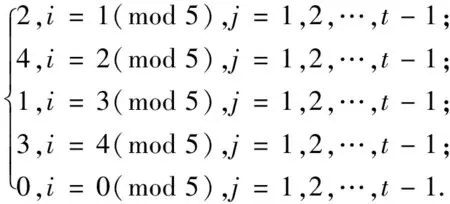
为验证上述染色方法f是邻点可区别的,下面给出各顶点的色集合:
由于顶点vi1(i=0,1,…,n),vnj(j=1,2,…,t),vit(i=0,1,…,n)的度均为2,顶点vn1,vnt的度均为1,而与这些点相邻的顶点的度均为4,故这些点的色集合显然与其相邻顶点的色集合不同,因此无需再进一步验证.综上所述,此染色法f为邻点可区别的,且各种颜色所染元素数为
从而由定义1可知,f是图Mn(Pt)当n=0(mod 5)时的一个5-I-AVDETC.
情形2当n=1(mod 5)时,令f为
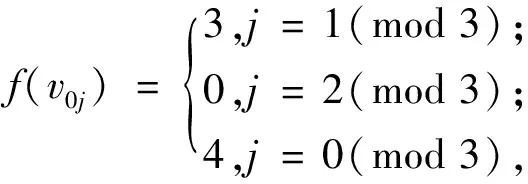
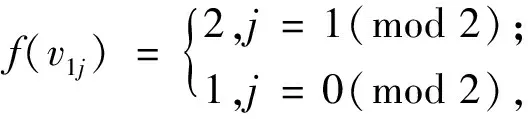
f(vij)=
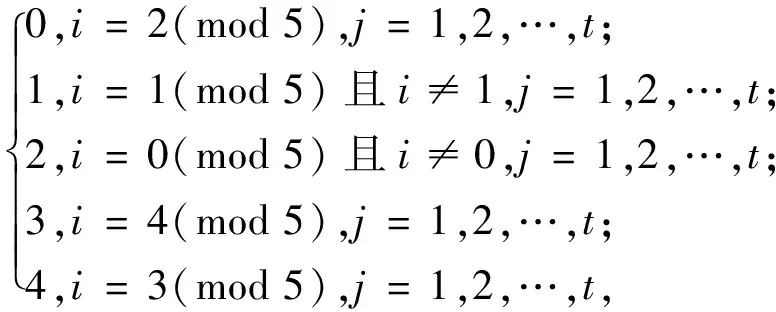
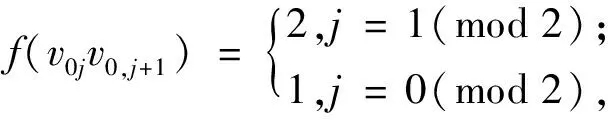
f(vijvi+1,j+1)=
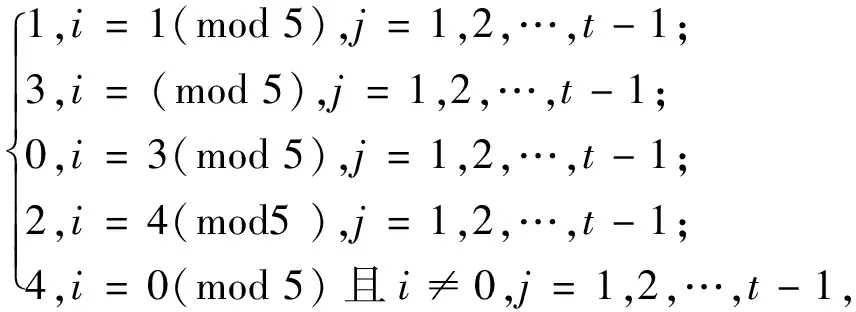
f(vijvi-1,j+1)=
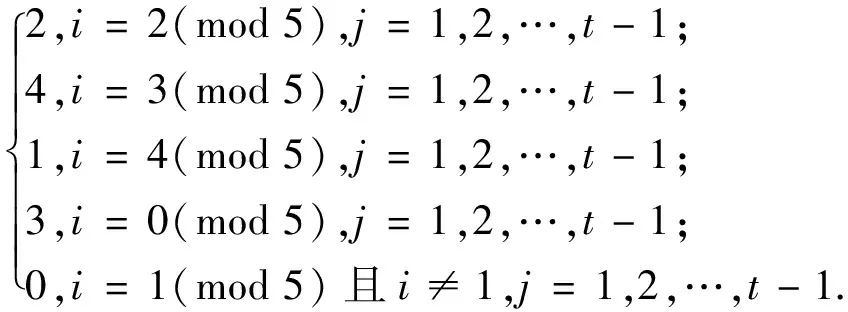
边v0jv1,j+1用3,3,4,4,0,0循环染色,边v1jv0,j+1用4,0,0,3,3,4循环染色.
为验证上述染色方法f是邻点可区别的,下面给出各顶点的色集合:
同情形1,顶点vi1(i=0,1,…,n),vnj(j=1,2,…,t),vit(i=0,1,…,n)的色集合无需再进一步验证.综上所述,此染色f为邻点可区别的,且各种颜色所染元素数均为
综上,由定义1可知f是图Mn(Pt)当n=1(mod 5)时的一个5-I-AVDETC.
情形3当n=2(mod 5)时,令f为顶点v01,v02,…,v0t依次用1,4,3,0,3循环染色;顶点v11,v12,…,v15用3,2,2,4,4染色;顶点v16,v17,…,v1t依次用2,2,2,4,4循环染色;顶点v21,v22,…,v2t依次用0,1,0,1,1,1循环染色;顶点v31,v32,…,v3t依次用4,4,4,2,2循环染色,且
f(vij)=
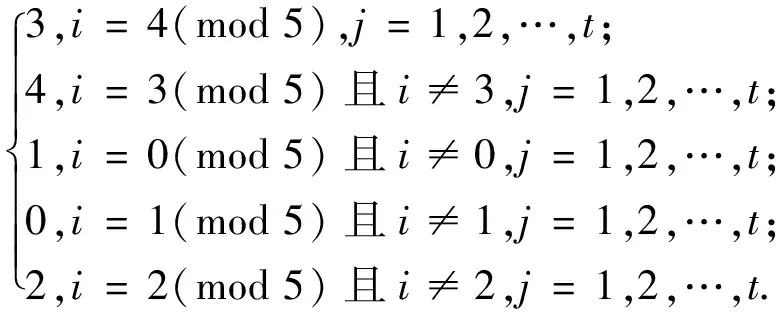
边v0jv0,j+1(j=1,2,…,t-1)依次用4,2,4,2,3循环染色.

f(v1jv0,j+1)=0,j=1,2,…,t-1;
f(v1jv2,j+1)=3,j=1,2,…,t;
f(v2jv1,j+1)=4,j=1,2,…,t-1;
f(vijvi+1,j+1)=
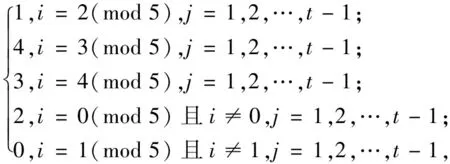
f(vijvi-1,j+1)=
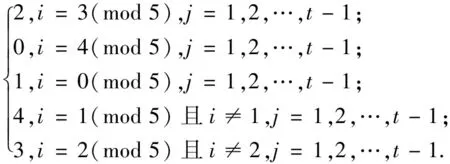
为验证上述染色方法f是邻点可区别的,下面给出各顶点的色集合:
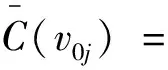

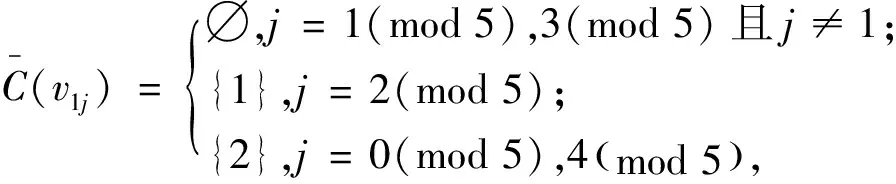
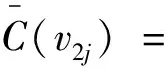
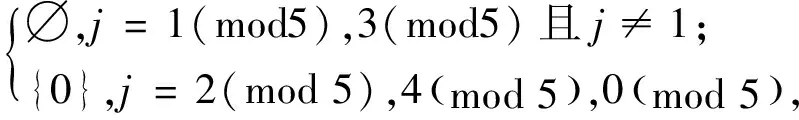
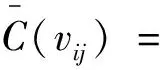
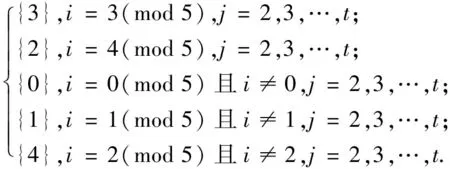
同情形1,顶点vi1(i=0,1,…,n),vnj(j=1,2,…,t),vit(i=0,1,…,n)的色集合无需再进一步验证.综上所述,此染色f为邻点可区别的,且有:
当t=0(mod 5)时,有
当t=1(mod 5)时,有
当t=2(mod 5)时,有
当t=3(mod 5)时,有
当t=4(mod 5)时,有
综上,由定义1可知,f是图Mn(Pt)当n=2(mod 5)时的一个5-I-AVDETC.
情形4当n=3(mod 5)时,令f为顶点v01,v02用0,4染色,顶点v03,v04,…,v0t依次用1,0,4,1,0循环染色;顶点v11用1染色;顶点v12,v13,…,v1t均用2染色;顶点v21,v22用3,0染色;顶点v23,v24,…,v2t依次用3,1,1,0,0循环染色;顶点v31,v32用1,2染色;顶点v33,v34,…,v3t依次用4,2,4,4,1循环染色,且
f(vij)=
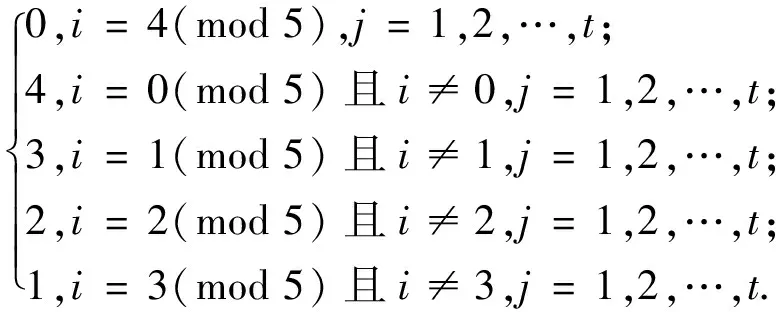
边v0jv0,j+1(j=1,2,…,t-1)依次用4,0,4,0,1循环染色.
f(vijvi+1,j+1)=
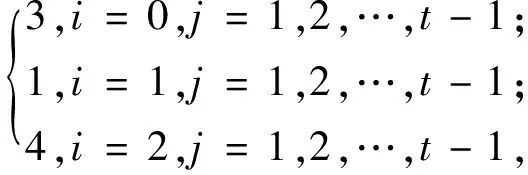
f(vijvi-1,j+1)=
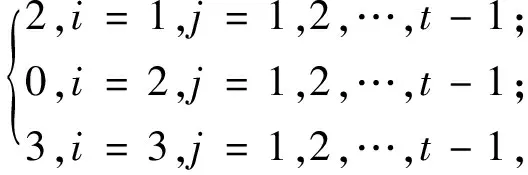
f(vijvi+1,j+1)=
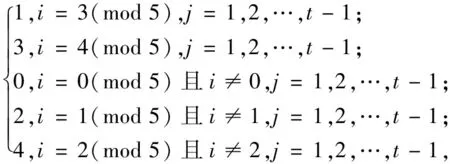
f(vijvi-1,j+1)=
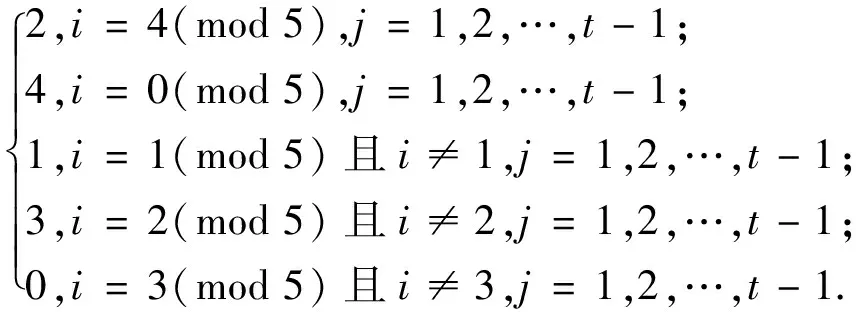
为验证上述染色方法f是邻点可区别的,下面给出各顶点的色集合:
同情形1,顶点vi1(i=0,1,…,n),vnj(j=1,2,…,t),vit(i=0,1,…,n)的色集合无需再进一步验证.综上所述,此染色f为邻点可区别的,且有:
当t=0(mod 5)时,有
当t=1(mod 5)时,有
当t=2(mod 5)时,有
当t=3(mod 5)时,有
当t=4(mod 5)时,有
综上,由定义1可知,f是图Mn(Pt)当n=3(mod 5)时的一个5-I-AVDETC.
情形5当n=4(mod 5)时,令f为顶点v01用0染色;顶点v02,v03,…,v0t依次用4,2,1,0,1循环染色;顶点v11用3染色;顶点v12,v13,…,v1t依次用3,3,4,2,3循环染色;顶点v21用2染色;顶点v22,v23,…,v2t依次用1,2,1,2,1循环染色;顶点v31用4染色;顶点v32,v33,…,v3t依次用0,0,0,4,4循环染色;顶点v41用1染色;顶点v42,v43,…,v4t依次用2,1,2,1,2循环染色;顶点v71,v72,…,v7t依次用3,2,3,3,3循环染色,且
f(vij)=



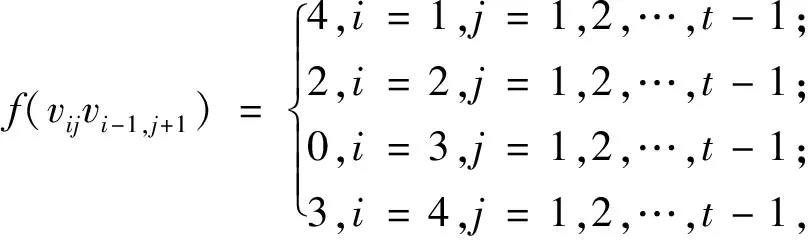
f(vijvi+1,j+1)=
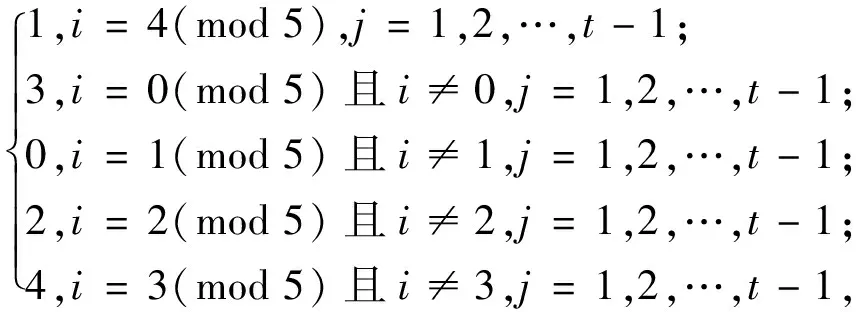
f(vijvi-1,j+1)=
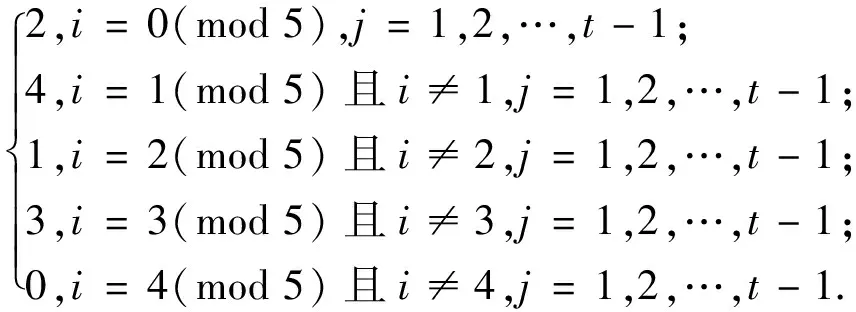
为验证上述染色方法f是邻点可区别的,下面给出各顶点的色集合:
同情形1,顶点vi1(i=0,1,…,n),vnj(j=1,2,…,t),vit(i=0,1,…,n)的色集合无需再进一步验证.综上所述,此染色f为邻点可区别的,且有:
当t=0(mod 5)时,有
当t=1(mod 5)时,有
当t=2(mod 5)时,有
当t=3(mod 5)时,有
当t=4(mod 5)时,有
综上,由定义1可知,f是图Mn(Pt)当n=4(mod 5)时的一个5-I-AVDETC.
推论1设Pt为t(t≥3)阶路,则
由引理1和引理2知此推论成立.
3 结语
本文研究了路的第一类广义Mycielski图Mn(Pt)的邻点可区别I-均匀全色方法和邻点可区别I-均匀全色数,所得结果验证了这类图满足邻点可区别I-均匀全染色猜想.在后续的工作中,将进一步研究第二类广义Mycielski图mn(Pt)的邻点可区别I-均匀全染色方法.
