外置分阶段耗能阻尼器自复位桥墩的抗震性能
2022-06-08李帆蒋玉玮黄海新
李帆 蒋玉玮 黄海新
河北工业大学土木与交通学院,天津 300401
随着“可恢复功能城市”理念的提出,人们对灾后结构的使用性和可修复性有了更高的需求,新型的自复位结构逐渐成为研究热点。不同于利用自身塑性破坏耗能的整体延性桥墩,自复位桥墩具有可恢复性好、残余位移低、地震损伤小的优点,比现阶段的“三水准”设防有更高的抗震性能,可做到“大震可修、大震易修”。1960 年的智利大地震中一个底部没有固结的水塔在地震中保存了下来,这是自复位结构的雏形,之后 Housner[1]提出了摇摆结构的理论。Mander等[2]将自复位结构的理念引入到桥墩设计中,通过在结构中加设无黏结预应力筋使其获得自复位能力,试验结果显示桥墩模型残余位移小,自复位效果明显,但耗能能力较差。Palermo 等[3]在桥墩断开处用钢筋连接使其屈服耗能,大大提高了自复位结构的耗能能力。李佰冉[4]为研究耗能钢筋对桥墩抗震性能的影响,建立了不同性能参数的自复位桥墩模型,发现耗能钢筋配筋率越高,桥墩的耗能和抗侧能力越高。虽然使用耗能钢筋使自复位桥墩的耗能能力大大提高,但钢筋安置于桥墩内部,屈服破坏后更换较困难。为实现可恢复、可更换的目的,学者们又尝试更换方便的外置耗能装置代替耗能钢筋。Marriott 等[5]制作了一种外置可更换耗能器,试验发现桥墩破坏集中于耗能器上,外置耗能器能起到良好的保护作用且更换方便。高慧兴[6]设计了一种可安装于桥墩外部的黏弹性阻尼器,通过试验和数值模拟得出阻尼器的附加阻尼和刚度能在一定程度上提高桥墩的耗能能力和水平承载力,且易更换。贾俊峰等[7]考虑到内置耗能钢筋不易更换的问题,对预制拼装自复位桥墩采用外置耗能器进行试验,发现外置耗能器耗能能力强,更换方便。
现阶段自复位桥墩设计时通常采用耗能钢筋或外置阻尼器以提高桥墩的耗能能力。耗能钢筋形式简单,但可修复性较差;阻尼器虽更换方便,但大部分桥梁阻尼器只具备一种耗能方式且只能单阶段耗能,很难满足结构在复杂多变地震环境下的抗震要求。针对上述问题提出一种外置分阶段耗能阻尼器(External Staged Energy Dissipation Damper,ESED),在不同强度地震下,ESED 耗能部件可逐级耗能,且外置结构更容易更换。本文基于实际工程缩尺试验,采用ABAQUS 软件建立阻尼器和自复位桥墩实体模型,通过拟静力加载的方式对比外置分阶段耗能阻尼器自复位桥墩(Self Resetting Pier with External Staged Energy Dissipation Damper,SRP‐ESED)与内置耗能钢筋自复位桥墩(Self Resetting Pier with Internal Energy Dissipation Reinforcement,SRP‐IEDR)的抗震性能。
1 ESED的构造
ESED 主体形状为直角扇形,便于安置在墩底与承台连接处,适用于矩形、圆柱形等多种桥墩类型(图1)。阻尼器的连接钢板开有螺栓孔,可在墩柱、承台内预埋钢板和螺栓以方便固定ESED。在地震作用下,桥墩发生沿墩底边缘旋转的左右摇摆,进而带动阻尼器转动工作。

图1 ESED安装示意
ESED 构造尺寸见图2。橡胶层制成与中间转动钢板相匹配的扇环型,厚10 mm,宽80 mm,放置于结构中间位置并通过硫化处理与两侧钢板固定。金属耗能部件为厚度不同软钢片,可根据承载力与耗能需求选择合适的数量,并对称焊接于中间转动钢板和两侧固定钢之间,以转动中心为圆心成扇形布置。桥墩发生晃动时,使其位于同等半径距离的耗能板各点具有相同转动位移,保证同厚度耗能板同时屈服、不同厚度耗能板分阶段屈服。
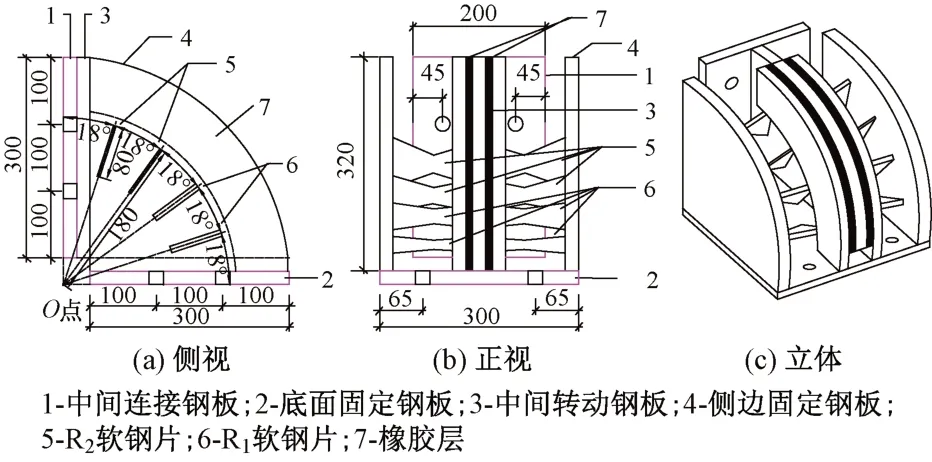
图2 ESED构造尺寸(单位:mm)
2 ESED的力学性能
2.1 ESED的功能
传统阻尼器一般分为位移型和速度型[8],前者利用材料的塑性屈服形变耗能,多为金属型耗能器,一般选择屈服强度低、塑性性能强的低碳钢;后者主要依靠内部的黏弹性材料发生剪切耗能,具有很好的可塑变形性和恢复性[9]。传统阻尼器虽然形式多样,但耗能形式单一。位移型阻尼器结构简单,耗能性能优异,但需达到金属屈服形变位移值后才能进行工作;黏弹性阻尼器虽更加灵敏,但材料刚度小,耗能能力有限,在大中型地震中对结构保护作用较差。
ESED 是将黏弹性阻尼器与金属阻尼器相结合,符合“综合利用不同耗能机制协同工作共同耗能”的思想[10],其耗能元件为高阻尼橡胶和厚度不同的软钢片。在正常工作荷载作用下桥墩微小晃动,只有橡胶变形耗能,软钢板仍保持弹性,此为第一道防线;在常遇地震等稍大荷载作用下桥墩摇摆幅度增大,大厚度软钢片屈服耗能,此为第二道防线;在中型或大型等罕遇地震作用下,桥墩摇摆幅度超过小厚度软钢片的屈服位移,使其协助橡胶层与大厚度软钢片共同耗能,此为第三道防线。各组件分阶段协同作用,充分发挥阻尼器的耗能性能。
2.2 ESED分阶段耗能机理
阻尼器的金属耗能部件为X 形弯曲屈服型耗能软钢片[11],见图3。该类型钢片塑性性能好,钢材利用率高。其中,h为软钢片高度;b为宽度;t为厚度;c为钢片中心最小宽度。
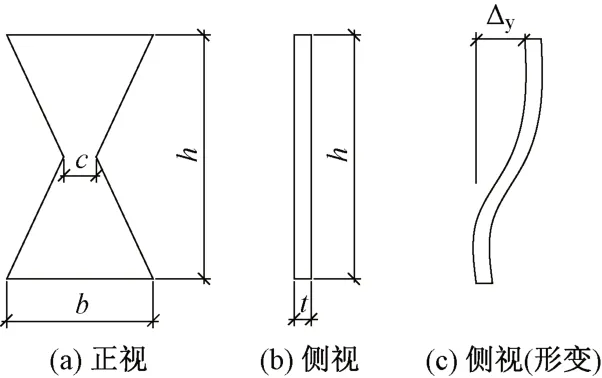
图3 X形弯曲屈服型软钢片
若不计中间最小宽度的影响,耗能软钢片的屈服剪力Vy、屈服位移Δy、初始刚度Ky分别为

式中:fy为屈服强度;E为弹性模量。
由上式可知,X 形弯曲屈服型软钢片的性能受屈服强度、高度、厚度等影响。因此,在阻尼器中设置了两种厚度不同而其他参数完全相同的软钢片(R1和R2),见表1。两种软钢片在共同加载形变过程中分别在不同的加载位移下屈服,依次参与耗能,从而实现阻尼器的分阶段耗能功能。
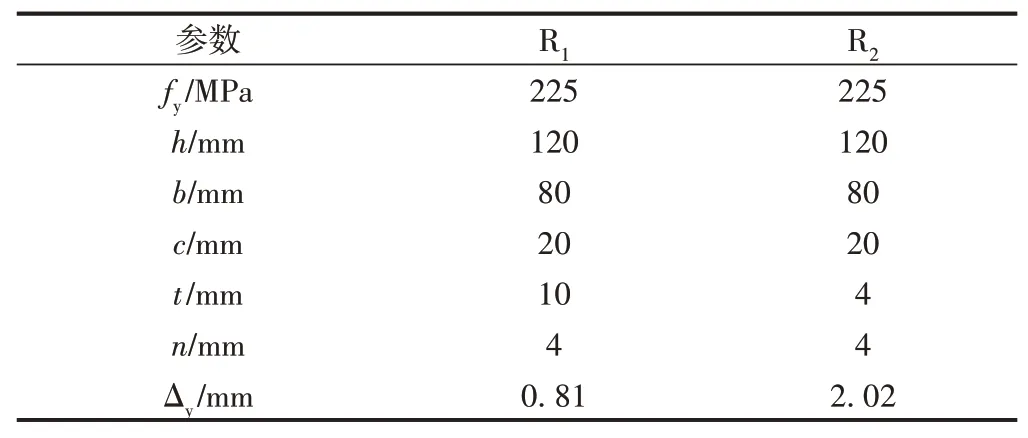
表1 软钢片设计参数
2.3 阻尼器软钢片配置原则
ESED 的软钢片可根据不同桥墩的承载力和耗能需求进行合理配置。自复位桥墩设计[12]中一般根据承载力进行耗能钢筋的设计。耗能钢筋截面面积公式为

式中:αED为耗能部件承载力替代系数;M为桥墩总承载力;bED为耗能钢筋距桥墩转动点距离;fyED为耗能钢筋屈服强度;k为自复位部件和耗能部件弯矩分担系数,建议在1.0 ~ 1.5[13]取值。
设计ESED 时可根据承载力等效原则将耗能钢筋承载力等效为阻尼器的承载力,包括橡胶变形恢复力和软钢片剪力。软钢片屈服剪力可由式(1)计算,橡胶变形恢复力FXJ计算式为

式中:KXJ、CXJ分别为橡胶等效刚度与等效阻尼分别为橡胶形变量和形变速率;A为橡胶与钢板的接触面积;d为橡胶的厚度;G′(ω)、G″(ω)分别为橡胶材料的储能模量与损耗模量。
3 ESED的数值模拟
3.1 阻尼器模型建立
利用ABAQUS 有限元软件建立阻尼器三维实体模型并进行数值分析。模型中阻尼器的尺寸均采用图2 数据,软钢片金属本构模型选用Von Mises 屈服准则与双线性随动强化模型,屈服强度225 MPa,弹性模量取200 GPa;橡胶为不可压缩或近似不可压缩材料,采用C3D8H 杂交单元模拟,并考虑超弹性与黏弹性。超弹性本构模型选用ABAQUS 中的Ogden 模型,参数采用文献[14]中拟合数值,具体参数见表2。黏弹性本构模型选用广义Maxwell 模型,在ABAQUS 中通过输入Prony 级数参数进行模拟,参数采用文献[15]中拟合值,具体参数见表3。

表2 橡胶超弹性参数

表3 橡胶黏弹性参数
3.2 约束及加载方式
模型中橡胶和软钢片均与周围钢板刚性连接,采用绑定约束。加载时将阻尼器底面固定钢板完全固接,在转动中心O点建立参考点并与阻尼器和墩柱连接的一侧钢板表面耦合,对参考点施加转角荷载即可模拟桥墩摇摆时阻尼器工作情况。
选择软钢片相对于转动中心200 mm 最外侧点屈服时的角度为阻尼器起始屈服转角,距其120 mm 最内侧点屈服时的角度为完全屈服转角。根据弧长公式和表1 中的理论屈服位移可得,R1的起始屈服转角和完全屈服转角分别为0.004、0.008 rad,R2的起始屈服转角和完全屈服转角分别为0.011、0.020 rad。为体现橡胶的黏滞性,采用频率1 Hz的正弦转角分两种工况加载(图4):工况一是最大转角为0.03 rad 的单方向一级加载;工况二是变幅值分级往复加载,每级循环两次,设R1、R2屈服位移对应的转角分别为Δθ1、Δθ2。工况二加载参数见表4。

图4 加载制度
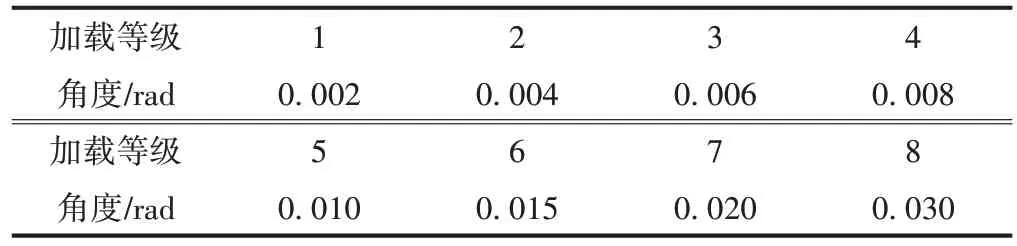
表4 工况二加载参数
3.3 阻尼器数值模拟结果分析
阻尼器在两种工况下的滞回曲线见图5。可知:分阶段耗能阻尼器的滞回曲线分为三段,表明阻尼器刚度在加载过程中因不同耗能元件分阶段参与耗能而发生改变;阻尼器的滞回曲线饱满,耗能能力良好;验证了阻尼器滞回曲线由黏弹性材料和金属材料滞回曲线叠加而成的理论假设。

图5 阻尼器滞回曲线
阻尼器软钢片应力变化云图见图6。可知,加载至0.002 rad时,软钢板R1、R2均处于弹性阶段,仅由橡胶剪切耗能,对应第一道防线;当加载至0.004 rad 时R1开始屈服,至0.008 rad时完全屈服,R2仍保持弹性,对应第二道防线;当加载至0.010 rad 时R2开始屈服,至0.020 rad 时完全屈服,对应第三道防线。这表明ESED达到分阶段耗能的预期效果。
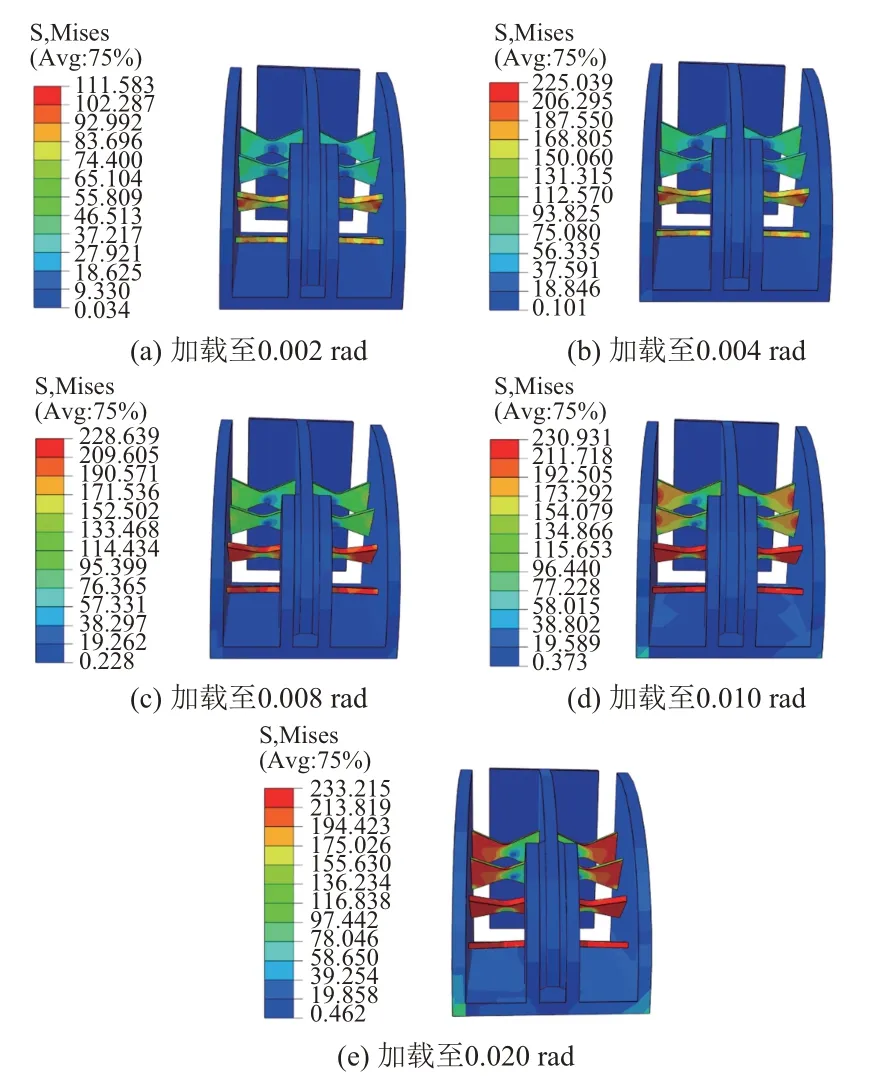
图6 阻尼器应力变化云图(单位:MPa)
4 自复位桥墩数值模拟
4.1 桥墩模型可行性验证
为研究SRP‐ESED 桥墩的抗震效果,以文献[12]中工程缩尺试验为基础,对 SRP‐IEDR 与 SRP‐ESED 进行数值建模分析。模型中桥墩各部件尺寸、材料、配筋等均与文献[12]中数据保持一致。其中钢筋采用T3D2桁架单元与双线性组合强化本构模型,预应力筋采用降温法施加预应力,设膨胀系数为1.2 × 10-5,总预拉力为320 kN,单根预应筋预拉力为80 kN;混凝土材料本构模型选用混凝土塑性损伤模型。桥墩结构尺寸见图7,桥墩部件设计参数见表5。

图7 桥墩尺寸(单位:mm)

表5 桥墩部件设计参数
4.2 桥墩模型的约束加载方式
在桥墩模型上部建立参考点RP1 与墩柱上表面耦合,模型下部建立参考点RP2,使其与承台下表面耦合,以方便施加荷载。对RP2 施加固定约束,对RP1施加竖直向下的轴力(220 kN)模拟桥墩承受上部结构0.05的轴压比。水平方向施加位移荷载,加载制度与文献[12]一致,分级循环加载,第一级加载5 mm,最大等级加载60 mm,中间每一级加载均比上一级增加5 mm,每级循环三次。模型验证加载如图8所示。

图8 模型验证加载示意
将根据文献[12]建立的自复位桥墩模型所得滞回曲线与试验曲线进行对比,见图9。可知:模拟所得滞回曲线变化趋势和形状与试验基本相同,两者水平极限承载力有所差异,水平极限承载力试验值约160 kN,数值模拟值约146 kN。原因是有限元模拟中混凝土和钢筋本构模型较为简单,没有考虑箍筋对混凝土的强化作用,钢筋屈服弹性模量数值选择较小等,故极限承载力模拟值略小于试验值,但误差较小,说明自复位桥墩的数值模型与试验基本符合。
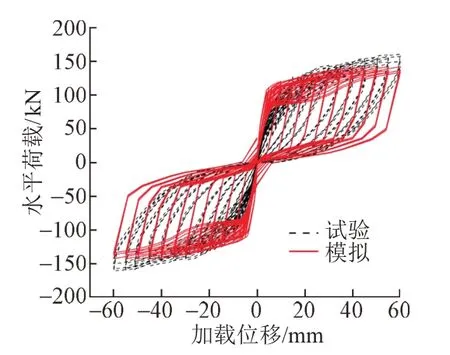
图9 滞回曲线
4.3 SRP-ESED性能和参数影响分析
建立4个自复位桥墩模型,分别为SRP‐IEDR模型SI 与 SRP‐ESED 模型 SE1、SE2、SE3(表 6),对比 SRP‐IEDR 与SRP‐ESED 的抗震性能和耗能钢板屈服强度对桥墩抗震性能的影响。按加载方向安置ESED 且设定加载方向为桥墩的最不利抗震方向,采用频率为1 Hz 的正弦加载。模型SE1—SE3 的阻尼器中两种软钢片数量均为4片。

表6 桥墩部件设计参数
4.3.1 滞回曲线对比
将模型 SI 滞回曲线分别与模型 SE1、SE2、SE3 滞回曲线进行对比,见图10。可知:①两种桥墩滞回曲线都明显呈旗帜形,残余位移小,自复位效果良好且捏缩效应明显;②SRP‐ESED 比 SRP‐IEDR 曲线形状更加饱满,且水平荷载承载力更高;③加载初期,SRP‐ESED 滞回环较小,说明软钢片还处于弹性阶段,仅由橡胶耗能,随着加载位移增大,软钢片逐级参与耗能,滞回环变大。说明SRP‐ESED 分阶段耗能状态良好,抗震性能优秀。

图10 四个桥墩模型滞回曲线对比
4.3.2 骨架曲线对比
骨架曲线是由滞回曲线中每次循环加载中的荷载极值点所绘制的包络图,可以直观展示结构在低周循环过程中水平荷载的峰值轨迹,反映结构在滞回过程中的刚度变化、承载力等。四个模型骨架曲线见图11。可知,模型SI、SE1、SE2、SE3 水平极限荷载分别为146、163、175、187 kN,模型SE3 比模型SI 提高约22%,说明SRP‐ESED 水平极限承载力较SRP‐IEDR 有较大提升,且随着软钢片屈服强度的提高而增大。

图11 四个桥墩模型骨架曲线对比
4.3.3 残余位移对比
桥墩摇摆过程中部分结构发生塑性变形使其不能在预应力钢筋作用下复原,从而产生残余位移。文献[16]中要求桥墩震后可修复的最小墩顶残余偏移率为1%(残余偏移率指桥墩停止受力后的墩顶残余位移与桥墩高度的比值百分数)。两种桥墩残余位移曲线见图12。可知:①加载前中期,两种桥墩的残余位移均较小且相差不大,表现出良好的自复位性能,加载后期,尤其加载位移达到50 mm 时,残余位移显著上升,原因可能是加载位移水平较大时,SRP‐ESED各部件均已屈服,塑性变形的累计导致残余变形增大。②模型 SE3、SE2、SE1、SI 最大残余位移依次为9.86、7.14、5.08、5.62 mm,其残余偏移率依次为0.58%、0.42%、0.29%、0.33%,可见屈服强度增大,桥墩的残余位移会略有增加,但仍满足小于1%残余偏移率的要求,可通过更换ESED 迅速恢复。SRP‐ESED自复位性能和震后可修复性良好。

图12 四个桥墩模型残余位移曲线对比
4.3.4 刚度退化对比
刚度退化指在循环往复荷载作用下保持相同峰值荷载时,峰值点的位移随循环次数增多而增大的现象。混凝土损伤开裂、钢筋和软钢片屈服等都会使桥墩刚度下降。根据规范[17]要求,采用割线刚度Ki来描述刚度退化曲线,计算式为
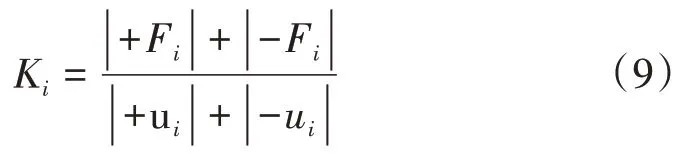
式中:+Fi、-Fi与+ui、-ui分别表示第i次循环加载极值点对应的正反方向荷载与位移。
根据式(9)计算四个桥墩模型的刚度退化曲线,见图13。可知:①4条曲线变化趋势基本相同,随着加载位移的增大,两种桥墩模型刚度退化较明显,且于加载后期逐级趋于平缓;②SRP‐ESED 刚度最终略大于SRP‐IEDR,原因是黏弹性耗能部件为桥墩增加了附加刚度且黏弹性材料刚度不会因为塑性变形退化,从而提高了桥墩的整体刚度,使桥墩具有更好的抗震性能;③结合式(3)可知,耗能板的初始刚度仅与几何尺寸有关,故SE1、SE2、SE3 的刚度退化曲线基本重合,耗能板的屈服强度对SRP‐ESED刚度影响较小。
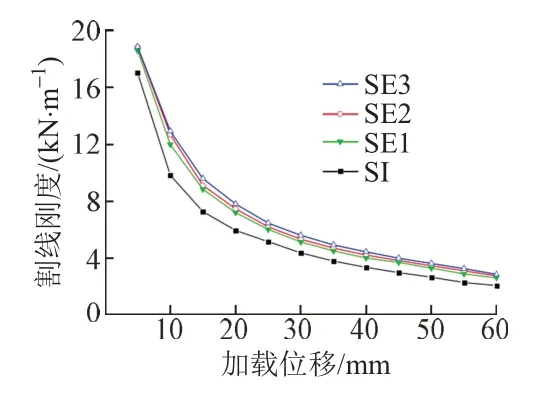
图13 四个桥墩模型刚度退化曲线对比
5 结论
1)SRP‐ESED 的滞回曲线饱满,三段曲线状的滞回关系满足理论假设,在不同等级荷载下能有效发挥分阶段耗能效果,提高阻尼器的耗能效率。
2)与SRP‐IEDR 相比,SRP‐ESED 滞回曲线更加饱满,水平极限承载力提高22%。可见ESED 中的两种耗能部件的复合式结构,提高了桥墩的抗震性能,增强了桥墩整体的刚度,减弱了桥墩刚度退化。
3)耗能软钢的材质对SRP‐ESED 整体抗震性能有一定影响。软钢片的屈服强度越大,桥墩的抗侧承载力越强,但对刚度影响较小;提高软钢片屈服强度虽会增加自复位桥墩的残余位移,但残余偏移率小于1%,满足抗震规范中可修复标准要求。
