上市公司债务信用风险评估——基于不同Merton模型有效性的研究

张紫薇

（南开大学金融学院，天津 300350）

一、引言

近年来债券市场违约主体的快速增长，对金融市场的稳定性带来较大挑战，但信用风险的及时暴露也可以更好地起到预防和化解更大市场风险的作用。在此背景下，债券违约风险正成为投资者、监管者以及学者高度重视的研究主题，有效识别和预测债券的信用风险，对预防大规模、系统性的违约风险和降低投资者的损失具有重要意义。

国际信用评级市场上，穆迪公司开发的KMV模型已经在许多发达国家用于信用风险评估（张玲等，2004），但对最适用于中国市场的信用风险模型还没有形成一致结论。目前，我国债券市场亟待发展出适用于中国市场的信用评级模型，让信用评级体系充分发挥信用风险预警的作用。本文正是在此目的上，对比研究不同的信用风险预测模型，考察 Merton模型风险评估的有效性，进一步提供其是否适用于我国上市公司的证据。

二、文献综述

Beaver（1966年）首次使用单个财务会计变量来预测企业破产，Altman（1968）提出了Z-score模型，并在之后的研究中不断拓展了该模型，使之可以运用在不同行业和不同国家（Altman，2018）， Ohlso（1980）、Zmijewski（1984）分别采用了Logit、Probit分析方法应用到企业财务困境预测中。但这类财务模型被一些学者认为缺乏理论基础，且财务报表反映的是公司过去的经营成果和财务状况，其容易被粉饰，运用会计数据存在一定的局限性。随后，学者们将期权定价理论运用到预测企业的失败上，发展出了结构化模型。一些学者通过研究证实Merton模型确实具有重要的预测能力，资产价值的波动性可能提供了关于违约概率的重要信息（Vassalou等，2004；Duffie等，2007）。国内学者对Merton模型对中国市场的适用性进行了大量实证研究，认为KMV模型可以有效辨别ST与非ST公司，对于中国股市是适用的（马若微，2006），但该类模型对违约风险的预测可能并未优于传统的统计模型（石晓军等，2005）。

国内外学者对两类模型的有效性和预测能力进行的对比研究没有得出完全一致的结论，违约距离和违约概率变量是否包含了会计信息不能反映的信息也有争议（蔡玉兰，2016）。Benos等（2007）对比了财务模型、拓展的Merton模型及联合财务会计变量和Merton模型的违约距离变量的混合模型，发现混合模型的信用评级预测结果最好。陈艺云（2016）、刘凡晖（2018）、张中秋（2019）等研究的实证结果表明，运用我国上市公司ST和非ST样本数据回归的混合模型的预测效果较好，具有一定的实用性。

基于国内外研究的已有成果，本文以主体信用评级反映上市公司的信用风险，运用Ordered Probit回归方法对比传统的财务模型、不同的Merton模型以及混合模型的解释能力和预测能力，检验Merton违约距离变量在我国资本市场的适用价值。本文的研究为Merton模型在我国的适用性提供进一步证据，为国内上市公司信用风险模型的选择提供一定的参考价值，丰富了信用风险领域的研究成果。

三、研究设计

1.样本选择

本文出于可以得到更多被评级机构覆盖的样本及最多违约样本的考虑，选择以2019年符合要求的上市公司作为研究样本。

本文主要研究的模型是Merton模型，估计违约距离等核心变量需要计算所有者权益、权益波动率、资产波动率等指标，而上市公司的这些数据相对容易取得，因此本文选择以上市公司为研究样本，具体筛选过程如下：①剔除掉金融类上市企业；②去除同时在B股、H股等其他股票市场发行股票的公司；③筛选出存在2019年中债隐含主体信用评级的上市公司。由于直接从Wind数据库中导出的数据一般不包括当年已经退市的企业，本文查找了2019年发生债券违约但目前已退市的样本11个。最终，经过筛选共得到226个样本企业，其中在2019年发生首次违约的公司14家。

本文226个样本的中债隐含主体信用评级有14个等级，包括AAA、AA+、AA、AA-、A+、A、A-、BBB+、BBB、BBB-、BB+、B+、C、D等级，从AAA级到D级，表示评级主体的违约风险越来越高。由于原始主体评级分类过多、过于分散，直接将原始评级用来拟合模型可能会影响最终效果，于是本文将14个评级分类重新划分为AAA（12个）、AA（75个）、A（103个）、BBB-B（22个）、D（14个）五大类评级，并分别赋值为1、2、3、4、5，本文用变量Rating代表样本的主体信用评级，原始及重新进行分类的样本评级分布情况如表1所示。

表1 样本评级分布

总体来看，这226个样本的原始主体评级分布呈现出类似尖峰厚尾的特征，反映了样本的整体信用评级较高、信用状况较好的特征，但是处于信用水平较高与触发违约之间的过度阶段的样本相对而言过少，这些特征与陈学彬等（2021）的研究样本所呈现的特征相似。

2.建立模型

（1）Merton Naïve模型

Bharath等（2008）的Merton Naïve模型是建立在Merton模型的基础上的，他们比较了不同计算方法下Merton DD模型的预测效力，提出了计算方式更简单的Merton Naïve模型，该模型简化了对市场价值和资产波动率的求解过程。研究结果表明该模型的预测能力至少与其他参数设定和求解算法的 Merton DD模型相同，他们基于研究结果提出模型的函数形式比求解方法更加关键的观点。由于篇幅限制，本文不对该模型进行赘述。

（2）拓展的Merton DD模型

Benos等（2007）对原始的Merton期权定价模型的假设进行了部分修改得到了拓展的Merton DD模型，新模型的假设如下。

①公司的资产价值At过程遵循几何布朗运动，漂移项为常数无风险利率r，扩散项为常数资产波动率σA。

②为了捕捉与杠杆相关的不确定性，假定违约点DPt跟随几何布朗运动，漂移项为常数无风险利率r，扩散项为常数λ（违约点的波动率），资产价值随机性的来源与违约点随机性的来源是相互独立的，后者是可以分散的，以此确保存在唯一的风险中性概率和真实的概率测度等价。

③资本结构分为短期债务、其他短期债务（债务期限在一年及以内）、长期债务、其他长期债务以及普通股权益，同时模型假设债务的回收率为随机变量，还考虑了股利的影响，但本文结合中国实际情况并未考虑股利因素。总资本A0的构成公式为：

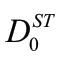
D的市场价值则从或有权益分析框架中债务的市场价值公式得到：

其中，RT为不同期限债务的回收率，RNEDPT为不同期限债务的风险中性预期违约概率。

在遵循了无风险利率为常数的假设以及违约、无风险利率和回收率互相独立的假设下可以推算出上式债务的市场价值，模型假定公司债务结构中存在期限为1年、2年、3年、4年和5年的债务，不同的债务期限取对应的T值代入上式中。但本文中考虑到中国市场有限的债务数据，中长期债务的期限假设为3年，短期债务的期限仍假设为1年。

下面总资产的市场价值A0可以进一步拆解成为下式：

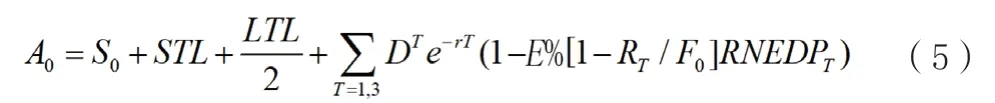
④在正态分布的假设下，风险中性预期违约概率RNEDPT和风险中性违约距离RNDDT可以写作：

⑤隐含的资产波动率Aσ可以从伊藤引理推导，得到下式：

资产价值 0A、资产波动率Aσ和违约点波动率λ不能被直接观测到，需要通过联立式（5）、式（6）与式（8）三个非线性方程组来求解。

（3）基于Merton模型的混合模型

传统的基于Merton期权定价模型的结构模型一般不考虑如流动性、营利性等财务方面的因素，也有学者认为结构模型估计出来的违约概率并不能反映出所有的信用风险因素，财务变量和市场变量都携带了一定的违约风险信息。为了检验财务比是否仍然可以提供有关公司信用风险的增量信息，Benos等（2007）不仅对单个违约距离变量进行检验，还将财务会计指标加入Merton模型中进行实证。他们估计了一个度量信用风险的混合模型，以风险中性违约距离指标、财务比率和其他基于会计的指标作为预测变量，用Ordered Probit回归模型进行预测，发现模型的解释能力和预测能力均有明显提高。

基于上述研究成果，利用已有财务数据和通过Merton模型得到的违约变量，本文尝试检验混合模型是否也适用于中国市场，混合模型的有效性和预测能力是否能够有所提升，是否可以更好地反映公司的信用风险。

3.参数计算

上述Merton Naïve模型、拓展的Merton DD模型及基于Merton模型的混合模型中的参数说明如下。

（1）权益波动率（Eσ）

对于Eσ的计算，采用了 Campbell等（2008）的计算公式：

其中ir代表每只股票第i天的收益率，样本股票的收益率数据来自CSMAR数据库，为考虑红利再投资的日个股回报率，N为样本股票全年的交易天数。

（2）违约点D0P

不少学者都专门对取不同违约点的影响进行过研究，部分研究得出的结论是不同违约点对违约概率的预测并无显著影响（Jessen等，2015）。本文违约点的计算方法采用的是拓展的Merton DD模型的计算方法，违约点D0P=短期债务+α×（长期债务-少数股东权益-递延所得税），所有数据都来自Wind数据库。本文也对比了取不同违点时的模型回归结果及预测结果来进行检验，让违约点计算公式中的α分别取0、0.5、0.75和1，得到不同α下违约点数据，用四个不同的违约点数据进行实证模型回归，回归结果和预测结果并无显著差别。本文按照以往惯例，违约点的计算中α仍然取0.5。

（3）无风险利率r

采用每年末中国人民银行公布的一年期定期存款利率，r取1.5%。

（4）权益的市场价值S0

权益的市场价值S0=期末收盘价×流通股股数，数据来自Wind数据库。

（5）Merton Naïve模型中的预期资产收益率μ

Agarwal等（2008）经过研究发现违约概率的估计对预期资产收益率取值并不敏感，因此本文按照一般做法，同样以无风险收益率替代，取每年末中国人民银行公布的一年期定期存款利率，μ=1.5%。

（6）债务到期时间T

本文采用年度数据，T等于1年和3年，Benos（2007）假设样本公司发行了债务期限分别为1年、2年、3年、4年和5年的债券，而我国上市企业的财务报表仅披露短期债务和长期债务，不对所有债务的期限进行详细说明，因此本文对该假设做了简化，假定短期债务的到期期限为1年，长期债务的债务期限为3年。

（7）债务的违约回收率RT与违约点的波动率λ

目前的研究对中国债券市场债务的违约回收率的估算较少，联合资信评估有限公司（2018）出版的报告估计目前公募债券市场整体回收率为24.17%。本文收集了2014年～2019年信用债中违约债券的偿还数据，估计了长期债券和短期债券各年的违约回收率及回收率的标准差，短期债券的违约回收率大约为35%，长期债券的违约回收率大约为 26%，长期债券违约回收率的标准差是22.74%，短期债券违约回收率的标准差为32.34%。遵循以往研究，本文把长期债券违约回收率的标准差作为违约点的波动率λ的代理变量，λ=22.74%。

（8）财务比率和会计数据

本文中财务模型仅作为基准模型提供参考标准，仅从般常用于财务困境预测的21个财务指标中选取了较为核心的三个变量：内部增长率、资产规模、息税前利润率，数据来自Wind数据库。

四、实证结果与分析

1.主要变量的描述性统计

本文实证模型中的主要变量的描述性统计结果显示：样本的主体评级（Rating）平均值为2.783，处于第二类评级AA至第三类评级A之间，这与样本评级分布结果相符，两类评级合计占比达到78.76%。从表2中数据来看，两种Merton模型计算出来的核心变量违约距离和违约概率的结果也相差较大。Merton Naïve模型得到的违约距离DD_Naïve的平均值达到1.118，远高于Merton DD模型计算出来的违约距离DD1和DD2，分别为0.500与0.276，Merton Naïve模型可能更倾向于高估了样本平均违约距离，从而低估违约风险，Merton DD模型计算的违约距离平均值较小，违约风险相对而言更高。两个模型计算出来的对应的违约概率也呈现出和违约距离相同的结果，Merton Naïve模型的违约概率平均值比Merton DD模型更低。选取的三个财务数据内部增长率、息税前利润率、资产规模的平均值也显示，样本的财务状况较好、资产规模较大。

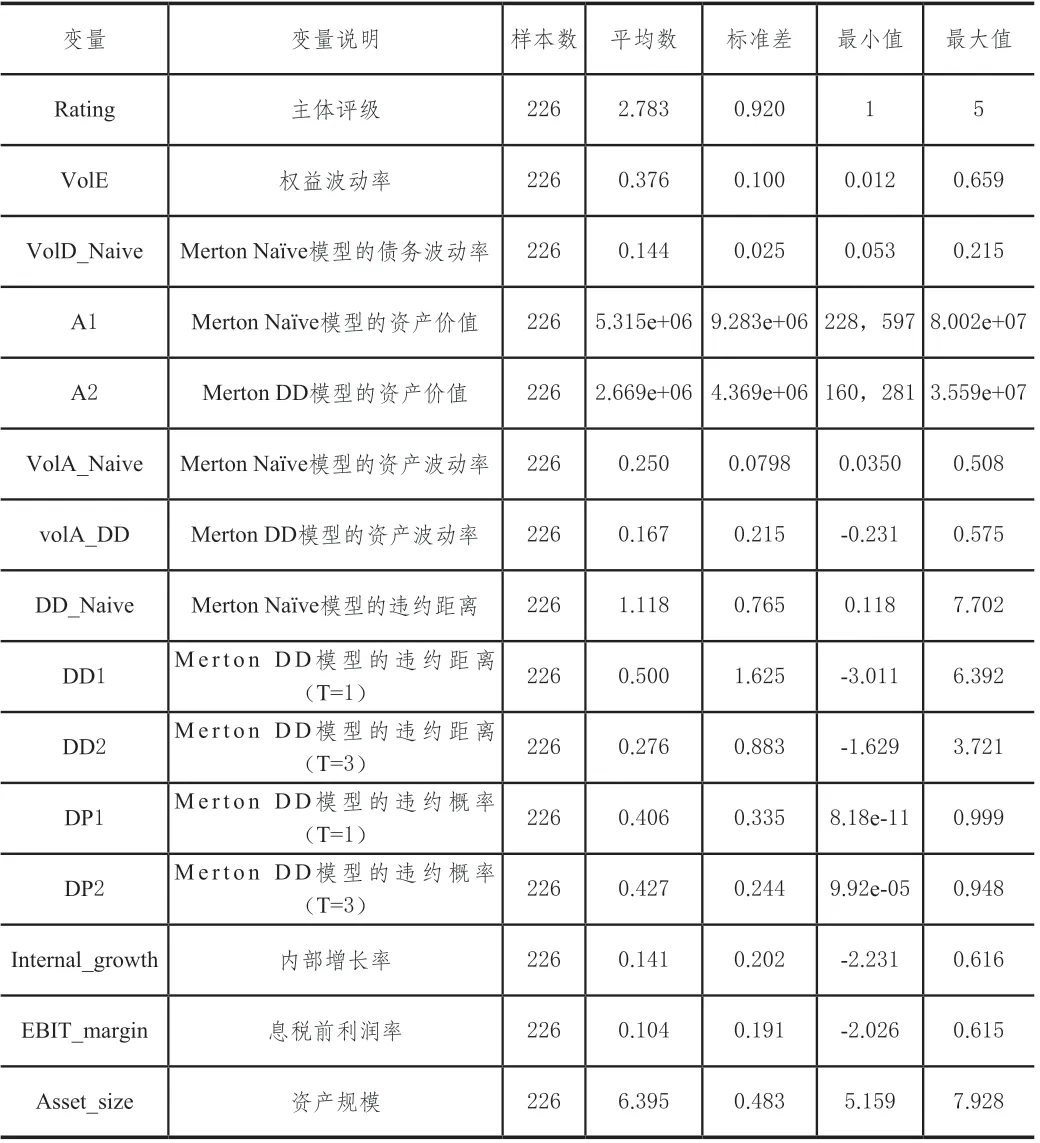
表2 模型变量的描述性统计

然而，在对模型进行多重共线性检验时发现DD1和DD2存在严重的多重共线性。如果两个变量存在多重共线性问题，则导致估计量非有效、参数估计值经济含义不明显、预测功能失效等问题。

为了解决DD1和DD2之间存在的多重共线性问题，保证模型估计结果系数的准确性，本文尝试了分别剔除DD1和DD2后进行回归。第一，与模型同时包含DD1和DD2的结果相比，分别剔除一个违约距离变量的模型不再存在多重共线性问题。第二，就回归参数而言，剔除DD2后， DD1也不再显著，而剔除DD1的模型中，变量DD2与主体评级相关性仍然显著，且回归系数也符合理论预期。第三，就预测效力而言，剔除DD1的回归模型预测效力与DD1、DD2同时存在的模型比较一致，无明显预测差异。

综上分析，本文在对比了主体评级与两个违约距离变量的相关性、回归结果系数的显著性及系数符号准确性、预测准确度后，选择剔除违约距离变量DD1，根据不同模型回归结果及预测结果来看，剔除DD1不会导致Merton DD模型的回归结果及预测结果产生较大差异，尤其是从预测结果来看，影响较小。本文仅呈现最终剔除变量DD1之后的估计结果。

2.模型回归结果

表3展示的是财务模型、Merton Naïve模型、拓展的Merton DD模型及混合模型回归的结果。在第一列财务模型回归结果中，内部增长率、资产规模变量的系数均在1%的显著性水平下显著，息税前利润率变量的系数在5%的显著性水平下显著，与相关系数矩阵展示的结果相同。内部增长率和息税前利润率反映公司的盈利能力，资产规模变量反映公司的大小，该财务模型更加关注的是公司的规模和盈利水平，规模越大、盈利水平越好，则公司的主体评级越高，违约风险越小。

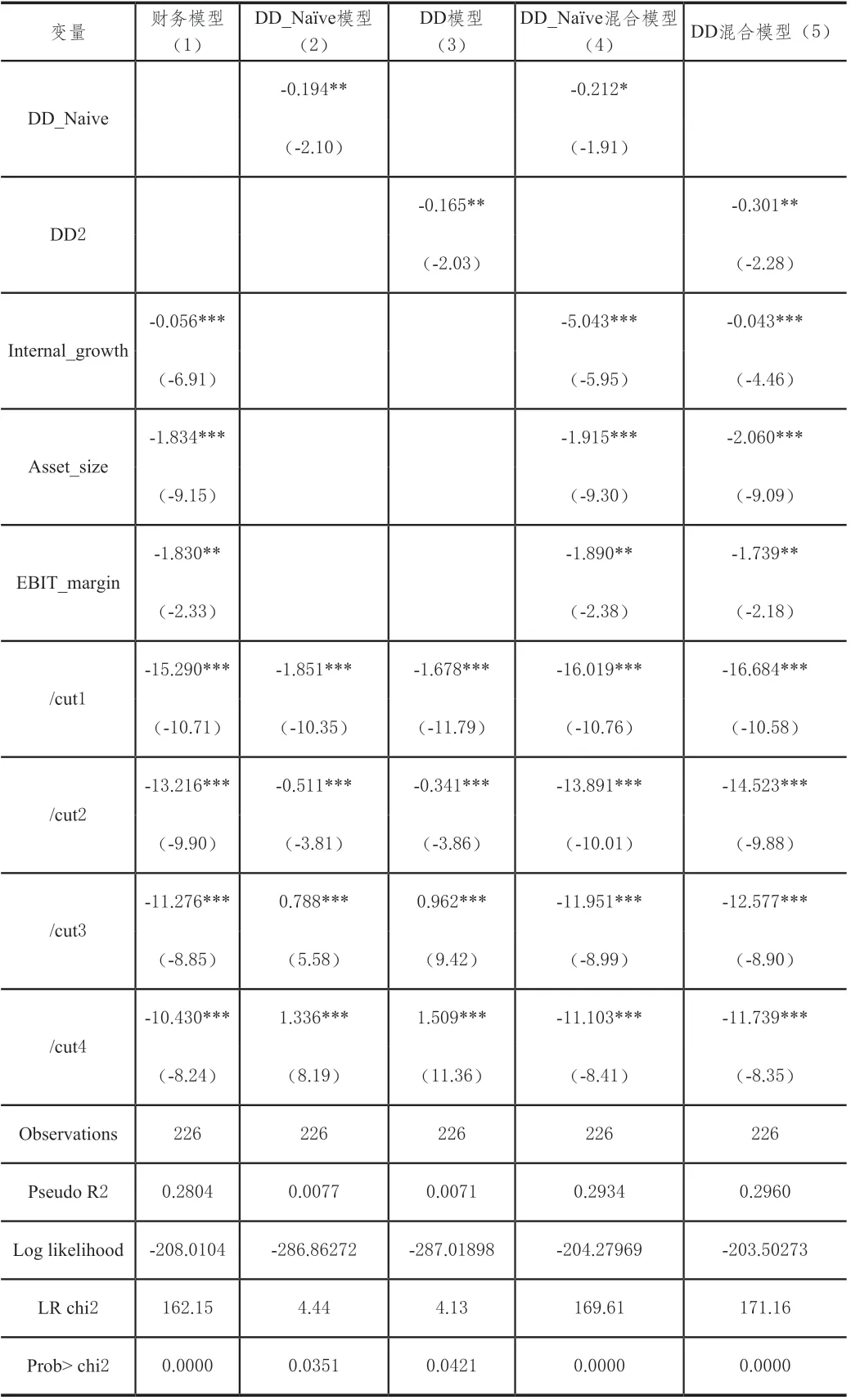
表3 模型回归结果

第2列与第3列结果是采用Ordered Probit回归方法对单独的违约距离变量进行回归的结果。违约距离表示的是公司的资产价值远离违约点的标准差。表中的回归结果显示，违约距离变量DD_Naïve和DD2均在5%的显著性水平下显著，两者系数符号均为负，结果和理论预期一致，违约距离越大，违约概率越小，从而主体评级越好，违约风险更低。但是Merton Naïve模型和拓展的Merton DD模型的解释能力都很小，远远低于财务模型的解释能力。违约距离模型的拟合结果不佳，表明其本身并不是评估企业信用质量的充分变量，这与同样运用国内债券数据进行研究的蔡玉兰（2016）的结论一致。

第4列与第5列分别是DD_Naïve混合模型与DD混合模型的回归结果。混合模型把违约距离变量与财务会计变量同时作为解释变量放入模型中进行回归。从表中的回归结果来看，DD_Naïve混合模型中的违约距离变量仍然是显著的，但是从原来的在5%水平上显著变为在10%显著性水平上显著，在加入财务会计变量后显著性有所降低。DD混合模型中的违约距离变量仍然在5%水平上显著，与违约距离作为唯一变量进行回归时相同，系数符号为负，没有发生变化。同样对比混合模型中的财务变量，可发现即使存在违约距离变量，但并未影响三个财务变量的显著性，内部增长率、资产规模变量的系数仍然在1%的显著性水平下显著，息税前利润率变量的系数也依然在5%的显著性水平下显著，系数符号、系数估计值大小均未发生较大变化。所不同的地方在于，两个混合模型的解释能力较纯财务模型有所增强，也远远高于单纯以违约距离变量为核心解释变量的Merton模型的解释能力。由此可见，违约距离变量的存在对Merton模型是有所改善的，但是改善的程度有限，并未做到大幅度提高模型的解释能力。

3.模型预测效果

表4展示的财务模型、DD_Naïve模型、DD模型以及混合模型的主体评级预测能力。从对各评级的预测能力来看，财务模型与DD_Naïve混合模型、DD混合对AAA评级、BBB-B评级和D类评级的预测能力相同，可以预测出1/3的AAA类样本主体评级和5/14的D类违约样本，但无法预测BBB-B类样本评级。对于AA评级，DD混合模型和财务模型预测能力相当，略微高于DD_Naïve混合模型；对于A类评级，DD混合模型预测结果最好，稍好于DD_Naïve混合模型于财务模型。而DD_Naïve模型和DD模型几乎无法成功预测AAA评级、BBB-B评级与D评级，这两类模型把大部分样本的评级识别成A类评级，缺乏预测能力。从样本的分布来看，评级最好的AAA类和较差的BBB-B类与违约样本D类的样本数量都占比很小，存在较严重的不平衡问题，但本文主要关注的问题在于不同形式的Merton模型是否有比传统的财务变量为解释变量更好的预测能力。综合比较，DD_Naïve混合模型和DD混合模型的预测能力并未显著高于财务模型，三者相当，也就是说，从模型预测能力来看，混合模型也并未显著较财务模型有提升。

综合表4的预测结果来看，我们可以得出的结论是，虽然运用不同方式计算出来的违约距离变量对主体评级具有一定的解释能力，在Merton模型和混合模型的回归结果中，系数均具有较好的显著性，系数符号也符合预期，但违约距离变量并没有比财务会计数据变量更好的预测能力和鉴别能力，即使将违约距离变量与财务会计数据变量结合起来进行预测，相对增强了模型的解释能力，但没有显著提高模型的预测能力。

表4 模型预测效果

五、结论

本文以我国2019年有存续和违约的信用债券且存在主体信用评级的上市公司作为样本，采用主体信用评级数据度量上市公司的信用质量，比较了传统的财务模型、拓展的Merton违约距离模型和Bharath等（2008）的Merton Naïve模型、以及综合了财务比率、会计数据和Merton违约距离变量的混合模型对信用评级的解释能力和预测效果，得到了以下结论：（1）本文选择了Merton 模型的两种拓展模型进行验证，结果发现采用简化计算方法的Merton Naïve模型与估计方法较为复杂的拓展的Merton DD模型，其估计出来违约距离变量在解释能力和预测表现方面无明显差异；（2）Merton违约距离变量在预测企业信用评级方面具有显著性，但是解释能力和预测表现却并不理想，违约距离变量所包含的信息量十分有限，无法预测违约事件；（3）结合财务信息和违约距离变量的混合模型的解释能力相对于财务模型有所提高，但其预测能力与财务模型一致，说明违约距离变量在信用风险预测时并未起到作用，财务会计变量对评价中国上市公司的信用评级发挥着不可替代的作用。综上，不同于主要发达国家资本市场的研究经验，本文的研究结果显示中国上市公司股票的违约距离变量所蕴含的信息较弱，远不及财务会计数据所包含的信用风险信息，Merton违约距离模型可能并不适用于中国的上市公司。

从数据层面来看，中国债券市场打破刚性兑付的时间并不太长，近些年的违约债券虽已经有较大增长，但从总量上来看，违约公司依然属于少数，导致样本的评级数据结构不平衡。至于样本的评级结构，相对而言中债资信评级机构已经是较为独立客观的评级机构，发行人付费模式下的信用评级结构更加失衡，单从本文的数据集来看信用评级仍然较为集中，我国的信用评级市场仍然需要进一步发展，独立信用评级机构应得到重视。

从Merton模型本身来看，根据DD的计算公式，资产波动率是较为核心的变量，变量所捕获的信息理应是财务信息所不能包含的股票市场信息，资本市场上股票价格充分反映公司信息是该模型严格依赖的条件，股票市场的有效程度对违约距离所能反映的信息量十分关键（谭久均，2005），而我国资本市场的发展程度与发达国家资本市场还有较大差距，违约距离变量对中国上市公司过于抽象（蔡玉兰，2016），这可能是Merton模型在我国股票市场不能很好发挥作用的一个原因。其次，Merton模型本身也是基于一些严格假设，所涉及的变量较多，每个变量都需要选用一定方法进行计算或估计，违约距离变量本身是通过间接估计出来的资产价值和资产波动率等计算出来的，计算过程中可能存在一些误差，不可避免地对估计结果和预测能力会产生影响，还有一些变量如债券回收率、违约点、债券期限结构等也是人为进行设定或计算，可能与真实情况存在较大出入，这些因素都会影响到模型的有效性和预测能力。

根据本文的研究结论，严重依赖股票市场有效性的Merton模型在我国适用性较低，财务会计数据所蕴含的信用风险信息对于预测我国上市公司违约事件是更为重要的考虑因素，因此发债主体所披露的财务信息质量尤为关键，近年违约上市主体不乏因财务数据造假导致投资者无法提前规避风险，监管机构应进一步严格要求发行主体信息披露质量。最后，国内现有主要评级机构应改善发布的评级真实性、客观性和独立性，及时根据公司情况发布跟踪评级，正确发挥风险预警作用，避免债券市场遭受突然的违约事件而产生剧烈震荡，监管机构也应鼓励更多的独立评级机构进入评级市场，完善信用评级体系。