基于U-Net的格子玻尔兹曼方法*

聂滋森，陈辛阳，杨耿超，蒋子超，姚清河

中山大学航空航天学院，广东 广州 510006

格子玻尔兹曼方法（LBM）［1］于20 世纪80 年代后期发展起来，为一种介观尺度下的流体模拟方法，与传统的通过求解纳维斯托克斯（N-S）方程来对流体进行模拟的数值方法相比较，LBM 物理概念更清晰，它易于并行，且擅于处理复杂边界，受到了很多科研工作者的关注，在流体力学，化学反应，量子力学，电磁学等各个领域广泛应用。然而，LBM 存在着对于计算资源的要求较高的缺点。具体来说，LBM 作为一个全显式算法，为了保证计算的稳定性以及精度，其计算的时间步长很短，而较短的时间步长导致计算迭代次数增多，使得对计算资源的消耗较高。本文从这一点出发，构造模型使得单次的模型计算代替多步的LBM迭代，以加快LBM的计算速度。

近些年来有很多尝试提升流体模拟计算效率的研究工作。有些研究提供了代替原来的求解泊松方程的方法，如Molemaker等［2］提出的迭代正交投影框架；Lentine 等［3］提出的粗网格投影法等。它们计算效率高，但它们的精度较低且仅对低分辨率问题有较好的效果。对于复杂的数值模拟问题，数据驱动模型是比较合适的优化方案，即通过给求解器供给足够的相关数据，使得求解器学习到该数据当中的统计信息。早期的数据驱动优化主要是基于模型降维（ROM，reduced order methods）的思想，如Treuille等［4］将N-S方程投影到低维的子空间上，以简化模型并提高计算效率，使求解器的计算速度能达到即时模拟的速度。早期ROM方法结构较为简单，而这也限制了其性能。

随着计算机硬件的发展以及机器学习相关理论和算法的成熟，越来越多的人将机器学习运用到流体数值模拟的加速当中。这类方法利用传统求解器计算得到的数据，训练得到一个机器学习模型，以代替原本耗时较长的计算步。如Ladick等［5］利用随机森林拟合拉格朗日描述下的N-S 方程，可以很大程度上简化原来的求解模型；另外他们还提出了一种针对平滑粒子法（SPH）的随机森林模型。上述机器学习方法较为传统，近年来发展起来的深层学习算法被证实能够更好地解决复杂问题［6］。其中，卷积神经网络（CNN，convolutional neural network）可以很好地对流体模拟这样的对空间信息十分依赖的问题进行优化。

研究者们还将原本复杂的迭代计算或求解过程转变为图像生成问题，如Yang 等［7］提出了基于CNN 的压力求解器模型，用以代替原本求解N-S方程过程中迭代求解压强的步骤；以此为基础，Tompson等［8］提出了一种非监督训练压力求解模型的方法，这种方法只需要较少的训练样本便可以得到求解模型。它们对于N-S 方程的求解有较好的提速效果且精度较高，但并不适合全显式的LBM算法。

在对于LBM 算法的加速中，Guo 等［9］训练CNN 模型直接由流场边界条件预测流场的稳定状态，这种方法加速效果明显，精度较高，但这对于非稳态问题以及需要关注流场发展过程的稳态问题并不适用。Hennigh［10］用一步的CNN 模型运算来代替LBM 的多步计算，这项研究关注于压缩内存的使用以实现更大幅度的加速，但模型存在一定的误差，在反复迭代中误差累积更为明显，生成的流场精度不高。

为适配非稳态问题并提高精度，本文构造了一个代替原来多个LBM 时间步的机器学习模型。在U-Net［11］基础上，引入残差神经网络（Res-Net，residual network）［12］以优化训练的效果，并在损失函数当中引入了流场的物理信息以进一步提升模型精度。

1 LBM数值模型

在LBM 数值模拟当中，流场被划分成很多等大的格子，利用每个格点上粒子分布函数f来描述该处流场的状态，在格点上用ft表示运动方向为ei的粒子数。本文所使用的针对二维问题的D2Q9 模型将粒子的运动方向离散为包括零向量的9 个方向，如图1所示。

图1 二维计算模型D2Q9示例Fig.1 Calculation model in 2D(D2Q9)

利用粒子分布函数可以得到该位置的其他物理信息，如宏观密度ρ和速度u为

其中r为格点位置，t为时间。LBM 离散形式的控制方程为

其中δt为时间步长，τC为松弛因子，Ω为由τC计算得到的碰撞因子。控制方程当中包含了对粒子迁移和碰撞两方面的描述，这两部分在数值程序当中分开计算，两者的表达式为

其中式（3）表述粒子的碰撞过程，式（4）表示粒子的迁移过程。

2 基于U-Net的LBM方法

2.1 网络结构

为了对LBM 进行加速，本文所采用的加速方案为压缩其计算迭代步，即通过给设计好的CNN提供大量的数据，训练出模型来代替原本多个时间步的计算。其时间步推进可归纳为

那么，可设计该加速方案的回归模型为

其中n为时间步长的跨越尺度，b为边界条件信息。

由这个回归模型，可以设计一个输入为t时刻的分布函数，输出为t+ Δt时刻分布函数的深层回归网络。对于本文所使用的D2Q9 模型，该网络的输入为10 个通道的一个“图像”，包括了9 个方向的粒子分布函数以及一个边界通道，输出为9个通道的“图像”，包括9 个方向的粒子分布函数。对于这类图像生成问题，往往采用的是编码-解码格式：先编码，即通过卷积（Conv）、池化（Pooling）进行深层次的特征提取；再解码，即通过反卷积（TransConv）或上采样（Upsampling）利用特征计算得到目标输出图像。但在实践当中，该问题极强的非线性使得这个模型的回归十分困难。为了提高模型精度，本文做了一些尝试，成功地将模型精度控制在较高的水平。本文构造的卷积神经网络结构如图2所示。

图2 基于U-Net对LBM加速的CNN网络结构Fig.2 CNN model to accelerate LBM based on U-Net

在实现这个编码-解码的结构时，卷积操作使用3 × 3 的卷积核，反卷积操作使用2 × 2 的卷积核，训练当中使用的优化算法为Adam［13］，卷积层激活函数的选取都为ReLu［14］，在训练过程中设置了学习率的衰减，使得模型在训练的后期收敛更稳定。网络结构参考了Olaf 等［11］提出的U-Net 网络结构。其关键在于在解码的过程中，将同等级的编码信息补充到解码信息当中去。该网络结构起初用于医学图像分割，起到了非常好的效果。之后，很多人将此网络结构用于其他的图像生成问题当中去，很大程度地提高了模型精度。随着神经网络层数的加深，一些关键的特征信息可能会丢失，而U-Net的连接层可以将这部分特征信息补充回来，很好地提升了图像回归问题的精度。

为显示U-Net对模型精度的提升作用，本文训练了另一组没有采用U-Net 的编码-解码结构以进行比较，发现精度的提升是巨大的：在训练300轮之后，U-Net 模型的平均百分比误差可以达到0.138 9%，而普通的编码-解码结构只能达到1.023 7%；且在实际的使用当中，普通的编码-解码结构生成的模型并不能维持住边界信息，且其生成的流场失真很严重。而仅仅应用了U-Net的网络结构也存在着一定的问题，单纯的深层网络很容易产生梯度弥散或梯度爆炸的问题。加了正则化层［15］的深层网络可能会解决这种问题，但它不能解决深层的网络经常会出现的模型退化问题。对此，本文参考了He 等［12］提出的ResNet 对卷积层进行了优化，见图2。

残差神经网络被运用在了图像识别问题上，很大程度上提高了模型的精度，其关键在于Shortcut 连接层。理论上，多层的神经网络可以拟合任意函数，但过于深层的网络很容易导致模型退化而使得模型无法收敛。通过Shortcut 连接层，可以在层数“多余”的时候将多余的层短接掉，以此避免模型的退化问题。在训练的过程中，本文将残差块应用到流场的编码与解码过程中，发现残差神经网络对于训练效果的提升是很大的，提高了模型精度以及收敛速度。

2.2 损失函数

损失函数是模型训练过程中用来评价模型优劣以帮助模型训练的工具。对于回归问题，往往使用的是L2的损失函数（MSE，mean squared error）

其中i表示通道数，对应D2Q9中9个方向，下标为“pred”的值为模型预测结果，下标为“true”的值为真值。

L2损失函数在回归问题当中效果是比较不错的，但它并不包含一些非常关键的物理信息。针对LBM，本文将一些关键的物理信息包含到了损失函数当中。针对不可压粘性流体密度不变的性质，可以写lossρ为

另外，针对不可压粘性流体流场速度散度为0的性质，可以写

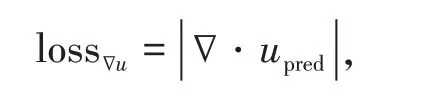
其中

所以，本文的损失函数为

其中μ1，μ2，μ3为系数。

对于相同的训练集，利用不同的损失函数进行训练。如图3所示，最终得到的两模型中包含了物理信息的LBM损失函数（μ1= 1，μ2=μ3= 0.05）精度略高于MSE 损失函数。由于该模型在进行数值模拟时需要进行反复地迭代，这种微小的精度提升对模型的稳定性会有一定的提升。

图3 模型训练过程中损失函数值Fig.3 Loss function of the model during training

3 算例实验

3.1 模型训练

本文设计用以证明模型有效性的算例为层流绕柱群的流场模拟。这种算例有比较复杂的漩涡结构，能够挑战模型学习复杂流场信息的能力，也能较为直观地看出模型的误差。算例的左侧为0.02 m/s的流入边界，右侧为流出边界，上下设置为了周期性边界，障碍物为无滑移碰撞边界。训练集为20 组层流流过三个并排的几何形状不同（圆、椭圆和正方形）、大小及位置随机的障碍物（如图4所示），这样的设置可以使模型对于障碍物的形状以及位置更敏感，提高模型的泛化能力。其余的参数设置如表1。

表1 训练集LBM仿真参数设置Table 1 Parameter setting for LBM simulation training set

图4 部分训练集Fig.4 Part of the training data set

设置的跳步数量为n= 200，即模型的回归模型为

对于本文所涉及的U-Net 模型，输入为t时刻的粒子分布函数和流场边界信息，输出为t+200Δt时刻的粒子分布函数。其中，对于本文后面所涉及的算例，流场中仅包含了碰撞边界，那么输入方式为二进制数组，在有障碍物的地方该数组的值为1，其他地方为0. 图5为一个二维的正方形障碍物边界例。

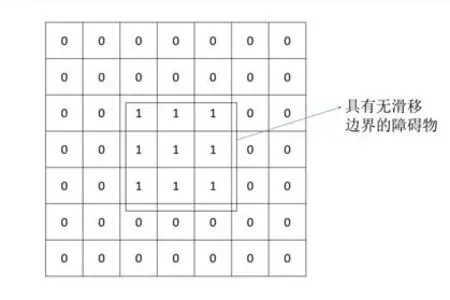
图5 几何边界输入Fig.5 Geometry boundary input

作为数据的预处理，将输入到训练当中的所有数据都进行了放大处理，因为流体系统是一个非常精细的系统，其临近点之间的差异可能并不是很大，如果直接将没有经过处理的数据输入到训练当中去，有很大的可能会造成模型最终收敛得到整个流场为一个平均值。

由于计算的前1 000 个时间步流场的变化往往比较小，可能会影响训练的效果，所以训练集采用的为第1 000 个时间步之后的计算结果，那么在使用模型的时候也是先利用LBM 计算1 000 步之后再调用训练好的模型。训练时所使用的批大小为50，训练300轮得到最终模型。

3.2 误差分析

首先，对本文所提出的损失函数lossLBM做误差分析。包含一定的物理信息势必会使得模型更贴近真实的物理状况，在实际的训练当中也可以看出精度的提升，如表2所示。

表2 训练至300轮时模型精度比较Table 2 Accuracy of the model after 300 epochs of training%

若系数适当，该损失函数的效果略微优于MSE，通过对系数的进一步优化，可达到更好的结果。而系数设置不合理可能会使得模型的训练更为困难，这是因为本文所引入的两个物理信息在数量级上略大于MSE，比较大的系数会使得模型更难以收敛。

下面在实际的算例当中调用模型，来看该模型的性质。对于训练集内部有的算例（算例1）来说，U-Net 模型的表现非常不错，计算结果如图6所示。直观来看，U-Net 模型的计算结果几乎与LBM 的计算结果完全一致。为更清晰地看出模型的误差发展，利用下式计算模型的误差，即其中i表示通道数，对应D2Q9中9个方向，j和k分别表示点x方向位置以及y方向位置，nx和ny分别表示x方向格点数及y方向格点数，nlattice为总格点数。

图6 算例1流场速度图（第一行为LBM计算结果，第二行为U-Net模型的计算结果）Fig.6 Velocity field of example 1(the first line is generated by LBM,the second line is generated by U-Net model)

由图7所示，随着对于模型的迭代，结果的误差增高，但其精度仍控制在较高水平。经过30 次的迭代后，计算得到的粒子分布函数的相对误差在1%以下，绝对误差在0.000 7 左右。在第30 个迭代步（对应的LBM 模型的计算步为第7 000 步），取流场中心一列做速度分布图，见图8。从图中可以看出，CNN 模型可以很好地学习到流场的流动规律，计算所得流场的速度水平分量和竖直分量都能较好地与LBM 数值模拟的结果相吻合，U-Net模型对于训练集当中所有的算例精度很高。

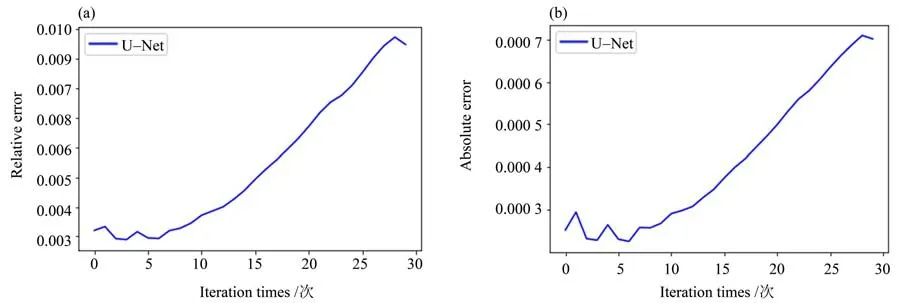
图7 算例1误差发展图Fig.7 Development of error of example 1

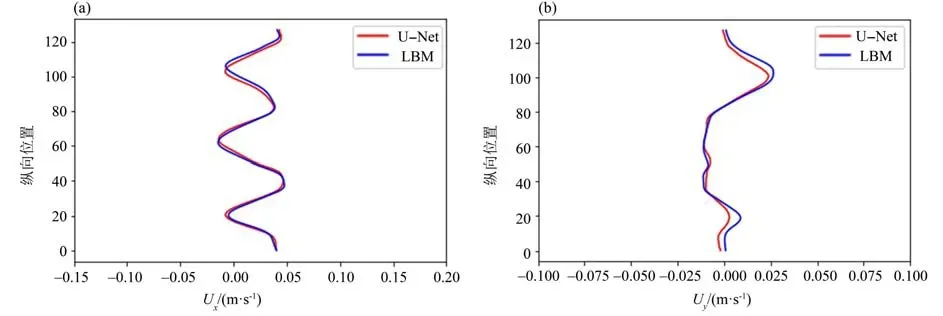
图8 算例1迭代30次后流场中心线上的速度分布Fig.8 Distribution of flow field centerline velocity of example 1 after 30 times of iteration

对于训练集以外，但是相似度与训练集当中算例较高的算例，以三个障碍物均为正方形为例（算例2）。该算例是训练集当中所没有的，计算结果见图9。对于该算例来说，虽然可以直观地看出U-Net模型生成流场的误差，但其生成的流场还是比较真实的。

图9 算例2流场速度图（第一行为LBM计算结果，第二行为U-Net模型的计算结果）Fig.9 Velocity field of example 2(the first line is generated by LBM,the second line is generated by U-Net model)

该算例的误差发展如图10 所示，对于更加泛化的算例，模型的计算结果误差相较于训练集中的算例（算例1）稍高一些，经过30次的迭代，其相对误差积累到了1.5%左右。在第30 个迭代步（LBM 的计算步为第7 000 步），取流场中心一列做速度分布图（见图11）。从图11可以看出，模型计算得到的水平速度分量精度较高，与LBM 计算结果吻合地较好；竖直的速度分量与LBM 计算结果之间有一定的误差，但二者趋势一致，且误差在数值上较小，对整体精度的影响有限。综合以上，该模型精度较高，且有一定的泛化能力。

图10 算例2误差发展图Fig.10 Development of error of example 2

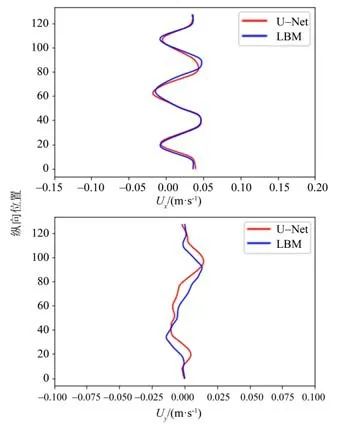
图11 算例2迭代30次后流场中心线上的速度分布Fig.11 Distribution of flow field centerline velocity of example 2 after 30 times of iteration

3.3 加速效果分析

本文所提出神经网络回归模型的目的为提升计算效率，将它利用在一些不需要很高精度且对计算速度有一定要求的算例当中。因此，我们需要对U-Net模型的计算速度进行一个评估。

对LBM 方法运算表现的评判标准为每秒百万格子更新数，其表达式为

其中nl为格子数，T为计算耗时。

本文的测试平台参数为：CPU：Intel（R）Xeon （R） W-3175X CPU @ 3.10GHz； GPU：RTX2080Ti 。实现算法的编程语言为Python 3.7，神经网络回归模型的训练和预测是通过深度学习开源库Keras 所实现的。LBM 的浮点数计算为双精度计算，而由于双精度计算的CNN 模型几乎不会有任何的精度提升，且会大幅降低计算速度，本文CNN模型采用的是单精度浮点数。

在调用模型时进行计时，测定神经网络模型的加速效果。以格子数为1282的二维算例为测试算例。调用模型，并将其与LBM计算200个时间步进行比较；与一些其他算例下利用GPU 并行计算对LBM 进行加速的计算效率进行比较，结果见表3。可知：（1）根据这个标准计算， U-Net 模型的计算速度相对于GPU 的并行计算还是要快一些。但需要注意到的是，表3中两个GPU并行的测试算例与本文所选取的算例不一致。在进一步的测试中发现，U-Net模型对于更大尺度上的算例有着更好的加速效果，测试结果如图12 所示。（2）该模型在更大尺度的流场上加速效果会更好，MLUPs 最高大致在1 600左右。

图12 计算效率与模型尺度的关系Fig.12 Relationship between calculation efficiency and scale of the model

表3 计算效率Table 3 Calculation efficiency

综上，该模型能显著加快LBM 的计算，尤其在大尺度的数值模拟当中，得到的加速效果比较好。

4 结 论

本文提出了一种基于U-Net 的对LBM 进行加速的卷积网络神经结构，引入残差神经网络预防了深层神经网络的退化，并设计了一个包含物理信息的损失函数，在一定程度上提高了模型的精度。为验证该模型的有效性，本文进行了数值实验。其结果表明，本文所提出的模型能够在保证精度较高的同时，实现很大程度的加速。另外，该模型是具有一定的泛化能力的。