低压配电网三相负荷不平衡优化模型的构建及应用

李 杰

（上海宝冶集团有限公司，上海 200000）

用电量的不断增加导致配单侧三相负荷不平衡问题十分突出，引发了配电网作业不良问题，主要体现在用电质量下降、部分电器设备损坏、线损增加、变压器损耗等多个方面。这不仅给用户带来了不便，也导致了配电网运营经济损失。低压配电网作为影响最大的网段，配电网运营期间随着三相负荷不均衡现象，导致线损问题的产生。如何解决三相负荷不均衡问题，是当前配电网作业优化的要点。当前针对该问题的探究，拟定的三相负荷不均衡问题优化方案，计算量较大，调节效果并不显著。该文尝试采用粒子群智能优化算法作为研究工具，尝试构建一套低压配电网三相负荷不平衡优化模型，并进行深入探究。

1 低压配电网三相负荷不平衡与用户负荷之间的量化关系分析

考虑到用电负荷存在一定动态特性和随机特性，通常情况下，三相负荷平衡状态很难长期存在，并且不存在绝对的平衡。即便如此，仍然存在一个方案，能够使不平衡度控制到最小。所以，关于该问题的探究，转变为单相负荷用户接入相序的设置优化处理。通过调解相序，来降低不平衡度，从而达到简化问题的目的。

在构建优化模型之前，需要明确用户负荷与不平衡度之间的关系。假设时间段内，分项（∈{B，C，D}）用电负荷为P，配电网作业功率因素为cos，平均相电压为U。在该基础上计算平均分相电流，如公式（1）所示。

式中：I代表平均分相电流。

假设B 项平均负荷电流为I，C 项平均负荷电流为I，D 项平均负荷电流为I，零线负荷电流均值为I。计算三相不均衡度，如公式（2）所示。

式中：代表三相不均衡度。

如果三相负荷中存在中性线，产生该现象的主要原因为线路中电流引发不均衡，对电压影响不大。为了简化问题，假设单相电压均值相等，功率因素相同，数值均为1，利用公式（1）～公式（3）计算三相不均衡度，如公式（4）所示。

式中：代表三相不平衡程度；、、代表B 相、C 相、D 相的用电负荷。

2 低压配电网三相负荷不平衡优化模型的构建

根据上文提及的低压配电网三相负荷不平衡与用户负荷之间的量化关系，构建不平衡优化模型。假设某低压台区用户数量为，可以用公式（5）的矩阵来描述用户负荷接入相序：

公式（5）中，为0-1 矩阵；x∈{0，1}，用于描述负荷是否接入Φ 相。的取值=1，2，…，。当=1 时，代表序号为的负荷接入Φ 相，当=0 时，认为序号为的负荷未接入Φ 相。

假设用户接入电网负荷统计结果中，每个用户的负荷相同，均为单项负荷，那么存在++=1 关系成立。假设用户表箱编号为=[，，…c]，用电负荷为=[，，…p]，换相成本为=[，，…d]。对编号为的用户电表是否换相的描述，用（，，）表示，取值范围（，，）∈{0，1}。如果该数值为1，则认为当前用户电表换相，如果该数值为0，则认为当前用户电表未换相。

在分析用户电表换相问题时，需要将表箱看作一个整体。假如多个用户电表所连接的表箱相同，则认为这些用户的电表换相之前和换相之后的相序保持不变。该关系为将用户与用户的电表连接到同一个表箱，存在[，，x]=[，，]关系成立。为了得到最小换相成本，尽可能降低三相负荷不平衡度，构建模型如公式（6）所示。

令[，，]=P，求解三相负荷不平衡度最小值，如公式（7）所示。

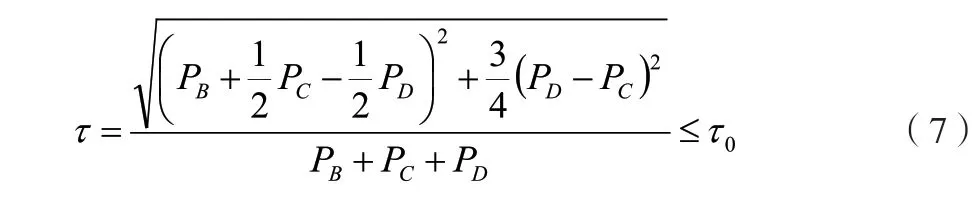
公式（7）中，代表三相负荷不平衡度的容许最大值。

3 低压配电网三相负荷不平衡优化模型的计算

3.1 粒子群算法核心流程

考虑到粒子群算法编程难度较低，具有较好的鲁棒性能，收敛速度较快，符合复杂模型数据计算需求。所以，该研究选取粒子群算法作为模型求解工具，模型计算核心流程。如图1 所示。

图1 粒子群算法核心流程

第一步：统计用户用电负荷相关数据，将该部分数据局存入excel 表格中，然后读取表格中的负荷数据。其中，数据读取方法为xlsread。模型维度的统计以用户数量统计结果为准。第二步：选取粒子群算法作为模型计算算法开发工具，根据模型中的参数关系，设置关于粒子群算法应用方案的参数。第三步：选取rand 方法作为数据处理工具，待速度和粒子群位置初始化结束后，开始迭代计算。其中，时间初始值为0。第四步：运用公式（5）计算各个粒子的适应度，结果记为fitness（），利用适应度计算结果，确定换相成本。第五步：根据前几个步骤的计算结果，确定当前全局极值和局部极值，并加以更新。第六步：根据最新参数数据，确定当前粒子位置和粒子速度数值，并更新这2 个数值。第七步：判断当前时间是否超过了设定的最大时间，如果超过，则执行第八步，反之，时间参数加1，返回第四步。第八步：结束该次模型计算，同时输出全局极值，确定最优相序。

3.2 模型计算程序设计

该研究选取MATLAB 软件作为模型计算程序开发工具，根据上文设计的粒子群算法核心流程，开发模型算程序。以下为本算法的核心程序：

通过运行上述程序，获取最优相序计算结果fitness（X（j，：））。通过分析fitness（X（j，：））相关数值特点，可知当前配电网区域内三相负荷调整需求，将其作为三相负荷调整根据优化相序，将不平衡度控制到最小。

4 案例分析

4.1 用户用电量统计

低压台区配电网接线较为复杂，涉及的线路除了单相两线制、三相三线制以外，还包括三相四线制接线。该研究选取单相两线制接线与三相四线制接线混合线路作为研究环境，统计该配电网环境下用户用电量相关数据，以月为单位统计，结果如表1 所示。

表1 用户用电量统计（kW·h/月）

根据负荷不平衡判断标准，如果最小值超过10%，认为当前线路中三相负荷不平衡问题较为严重。运用该文设计的低压配电网三相负荷不平衡优化模型计算相关数值，获取三相负荷不平衡度最小值。计算结果显示，=17.74%。该数值超过了10%，由此判断在该线路中三相负荷不平衡问题较为严重。

为了优化三相负荷不平衡问题，该案例研究，运行基于粒子群算法的最优相序计算程序，获取最优相序计算结果fitness（X（j，：））。通过分析该函数中数值分布特点，明确当前配电网区域内三相负荷调整方向，来调整三相负荷不平衡度。

4.2 负荷相序优化

该研究提出的负荷相序优化方案，建立在成本控制基础上。假设配电网区域内的所有用户换相成本相同，均为1。运行基于粒子群算法的最优相序计算程序，得到最优相序。按照最优相序，对案例中配电网相序进行调整，主要方案如下。1）编号4 的表箱用户中相序调整：C 相→B 相；2）编号5 的表箱用户中相序调整：B 相→C 相；3）编号8 的表箱用户中相序调整：D 相→C 相；4）编号9 的表箱用户中相序调整：D 相→B 相；5）编号13 的表箱用户中相序调整为B 相→D 相；6）编号14 的表箱用户中相序调整为C 相→B 相；7）编号15 的表箱用户中相序调整为B 相→A 相。

为了验证该文提出的基于粒子群算法的最优相序计算程序的可靠性，对优化后的相序方案进行检验。按照最新的相序方案调整配电网作业参数，统计用户用电量，将此部分数值重新带入三相负荷不平衡优化模型进行计算。结果中=2.35%，该数值低于10%。因此可以判断该文在不平衡优化模型基础上设计最优相序程序，可以解决三相负荷不均衡问题。

5 总结

该文针对配电网线损问题进行探究，以低压配电网三相负荷不平衡问题作为研究突破口，通过分析低压配电网三相负荷不平衡与用户负荷之间的量化关系，构建三相负荷不平衡优化模型，运用该模型计算当前三相负荷不平衡度。利用MATLAB 软件编写最优相序计算程序。应用结果表明，该文设计的三相负荷不平衡优化模型可以求取三相负荷不平衡度，经过软件程序计算，确定调整方案，该方案能够降低三相负荷不平衡度。