采用多目标粒子群算法的本体元匹配方法*

薛醒思，耿爱峰，BENINE Ramzi

（1.福建工程学院智能信息处理研究中心，福建福州 350118；2.福建技术师范学院大数据与人工智能学院，福建福清 350300；3.太原理工大学电气与动力工程学院，山西太原 030024）

本体是描述概念和概念之间关系的术语，涵盖了相关领域的知识和词汇. 在计算机领域中，它指的是“形式化的，对于共享概念体系的明确而又详细的说明”[1]，通过对概念体系中语义的共同理解和语义网的扩展，可以实现计算机信息系统语义上的互操作.然而，对于不同的本体工程师来说，一个相同领域的本体可能有不同的构建方法，对一个概念的描述可能有不同的方式，这就会引入本体异构的问题[2].本体异构体现在三个方面，分别为系统异构、语法异构和层次异构.解决本体的异构问题是实现语义融合、知识共享的关键，本体匹配技术可以有效地消除语义异质，解决上述问题[3].

本体匹配方法研究如何确定两个异质本体中实体之间的等价关系，大体可以分为两大类，即本体元匹配方法和本体实体匹配方法[4].本体元匹配问题研究的是如何组合和调试不同的相似度度量方法以确定高质量的本体匹配结果，该问题是目前本体匹配领域的研究热点.为求解该问题，本体元匹配方法首先通过相似度度量方法来确定不同的相似度矩阵，然后为这些矩阵赋予合适的权重和阈值来获得最终的匹配结果[5].由于权重和阈值的取值范围是[0,1]的实数，因此本体元匹配问题通常被建模为一类连续优化问题.

粒子群优化算法（particle swarm optimization algorithm, PSO）[6]拥有鲁棒性高、收敛速度快等特点，是目前数值优化领域的主流优化算法之一.PSO 的一些特性使得它适合于求解本体元匹配问题：（1）PSO 可以很容易地调整评估匹配结果的目标函数；（2）由于可以处理大规模的输入，用PSO 来处理大规模本体匹配是相对容易的；（3）PSO 具有高度的潜并行性，有利于提高求解本体元匹配问题的效率[7].本体匹配结果的质量通常可以用两个指标来衡量，即查全率和查准率[8].这两种指标都需要专家事先提供参考匹配结果，然而在实际应用中，这样的匹配结果是不存在的[9].为解决这个问题，提出两个近似的查全率和查准率指标来度量匹配结果的质量.由于这两个指标在一定程度上是矛盾的，因此为本体元匹配问题构建了多目标优化模型以更好地描述该问题的本质.为了求解多目标的本体元匹配问题，进一步提出多目标粒子群算法（multi-objective PSO, MOPSO），以确定帕累托前沿解集.本文的贡献总结如下.

首先为本体元匹配问题建立了一个全新的优化模型，通过优化模型的决策变量为本体元匹配寻找最合适的权重和阈值，从而获得质量最高的匹配结果；其次，提出了MOPSO 对该问题进行求解；最后，将这些方法与国际本体匹配竞赛（Ontology Alignment Evaluation Initiative, OAEI）[10]参与者在benchmark 测试数据集上进行了对比，实验结果发现MOPSO能够更有效地匹配不同异质本体，从而实现跨领域的知识集成.

1 相关概念和定义

1.1 本体和相似度矩阵

本体用来规范化和形式化异构信息，用以解决语义异构和语法异构的问题，是信息互操作的基础.本体由众多实体组成，实体包括代表概念的类、概念之间的关系属性和概念类的实例，可以用一个三元组来表示，即（C,P,I），其中C，P，I分别代表类、属性和实例.图1展示了一个医学本体的例子，其中矩形中的内容代表类，类之间的关系和属性用矩形之间的单向箭头表示，每个类下面可以扩展属于它们的实例.

图1 关于新冠肺炎的医学本体

为了衡量不同本体的实体之间的相似程度，促进语义融合，多种相似度度量技术被提出并运用到本体匹配的过程中.度量实体之间的相似程度需要从三个方面考虑，即语言、语义和结构，因为仅从一个方面来考虑实体的相似度是片面的，缺乏说服力[11].文章用到的三种相似度度量技术在2.1 节中详细介绍. 相似度矩阵由实体间的相似度值组成，如表1 所示，其中O1和O2分别代表两个待匹配的本体，e11,…,e1n代表本体1 中的n个实体，e21,…,e2m代表本体2 中的m个实体，c11,…,cnm代表每对实体对应的相似度值.

表1 相似度矩阵表

1.2 多目标的本体元匹配问题

本体匹配是解决两个本体异质问题的有效方法，通过将具有相等语义关系的实体进行匹配来实现知识的共享和融合，图2 描述了两个异质的本体，图中左右两侧的圆角矩形及其分支分别代表了两个本体中的实体，“≡”代表了两个实体是等价关系，用一个双向箭头连接.这些实体的名称可能是不同的，但是它们所代表的含义可能是相同的，由这些实体组成的两个本体就是异质的.本体元匹配是本体匹配的一种技术，被定义为如何为相似度矩阵确定一组合适的权重和阈值，使得本体匹配结果的质量最高.对于多目标的本体元匹配问题，匹配结果质量的高低由两个目标函数评估，多目标本体元匹配的建模在2.2 节详细说明.本体元匹配的每个权重对应由一种相似度度量方法获得的相似度矩阵，这些相似度矩阵通过权重组合为一个综合相似度矩阵.找到综合相似度矩阵中同时为所在行和列的最大值的元素，该元素所对应的两个实体即被认为是等价的.最后，经过阈值过滤掉置信度低的匹配对，剩下的实体对集合就被认为是一组本体元匹配结果.

图2 两个异质的本体示意图

本体元匹配的流程如图3 所示，其中O1和O2分别代表源本体和目标本体，A是部分匹配结果，R是外部资源（如外部词典），Matching 是匹配过程，P是相关参数，threshold 是阈值，A′是匹配结果.图4 是源本体和目标本体的匹配结果的例子，两个等价的实体通过双向箭头连接.

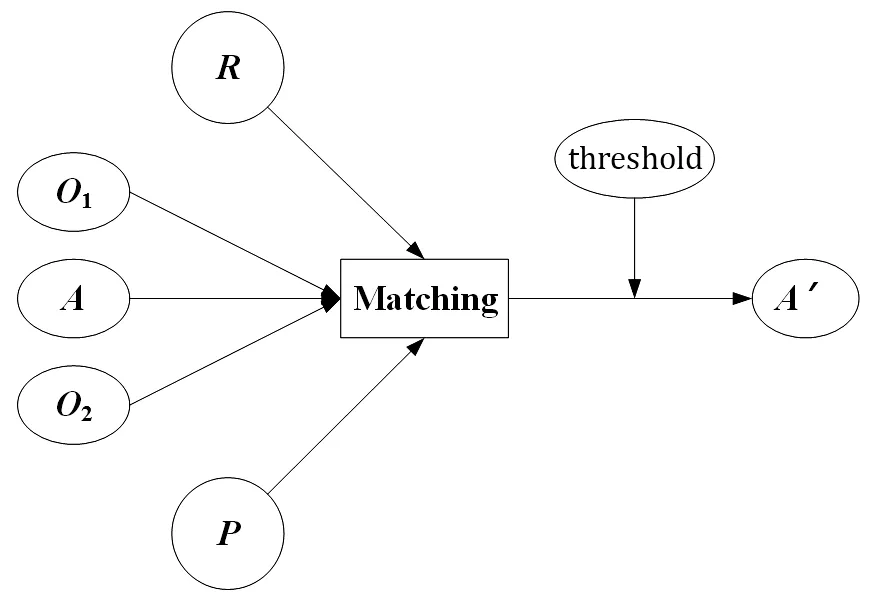
图3 本体元匹配流程图

1.3 多目标优化问题

不同于单目标优化问题一次只优化一个目标，多目标优化问题（multi-objective optimization problem, MOP）需要同时优化两个以上矛盾的目标,该问题的定义如式(1)所示.

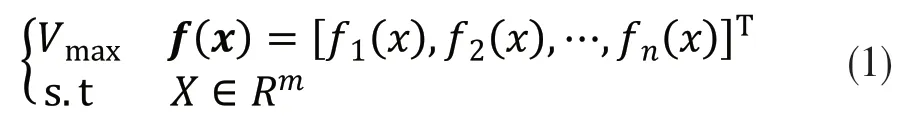
其中：Vmax表示向量极大化，fk(x)(k=1,2,…,n)表示向量目标函数f(x)的子目标，各个子目标向量都尽可能达到最大值；x是问题的解，x∈Rm是多目标优化问题的限制条件和约束.

求解多目标优化问题需要确定一组非支配的解集，解的支配关系定义如下.

1）如果有解x1,x2∈X, 对于任意的k=1,2,…,n，都有fk(x1)＞fk(x2)，则称解x1支配解x2，记为x1≤x2；

2） 如 果 有 解x1,x2∈X对 于 任 意 的k=1,2,…,n，不全有fk(x1)＞fk(x2)，则称解x1与解x2互不支配，记为x1≠x2.

由支配的解集拟合的目标空间的曲线称为帕累托前沿（pareto front, PF），图5 描述了多目标优化问题的帕累托前沿.假设是最大化问题，图中横轴和纵轴分别代表了两个优化目标，实心点代表处于支配地位的非劣解，空心点表示被支配的解，由实心点拟合的曲线表示帕累托前沿.由于帕累托前沿上的解有无穷多个，曲线上的拐点被认为是多目标优化问题的代表解.当帕累托前沿曲线拐点解的一个目标有些许增强时，另一个目标会迅速被削弱，因此拐点解就是潜在的最优解.

图5 多目标优化问题的帕累托前沿

2 基于多目标粒子群算法的本体元匹配方法

2.1 使用的相似度度量技术

文章所使用的三大类相似度度量技术如下.

1）基于语言学的相似度技术N-Gram[12]，其计算公式如下.

其中s1和s2分别是两个字符串，C(s1,s2)是它们的共同子串个数，ns1和ns2分别是两个字符串的长度.

2）基于语义的相似度技术Wu&Palmer[13]，其计算公式如下.

其中depth( )表示字符串所代表的单词在WordNet[14]的层次语义结构中的深度，lcs(s1,s2)是s1和s2最接近的共同父概念.

3）基于结构的相似度技术Out&InDegree，其计算公式如下.

其中e1和e2表示两个待匹配的实体，ns( )代表实体的父子类数量总和.

由上述三种相似度度量方法得到的三个关于待匹配本体的相似度矩阵需要由一组权重集成为一个相似度矩阵，该矩阵被称为综合相似度矩阵，用以得到匹配结果，即实体对的集合.

2.2 多目标本体元匹配优化模型

评价一个匹配结果的质量通常采用的度量指标是查全率(recall)和查准率(precision)，它们的定义如下.

其中R代表由专家给出的标准匹配结果，A代表匹配系统获得的匹配结果.然而在现实中，本体之间的匹配是没有参考结果的，而且对于一些大规模本体来说，参考结果的构建需要很高的成本，近似评估指标的引入可以有效解决这一问题，其应用在本体匹配的优化过程中，用于匹配过程中结果的评估，引导匹配结果向最优方向靠近.文章的两个近似评估指标为approRecall 和approPrecision，分别用来近似评估查全率和查准率，其计算公式分别如下：

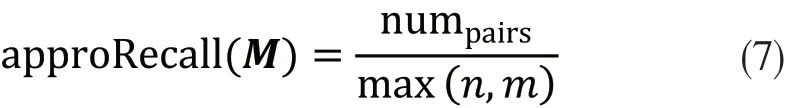
其中，M 为综合相似度矩阵，numpairs表示综合相似度矩阵中所有满足阈值条件且置信度值在所在的行和列中均为最大值的元素对应的实体对个数，n和m分别为源本体和目标本体包含的实体个数.

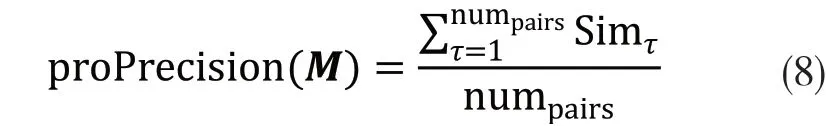
其中，τ为满足阈值条件且置信度值在所在的行和列中均为最大值的元素对应的实体对的索引，Simτ表示上述第τ个实体对的相似度值.

在此基础上，多目标的本体元匹配问题的优化模型定义如下.

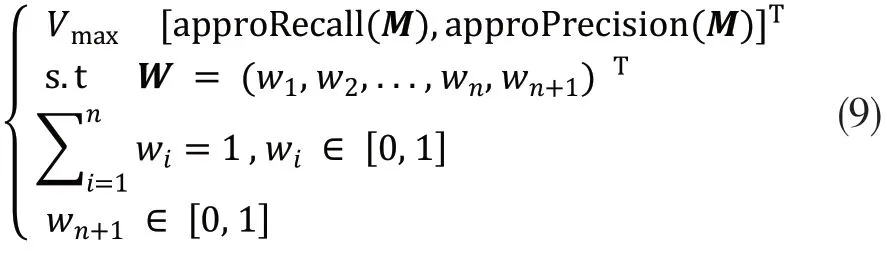
其中，wi(i=1, …,n)代表相似度权重，代表阈值.

2.3 多目标粒子群算法优化本体元匹配的流程

图6给出了用MOPSO 优化本体元匹配模型的流程图. MOPSO 由三个主要部分组成：主函数，外部存储库和变异算子，其中主函数包括外部存储库的更新和变异算子的计算，在图6 中分别用点状和网状阴影标出.它们在优化本体元匹配模型时的描述如下.

图6 多目标粒子群算法优化本体元匹配模型流程图

2.3.1 主函数

主函数包括以下几个步骤：1）初始化种群中粒子的位置，每个位置代表了本体元匹配问题的一种解；2）初始化每个粒子的速度（均为0）和记忆（即个体历史最优解）；3）分别利用公式(2)、(3)、(4)计算三个相似度矩阵，每个粒子通过其位置信息将三个相似度矩阵集成为一个综合相似度矩阵；4）根据综合相似度矩阵和公式(7)、(8)计算种群中每个粒子的两个目标函数值；5）初始化外部存储库，在存储库中存储表示非支配向量的粒子；6）生成搜索空间的超立方体（即将目标函数空间划分为等分的网格）；7）开始迭代，直到满足如下结束条件. a）用公式(10)计算每个粒子的速度，其中i是粒子的索引，w是惯性权重，r1、r2是[0，1]之间的随机数，参数的取值会在3.1 节中说明，pbest[i]是粒子i的历史最优位置，rep[h]是从存储库中选择的粒子的位置，通过轮盘赌的方式首先选择粒子密度最小的超立方体，h是在这个超立方体中随机选择的粒子的索引，pop[i]是当前粒子的位置. b）用公式(11)计算粒子的新位置，保证粒子的位置不超过搜索空间的边界. c）分别利用公式(2)、(3)、(4)计算三个相似度矩阵，将三个相似度矩阵集成为一个综合相似度矩阵. d）用公式(7)、(8)计算每个粒子新的目标函数值. e）根据支配关系更新存储库中的内容以及网格内的粒子的位置表示，当存储库被填满时，目标空间中密度低的网格中的粒子被优先保存. f）根据粒子的两个目标函数值更新粒子的记忆解. g）循环次数加1；8）满足结束条件时结束循环.

2.3.2 外部存储库

外部存储库用来存储搜索过程中发现的非劣解，由归档控制器和网格（超立方体）组成.

1）归档控制器.决定是否应该将某个解添加到存储库中：如果a）存储库为空，新解直接加入到存储库；b）存储库不为空，新解被存储库中的解支配，则丢弃新解；c）存储库不为空，新解与存储库中的解互不支配，则将新解加入到存储库中；d）存储库不为空，新解支配存储库中的解，则用新解取代存储库中被新解支配的解；e）存储库已满，则自适应调整网格.

2）网格.用网格将目标函数空间划分为各个区域，如果加入的新解在当前网格的边界外则必须重新计算网格.

2.3.3 变异算子

文章采用的变异算子[15]是一个非线性的函数，代表变异的范围.在迭代开始时所有的粒子都进行变异操作，之后迅速减小变异粒子的数量（相对于迭代次数而言），即随着时间的推移变异的范围逐渐缩小，种群最终趋于收敛.这种变异操作不仅作用于粒子，同时还作用于粒子的各个维度.变异算子range 由公式(12)确定.

其中currgen 表示当前迭代次数，totgen 为迭代总数，即变异率.

3 实验

3.1 实验配置

国际竞赛OAEI 致力于评估各种本体对齐算法的性能.文章采用OAEI 提供的benchmark数据集，通过5 类不同的异质本体匹配任务来测试MOPSO 的性能.表2 给出了OAEI 的benchmark 数据集的相关描述.

表2 OAEI 的benchmark 测试本体的相关描述

将MOPSO 的结果同OAEI 上的参与者AML, edna, LogMap, LogMapLt, XMap 和LogMapBio 进行比较，表3 和表4 给出了实验结果，用无参考匹配方法得到的匹配结果与这些参与者的结果都统一用公式(5)和(6)的recall 和precision 指标来评估.其中，MOPSO的实验结果是算法独立运行30 次的平均值.

表3 OAEI 的参与者与本文方法在benchmark 轨道上的recall 值比较

表4 OAEI 的参与者与本文方法在benchmark 轨道上的precision 值比较

MOPSO 的参数配置如下：其中包括惯性权重，学习因子和，种群规模，迭代次数，网格等分数量，存储库阈值和变异率.其中惯性权重和变异率采用文献[15]给出的数值，分别为0.4 和0.5，经过实验测试，改变惯性权重和变异率的数值，得到的匹配结果的质量均未能优于当两个参数分别为0.4 和0.5 时.其他的参数经过参数敏感性实验得到的参数配置结果如表5 所示.

表5 MOPSO 的参数配置

3.2 实验结果与分析

从表3 和表4 中可以看出：

1）101～104. 对于这些测试用例,先进的OAEI 系统都能够实现它们的最大目标值,包括LogMapLt 和LogMapBio, 可以解释为在这些本体中, 词法、语义和结构信息的类和属性不是异质的, 基于词法、语义和结构的匹配器都可以有效地匹配这些本体.

2）201～210. 这些本体具有相同的结构特征和不同的词汇及语义特征.因此，基于更有效的词汇和语义匹配器的匹配系统在这些测试用例中表现良好.由表3 和表4 可以看出，由于本方法更好地结合了基于词汇、语义和结构的匹配器，并进行了适当的预处理，所以本方法的目标平均值明显优于其他的OAEI 参与者,只是在查准率上略低于AML.

3）221～247. 由表3 和表4 可以看出，本方法和edna在recall目标上取得了最好的结果，而与AML 在precision 目标上的结果优于其他匹配系统.因为这些测试本体具有相同的词汇和语义特征，但结构特征不同，因此对基于结构的匹配器要求较高.本方法通过减少结构匹配器的权值来获得更好的匹配结果.

4）248～266. 这些本体的特征在词汇、语义和结构上都不同，即本体之间的异质性非常高，很难得到满意的匹配结果.由表3 和表4可以看出，本方法在recall 目标上相对于OAEI的其他先进系统具有显著优势.同时，这些匹配系统在这些测试用例中性能较差，原因如下:虽然本方法使用的匹配器可以有效地结合词汇、语义和结构匹配器，但这些本体的词汇、语义和结构信息被完全打乱，从而降低了最终匹配结果的质量.在这些测试案例中，本方法的结果是可以接受的.

5）301～304. 这些本体来自现实世界，由不同的本体工程师构建，OAEI 的参与者没有测试这些测试用例.

4 结论

本体匹配是实例共享、查询重写、本体集成、辅助翻译等应用的基础，可以实现知识的融合与信息的交互.对于匹配问题来说，相似度度量方法的选择是关键，如何集成多种度量方法以获得最优的本体匹配结果是本体元匹配问题的核心. 本体匹配结果质量的高低需要两个目标来评估，为了避免专家构造标准匹配结果的不便，两个近似评估指标被提出来代替传统的查全率和查准率.为了获得高质量的匹配结果，首先将本体元匹配问题建模为多目标优化问题，目标函数为近似查全率和近似查准率；其次，通过一个加入变异算子的MOPSO 来优化这两个目标函数，MOPSO 具有收敛速度快，粒子并行探索的特征，适合于解决本体匹配问题；最后，将MOPSO 的寻优结果输出，即找到一组最合适的权重和阈值.在实验阶段，本方法通过与OAEI 的参与者在benchmark 测试集上进行结果比较来证明其有效性.实验结果表明，本方法比其他的参与者在两个目标上都具有优势，这说明本方法可以有效地结合不同特征的相似度度量方法，有助于更好地实现本体融合.

如何选择和集成相似度度量技术仍然是本体元匹配面临的主要挑战之一，在未来的工作中，更准确、更合适的相似度度量技术需要被发掘和应用.另一方面，MOPSO 也需要进一步改进来克服早熟收敛的问题，在其他的测试数据集上，MOPSO 的性能还需被进一步验证，未来会将MOPSO 应用于求解大规模本体匹配的问题中，MOPSO 快速的收敛速度对于解决此类问题会有帮助.