基于偏正态概率分布的粒度分布次总体分离及其沉积环境指示意义

袁瑞，张昌民，赵芸，张莉，陈哲，张宝进，黄若鑫

1) 长江大学地球物理与石油资源学院，武汉，430100；2) 长江大学地球科学学院，武汉，430100；3) 成都北方石油勘探开发技术有限公司，成都，610051；4) 中国石化江汉油田分公司，湖北潜江，433124；5) 中海油田服务股份有限公司油田技术事业部，北京，101149

内容提要:沉积物颗粒是某种沉积环境和水动力条件下多个沉积过程的最终产物。粒度分布是原始沉积信息的载体，是来自不同沉积过程的多个次总体的叠加，频率曲线可能表现为双峰或者多峰特征。传统的沉积学粒度分析方法并未深入研究次总体；常见的概率分布模型在分离次总体后无法全面计算统计参数。本文以214份鄱阳湖现代沉积物的粒度分布数据为例，利用偏正态概率分布模型共分离提取977个次总体，计算各个次总体的统计参数，并对比分析了不同沉积环境中次总体参数的异同。结果表明：① 次总体均值、方差、偏度、峰度、所占百分比和最大频率等参数规律明显；② 从曲流河河道到河流末端、在河流末端顺流方向上和河道左右两侧远离河道方向上，粒度分布中主要次总体粒度均值逐渐减小，河道间洼地和湖区沉积物粒度分布的各个次总体占比接近；③ 江心洲的河道砂和河漫滩细粒粒度分布分别由3种和5种不同类型次总体组成。该方法可为沉积环境的定量判断和沉积过程的定量研究提供参考。

碎屑沉积物的粒度是地球科学最早研究的对象之一，也是沉积学和地质学研究使用最广泛的数据(Udden,1914;Krumbein,1934;Bright et al.,2020)。由不同大小颗粒体积或重量百分比组成的粒度分布(Grain-Size Distribution,GSD)记录了沉积物原始沉积信息，粒度分布不仅是研究现代沉积环境的有力证据、推断古气候和古环境的最常用的数据资料(IJmker et al.,2012;Vandenberghe,2013;Rose et al.,2019;Bright et al.,2020;Zhang Xiaodong et al.,2020;王中波等,2020)，更是母岩风化序列的“指纹”(Román-Sánchez et al.,2021)。为了挖掘这些隐藏的信息，Krumbein(1934)创造性将粒度分布的自然刻度转换为以2为底的对数φ刻度。根据粒度频率曲线、累积曲线和概率累积曲线的形态定性、或者结合图解法与矩法公式计算的粒度分布参数(均值、中值、方差、偏度和峰度)和CM图版半定量分析沉积环境(Krumbein and Pettijohn,1938;Folk and Ward,1957;Visher,1969;Passega,1964;Blott and Pye,2001)。在获得一定数量的粒度分布数据后，众多非传统沉积学手段也得到了广泛的应用。多重分形(Multifractal)方法根据粒度频率曲线的形态，利用分形理论得到的奇异谱代表不同沉积环境(Posadas et al.,2001;Paz-Ferreiro et al.,2010;Biswas,2019;常宏等,2019;Li Jinlin et al.,2021;Qiao Jiangbo et al.,2021)；聚类算法(Clustering Algorithm)根据粒度分布参数或粒度频率曲线形态的相似性判别沉积环境(Ordóez et al.,2016;章婷曦等,2018;刘祥奇等,2020)；端元模型(End Member)分析方法根据预先设定的端元，从粒度分布频率曲线中寻找对应的沉积过程和沉积环境指标(Weltje,1997;Weltje and Prins,2007;IJmker et al.,2012;Hateren et al.,2018;Zhang Xiaodong et al.,2020;李洋等,2020;梁爱民等,2020)。

砾质河床上砾石在强水流的驱动下沿河床滚动堆积而形成开放结构砾石，当水动力减弱时，早期支撑砾石之间的孔隙才被后期的细粒沉积物充填(Carling,1984;Wooster et al.,2008;Herrero and Berni,2016;张昌民等,2020)。细粒物质在较粗颗粒间通过多次渗滤作用形成了最终的疏松沉积物，每一次渗滤过程对应了沉积水动力的变化(Gibson et al.,2011;张昌民等,2020)。通过实验和数值模拟，多期沉积过程在砂岩骨架中也得以被证实(Khullar and Raju,2017;Bustamante-Penagos and Nio,2020)。最终沉积物的粒度分布是来自不同沉积过程的多个次总体(Subpopulation)的叠加(Gan and Scholz,2017;Wu Li et al.,2020)，并在粒度频率曲线中表现为双峰或者多峰特征(Kuhnle,1993)。这些粒度分布次总体是沉积物的最小结构单元，具有沉积“基因”的意义(Weltje and Prins,2007;Hateren et al.,2018)。

传统沉积学中滚动、跳跃和悬浮三段式的粒度分布概率累积曲线形态显然无法分离、提取与沉积过程相关的粒度分布次总体。粒度分布数据本质上即为统计数据体。为了从数学上分离、提取这些与沉积水动力条件、沉积过程和沉积环境有关的粒度分布次总体，许多概率统计分布模型被应用于粒度频率曲线的分解，例如对数正态(Log Normal)分布(Spencer,1963;Xiao Jule et al.,2012)、Rosin分布(Kittleman,1964;Ibbeken,1983)、对数双曲(Log Hyperbolic)分布(Bader,1970;Purkait,2002;Bartholdy et al.,2007)、Weibull分布(Carder et al.,1971;Kondolf and Adhikari,2000;Wu Li et al.,2020)、对数偏拉普拉斯(Log Skew Laplace)分布(Fieller et al.,1992;Purkait,2002)和伽马(Gamma)分布(Risovic,1993)等。但是这些概率分布从原理上无法或较难计算偏度这一重要参数。偏正态(Skew Normal)概率分布在正态分布的基础上引入形状参数，可便捷地计算各个次总体的均值、方差、偏度和峰度(Azzalini,1985,2005;Gupta and Chen,2001;Ashour and Abdel-hameed,2010;Yalçnkaya et al.,2018)。本文以214份鄱阳湖现代沉积物粒度分布数据为例，采用偏正态概率分布分离、提取各个粒度分布中的次总体，计算次总体的统计参数，分析这些参数在不同沉积微相中的内在联系与差异，并探讨次总体对沉积环境的指示意义。

1 数据来源

1.1 取样位置

鄱阳湖(28°22′～29°45′N，115°47′～116°45′E)是我国最大的淡水湖泊，其水域主要是五大曲流河(赣江、抚河、信江、饶河、修河)与下泄长江的水量吞吐动态平衡的结果，流域内的泥沙沉积物对流域环境有特殊的启示意义(纪伟涛等,2017;甘建军等,2019;万智巍等,2020)。五大河流中，赣江水系最为发育，分为四大分支：赣江西(主)支、北支、中支和南支(图1a)(纪伟涛等,2017)。赣江西支向北与修水合并后消亡于入湖水道；赣江北支与中支汇合后入湖形成赣江三角洲沉积；赣江南支与抚河和信江汇入康山河，向北流入鄱阳湖，形成狭长的康山河三角洲沉积。每年4～9月汛期，五大河流以及独流小河河水入湖，湖水上涨，湖面扩大；冬春枯水季节，流水减少，湖面变小，三角洲前缘显露，呈现出“枯水一线，洪水一片”的特殊地质现象(纪伟涛等,2017)。本文主要数据来源为枯水期的赣江曲流河、赣江三角洲、康山河三角洲和湖泊沉积，2019年12月3日～9日在20个位置的表层及探槽中共采集214个现代沉积物样品，沉积环境包括曲流河河道、曲流河河漫滩、三角洲平原分流河道、天然堤、河道末端、河道间洼地以及湖泊等(张金亮,2019;马鹏飞等,2021;张宪国等,2021)(图1a)。

图1 鄱阳湖流域概况及沉积物取样位置Fig.1 General drainage situation of the Poyang Lake and sampling locations of sediments(a) 鄱阳湖流域及本文20个取样位置；(b) 康山河末端取样位置；(c) 康山河江心洲取样位置(a) Drainage of the Poyang Lake and 20 sampling locations;(b) sampling locations in the terminal of the Kangshan River;(c) sampling locations in the central bar of the Kangshan River

1.2 粒度分析实验

在粒度分析前，取适量沉积物样品，分别加入双氧水和稀盐酸进行前处理，去除有机质和自生碳酸盐物质，然后用蒸馏水进行离心清洗。少数含砾沉积物样品采用筛析法(0.25φ间隔)，形成粒径大于2000 μm部分的粒度分布。无砾沉积物样品粒度分析工作在美国贝克曼库尔特公司的LS13 320激光粒度分析仪(理论测量范围0.017～2000 μm)上完成，设置粒度测试区间为0.375～2000 μm(11.38～-1φ)，粒径间隔0.135φ。对每一份样品重复测试至少3次颗粒体积比，相对误差小于2%后取3次测试结果的平均值作为该样品的粒级数据。最后利用粒度分析仪自带仿真程序将粒径大于2000 μm部分和小于2000 μm部分的粒级数据合并，形成完整的粒度分布数据(图2a)。利用矩法公式计算各个粒度分布数据的均值、中值、方差、偏度和峰度。

图2 鄱阳湖沉积物214个粒度分布热图(a)及其977个次总体频率热图(b)Fig.2 Frequency heat maps of 214 grain-size distributions (a) and 977 subpopulations (b)

2 研究方法

2.1 偏正态概率分布

1985年，意大利数学家Azzalini在正态概率分布中添加了形状参数，首先提出了偏正态概率分布的数学原理。设随机变量Y服从偏正态概率分布Y～SN(μ,σ2,α)，其中μ为位置参数，σ≥0为尺度参数，分别与正态分布N(μ,σ2)中的μ(也称为均值)，σ(也称为标准差)含义一致，α为形状参数(Azzalini,1985,2005)。与其他概率分布模型相比，正是因为偏正态概率分布模型中包含了形状参数α，才使得偏正态分布概率密度函数可以直接计算偏度与峰度。偏正态分布概率密度函数为(Azzalini,1985;Yalçnkaya et al.,2018)：

(1)

随机变量的均值M、方差V、偏度Sk和峰度Ku为(Gan and Scholz,2017;Yuan Rui et al.,2018)：

(2)

其中

特别地，当α=0时，M=μ，V=σ2，Sk=Ku=0即为正态分布N(μ,σ2)。

2.2 粒度分布的偏正态概率分布模型

受多期沉积过程的影响，沉积物粒度分布Y由多个次总体Yi组成。设粒度分布次总体Yi均服从偏正态概率分布Yi～SN(μi,σi2,αi)，其中μi、σi和αi分别为第i个次总体的位置参数、尺度参数和偏度参数，则沉积物粒度分布的偏正态概率分布模型为(Gan and Scholz,2017;Yuan Rui et al.,2018)：

(3)

其中ci为第i个次总体的所占百分比，∑ci=100%；x为粒径；粒度分布中某个粒径的频率y的估计值为各次总体频率之和∑yi。采用自适应网格最优化求解得出每个次总体的偏正态概率分布模型参数(ci,μi,σi2,αi)，再利用公式(2)计算各个次总体的均值、方差、偏度和峰度。本文把粒度分布中占主导、所占百分比明显最大的次总体称为主要次总体。

3 计算结果

3.1 次总体分离

多期沉积过程中形成的沉积物在粒度频率曲线中表现为双峰或者多峰特征，若每一个峰值对应一个次总体，则可以利用偏正态概率分布从粒度分布中分离各个次总体。逐个对214个沉积物粒度分布数据进行处理，单个粒度分布的次总体个数为2～7个，共分离出977个次总体(图2b)，计算每个次总体的所占百分比、均值、方差、偏度、峰度和最大频率(次总体中的峰值频率)。例如，1个现代沉积物样品的粒度分布及其次总体计算结果如图3所示。该样品取自康山河枯水主河道中部，野外鉴定为粉砂质泥，其粒度频率曲线具有为5个峰值。利用偏正态概率分布从中共分离出6个次总体，由粗到细，这些次总体在粒度分布中所占百分比依次为38.02%、4.13%、16.31%、15.46%、20.04%和3.6%，次总体的均值分别为0.75φ、1.74φ、2.60φ、4.52φ、6.79φ和8.70φ，方差分别为0.16、0.07、0.16、0.37、1.22和0.44，偏度分别为-0.44、0.00、0.37、-0.75、-0.84和0.00，峰度分别为0.30、0.00、0.23、0.60、0.69和0.00，最大频率分别为5.24%、0.86%、2.21%、1.49%、1.09%和0.29%。次总体S1所占百分比最大，为该粒度分布的主要次总体。各个次总体总和即为粒度分布的拟合，214个粒度分布拟合的绝对误差均不超过2%。

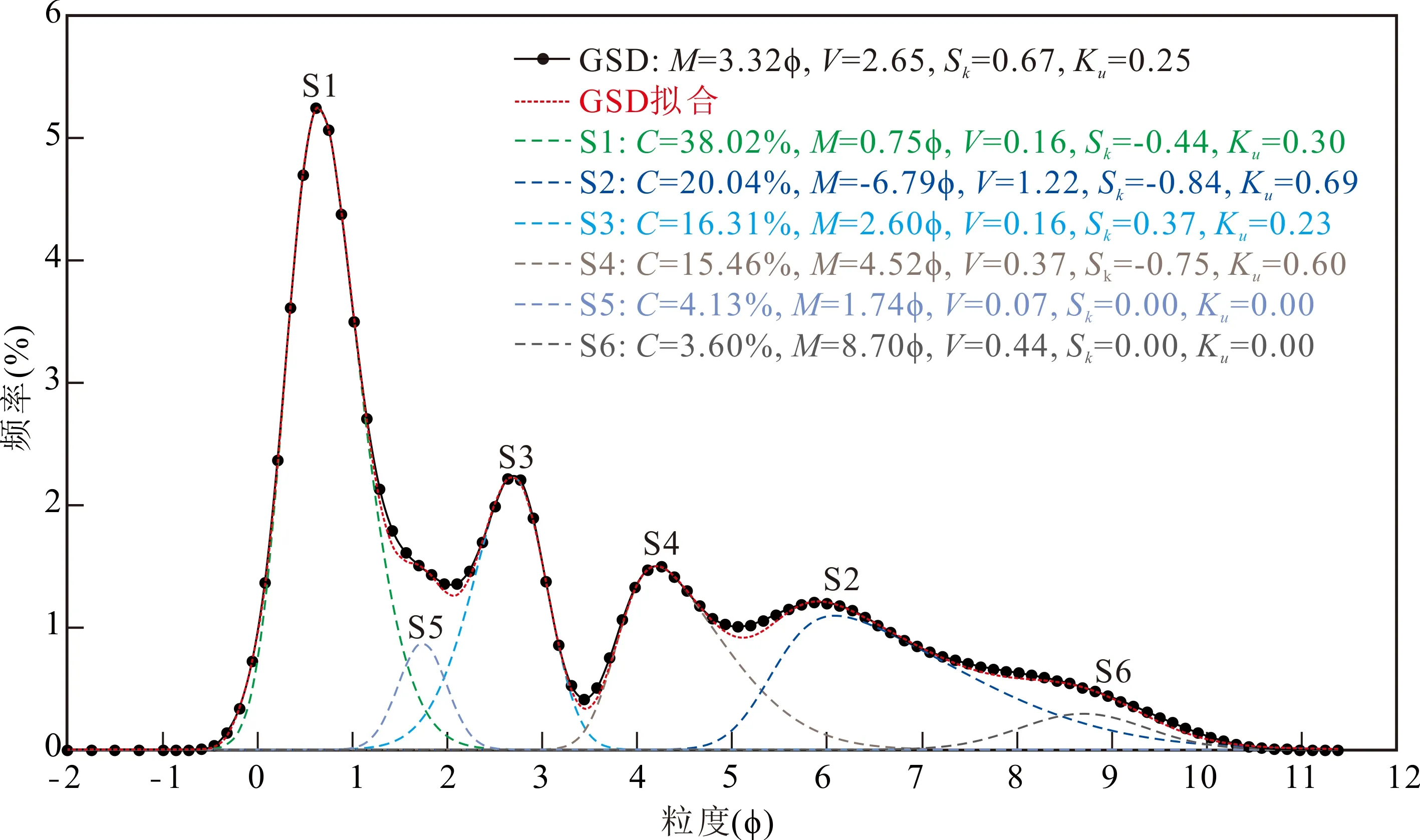
图3 康山河沉积物中1个粒度分布及其6个次总体与参数Fig.3 One grain-size distribution and its six subpopulations and parameters

3.2 次总体参数特征

对本次所有977个次总体的均值、方差、偏度、峰度、所占百分比和最大频率进行统计，发现这些次总体的统计参数既存在相似性也存在差异性。次总体均值主要集中在6个区间上：0～1φ、1～2φ、2～3φ、4～5φ、6～7φ和7～8φ，根据Friedman和Sanders (1978)岩石粒径划分标准，分别对应了粗砂、中砂、细砂、极粗粉砂、中粉砂和细粉砂组分；样品中含砾(<-1φ)、极粗砂(-1～0φ)、极细砂(3～4φ)和粗粉砂(5～6φ)组分较少，泥质组分主要包含在细粉砂次总体中(图4a)。

根据Folk和Ward (1957)分选性等级划分标准，次总体中粗砂(0～1φ)和中砂(1～2φ)组分的分选性主要为极好；细砂(2～3φ)组分的分选性主要为极好—好；极粗粉砂(4～5φ)组分分选性为极好—较好；中—细粉砂(6～8φ)组分的分选性与均值负线性关系明显(方差=1.1136φ-6.3437，R2=0.8829)，均值越小，分选性越差(图4b)。根据Folk和Ward (1957)偏度等级划分标准，次总体粗砂(0～1φ)组分偏度分布范围较大；中砂(1～2φ)和细砂(2～3φ)组分主要为粗偏—极细偏；由于泥质组分的存在，极粗粉砂(4～5φ)、中粉砂(6～7φ)和细粉砂(7～8φ)组分主要为极粗偏(图4c)。

各个次总体的偏度均小于0.8，频率曲线峰态一般较宽(图4d)。粗砂(0～1φ)、中砂(1～2φ)、细砂(2～3φ)组分所占百分比分布区间较大，其中单个次总体组分所占百分比大于60%的样品分选性较好(图4e)。尽管极粗粉砂(4～5φ)和中—细粉砂(6～8φ)组分的次总体粒径频率值小，但是其分选性差，分布区间大，在粒度分布中的百分比仍可达到20%，但一般不超过30%(图4e)。所有次总体的峰值频率均不超过12%；极粗粉砂(4～5φ)和中—细粉砂(6～8φ)组分最大峰值频率分别小于3%和2%(图4f)。

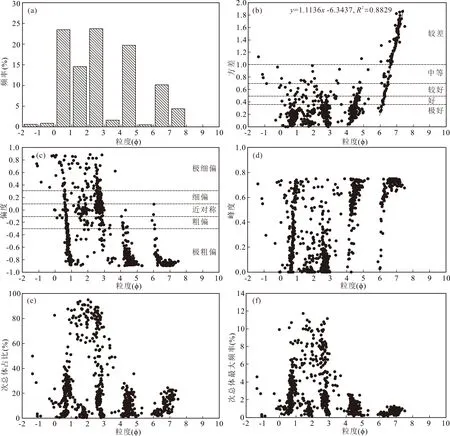
图4 鄱阳湖沉积物977个次总体参数特征Fig.4 Parameter characteristics of 977 subpopulations(a) 次总体均值直方图；(b) 次总体均值与方差交会图；(c) 次总体均值与偏度交会图；(d) 次总体均值与峰度交会图；(e) 次总体均值与所占百分比交会图；(f) 次总体均值与最大频率交会图(a) Histogram of subpopulation means;(b) crossplot of subpopulation means and sortings;(c) crossplot of subpopulation means and skewness;(d) crossplot of subpopulation means and kurtosis;(e) crossplot of subpopulation means and percentages;(f) crossplot of subpopulation means and maximum frequencies

根据不同均值次总体的最大频率与其在粒度分布中所占百分比的交会图可知，次总体所占百分比与最大频率呈线性正相关关系：①当次总体粒度均值为0～1φ时，所占百分比=8.1027×最大频率-2.3106 (R2=0.7660)；②当次总体粒度均值为1～2φ时，所占百分比=10.103×最大频率-1.8329 (R2=0.8801)；③当次总体粒度均值为2～3φ时，所占百分比=9.6316×最大频率-2.1002 (R2=0.9157)；④当次总体粒度均值为4～5φ时，所占百分比=11.545×最大频率-1.6888 (R2=0.9044)；⑤当次总体粒度均值为6～8φ时，所占百分比=22.931×最大频率-2.8404 (R2=0.9444)(图5)。次总体均值越小，线性关系越明显。因此，根据粒度分布中波峰的频率和位置，选取合适的经验公式，可以快速预测该波峰对应的次总体在粒度分布中所占比重。

图5 不同均值次总体最大频率与所占百分比交会图Fig.5 Crossplot of maximum frequencies and percentages of subpopulation within different means

4 沉积环境指示

4.1 不同沉积环境中次总体特征

本次现代沉积物取样环境涉及曲流河、三角洲和湖泊3种沉积相，其中曲流河相包括河道和河漫滩微相，三角洲相包括上平原和下平原分流河道、天然堤、河道间洼地和河流末端等微相(张金亮,2019;马鹏飞等,2021;张宪国等,2021)，湖泊沉积物主要来自于靠近康山河地区的湖区裸露地带。

曲流河河道沉积物粒度分布的次总体主要以粗砂(0～1φ)和中砂(1～2φ)组分为主，少量细砾组分，粗砂(0～1φ)和中砂(1～2φ)组分所占百分比一般大于60%，分选性主要为较好—中等(方差大于0.4)(图6a)。曲流河河漫滩沉积物受到风力的改造，粒度分布频率曲线为单峰，次总体组分主要为中砂(1～2φ)和细砂(2～3φ)，峰值频率接近10%，所占百分比可高达90%以上，分选极好；所含的极少数粗砂和粉砂组分所占百分比一般小于5%(图6b)。三角洲上平原分流河道沉积物粒度分布中主要包含3～4个次总体，中—细砂(1.5～2.5φ)为主要组分，包含少量细砾和粉砂组分；在粒度分布中主要次总体所占百分比约80%左右，分选好(图6c)。与上平原分流河道相比，三角洲下平原分流河道的次总体个数也为3～4个，但是主要组分为细砂(2～3φ)；同时粒度分布中包含有约3%的极粗粉砂(4～5φ)组分(图6d)。

河流末端河道沉积物粒度分布的方差较大(大于2)，粒度分布主要包含4～5个次总体，每个次总体在粒度分布中的所占百分比均小于50%，最大粒度频率一般小于7%；主要次总体的粒度为细—极细砂(2.5～3.5φ)，呈极粗偏的形态(图6e)。在河道间洼地和湖区取样的沉积物粒度分布的均值约为3φ，方差一般大于2.5；次总体个数一般为5～7个，每个次总体在粒度分布中的所占百分比接近(均不超过30%)，最大粒度频率小于5%，无明显占主导地位的次总体；中—细粉砂(6～8φ)的偏度均小于-0.7(图6f)。

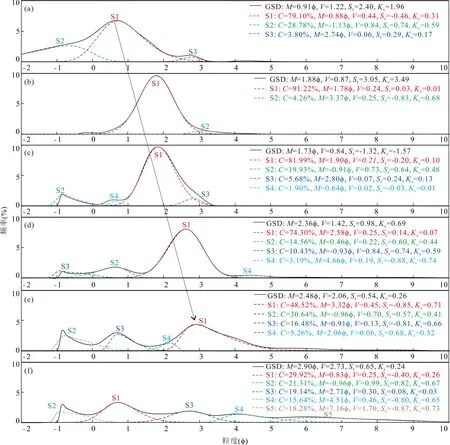
图6 不同沉积环境中沉积物的粒度分布次总体Fig.6 GSD subpopulations of sediments in different sedimentary environments(a) 赣江曲流河河道样品；(b) 赣江曲流河河漫滩上被改造为风成波痕沙丘样品；(c) 赣江三角洲上平原分流河道样品；(d) 康山河三角洲下平原分流河道样品；(e) 康山河末端河道样品；(f) 湖区样品(a) Sample in the channel of the meandering Ganjiang River;(b) sample in the floodplain of the meandering Ganjiang River,which is transformed to be wind-rippled dunes;(c) sample in the distributary channel of the Ganjiang delta upper plain;(d) sample in the distributary channel of the Kangshan River delta lower plain;(e) sample in the channel terminal of the Kangshan River;(f) sample in lake center

对比不同沉积环境中的粒度分布次总体的特征，发现各个微相的粒度分布次总体的差异明显，相应的次总体参数特征见表1。整体而言，从曲流河到河流末端，粒度分布中主要次总体粒度均值逐渐减小，最大频率大于2%的次总体个数逐渐增多。但是河道间洼地和湖区的沉积物表现为河湖共同沉积的特征(王军等,2017;甘建军等,2019;杨超等,2021)，粒度分布的方差大，各个次总体占比接近，无明显的主要次总体，其中细粒组分极粗偏严重。

表1 不同沉积环境中沉积物的粒度分布次总体参数特征Table 1 Parameter characteristics of GSD subpopulations from sediments in different sedimentary environments

4.2 河流末端沉积物次总体差异

河流末端由于水流流量的减小，沿河道水流能量不断损失，河流没有能力再搬运沉积物，最终河流终止。本次在康山河末端顺河道取样8个；在河流消亡处左右两侧的河道、天然堤、天然堤外缘和靠湖区分别取样4次(图1b)。在顺河道方向和左右两侧远离河道方向上，利用矩法公式计算得到各个粒度分布的均值并没有明显减小的规律(图7)。利用偏正态概率分布模型，分离提取次总体后发现，样品L20-8至样品L20-2中所占百分比大于40%、最大粒度频率大于4%的主要次总体的粒度均值由0.70φ逐渐减小至3.32φ；样品L20-1各个次总体所占百分比和最大频率接近，没有占主导的次总体，主要表现为湖区沉积物的粒度分布次总体的特征(图7a)。

左侧远离河道方向上，沉积物的粒度分布主要次总体的粒度均值由0.73φ逐渐减小到3.20φ；天然堤L20-L2和天然堤外缘L20-L3样品的粒度分布为单峰形态，主要次总体所占百分比分别为79.63%和79.86%，指示了被风改造的环境特征(图7b)。在河道右侧，样品L20-R1至样品L20-R3的粒度分布主要为双峰，对应的所占百分比均大于25%；主要次总体粒度均值由2.58φ逐渐减小到2.84φ；最远处样品L20-R4无主要次总体，多个次总体所占百分比接近(图7c)。

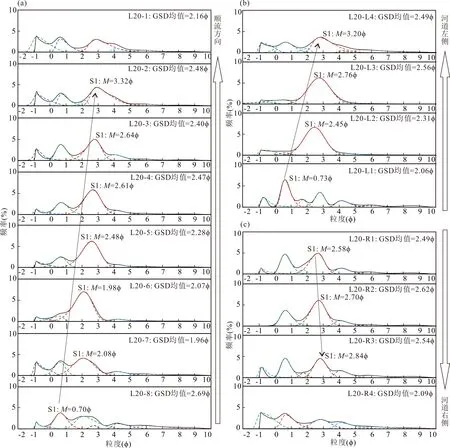
图7 康山河末端不同位置沉积物的粒度分布次总体Fig.7 GSD subpopulations of sediments in different location of the terminal of the Kangshan River(a) 顺河流方向上沉积物粒度分布次总体；(b)河道左侧沉积物粒度分布次总体；(c)河道右侧沉积物粒度分布次总体(a) GSD subpopulations of sediments downstream in channel;(b) GSD subpopulations of sediments in channel left;(c) GSD subpopulations of sediments in channel right

因此，尽管粒度分布的参数无法表征河流终端沉积物粒度的变化规律，但是通过分离得到的次总体参数发现，离河道越远，主要次总体的粒度均值逐渐较小，最终转化为各个次总体的百分比接近、无主要次总体的特征。

5 讨论

5.1 江心洲沉积物次总体组合模式

曲流河江心洲的形成演化受控于泥沙与河流流水交互作用，其在洪水期快速加积、平水期缓慢侧积交替，在洪水期末漫溢的洪水在其表面沉积细粒物质，因此江心洲沉积物包括河道砂与河漫滩细粒(马鹏飞等,2021;张宪国等,2021)。本次取样在康山河分叉口江心洲8个不同位置的浅层探槽处取样5～11次，共取得沉积物66份(图1c)。根据取样剖面的粒度和沉积构造，判断沉积物主要来源于2种沉积环境：①以交错层理为主的河道砂；②以块状层理为主的河漫滩泥质粉砂和粉砂质泥。这两者的沉积物粒度分布数据特点差异明显，河道砂的粒度频率曲线主要以双峰为主，其中1个波峰频率值大；河漫滩细粒的粒度频率曲线主要以多峰为主，没有相对较大的峰值频率(图8)。

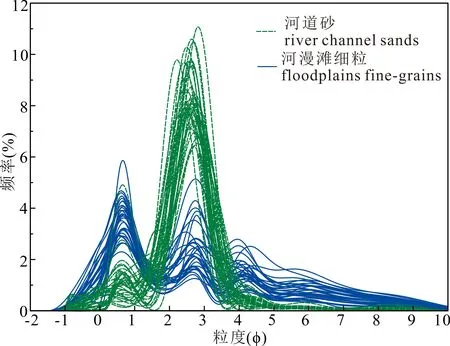
图8 66份康山河江心洲沉积物粒度分布数据Fig.8 GSD data of 66 sediments from the central bar of the Kangshan River

利用偏正态分布共分离得到231个次总体，根据次总体的均值、所占百分比和最大频率的特征，将次总体归纳为8种类型(图9、表2)。河道砂粒度分布由T1、T5和T6次总体类型组成，T5次总体在粒度分布中占主导，所占百分比超过60%，最大粒度频率介于6%～11%之间；T1次总体占比其次，最大频率一般小于2%；T6次总体占比最小，最大频率一般小于1%。河漫滩细粒粒度分布主要由T2、T3、T4、T7和T8次总体类型组成，各个次总体的所占百分比一般不超过40%，最大频率不超过5%；T3次总体主要隐含于T2和T4之间，所占百分比及最大频率均较小；T8次总体多为极粗偏、宽峰度形态。

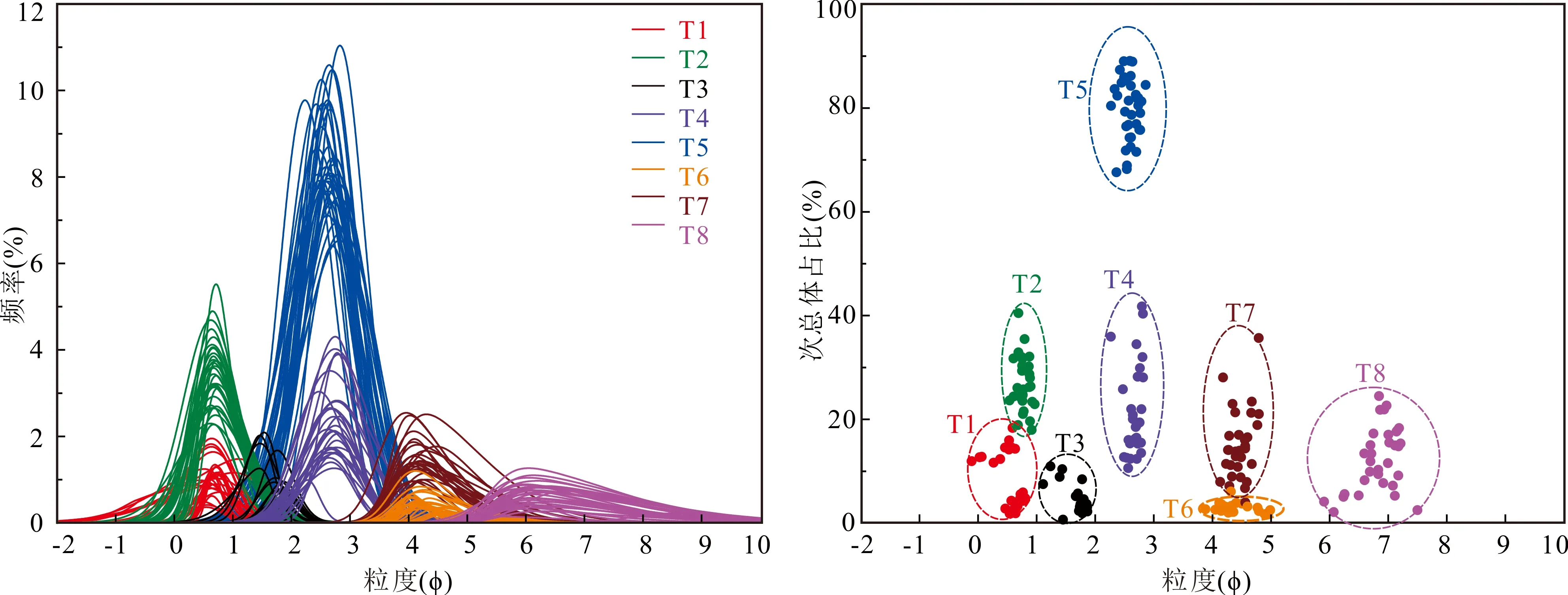
图9 康山河江心洲沉积物次总体参数特征Fig.9 Parameter characteristics of GSD subpopulations from sediments in the central bar of the Kangshan River

表2 康山河江心洲沉积物次总体不同类型Table 2 Different types of subpopulations from sediments in the central bar of the Kangshan River

5.2 不同搬运方式次总体定量化

利用粒度分布分析沉积物的搬运方式时，常用的方法是根据粒度分布概率累积曲线形态划分滚动、跳跃和悬浮次总体(Visher,1969)。但是这种方法无法定量计算各个次总体在粒度分布中的所占百分比。结合偏正态分布分离的次总体及其参数，可以定量研究沉积物的搬运方式和沉积过程。例如，根据一份来自赣江三角洲下平原分流河道沉积物的粒度分布概率累积曲线可知，该沉积物包含跳跃和悬浮次总体，不包括滚动组分(图10)。其中跳跃次总体分为2个直线段，这一特点可能是由河道冲流和局部回流两种沉积造成的(Visher,1969)。第一个跳跃段对应了占比为18.0%、粒度为0～1.5φ、方差为0.12的组分，第二个跳跃段对应了占比为67.6%、粒度为1.5～3.5φ、方差为0.22的组分。前者粒度较粗，分选性更好，代表了较强水动力的冲流沉积，后者粒度稍细，分选性较差，暗示了河道局部回流沉积。悬浮次总体包含了粒度分别为4～5φ、5.5～6.5φ和8～9φ、方差分别为0.15、0.36和0.46的3个组分；粒度越小的组分，分选性越差，代表的水动力越弱(图10)。尽管在粒度分布概率累积曲线中悬浮段对应的线段较长，但是3个悬浮组分占比均小于4%、最大频率均小于1%，其总体含量小，搬运沉积物的水动力整体较强。因此，对粒度分布进行分离后，不同搬运方式次总体所对应的沉积过程个数及其在粒度分布中所占百分比均可定量确定。

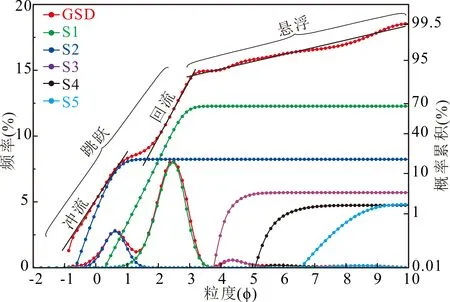
图10 粒度分布及其次总体的频率及概率累积曲线(赣江三角洲下平原分流河道沉积物样品)Fig.10 Frequency and probability cumulative curves of GSD and subpopulations (sample in the distributary channel of the Ganjiang delta lower plain)

6 结论

利用偏正态概率分布从214份鄱阳湖现代沉积物的粒度分布数据中分离得到了977个次总体，研究了次总体参数特征及沉积意义，得到以下结论和认识：

(1)次总体均值主要为0～1φ、1～2φ、2～3φ、4～5φ、6～7φ和7～8φ。均值为0～2φ的次总体分选性极好，均值为2～3φ的次总体分选性极好—好，均值为4～5φ的次总体分选性极好—较好，均值为6～8φ次总体的分选性随着均值的减小而变差。均值为4～5φ和6～8φ次总体主要为极粗偏；次总体偏度均小于0.8。均值为4～5φ和6～8φ次总体的所占百分比一般不超过30%。次总体的最大频率均不超过12%，且均值为4～5φ次总体的最大频率小于3%、均值为6～8φ次总体的最大频率小于2%。次总体的所占百分比与最大频率呈线性正相关关系。

(2)从曲流河河道到河流末端，在粒度分布中占主导的次总体粒度均值逐渐减小，最大频率大于2%的次总体个数逐渐增多。河道间洼地和湖区的沉积物粒度分布次总体占比接近，无明显的主要次总体，且细粒组分极粗偏严重。受风改造的河漫滩沉积物粒度分布频率曲线为主要为单峰，主要次总体的最大频率约10%，所占百分比可高达90%以上。在河流末端顺流方向上和河道左右两侧远离河道方向上，粒度分布的主要次总体均值逐渐较小，最终转变为次总体占比接近。

(3)江心洲沉积物的粒度分布主要由8种类型的次总体组成，其中河道砂粒度分布主要包括均值为0～1φ且最大频率小于2%、均值为2～3φ且最大频率大于6%和均值为4～5φ且最大频率小1%的3种次总体；河漫滩细粒粒度分布主要包含均值为0～1φ且最大频率2%～5%、均值为1～2φ、均值为2～3φ且最大频率小于5%、均值为4～5φ且最大频率1%～2.5%和均值为6～8φ的5种次总体。

(4)利用偏正态概率分布可以分离粒度分布中叠加的次总体，计算各个次总体的参数为沉积环境的定量化判断提供了一种新思路。结合粒度分布概率累积曲线和分离的次总体，可以定量计算不同搬运方式的所占百分比和确定对应的沉积过程个数，为沉积过程的定量化研究提供参考。