基于滑模控制的电池模拟器仿真与研究*
2022-06-07曹文章戴袁园
胡 霞,曹文章,戴袁园
(安徽理工大学 电气与信息工程学院,安徽 淮南 232000)
0 引言
电池模拟器是用来模拟电池充电、放电特性的设备,储能技术是解决可再生能源并网难题的关键技术,若使用储能电池原型进行研究,一方面采购费用高,另一方面研究时电池损坏研究成本也比较大,所以有必要使用电池模拟器来代替储能电池原型进行研究与试验。目前电池模拟器的不足之处之一为拓扑不足,在不控整流器+DC/DC 变流器的拓扑能量只能单向流动,无法双向流动,只能模拟电池的放电工况,无法模拟电池其他工况,故对可冲可放电池模拟无能为力[1-4]。本文采用电流可逆斩波电路,它是将降压斩波电路与升压斩波电路组合在一起,电流可正可负[5]可以模拟出电池充电放电过程。同时本文采用滑模变结构控制方法,这种控制策略与其他控制的不同之处在于系统的“结构”并不固定,而是可以在动态过程中根据系统当前的状态有目的地不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动[6-7]。与传统的PI 控制相比,滑模控制的鲁棒性、动态性能更好,通过仿真实验结果对比验证了滑膜控制的优越性与电池模拟器电流可正可负的可行性。
1 电池模拟器主电路拓扑结构
电池模拟器电路如图1 所示,定义V1为电网,V2为电池,D1、D2为二极管,L为电感,C为电容,r为负载电阻。通过控电容电压的方式实现电流双向流动模拟电池的充放电过程。

图1 电池模拟器拓扑结构
当电容电压高于电池电压V2时,电网V1向电池V2充电,从电路结构上看类似于Buck 电路;当设定V2的电压高于电容电压时,电池V2开始放电,从电路结构上看类似于Boost 电路,因此整个电路的电流正反向流动取决于电容电压与电池电压的大小,在工业设计上更容易实现,且整个系统为一套控制方法,解决了工业设计上硬切换的问题,真正实现了电流的正反向流动。
1.1 电池模拟器滑模设计
文献[8]提出的电池模拟器方案只能实现电流单向流动,只能单一地模拟出电池放电或者充电,无法满足测试电池的各种工况。图2 所示为本文电池模拟器滑模设计结构示意图。
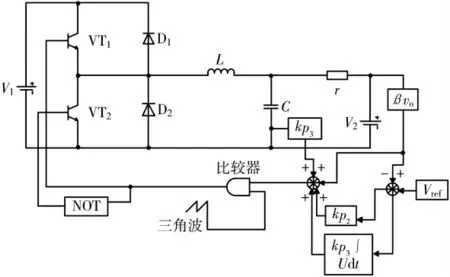
图2 电池模拟器滑模设计结构示意图
从图2 可以看出,其控制方式与电流电压双闭环控制类似,不同的是三角波信号为βv1,输出电压采集为βvo,PWM 信号会根据三角波的幅值变化而变化,系统的抗干扰能力增强、鲁棒性更好,当电容电压大于电池电压时,电网的能量流向电池,模拟电池充电过程,VT1与VT2得到的信号取反,不同时导通。当开关管VT1导通时电流经过电源正极、VT1、电感、负载、电源负极;当开关管VT1关断时,VT2导通电感续流,电流方向不变。同理电容电压小于电池电压时,电池的能量流向电网,当VT1开通时VT2关断,电池与电感的能量经过VT1、V1、V2负极;当VT2开通,VT1关断时,V2为电感L充电,电流经过负载电阻r、电感L、VT2、V2负极,模拟电池放电过程,整个电路工作在连续导电模式。
1.2 电池模拟器滑模设计算法
文献[9]中提出设计出采用滞环调制的滑模控制,其设计简单,仿真方便,但是对于实物实现较困难,同时会使滤波器的设计也很困难。文献[10]提出了的滑模控制方法只引入了电压误差状态变量,对于负载波动时无法做到调节稳定。本文采用定频滑模控制,使得其工业实现简单,因为开关管VT2信号取反VT1,所以本次设计只针对VT1。由于开关管只有通与断,因此控制率u 为1或者0,第一步构造合适的滑模面,本次设计采用比例积分微分滑模面,如式(1)所示:

选择电压误差x1与电压误差对时间的导数x2和电压误差对时间的积分x3为状态变量,得到x1、x2、x3表达式。

其中,u 代表开关状态,开关打开时u=1,开关断开时u=0。
所以得到了x1、x2、x3对时间的导数。
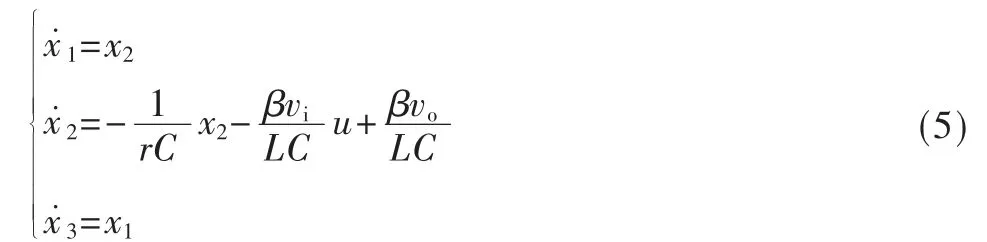
根据上文提到的3 种状态变量,所以本次滑模控制的切换函数表达式为:
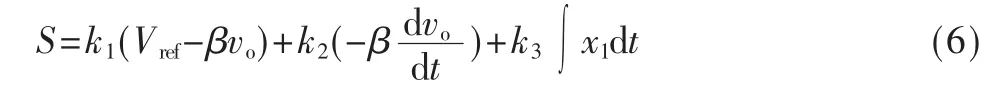
其 中,k1、k2、k3为滑模系数。对式(6)求导可得得:

将u 等效为连续值ueq,解式(7)可得:
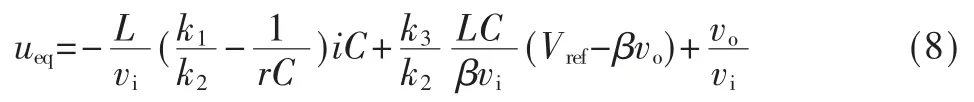



2 仿真结果与实验
本文通过MATLAB/Simulink 软件搭建了电池模拟器的滑模控制仿真和PI 控制仿真,以此来对比出滑膜控制的优势,其中两个系统的参数设置相同,误差状态变量根据式(10)取电容电流Ic、输出电压Vo,电压误差Vo-Vref,电压误差积分,为了减小电压纹波系统,仿真模型图如图3 所示。

图3 仿真模型图
模拟电池充电时,主要参数如下:仿真时间为0.02 s,直流电源V1=24 V,电感值为0.16×10-3H,电容值为500×10-6F,频率为10 kHz,负载值为20 Ω,k1=-8,k2=200,k3=100,k3调节系统平衡时间,k3越大系统达到平衡的时间越快,但是若其值过大,系统会出现紊乱现象,当选取负载为20 Ω 时,给定输出电压为10 V,电池电压V2=5 V 时,此时电网电能向电池V2充电,得到10 V 的电压波形与0.25 A 的电流波形。相比较于PI 控制,滑模控制到达平衡点的时间更短,当发生负载波动时,滑模控制的恢复时间更短,切电流电压超调量更低,仿真结果如图4 所示。

图4 电池充电仿真结果
由图4 可以看出,滑模控制下的电池模拟器到达平衡比PI 控制更快,且电压电流的超调量更低。同时,当发生负载波动时,滑模控制恢复到预定值的速度比PI控制更快,体现出滑模控制的鲁棒性和动态性能更好。
当选取负载为20 Ω 时,给定输出电压为10 V,电池电压V2=30 V 时,得到10 V 的电压波形与1.5 A 的电流波形。相比较于PI 控制,滑模控制到达平衡点的时间更短,当发生负载波动时,滑模控制的恢复时间更短,切电流电压超调量更低,仿真结果如图5 所示。

图5 电池放电仿真结果
由图5 可以看出,当模拟电池放电时,滑模控制的电池模拟器电压电流超调量比PI 控制要小,当负载发生波动时滑模控制下的系统达到平衡的速度更快,相比于PI 控制有着更好的鲁棒性与动态性能。
3 结论
本文分析了电池模拟器的整体结构,提出了新的拓扑结构,实现了单一电路电流可双向流动;同时在传统的PI 控制的基础上,提出了一种滑模控制方法,详细地阐述了该控制方案的设计思路和实现方法,提高了系统的鲁棒性和动态性能;并且在仿真软件MATLAB/Simulink 上建立模型对比验证了滑膜控制达到平衡的时间、电压电流超调量、动态性能都要优于PI 控制,具有一定实用与研究价值。
