考虑电动汽车用户满意度的微电网双层多目标优化调度
2022-06-07刘明杭梁英达
刘明杭,田 书,梁英达
(河南理工大学电气工程学院,河南省 焦作市 454000)
0 引言
随着能源的日益短缺,以及电动汽车(electric vehicle,EV)在我们日常生活中的普及应用,EV 这个规模庞大的分布式储能装置(distributed energy storage,DES),便成为了电力系统优化调度中重点的研究对象[1-3]。然而,当EV 以高渗透率接入微电网时,无序充放电行为将会给微电网带来巨大的威胁[4-7],采取高效的控制策略是解决问题的关键。
目前,国内外对于含EV 的微电网优化调度研究主要集中在减少微电网的运行成本,增加可再生能源的消纳率,减小峰谷差额等方面[8-9]。文献[10-11]通过优化EV 的充放电功率,改善负荷特性,在降低系统运行成本的同时,促进风电消纳。文献[12-13]将EV作为可调度负荷,采用分群优化的策略使得调度周期内负荷方差达到最小。文献[14]提出了基于分时电价的电动汽车多目标优化充电策略,用以解决无序电动汽车负荷导致的新高峰问题。文献[15-16]提出一种双层的调度策略,该策略对负荷峰谷差的调控能力以及可再生能源消纳水平都有了进一步提高。文献[17]建立了一种电网与换电站协调的多目标实时充放电调度系统。文献[18]则指出用户满意度对于优化调度存在一定的影响,当用户满意度低于阈值时,会导致实际的负荷曲线产生偏移。
对于用户满意度的研究,如今也有了一些成果。用户参与调度的积极性直接影响了优化调度效果,如何在保证用户满意度的情况下进行调度,如何设计用户参与市场的激励机制,是电力市场需要解决的首要问题[19-20]。文献[21]提出了一种考虑用户满意度的电动汽车分群调度策略,在优化调度时考虑用户满意度的情况。文献[22-23]建立了用户满意度模型并定量计算了综合用户满意度。文献[24]考虑风电与满意度的电动汽车智能电网充放电策略,然而以上文献都只参考了整体用户满意度,没有考虑单个EV 用户的满意度。
由于影响用户满意度的因素较多,在优化调度过程中直接考虑用户满意度的影响,会使模型变得极其复杂难以求解。因而,本文以“配电网EV 聚合商(EV aggregator,EVA)EV 用户”的模型框架,提出一种考虑用户满意度的双层多目标优化调度方案。上层通过调度中心制定各EVA 充电计划,减小负荷波动以及系统运行成本。下层考虑用户的个性化需求,增大用户综合满意度,进行2阶段优化,确定单辆EV的充电方案。将下层优化结果返回上层,进行二次优化,得到全局最优解。
1 EV 充放电与用户评价模型建立
1.1 优化模型统构
EVA 作为配网与EV 用户的中介,其作用是对EV 集群(EV cluster,EVC)进行分布式控制。系统内含有风电、光伏、EVC以及微燃机组。EVA 通过协调用户的综合满意度,同时在配电网调度中心调度计划的共同指引下对EVC 进行充电控制。每个EVA 对其所管辖的EVC进行独立的优化调度。优化调度模型简化结构如图1所示。
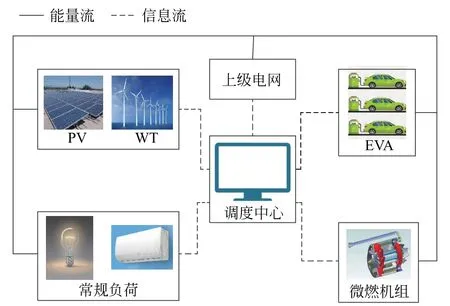
图1 双层优化调度模型结构图Fig.1 Structure diagram of double-layer optimal scheduling model
1.2 配网层模型建立
1.2.1 配网层目标函数
其目标函数是以负荷方差最小,微网系统总运行成本最低为目标,构造多目标优化模型,表达式为
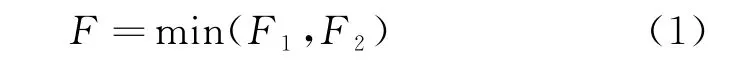
其中第一个目标为微电网净负荷方差最小,其表达式为:
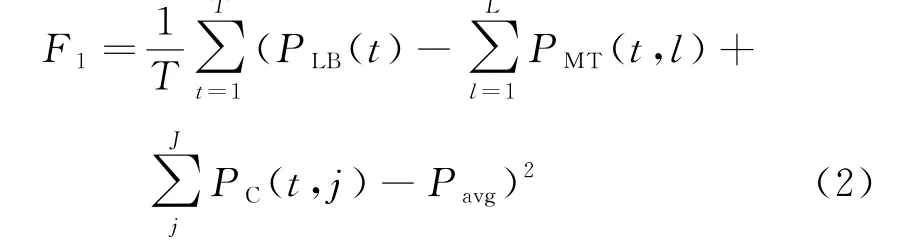
式中:PLB(t)为常规负荷;PMT(t,l)为第l 个微燃机组的t时段出力;L 为微燃机组数量;PC(t,j)为第j 个EVA 的t 时段充电功率;J 是EVA 数量;Pavg为负荷平均值。
第二个目标为微网系统总运行成本最小,其表达式为:

式中:PW(t)、PPV(t)、PG(t)分别为t 时刻风电负荷、t时刻光伏负荷、t时刻微电网向上级购电功率;CW(t)、CPV(t)分别为风电、光伏电价;CMT(t,l)为第l个微燃机组t 时刻的运行费用标准;假设微网系统电价标准、向上级购电价格标准都为C(t)。
1.2.2 配网层相关约束
(1) 微网功率平衡约束[25]
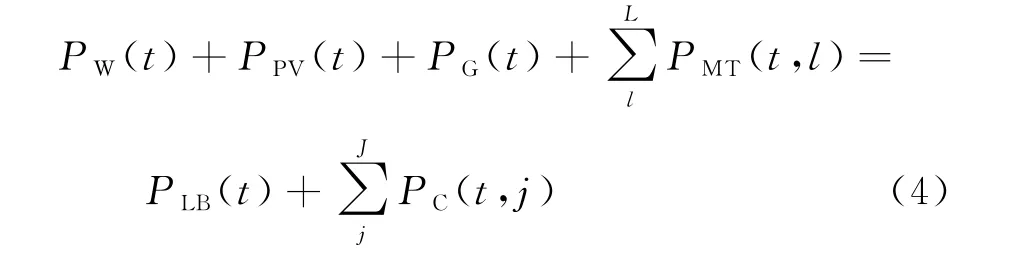
(2) 微燃机组出力约束[26]

(3) 微燃机组爬坡约束
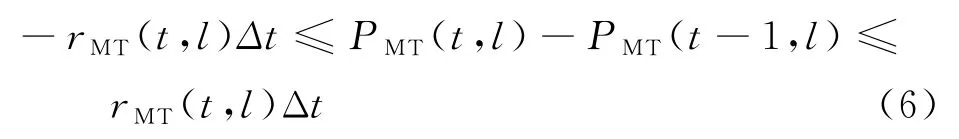
式中rMT(t,l)为第l个微燃机组t时刻爬坡速率。
(4) 系统备用容量约束条件
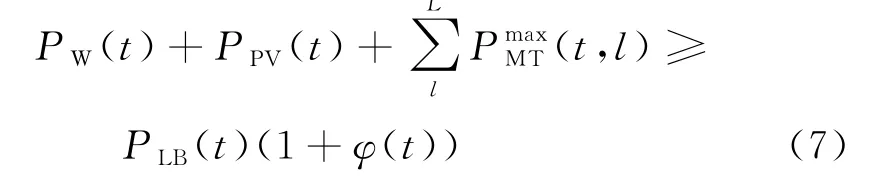
式中φ(t)为备用率。
(5) 各时段EVA 可调度功率约束
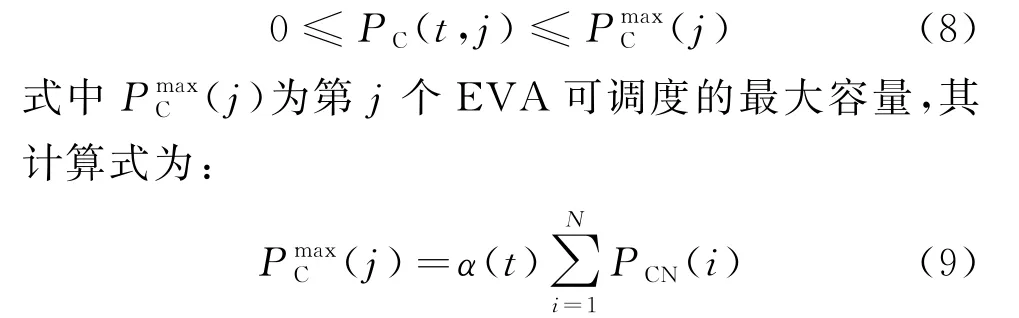
式中:PCN(i)为第i 个EV 额定充电功率;N 为EVA 可调度EV 总量;α(t)为EVA 在t 时段可调度系数,且α(t)≤1。
1.3 负荷层模型
负荷层为EVA 对可调度EV 制定充电策略。在该层采用两阶段优化方案。第一阶段考虑EV 充电需求约束,根据上层调度中心对EVA 给出的充电计划,以2层调度偏差最小为目标制定各EV 充电计划;第二阶段以用户综合满意度最高为目标,以2层之间的调度偏差不大于第一阶段的最小调度偏差为约束条件,再次确定用户充电计划。
1.3.1 第一阶段优化
第一阶段优化目标函数为
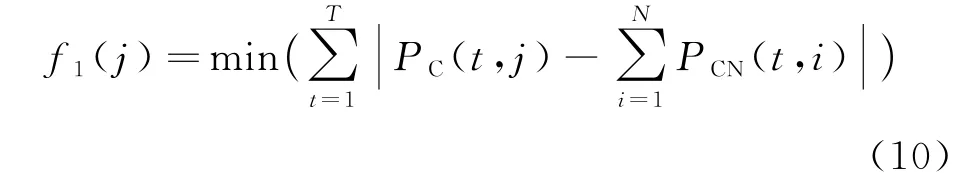
第一阶段优化相关约束包括:
(1) 车辆荷电状态(state of charging,SOC)连续性约束,即

式中:S(t,i)为车辆i在t时段的荷电状态;Sdthr(i)为车辆i储能电池电量放电时SOC阈值[27]。
(2) 离网期望SOC约束
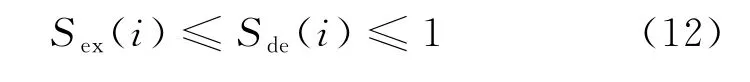
式中:Sex(i)为车辆i 离网期望SOC;Sde(i)为车辆i的离网时SOC。
(3)EV 充电功率约束
电动汽车电池的充电过程主要分为“恒流-恒压”2个阶段,恒流过程相对于整个充电过程较短,可以忽略,本文将电动车汽车的充电过程近似为恒功率特性。

式中η(t)为转化效率。
(4) 不可调度时间约束
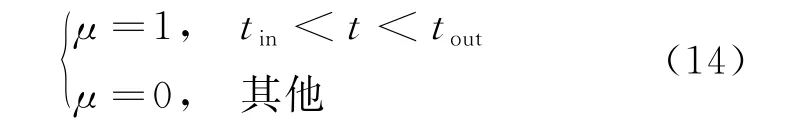
式中:μ 为充电状态,充电为1,离网为0;tin、tout分别为EA 进入停车场时刻和离开停车场时刻。
1.3.2 第二阶段优化模型
对于EVA 来说,EVA 主体参与调度的积极性直接影响了优化调度效果,因此在第二阶段以EV用户综合满意度最大为优化目标,以求在不大于上层调度计划偏差的约束下,使用户综合满意度达到最大值。满意度相关模型如下:
(1) 出行满意度
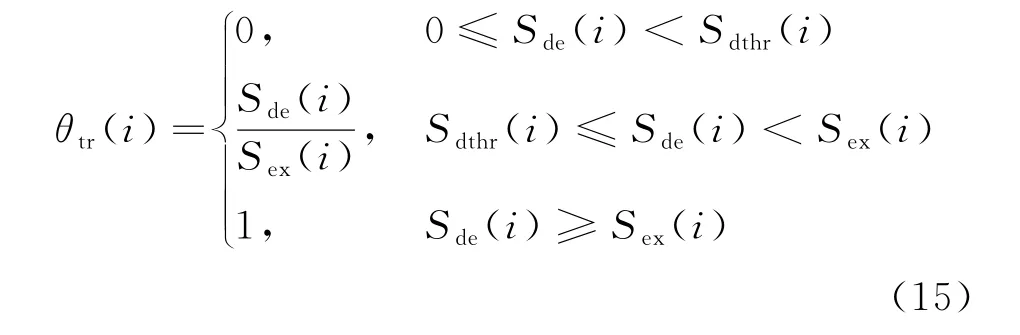
式中θtr(i)为EV 用户i的出行满意度。
(2) 费用满意度
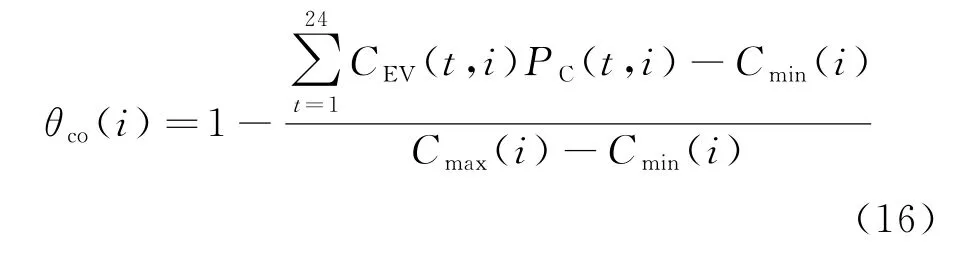
式中:θco(i)为EV 用户i 的费用满意度;CEV(t,i)为车辆i 在t 时段充电价格;Cmax(i)、Cmin(i)分别为车辆i充电的最高费用和最低费用。
(3) 综合满意度

式中θ(j)为第j 个EVA 的综合满意度。
则第二阶段优化目标函数为
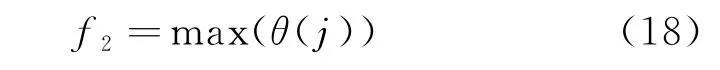
第二阶段优化相关约束包括:
(1) 调度偏差不大于第一层最小调度偏差为约束条件,即
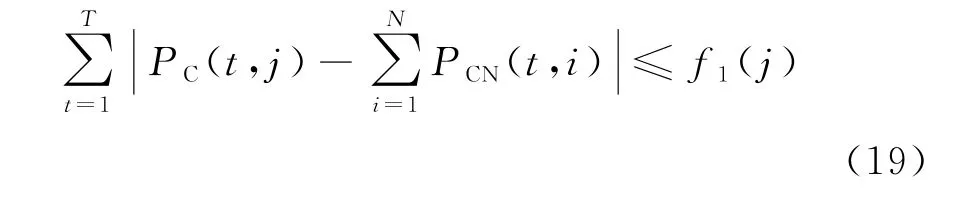
(2) 其他约束条件同式(11)—(14) 。
2 优化模型求解方法
由于上层目标函数之间难以确定合适的权重将多目标问题转化为单目标问题,因而本文采用多目标算法来求解目标函数。对于多目标函数求解问题,并不能找到唯一确定的最优解,只能求解出一个由非支配解所组成的集合,该集合被称为Pareto最优集[28]。
本文采用一种快速且带有精英保留策略的改进非劣排序多目标遗传算法(NSGA-Ⅱ)进行模型求解[29-30]。该算法采用以非支配排序为主要机制,考虑拥挤度,保证了非支配解在目标空间中分布更加均匀,提高种群的多样性,同时精英保留策略避免了优秀个体的丢失且加快了遗传算法的执行速度[31]。
得到Pareto解集后,利用模糊理论求取最优折中解[32]。将每个个体的单目标函数值进行模糊化处理,模糊化方式为

式中;Fω(w)为目标函数的第w 个前沿解;、分别为目标函数前沿解集的的最大和最小值。
将经过模糊处理的目标函数解进行加权平均,将所得解排序,得到多目标函数最优折中解,即
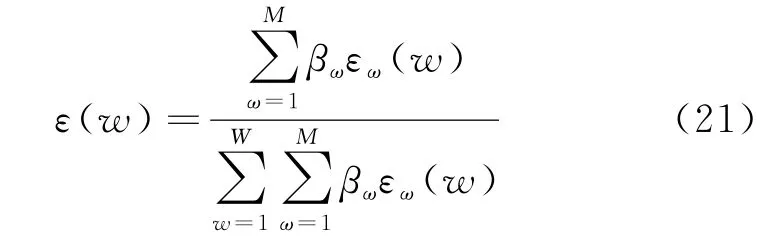
式中:βω为目标函数的权重系数;M 为优化目标个数;W 为每个目标对应的前沿解的个数。
下层是依据上层调度中心调度方案,制定EVA中EV 各时段调度计划。该问题是一个大规模含约束条件的优化求解问题。本文采用YALMIP 调用商用优化软件CPLEX[33]对模型进行求解。
3 算例分析
3.1 系统参数设置
假设系统内EV 均为同一型号,每行驶100 km耗电量为15 kW·h,充放电功率均为5 kW。本文假设EV 规模为600辆,其他参数设置为S(0,i)=0.15、Sex(i)=0.85;Sdthr(i)=0.15;η(t)=0.9;φ(t)=0.4;CW(t)=CPV(t)=0.03元/(kW·h);CMT(t)=0.085元/(kW·h);交叉概率、变异概率分别为0.9、0.1;种群规模设置为100;最大迭代次数为150。分时电价见表1,微燃机组参数见表2。

表1 配电网购电分时电价Table 1 Time-of-use electricity price of distribution network

表2 微燃机组参数Table 2 Parameters of micro gas turbine unit
3.2 仿真结果分析
为说明本文方案的有效性,选取以下3种不同场景进行测试并比较。
场景1:600辆电动汽车随机充电。
场景2:600辆电动汽车不考虑用户满意度的优化调度方案。
场景3:600辆电动汽车采用本文描述的双层多目标优化调度系统进行优化调度。
分别利用线性算法,单一NSGA-Ⅱ算法以及本文中的双层优化算法对这3种场景进行求解,其中场景3的Pareto前沿如图2所示,并进行模糊处理得到最优折中解为(298.38,37 465.09)。
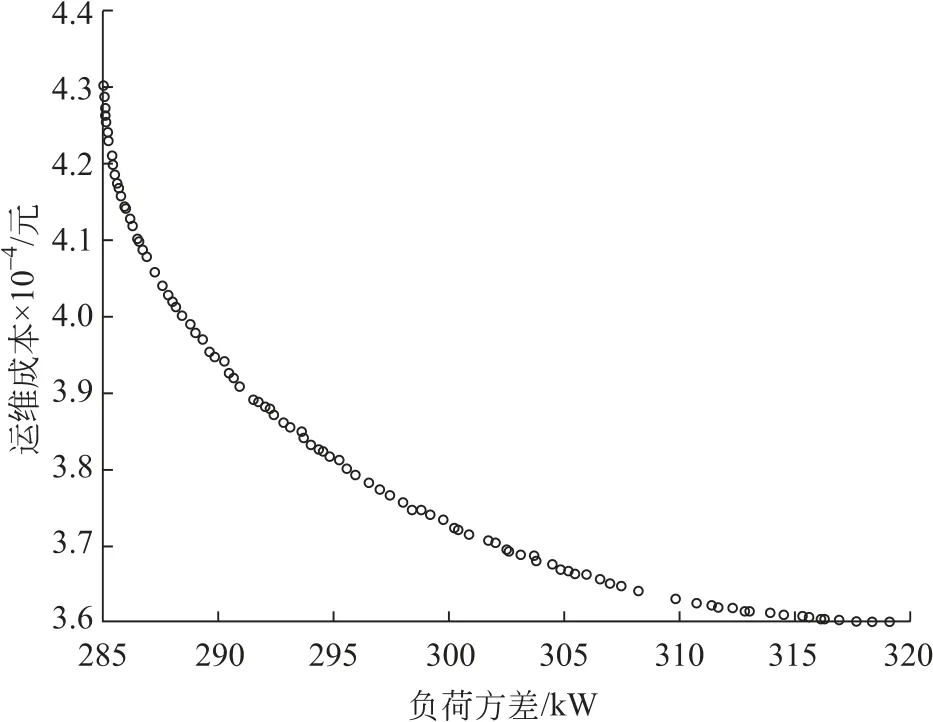
图2 双层多目标优化调度Pareto前沿Fig.2 Pareto frontier of double-layer multi-objective optimal scheduling
3种场景的EVA 充电功率计划及等效负荷功率如图3所示。等效负荷为EVA 功率与常规负荷的叠加。在EV 随即充电时,等效负荷峰谷差、日负荷方差较大,且在用电高峰期,EV 充电功率较高;不考虑用户满意度时,在01:00—05:00、21:00—24:00之间安排较大充电计划,在07:00—09:00、11:00—14:00 充电计划明显减少,等效负荷峰谷差、日负荷方差显著减小。在考虑用户满意度时,较场景2,EV 参与调度的积极性明显提高,在01:00—05:00、23:00—24:00电价较低时间段充电功率有所增加,在07:00—14:00电价较高的时间段充电计划有所减少,得益于费用满意度的提高,在15:00—17:00部分EV 用户要进行充电,充电负荷比场景2略高,以保证用户的出行满意度。
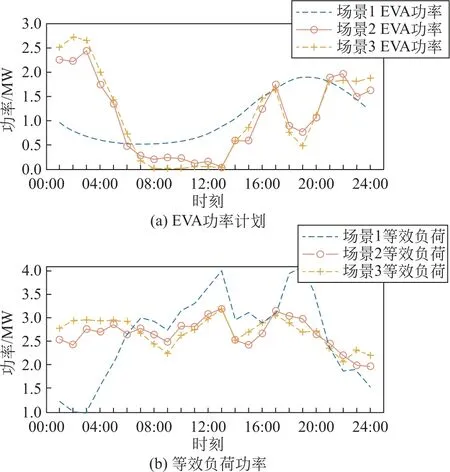
图3 不同场景下EVA充电功率计划及等效负荷功率Fig.3 EVA charging power plan and equivalent load power for three scenarios
各场景对应的各机组发电计划以及等效负荷如图4所示。由图4(a)可知:场景1情形下,当电动汽车用户随机充电时,在01:00—05:00、21:00—24:00时段等效负荷较低,在01:00—05:00时段出现弃风情况,在07:00—09:00、11:00—14:00购电成本较高的时间段,大量从上级购电,微网系统运行成本较大。
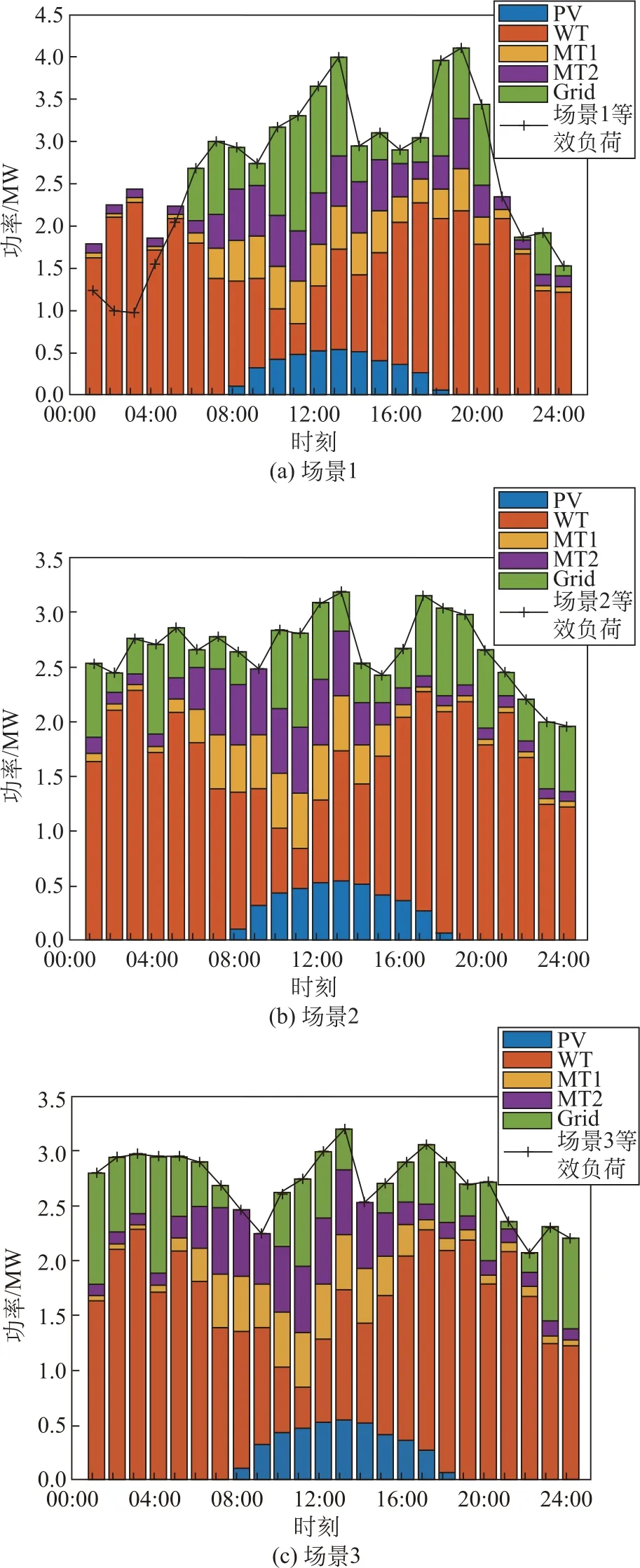
图4 不同场景下的出力分布及等效负荷Fig.4 Output loads and equivalent loads for three scenarios
由图4(b)(c)可知:不考虑用户满意度时,在01:00—05:00时段等效负荷较之场景1不再有弃风情况,在01:00—05:00、21:00—24:00电价较低时段,上级购电成本低于微燃机发电成本,将充电负荷尽可能安排在这个时段的同时,增大从上级购电量,以降低系统运行成本。而在07:00—09:00、11:00—14:00购电成本较高的时间段,上级购电量显著减少;考虑用户满意度时,在01:00—05:00、21:00—24:00电价较低时段,购电量较场景2有所提高,而在07:00—09:00、11:00—14:00电价较高的时间段,调节充电负荷,使从上级购电量再次降低,减小充电费用,提高用户费用满意度,微网系统运行成本降低。
表3为不同场景下配电网各数据指标对比。分析可知,场景1中由于在电价较高时段等效负荷较大,在电价较低时段较小,峰谷差、日负荷方差较大,且有弃风情况,总体运行费用较高;不考虑用户满意度的情况下,增加了对EVA 的调度,起到削峰填谷的作用,峰谷差、日负荷方差明显降低,运行费用也显著减小;在考虑用户满意度时,EV 用户参与调度的积极性明显增强,可调度负荷增大,使得峰谷差、日负荷方差以及运行成本再次减小,优化调度效果得到提高。
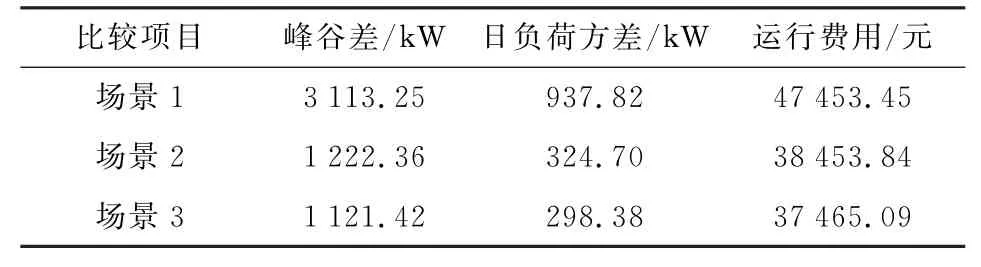
表3 各场景优化分析结果Table 3 Optimization analysis results of for three scenarios
图5为配电网在3种场景下EV 用户综合满意度对比图。由图5 可知,在无序充电的场景1 下EV 用户出行满意度较高,但费用满意度较低;在不考虑用户满意度的情况下,场景2的EV 用户的出行满意度明显下降,费用满意度得到了提高;而考虑用户满意度的场景3中,在出行满意度有了一定保障的同时,费用满意度也得到了一定的提高,其综合满意度最高。
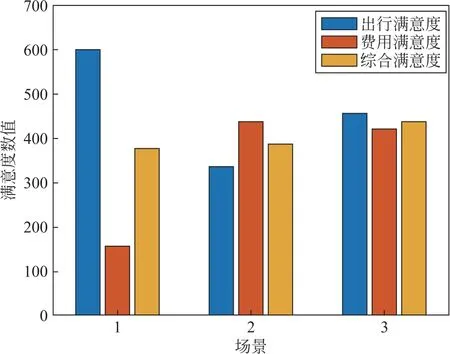
图5 EV用户综合满意度对比Fig.5 Comparison of EV users'comprehensive satisfaction
4 结论
本文针对含有高渗透率EV 的微电网系统,提出了一种考虑用户满意度的双层多目标充电优化策略。通过配电网-EV 聚合商-EV 用户的互动关系,制定兼顾配电网日负荷波动和用户满意度的充电方案,得出如下结论:
1) 通过对EV 充电以及微燃机组的协同调度,可以最大程度消纳可再生能源出力,有效减小负荷波动以及微网系统运行成本,提高微电网运行的经济性。
2) 本文提出的综合用户满意度模型,在兼顾用户出行满意度的同时,可以降低用户充电费用,提高了用户参与微电网调度的积极性,增强了优化调度的效果。
