基于虚拟激励法的大跨径连续刚构桥地震作用下力学特征分析

张俊生,张祖军

(1.中南勘察设计院集团有限公司，湖北 武汉 430000;2.长沙理工大学 土木工程学院，湖南 长沙 410014)

0 引言

近年来，连续刚构桥凭借跨径大、整体性好、受力明确等优势，在我国西南部山区大跨径桥梁建设中占据了主体地位。但西南山区属于地震频发地区，在大跨径刚构桥梁设计时必须考虑地震效应的影响[1-2]。目前已有众多学者对桥梁在地震作用下的力学响应特征进行了研究。但是目前大部分研究中对于连续刚构桥的抗震分析方法主要为反应谱法和时程分析[3]，以上2种方法对于桥梁结构抗震分析均有一定的局限性，反应谱法本质上是一种静力法，仅适用于结构线弹性工作范围，时程分析法对波形的适应度有限，仅能用于部分特定波形，因此使用以上2种方法分析结构在地震作用下的随机振动响应均有一定误差。虚拟激励法是一种高次超静定结构地震分析的方法，在特大跨径斜拉桥、悬索桥抗震分析中应用广泛[4]。本文将其引入连续刚构桥抗震分析中，探究连续刚构桥地震主梁和桥墩的力学响应特征，为大跨径连续刚构桥抗震分析提供一种新思路。

1 基于绝对位移法的虚拟激励直接求解理论

对于任一结构来说，在三维地震激励下，其振动方程可表示为式(1)[5]。

(1)

式中：S和b分别为非支撑节点和支撑节点；M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Xs为节点位移位移向量；Xb为地面强迫位移向量，其一阶和二阶导数分布为速度和加速度向量；Pb为地震力矩阵向量。

(2)

(3)

根据式(3)，求得结构支撑点位置的加速度后，即得到地震作用的实际加速度值，将式(3)代入式(1)中第1项， 并展开得到式(4)。

Kss·Xs+Ksb·us=0

(4)

移项并整理可得：

(5)

在支撑位置施加以下虚拟荷载：

-P·eiωt/ω2

(6)

式中：P表示功率谱矩阵，可由S0(w)=P*×PT分解。

联立式(5)和式(6)，可得到在虚拟激励荷载下的振动方程：

(7)

为简化计算，略去阻尼项，结构在虚拟激励荷载下的动力方程可变为：

(8)

式(8)为结构在随机荷载作用下的简谐振动方程，通过进行谐响应求解，可获得结构功率谱矩阵，见式(9)，根据功率谱矩阵，可快速求解各阶谱矩阵，结合有限元分析可方便地求解内力响应均值。

(9)

2 有限元建模和地震模型参数选取

2.1 工程概况

以某大跨径连续刚构桥为研究对象，该桥桥跨组合为(65+120+65)m，梁截面形式为单箱单室截面，主梁混凝土材料标号为C50，桥梁单幅桥面全宽为12.125 m。根部梁高为9 m，跨中截面梁高3.5 m，变截面段箱梁高度按1.8次抛物线变化。整体结构为三向预应力结构。下部结构为矩形墩，混凝土标号C40。桥址地震烈度为Ⅶ度，峰值加速度为0.05g，反应谱特征周期0.35 s。桥型布置图和截面图见图1、图2。

2.2 有限元建模及参数选取

在ANSYS中直接实现虚拟激励荷载的模拟是极其困难的，传统方法是通过将绝对位移分解为等

图1 桥型布置示意图(单位：cm)Figure 1 Schematic diagram of bridge layout (Unit:cm)

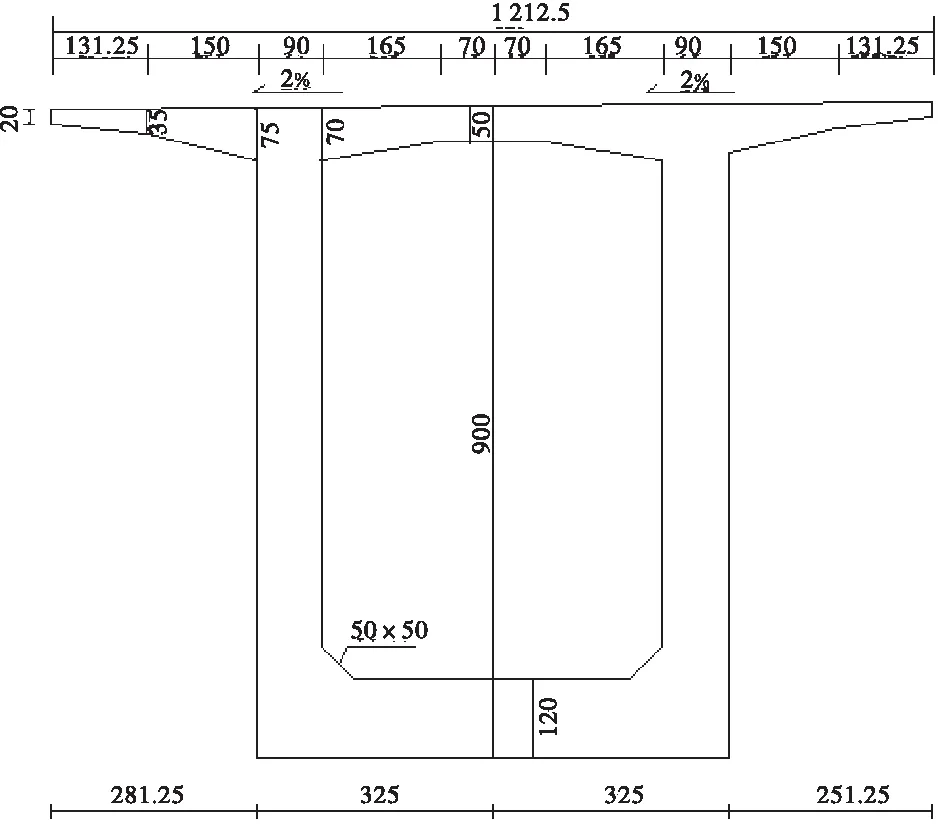
(a) 支点截面

(b) 跨中截面

效静力位移项和相对动力位移项，一般均需确定静力影响矩阵，再根据影响矩阵确定静力项和动力项的虚拟激励荷载。当结构自由度较多时，静力影响矩阵会非常庞大，求解十分困难。而基于“大质量法”，通过在支撑位置施加极大质量块，在大质量块上施加虚拟激励荷载，将地震加速度求解等效为求解结构在支撑位置的加速度。该法可极大提高虚拟激励法在有限元分析中的计算效率[6-8]。

使用APDL语言建立该桥ANSYS有限元模型，其中，主梁和主墩使用梁单元Beam188模拟，为简化计算，不考虑桩-土作用的影响，主墩底部使用固定约束条件，两侧桥台位置约束竖向位移，墩梁之间使用面固结约束。在各约束建立Mass21质量单元，以便于施加大质量块(一般取结构质量的106～109倍，本文拟取108)。有限元模型见图3。

图3 有限元模型示意图Figure 3 Schematic diagram of finite element model

使用Block Lanczos法求解桥梁结构自振频率[9]，表1和图4给出了该桥部分阶次的振动频率和振型计算结果。

从振动频率分析结果可以看出，该桥模态分布呈跳跃式，临近阶次模态相互干扰的可能性较小，模态成分相对于斜拉桥而言较为简单，振型没有出现明显的空间叠加效应和耦合现象。根据设计地勘资料，按Ⅶ度烈度区、场地类型为Ⅱ类进行分析。

表1 桥梁部分阶次振动频率Table 1 Part of the order vibration frequency of the bridge 阶次频率/Hz阶次频率/Hz10.659 6207.326 220.960 83010.135 831.211 34013.069 841.341 15015.326 552.462 76017.782 462.463 47019.433 573.074 78021.214 383.824 59023.125 294.305 110025.076 9105.114 7

选用Clough-Penzien谱模型作为地震功率谱输入模型，该模型基于Kanai-Tajimi模型改进而来，克服了K-T模型在w=0时出现奇异的缺点，消除了其在低频状态下夸大地震地面运动的问题[10]，其表达式可表述为式(10)。

(10)

式中：S0为白谱强度，是一个频率无关的量；ξg为

(a)主梁纵飘

(b)主梁一阶正对称横弯

(c)主梁一阶反对称横弯

(d)主梁一阶正对称竖弯

(e)主梁一阶反对称竖弯

f)主梁二阶正对称横弯

土层阻尼比；ωg为卓越角频率；ωf、ξf为低通滤波项参数。

根据地勘资料结合相关研究成果，对各参数取值如下：ωg=13.96 rad/s；ξg=ξf=0.8；ωf=2.792 rad/s；S0=7.123 cm2/s3。在Matlab中求解功率谱矩阵后，将其输入有限元软件中即可求得随机地震作用下结构内力响应结果。

3 主梁计算结果

将各取值参数输入至ANSYS模型中，根据“大质量法”模拟虚拟激励荷载，在ANSYS中计算获取各响应的功率谱，而后根据随机振动理论得到结构力学响应结果。本文拟考虑以下工况进行对比：工况1：纵向地震波激励；工况2：横向地震波激励；工况3：纵向+横向地震波激励；工况4：纵向+竖向地震波激励；工况5：三向激励。

3.1 一维地震激励下主梁力学特征

图5、图6和表2给出了主梁在一维多点激励下(工况1、工况2)部分关键截面弯矩、剪力和位移均方根响应结果，由计算结果可知：①在纵向地震波激励下，主梁纵向弯矩均方根最大为6 884.2 kN·m，对竖向剪力影响较小，最大剪力均方根为657.58 kN；②在横向地震波激励下，弯矩值普遍较大，横向最大弯矩值达32 500.4 kN·m，同时横向地震波会使结构产生纵桥向弯矩，均方根值与工况1中的弯矩值相当，横向激励对剪力的影响与工况1 大体相当；③主梁在2种工况下的竖向位移均方根结果基本一致，没有明显差别，在横向激励下最大横向位移均方根为6.87 mm。由此可知，在一维地震激励下，横向激励主梁内力响应远大于纵向激励，同时，横向激励会使得结构产生纵向弯矩，说明结构在地震作用下的内力响应呈现出耦合现象。

(a) 纵向

(b) 竖向

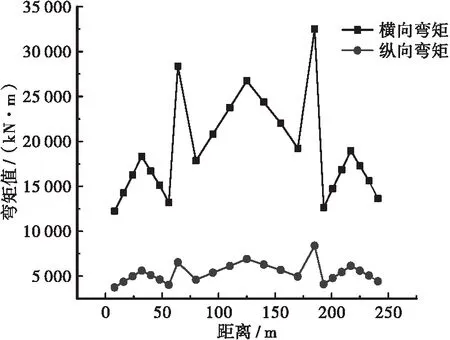
(a) 横向与纵向

(b) 横向

表2 工况1、工况2主梁部分关键截面位移均方根对比Table 2 Comparison of root mean square of displacement of key sections of main girder in working condition 1、condition 2 mm截面工况1工况2竖向位移竖向位移横向位移左边跨L/416.8516.392.35左边跨L/228.5227.743.42左边跨3L/413.2412.884.62左侧墩顶2.112.253.95中跨L/431.5433.624.13中跨L/242.8745.696.87中跨3L/433.4736.824.26右侧墩顶3.413.753.27右边跨L/418.8218.234.43右边跨L/230.0429.093.84右边跨3L/416.7316.202.67

3.2 二维地震激励下主梁力学特征

图7给出了工况3、工况4作用下主梁部分关键截面纵横向弯矩响应均方根结果，计算结果表明：在纵向+横向二维地震激励下，主梁纵向弯矩与纵向一维激励影响效应保持一致，横向弯矩与一维横向激励基本一致，二维激励下弯矩值略高；在纵向+竖向二维地震激励下，结构纵向弯矩均方根值较纵向一维激励小，降幅在6%～10%之间，分析原因为在该工况下激发了主梁反对称振型，导致弯矩效应减小。

表3给出了工况3、工况4作用下主梁关键截面位移均方根响应结果，由计算结果可知：工况3相对于横向一维激励(工况2)竖向，及横向位移略有增大，但影响规律基本一致；工况4竖向位移相对于纵向一维激励(工况1)略有减小。位移均方根响应结果与主梁弯矩响应结果规律大致相同，两者起到了相互验证的效果。

3.3 三向地震作用下主梁力学特征

图8给出了工况5作用下主梁部分关键截面纵横向弯矩响应均方根结果，计算结果表明：在三向地震激励下，主梁纵向、横向弯矩均方根结果均小于纵向+横向二维激励下主梁弯矩效应，其原因仍为竖向激励下反对称振型被激发造成的，其主梁竖向、横向位移也相比纵向+横向二维激励时略小，原因上同，在此不再赘述。

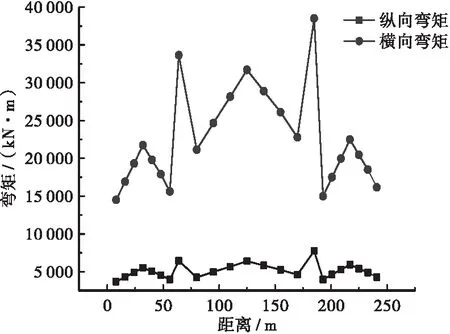
(a) 纵向与横向

(b) 纵向

表3 工况3、工况4主梁部分关键截面位移均方根对比Table 3 Comparison of root mean square of displacement of key sections of main girder in working condition 3、condition 4 mm 截面工况3工况4竖向位移横向位移竖向位移截面工况3工况4竖向位移横向位移竖向位移左边跨L/418.732.5216.42中跨3L/438.984.7930.95左边跨L/231.703.6727.78右侧墩顶3.973.673.23左边跨3L/414.724.9612.90右边跨L/419.305.0917.82左侧墩顶2.574.241.95右边跨L/230.804.4128.44中跨L/438.424.4429.17右边跨3L/417.153.0715.84中跨L/252.217.7239.64

图8 工况5主梁弯矩均方根响应图Figure 8 Root mean square response diagram of main beam bending moment of working condition 5

4 主墩计算结果

以左侧桥墩为例，对比分析5种工况下桥墩受力及变形规律，为节约篇幅，选取墩底、墩身1/2处，墩底3个关键截面，分别提取各工况下弯矩均方根和位移均方根计算结果。

表4给出了各工况下桥墩关键截面纵向及横向弯矩均方根响应结果，计算结果表明：①对于一维激励，桥墩弯矩值由该方向激励力控制，如在纵向激励下，桥墩纵向弯矩值最大，在横向激励下，桥墩横向弯矩最大；②纵向+横向二维激励下，桥墩纵、横向向弯矩与纵向、横向一维激励时对应弯矩值大致相同，其值略高；③对于二维或三维激励，竖向激励将激发结构反对称振型，使得桥墩弯矩有较小的趋势。

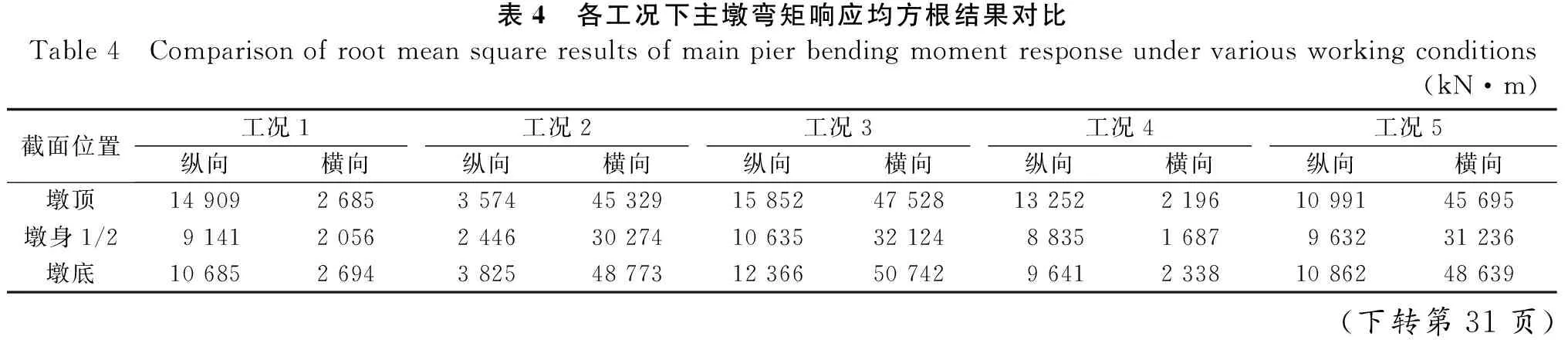
表4 各工况下主墩弯矩响应均方根结果对比Table 4 Comparison of root mean square results of main pier bending moment response under various working conditions (kN·m)截面位置工况1工况2工况3工况4工况5纵向横向纵向横向纵向横向纵向横向纵向横向墩顶14 9092 6853 57445 32915 85247 52813 2522 19610 99145 695墩身1/29 1412 0562 44630 27410 63532 1248 8351 6879 63231 236墩底10 6852 6943 82548 77312 36650 7429 6412 33810 86248 639

表5给出了各工况下桥墩墩顶截面位置纵向及横向位移均方根响应结果，计算结果表明，结构的横向位移主要由横向激励控制，竖向激励下，反对称振型的激发会降低桥墩位移值，同时，由工况1～工况2对比结果，横向激励对纵向位移的影响

表5 各工况下主墩位移响应均方根结果对比Table 5 Comparison of root-mean-square results of main pier displacement response under various working condi-tions mm工况纵向横向工况121.68.5工况213.436.2工况323.438.3工况417.87.6工况525.627.4

要大于纵向激励对横向位移的影响。其他变化规律与主梁变化规律大致相同，不作赘述。

5 结论

以某刚构桥为研究对象，基于随机振动理论，将虚拟激励法应用至大跨径连续刚构桥梁的抗震分析中，对比分析了一维、二维、三维共5种工况激励下主梁和桥墩力学响应特征，可得到以下结论：

a.一维地震激励，纵向激励荷载控制纵向弯矩，横向激励荷载控制横向弯矩；二维地震激励下，纵向+横向激励工况中纵向、横向弯矩与一维纵向、横向激励下弯矩响应规律大体相同，数值略有增大。

b.二维纵向+竖向激励下，结构弯矩响应小于一维纵向激励，这是由于竖向激励荷载激发了结构反对称振型，三向激励的主梁弯矩规律与二维纵向+竖向激励一致，原因相同。

c.主梁桥墩弯矩和位移变化规律跟主梁类似，其中横向激励下桥墩位移响应较纵向激励大，在抗震设计时应加强墩柱横向刚度。