海洋柔性管道螺旋结构弯曲行为的有限元分析

郭泽鹏， 汤明刚， 李生鹏， 郑文慧

(中国船舶科学研究中心，江苏 无锡 214082)

海洋柔性管道作为海上传输油气的重要装备[1]，其特点是由多层独立的复合结构组成，对于深水作业中易出现的受力弯曲、径向拉伸、管道内外压强等载荷工况均具备良好的适应性。典型的海洋柔性管道由金属层和复合物层构成[2]，其中抗拉铠装层是由多股矩形钢丝螺旋缠绕形成的一层保护结构，主要用于承担海洋柔性管道的轴向拉力载荷，避免管道在弯曲状态下发生结构断裂破坏。该类螺旋结构在弯曲载荷作用下的力学行为是管道设计时需考虑的关键因素之一，但由于管道的多层复合结构形式导致结构间存在大量的接触摩擦，该类螺旋结构的滑移形态和应力响应尚未有明确的结论，为管道的设计带来了困难。

Feret等[3]基于最短滑移路径假设认为管道弯曲时钢丝仅发生副曲率的变化，推导出了螺旋钢丝的应力响应并计算得到滑移量。Witz等[4]认为螺旋钢丝仅沿管道轴线方向发生滑移，推导得到了钢丝轴向应力的分布，并依此对钢丝滑移形态进行了推测。Costello[5]基于Love 螺旋曲杆理论，从计算中得到在独立弹簧模型下螺旋钢丝的应力状态。上述理论方法均基于一定假设条件，无法考虑有内部圆柱体的摩擦与支撑作用下的结构行为，因此国内外学者将有限元分析方法引入了螺旋结构弯曲行为研究。汤明刚[6]针对抗拉铠装层建立了管道结构有限元模型，得到了在弯曲作用下的结构应力响应分布，但没有进行层间滑移形态的研究。李英等[7]基于ABAQUS建立了考虑通用接触的有限元模型，得到了不同摩擦系数和螺旋角对层间滑移的影响，但没有对螺旋钢丝滑移路径进行研究。左亚东[8]采用体-壳单元模拟了管道结构层间相互作用，对弯曲过程中螺旋钢丝的结构应力响应进行了有限元分析，有效降低了计算成本但无法模拟层间的真实作用情况。综上论述，探究螺旋缠绕圆柱弯曲下的行为机理，特别是考虑摩擦、滑移等的影响，是非常必要的。

本文基于的相关理论与技术研究，针对深水柔性管道抗拉铠装层中典型的螺旋钢丝结构，建立了能够准确模拟层间接触、滑移、摩擦等复杂非线性作用的有限元分析模型，并对海洋柔性管道螺旋结构弯曲行为进行了定量分析。

1 有限元计算模型

1.1 抗拉铠装层结构

海洋柔性管道主要由骨架层、内衬套、抗压铠装层、耐磨层、抗拉铠装层、外包覆层等多层非粘结复合结构组成[9]，其结构形式如图1所示。

图1 深水动态柔性管道典型结构示意

本文以一型深水柔性管道的抗拉铠装层为例，截取一段4 m长的管道试件作为研究对象进行计算分析，试件主要参数如表1所示。

表1 抗拉铠装层结构参数

1.2 有限元建模

开展管道全结构模型的非线性计算将消耗大量计算资源，为了合理分析管道结构在受力弯曲状态下抗拉铠装层的相对滑移形态，首先将目标结构有限元模型作如下简化与要求：

1)将抗拉铠装层以内的多层复合结构用单一正交各向异性的圆柱层替代，使之具有轴向抗拉刚度大、弯曲刚度小的力学特性，称之为内护套层；

2)考虑到抗拉铠装钢丝每根钢丝的弯曲变形是类似的，因此保留单根钢丝与内护套层的典型装配结构，并通过对钢丝在一个完整螺旋周期下的计算分析结果确定螺旋缠绕铠装层的滑移形态；

3)由于在纯弯曲作用下，抗拉铠装层与其外层结构间的接触压力较小，摩擦行为认为忽略不计，故有限元建模不考虑抗拉铠装层以外的结构。

4)根据圣维南原理[10]，在管道结构有限元模型两端施加等效作用边界条件时，远离边界的区域可以反映结构在真实作业情况下的力学响应，故保证管道试件有限元模型的长度应满足至少3个螺旋周期长度，以消除端部效应的影响。

1.2.1 单元选取与网格划分

管道试件结构采用二阶实体单元进行网格划分。为准确描述螺旋钢丝在外载荷作用下的层间滑移与应力分布情况，并减小有限元计算成本，对不同网格密度下的计算结果进行收敛性分析，螺旋钢丝相对滑移和应力响应结果如图2～3所示。

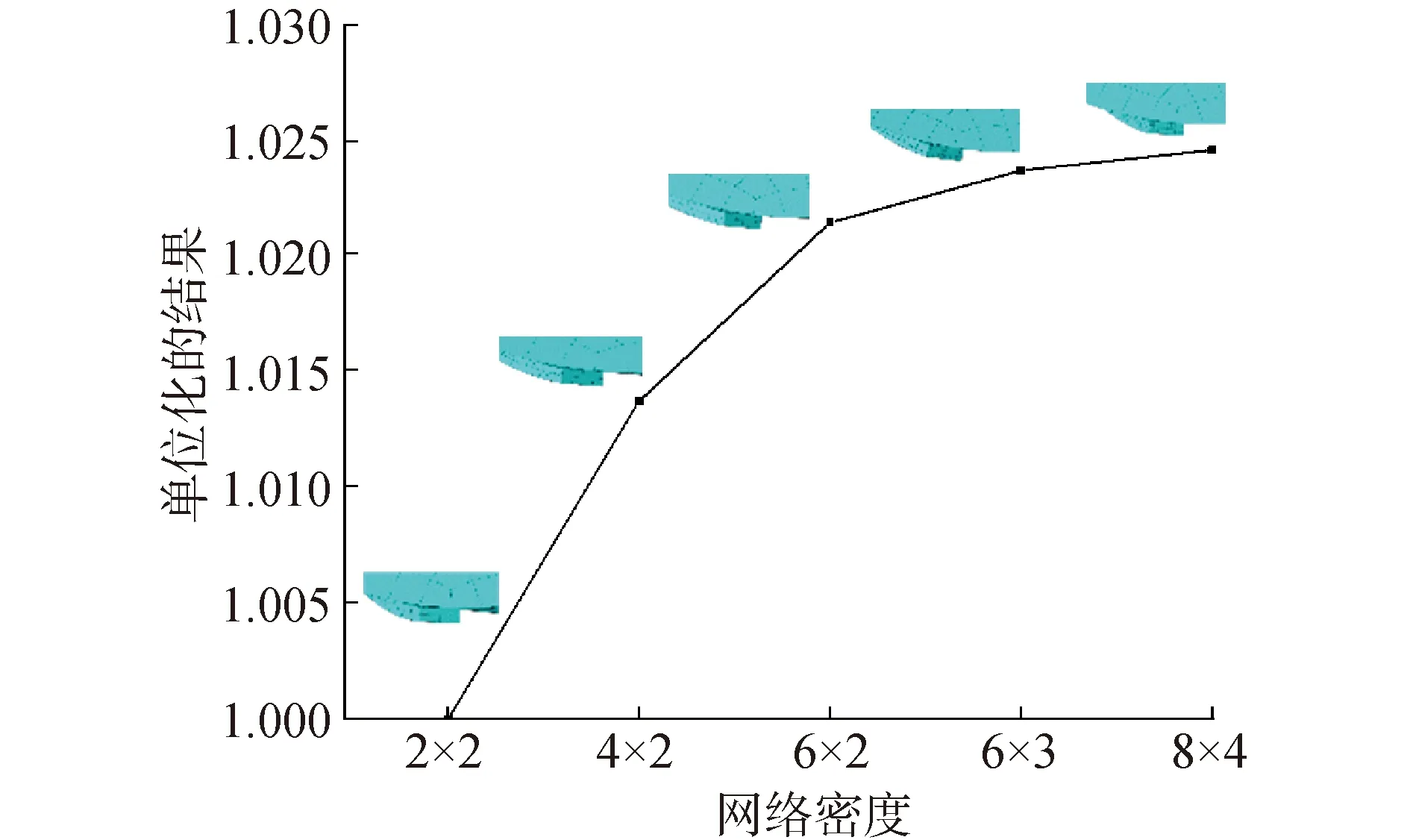
图2 层间相对滑移结果的收敛性

图3 钢丝应力结果的收敛性

根据上述计算分析可见，在网格密度6×3情况下模型计算结果即具有较好的收敛性。综合考虑计算精度与资源成本，本文计算中螺旋钢丝采用6×3网格密度进行网格划分。根据Abaqus的主-从接触算法，在有限元计算中需要限制从面节点侵入主面，故控制内护套单元网格大于螺旋钢丝单元网格。

基于柔性管道试件参数，建立单螺旋钢丝缠绕圆柱结构装配模型如图4所示。

图4 结构三维有限元模型

1.2.2 约束及加载条件

在管道模型的左右端面建立刚性约束截面：在圆柱中心位置分别建立参考点RP1、RP2，并使内护套及螺旋钢丝端面与对应端面参考点间通过MPC连接，并设置六自由度刚性约束。

在建立的2个刚性端面控制点上分别施加大小相等、方向相反的转角约束，模拟管道试件受力产生的弯曲变形。为实现管道端面转角加载，同时防止计算中模型出现刚体运动，对两端刚性端面控制点进行三自由度位移进行约束，并释放一端的轴向位移约束。

1.2.3 接触面设置

螺旋钢丝与内护套结构在初始几何上保持贴合状态，当发生弯曲时，管道的弯曲行为会受到钢丝与内护套之间接触的影响。将接触模型设置为面-面接触，并将内护套表面设为主面，螺旋钢丝表面设为从面。其中，法向接触属性设为硬接触，避免接触面之间出现相互穿透；切向接触属性分为有摩擦和无摩擦2种情况，在有摩擦情况下采用库伦摩擦模型，摩擦系数取0.1。同时考虑管道模型在弯曲过程中，螺旋钢丝可能会出现较大滑移，因此接触面采用有限滑移接触属性。

2 层间滑移分析方法

2.1 参考点选取

为描述管道受力弯曲状态下层间的相对摩擦，采用空间向量分析方法定量分析管道试件的层间相对滑移。具体来讲，分别选取在螺旋钢丝和内护套层上的参考点并使之一一对应，通过计算每组参考点在管道试件受力变形过程中的相对位移即可反映出局部结构相对滑移情况如图5所示。为反应螺旋钢丝结构整体的滑移形态，需满足测量分析范围覆盖一个螺旋周期，在管道试件模型中间段区域选定一个螺旋周期，在螺旋周期内均匀地选取参考点，每个参考点对应当前螺旋位置处内护套外表面和螺旋钢丝参考点组，通过计算每组参考点在管道模型受力弯曲过程中的相对坐标位置变化矢量，即可分析得到不同位置处螺旋钢丝相对于内护套的滑动趋势，从而得到测试区域内螺旋钢丝整体的滑移形态。

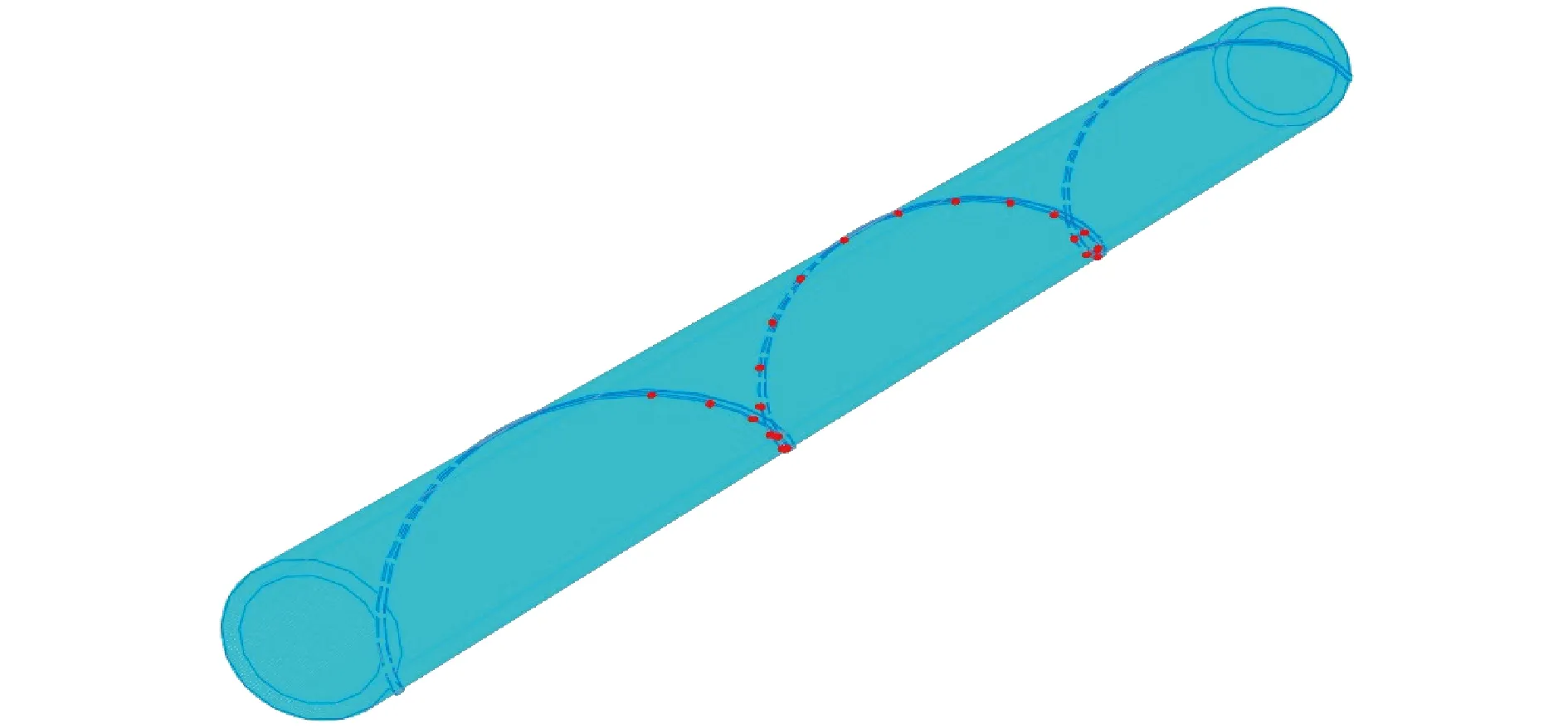
图5 相对滑移参考点位置示意

由于螺旋钢丝与内护套互为独立结构，在管道试件的实物加工以及有限元模型装配中均会存在一定间隙，为保证相对滑移计算的精确度，每组一一对应的参考点应尽量靠近，以减小结构不同位置因形变程度差异而产生的计算误差。因此，为保证每组对应的参考点间距最小，在螺旋钢丝有限元模型上选取单元节点作为参考基准点，向内护套表面作投影，得到的在内护套表面上的投影点即为距离基准点最近的参考点，并根据投影点调整内护套单元网格，参考点选取方案如图6所示。

图6 相对滑移参考点选取方法

为描述层间相对滑移形态，需对参考点的相对滑移量和滑移方向2个参数进行分析。

2.2 相对滑移量计算方法

为方便描述层间相对滑移分析方案，进行定义如下：A0-N0为分别在螺旋钢丝和内护套表面上的一组滑移参考点，A1为螺旋钢丝上与A0相邻的单元节点，N1为由A1向内护套表面的投影点。如图7所示。

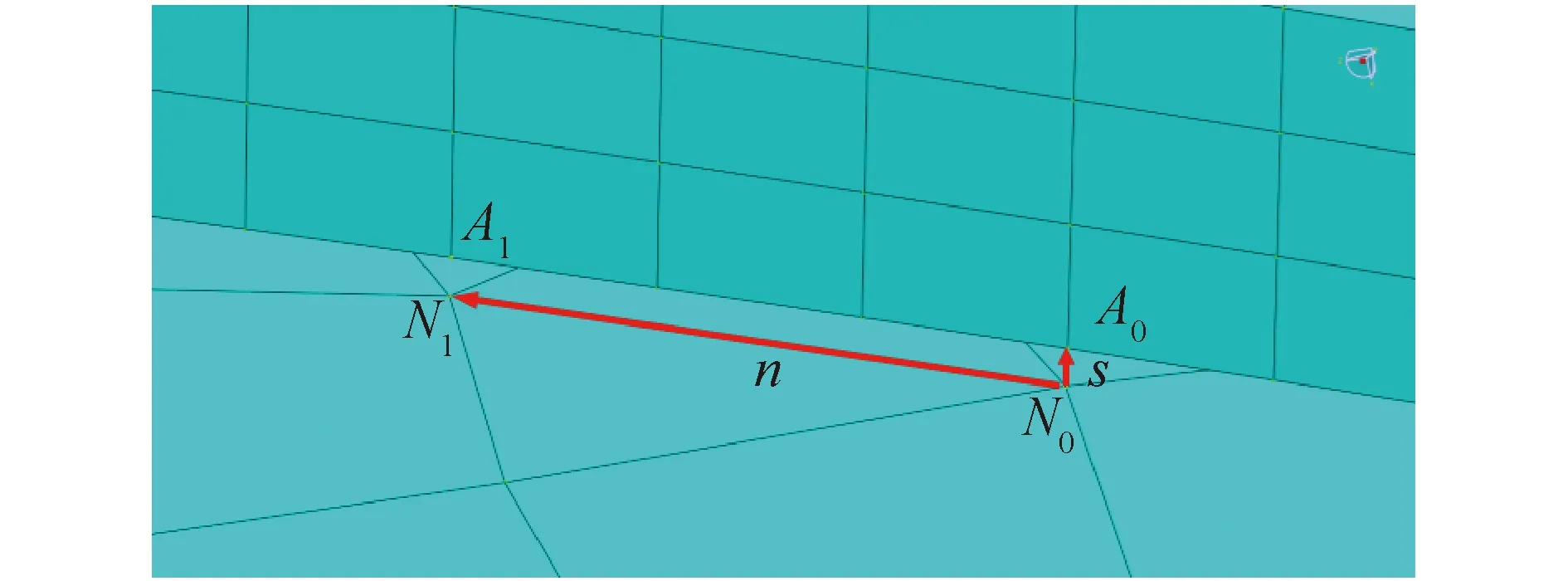
图7 相对滑移参考向量定义

对于相对滑移量，通过计算得到每对参考点组在管道受力弯曲变形前后的相对位移矢量s(x1,y1,z1)的模即可得到，即：

s=ΔN0-ΔA0

式中：ΔN0为参考点N0在结构形变前后的坐标变化值；ΔA0为参考点A0在结构形变前后的坐标变化值。

2.3 相对滑移方向计算方法

在螺旋钢丝与内护套层之间的间隙为一个小量的前提下，则可认为相对位移矢量s与2个结构层上参考点周围局部区域内的平面都相互平行。因此，为描述管道弯曲过程中的螺旋钢丝的滑移方向，需在内护套结构表面建立基准矢量作为参照。在参考点A0螺旋钢丝结构局部延伸方向上的单元网格节点处选取一点A1，表示螺旋钢丝结构局部区域延伸方向，由A1向内护套外表面做投影取得参考点N1，并调整内护套单元网格，则可得到内护套外表面在管道受力弯曲变形后的空间矢量N0-N1，记作n(x2,y2,z2)，则矢量的夹角可表示为：

计算过程中，认为管道试件在整体受力弯曲的过程中，内护套外表面发生的局部结构形变可以忽略不计，且有层间相对位移矢量s(x1,y1,z1)与n(x2,y2,z2)所在平面相互平行，则夹角θ可正确地反映出在参考点处螺旋钢丝的相对滑移方向。

3 结果分析

3.1 层间滑移形态分析

基于建立的管道结构有限元模型，计算得到在不同弯曲程度下的螺旋钢丝相对滑移量如图8所示。

图8 不同弯曲半径下相对滑移量曲线

从上述计算结果可以看出，螺旋钢丝相对内护套表面的滑移量呈周期性变化规律。螺旋钢丝相对滑移量的峰值出现在相位角φ=π/2，3π/2附近，而谷值出现在相位角φ=π，2π附近。处于螺旋钢丝与内护套在管道弯曲方向的底部位置的φ=π处发生的滑移量相对更小，这说明该处产生了较大的摩擦作用，在局部区域趋于相对约束状态。结合接触面压应力分布情况，当管道整体受力向下弯曲时，接触面压力主要出现在底部区域，这也验证了层间摩擦主要集中在管道弯曲方向的端部位置区域。

根据螺旋钢丝的相对滑移量随管道弯曲程度的变化情况可以发现，螺旋钢丝的滑动现象首先发生在φ=π/2，3π/2附近，而后向其两侧发生扩展，使螺旋钢丝整体发生滑动。

不同弯曲程度下的螺旋钢丝相对滑移方向如图9所示。

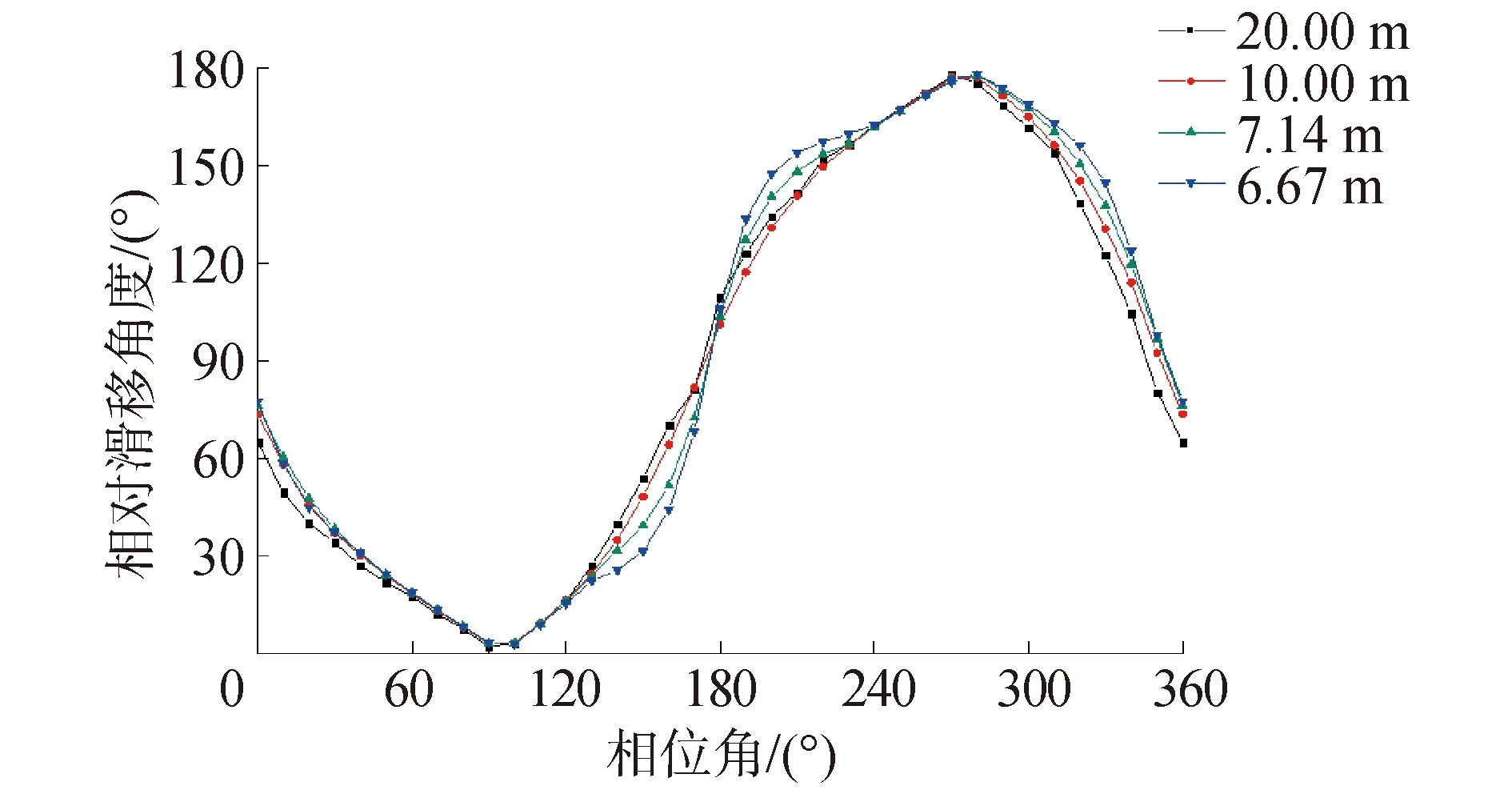
图9 不同弯曲半径下相对滑移方向曲线

从螺旋钢丝相对滑移方向计算结果可以看出，螺旋钢丝在φ=π/2,3π/2附近的相对滑移方向与螺旋结构走向基本一致，且在相邻半周期内的滑移方向相反；在φ=π,2π，即管道整体弯曲方向的端部位置附近，螺旋钢丝滑移方向呈现由正到反的快速过渡变化，局部螺旋结构走向近似于90°，尤其是在φ=π附近，随着管道弯曲程度的增大，相对滑移方向由正到反的过渡变化加快，这也说明了在管道弯曲方向的端部位置摩擦力对结构造成了较强的约束作用。

结合螺旋钢丝的相对滑移量及相对滑移方向计算结果，可以推测螺旋钢丝在管道受力弯曲状态下处于“拉伸”和“压缩”的状态，螺旋钢丝的滑移形态如图10所示。

图10 纯弯状态下螺旋钢丝滑移形态(虚线为钢丝滑移后形态)

3.2 螺旋钢丝应力响应

管道弯曲状态下，抗拉铠装钢丝的矩形截面角点处将产生局部高应力，是影响管道MBR及疲劳强度设计的关键因素。因此，本文在分析螺旋钢丝在管道整体受力弯曲状态下的力学特性时，提取一个螺旋周期内如图11所示的4个螺旋钢丝角点的应力状态作为分析目标。

图11 螺旋钢丝结构应力参考点

应力响应有限元计算结果如图12所示，其中散点图为带摩擦计算结果，实线图为无摩擦有限元计算结果。

图12 纯弯曲作用下螺旋钢丝应力结果

从螺旋钢丝角点应力计算结果可以发现，螺旋钢丝角点处应力的幅值相同且呈周期性变化趋势，最大值均出现在φ=0,2π附近、最小值出现在φ=π附近。其中，1号、4号角点和2号、3号应力值及相位分别保持一致，2组应力结果存在一定的相位差。

通过有摩擦与无摩擦2种情况计算结果对比可以发现，抗拉铠装钢丝结构的角点应力分布情况一致，并且在层间摩擦作用下的应力响应存在一定滞后，这是由于内护套对螺旋钢丝的摩擦约束作用而产生的。

为研究管道受力弯曲过程中圆柱体对螺旋钢丝法相约束作用的影响，开展仅对去除内护套结构后的单根螺旋钢丝结构在弯曲作用下的应力分布情况数值计算。作为对比验证，基于弹性力学原理进行了理论计算，将螺旋钢丝视为一根能够自由弯曲的弹簧[6]，对其在弯曲状态下的结构应力进行分析。钢丝的应力结果对比情况如图13所示，其中散点图为有限元计算结果，实线图为理论计算结果。

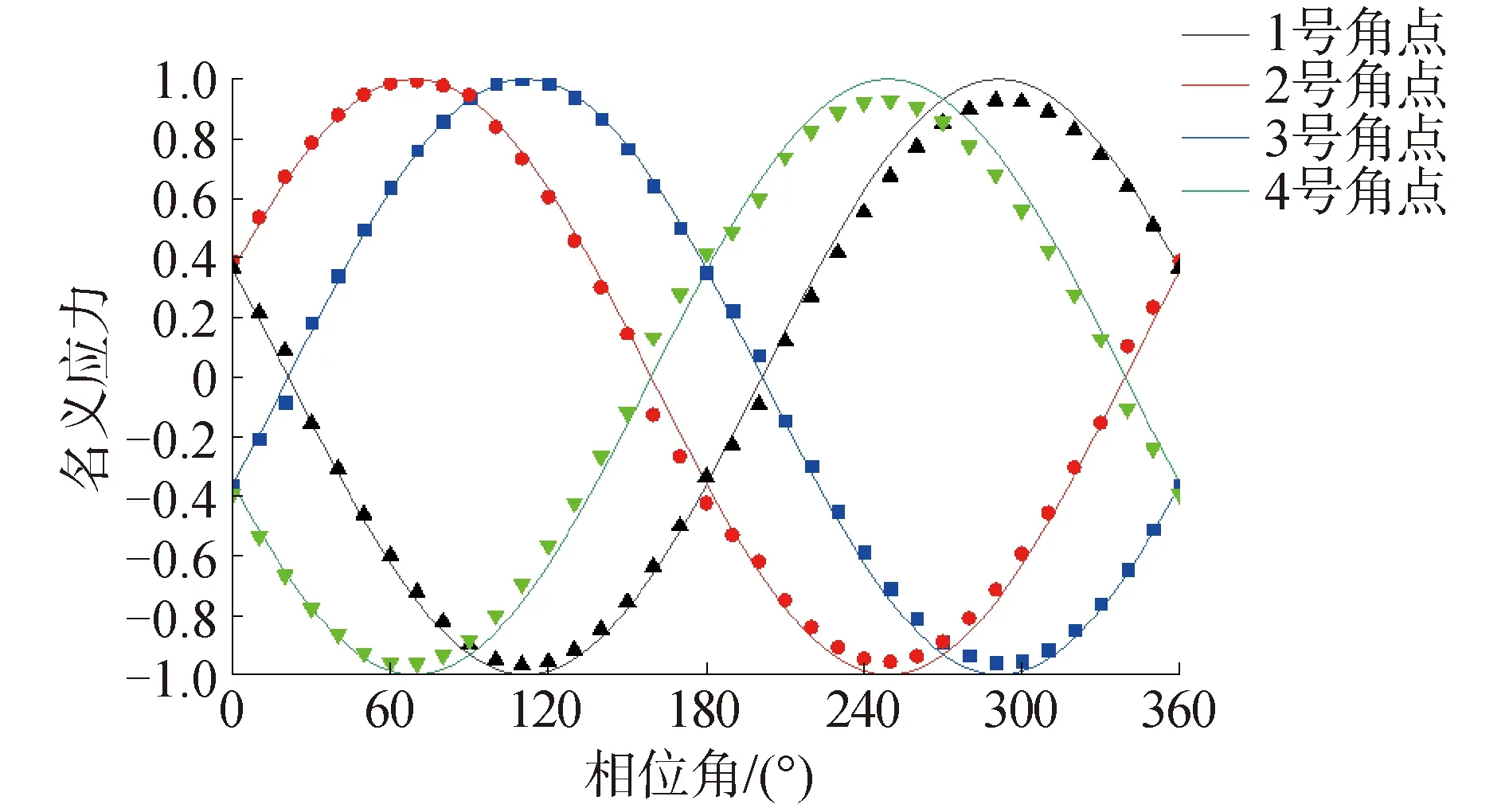
图13 弯曲作用下弹簧结构应力结果

根据上述计算结果可以发现，去除内护套结构后螺旋钢丝在弯曲变形情况下的应力结果与理论计算结构在幅值和变化周期上均保持一致，验证了有限元分析计算结果的可靠性。将图13与图14计算结果后进行比较，发现螺旋钢丝角点应力的相位产生了较大的偏移，这说明在管道受力弯曲状态下，受到内护套结构的支撑作用影响，螺旋钢丝的局部扭转和径向形变受到了约束，从而导致其结构应力响应发生了显著的相位变化。因此，在进行螺旋钢丝滑移形态计算时，考虑圆柱体对螺旋钢丝的支撑与约束作用是有必要的。

4 结论

1)管道弯曲状态下，螺旋钢丝的滑动现象首先发生在φ=π/2,3π/2附近，并向其两侧同时发生扩展，从而带动钢丝整体产生滑动；在螺旋周期内相对滑移量的峰值出现在相位角φ=π/2,3π/2附近，而谷值出现在相位角φ=π,2π附近，证明螺旋钢丝与内护套在管道弯曲方向的端部位置产生了较大的摩擦作用，在局部区域趋于相对约束状态。

2)抗拉铠装层螺旋钢丝呈现“拉伸”和“压缩”的状态，即在φ=π/2,3π/2附近的相对滑移方向与螺旋结构走向基本一致，且在相邻半周期内的滑移方向相反，在φ=π,2π附近螺旋钢丝滑移方向呈现由正到反的快速过渡变化。

3)管道弯曲状态下，螺旋钢丝因受到内部圆柱体的摩擦与支撑作用，限制了其局部扭转和径向形变，将对结构应力响应相位产生较大影响，说明在海洋柔性管道设计中，内部圆柱体对螺旋钢丝的支撑与约束作用是需要考虑的因素。