复合固体推进剂定应变‒温度循环加速试验方法研究
2022-06-07魏小琴李晗赵阳李泽华赵方超
魏小琴,李晗,赵阳,李泽华,赵方超
(1.西南技术工程研究所,重庆 400039;2.中国兵器装备集团弹药贮存环境效应重点实验室,重庆 400039; 3.漠河大气环境材料腐蚀国家野外科学观测研究站,黑龙江 漠河 165301)
固体火箭发动机在库房长期贮存时,由于弹衣包装和壳体包覆,发动机装药一般不直接接触外界环境介质,主要在环境温度的作用下发生损伤。如固体推进剂的粘合剂、某些添加剂热降解,粘合剂与氧化剂相互作用,固体推进剂内部疏松,甚至产生裂纹,固体推进剂/衬层/绝热层/壳体等粘接界面发生脱粘等,引起固体火箭发动机贮存性能下降,甚至失效。
国内外针对固体火箭发动机贮存性能老化试验方法开展了大量研究,部分已形成相关标准。如美国军用规范MIL-R-23139B规定固体火箭发动机在其规定的极限高、低温下分别贮存6个月后,如果静止试验的工作性能符合要求,则其最低贮存寿命为5 a。意大利规定“阿斯派德”导弹固体火箭发动机在71 ℃条件下贮存13周,相当于在意大利的自然环境下贮存7~8 a。我国GJB9722—2020、QJ 2338A—2002等主要采用经验估计与少量贮存固体火箭发动机定期点火试车相结合的概略估计方法,这些方法均需开展发动机静止点火试验,费用较高。
固体火箭发动机在长期贮存过程中,粘接界面发生断裂失效时,通常都断裂在推进剂上,界面处很少出现断裂现象,可近似认为发动机装药老化主要表现为复合固体推进剂老化。QJ 2328A—2002提出无应变推进剂开展4~5个恒定温度加速老化试验方法,并基于传统Arrhenius方程外推固体推进剂贮存寿命。这种方法存在2方面缺陷:1)试验对象大多为方坯药,但研究发现,方坯药与发动机装药贮存寿命有差别。因为固体推进剂内的氧化剂、铝粉等固体颗粒与粘合剂之间总存在空隙,在应变作用下,这些细观缺陷会扩展、聚集,最后发展成宏观裂纹。2)加速老化温度为恒定温度,且认为活化能与温度无关,并未考虑实际贮存温度的昼夜温差、日间温差、季节温差引起推进剂反复膨胀与收缩而出现的裂纹、脆变、汗析等损伤,也忽略了温度对活化能的影响,因此外推结果与实际贮存寿命有偏差。鉴于此,人们开始研究温度循环加速试验方法,但有的试验方法在短时间内反复经历极大温差,可能会加大低温效应和疲劳累积效应,容易出现其他失效模式或失效机理,有的需用至少2 a库房贮存试验结果进行相关性分析,耗时较长。
本文通过仿真计算固体火箭发动机固化降温过程的应变量,结合库房贮存环境温度变化规律,建立了定应变‒温度循环加速试验方法,并开展试验验证。利用指数型老化数学模型和修正Coffin-Manson加速寿命模型,快速预估了复合固体推进剂0.9置信度下的最低贮存寿命,为下一步开展固体火箭发动机装药贮存寿命预估提供研究思路。
1 试验
1.1 样品
三组元复合固体推进剂,主要成分为粘合剂端羟基环氧乙烷四氢呋喃共聚醚,氧化剂高氯酸铵,能量添加剂铝粉,即PET/AP/Al。按GJB 770B—2005 《火药试验方法》B型拉伸样尺寸要求,制成哑铃状试件,尺寸为120 mm×25 mm×10 mm,工程标距为70 mm。
1.2 定应变仿真计算与加载设计
贴壁浇铸的固体火箭发动机在浇铸后的固化降温期间,推进剂药柱的体积会发生收缩。由于推进剂热膨胀系数比壳体材料高1个数量级左右,推进剂收缩受到壳体约束,会产生热应力和热应变,因此必须考虑固化降温对推进剂贮存性能下降的影响。推进剂在温度载荷作用下为多轴应力状态,但多轴应力状态给加速试验模拟带来了较大困难,且试验结果离散性比较大,不宜采用应力加载方式来模拟推进剂在发动机中的受力状态。
推进剂药柱具有近似不可压特性,根据von Mises应变准则,最大von Mises应变可直接用最大延伸率。由于推进剂单轴拉伸应变与多轴应变下的von Mises应变相当接近,误差不超过1%,因此可提取极值点的von Mises应变(可反映药柱承受应力水平高低),直接以单轴拉伸,将应变值与von Mises应变值相等即可,为加速试验模拟带来很大方便。本文应用MSC.PATRAN有限元结构分析软件,建立固体火箭发动机三维有限元模型,仿真计算其固化降温至常温20 ℃的最大应变场,为复合固体推进剂加速老化试验的预应变加载提供支撑。
推进剂属于高分子材料,具有粘弹性特性,并具有拉压同性的特性。为了施加载荷方便,将预应变量以拉应变的方式施加。本文设计了一套复合固体推进剂应变量加载装置(见图1),将复合固体推进剂哑铃型试样工程标距伸长至特定长度,对复合固体推进剂施加预应变。
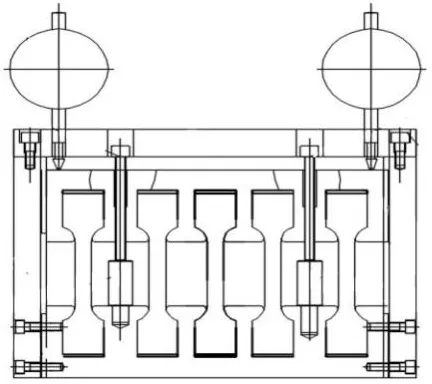
图1 复合固体推进剂定应变加载Fig.1 Constant strain loading of composite solid propellant
1.3 温度循环加速试验设计
首先,构建自然环境条件下的日温度‒时间曲线。研究认为,日温度与时间之间表现为正弦曲线,可用式(1)进行表达。

式中:T表示各时刻自然环境温度值,K;表示1年间自然环境温度最大值,K;表示1年间自然环境温度最小值,K;表示某一自然时刻,即产品贮存在自然环境中的时间点,h。
其次,分析固体火箭发动机为期1 a的库房贮存环境温度数据,计算1 a内日平均温度的最大变化量,见式(2)。

最后,按照库房贮存环境日温度‒时间曲线,在提升温度应力水平的基础上,构建温度循环加速试验曲线的温度‒时间曲线,见式(3)。
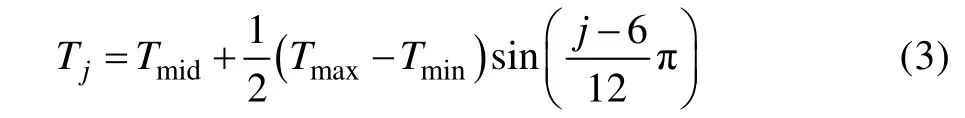
式中:T表示各时刻温度循环加速试验温度值,K;表示温度循环加速试验温度中位值,K;表示温度循环加速试验时刻,h。
温度循环加速试验参数设置包括最高温度、最低温度、温度差Δ、单个循环时长和循环次数。一般而言,在实验室加速应力下,复合固体推进剂失效机理应与实际贮存失效机理一致,因此加速试验剖面的最高温度不应超过复合固体推进剂的最高破坏温度。
根据QJ 2328—2205,PET类复合固体推进剂常用的加速试验温度不超过353 K,与此同时,黑色金属壳体在户外存放时,实测最高局部温度为348 K,由此选择复合固体推进剂温度循环加速试验不超过348 K。由于固体火箭发动机贮存1 a的最大日均温度差为15 K,日温度变化频率为24 h,为了更贴近实际贮存环境温度变化规律,将温度循环加速试验的温度差Δ设为不超过15 K,单个循环时长设为24 h。由此,设置了4组不同应力水平的温度循环加速试验参数,见表1。

表1 复合固体推进剂温度循环加速试验条件设置Tab.1 Setting of temperature cycle accelerated test conditions for composite solid propellant
将已施加预应变的复合固体推进剂拉伸试样在标准环境(296 K、RH值为55%)中调节3 h,放入防静电铝塑袋,利用真空封装机进行密封后,分别放入4个防爆型温度循环试验箱中,按照表1设置试验条件,开展温度循环加速试验。某应力水平下的加速试验曲线见图2。

图2 某应力水平下温度循环加速试验曲线Fig.2 Temperature cycle accelerated test curve at a certain stress level
在9~10个不同老化周期,从4个试验箱各取出1个加载工装,拆下5个平行拉伸样,在标准环境中调节3 h。然后根据GJB 770A—1997方法413.1《抗拉强度、断裂强度、伸长率和断裂伸长率 单向拉伸法》,利用万能材料试验机,以50 mm/min速率测试最大抗拉强度,并采用格鲁布斯法,剔除异常数据后,以最大抗拉强度平均值作为该加速试验时间的最大抗拉强度。
2 结果与讨论
2.1 定应变仿真计算结果
模拟的固体火箭发动机药型为两段式结构,前段为圆管型,后段为星形结构,几何构型具有循环对称性,温度载荷也具有轴对称性,因此其响应也必然是轴对称的。选取发动机药柱轴对称的1/10,将其划分为三维有限元模型,并对药柱由零应力温度(68 ℃)固化降温至常温(20 ℃)的整个过程进行数值仿真,结果见图3。
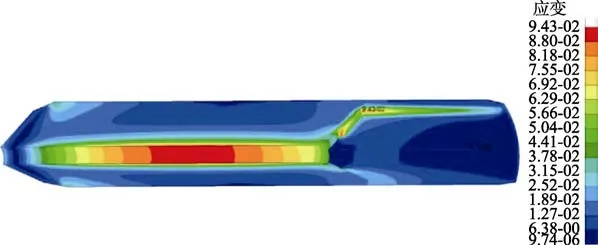
图3 常温20 ℃时复合固体推进剂药柱von Mises应变场分布云图Fig.3 Cloud diagram of von Mises strain field distribution of composite solid propellant grains at room temperature 20 ℃
从图3可知,常温20 ℃载荷导致推进剂药柱收缩,推进剂药柱前段圆柱中部、圆管段与星角段相交处中部、后段星角段前端均存在von Mises应变集中,在发动机药柱前圆管段中部对应处的von Mises应变为9.2%,圆管段与星角段相交处中部的von Mises应变为9.3%,后段星角前端的von Mises应变为9.4%。
在易于施加载荷且仿真误差小的基础上,以极值点von Mises应变量为特征参量,将后段星角前端部位的9.4%应变量作为最大的贮存应力等效加载量。由于推进剂药柱的应力松弛和应变蠕变始终存在,本文采用的固定应变量方式只模拟了应力松弛效应,未模拟应变蠕变效应,可能存在一定误差。
2.2 定应变加载结果
根据仿真分析结果,复合固体推进剂固化降温过程的最大应变量为9.4%。复合固体推进剂哑铃型试样工程标距为70 mm,计算拉应变的伸长量为6.58 mm。将5件复合固体推进剂哑铃型试样放入一套定应变加载工装内,使试样一端固定在下横梁框架中,另一端固定在上横梁框架中。通过内六角扳手调节拉紧滑块上的2个加载螺杆,将拉伸试样的工程标距由70 mm伸长至76.58 mm,并由百分表的示数来判断固体推进剂应变量加载大小是否达到设定的形变值,控制精度可达0.01 mm。再以数显游标卡尺复测各试样标距,保证了加载的准确性。
2.3 温度循环加速试验结果分析
固体火箭发动机装药在长期贮存时,贮存性能变化最为明显的就是固体推进剂的力学性能,因此人们常常通过监测固体推进剂力学性能的好坏来预估发动机装药贮存寿命。力学性能测试结果表明,在整个试验过程中,最大伸长率基本上在初始值附近波动,虽然最终也会低于初始值,但下降幅度仅为10%~17%,不作为特征性能参数。随着老化时间延长,4组不同应力水平的最大抗拉强度呈现出单调下降的趋势,可作为特征性能参数。由此,采用初值化法,对4组不同应力水平的PET推进剂最大抗拉强度数据进行无量纲化处理,获得最大拉伸强度保留率变化数据(),见表2。
从表2可知,随着老化时间延长,4组应力水平的最大抗拉强度保留率在老化前期下降很快。在老化7 d时,下降12%~31%。随后性能下降速率变慢,呈现波动下降趋势,与复合固体推进剂实际长期贮存的最大抗拉强度保留率变化规律一致,说明本文建立的温度循环试验方法并未改变其老化机理。4组应力水平的最大抗拉强度保留率下降程度排序为:应力水平1>应力水平2>应力水平3>应力水平4,说明最大抗拉强度保留率与温度高度相关,也即试验温度越高,最大抗拉强度保留率下降越快。

表2 复合固体推进剂4组应力水平的最大抗拉强度保留率数据Tab.2 Maximum tensile strength retention rate of composite solid propellant at different stress levels
根据QJ 2328A—2005,选择指数模型作为复合固体推进剂性能老化模型:

式中:P为时刻的老化特征参数值,即最大抗拉强度保留率();为常数;为速率常数,d;为老化时间,d。
利用上述模型,对表2数据进行拟合,获得反应速率常数和相关系数。根据相关系数检验临界值表,取自由度为‒2,分别给出查表值,见表3。

表3 复合固体推进剂不同应力水平的性能老化数学模型拟合参数与可靠寿命Tab.3 Performance degradation model fitting parameters and reliable life of composite solid propellants at different stress levels
从表3可知,>,说明置信度为0.9时,复合固体推进剂在4组温度循环加速试验条件下的最大抗拉强度保留率均符合指数型性能老化数学模型。

加速寿命模型一般性的基本假设为:在各加速应力水平下,产品的失效机理保持不变;存在有规律的加速过程,产品性能退化量或寿命特征量与应力之间存在一个确定的函数关系,即加速模型的存在性;在各加速应力水平下,产品的退化过程服从同族随机过程,即应力水平变化时,产品退化过程模型的类型不变,改变的只是模型的参数。
对于固体推进剂,上述一般性的基本假设可以进一步明确。
1)在温度循环应力下,固体推进剂寿命分布服从威布尔分布,分布函数为:

式中:m为形状参数,m>0;η为尺度参数(特征寿命),η>0。
2)推进剂剩余寿命仅依赖于当时已累积失效部分和当时应力水平,而与累积方式无关。
3)在贮存环境应力水平和4组加速试验应力水平下,固体推进剂失效机理不变,也即威布尔分布的形状参数不变,即====。
Coffin-Manson模型用来模拟温度循环应力导致的产品疲劳失效,已被成功用于模拟焊点受到连续温度冲击后的裂纹扩展过程。由于固体推进剂温度循环试验条件为4组,不满足参数法的使用条件,因此采用非参数方法,利用修正Coffin-Manson模型,对复合固体推进剂库房贮存寿命进行计算:

式中:为临界循环次数,也即贮存寿命,d;为循环频率=1/=1/24;Δ为温差,K;()为温度循环试验中最高温度时的阿伦尼斯方程,()=e;为波兹曼常数,=8.6173×10J/K;为常数;为温度循环试验最高温度的活化能,kJ/mol;为温度循环试验中最高温度,K。
对于修正的Coffin-Manson模型,两边取对数,并使之线性化,整理后得到:

按下述步骤,计算某一置信度下固体推进剂的最低库房贮存寿命:
1)针对4组加速应力水平试验的置信度0.9下的最低加速寿命时间(也即临界循环次数),对线性化后的修正Coffin-Manson模型进行多元线性回归分析,计算该模型的未知参数、、、。
2)将库房贮存的应力水平值代入修正Coffin-Manson模型,即可得到库房贮存试验中置信度0.9的最低贮存寿命。
由此将表3的4组温度循环加速试验数据代入修正Coffin-Manson模型,见表4。

表4 复合固体推进剂不同应力水平的修正Coffin-Manson模型参数Tab.4 Modified Coffin-Manson model parameters of composite solid propellants at different stress levels
利用多元回归分析方法,计算置信度0.9的修正Coffin-Manson模型中的未知参数值,计算结果见表4,即固体推进剂置信度0.9的修正Coffin-Manson模型为:

当固体火箭发动机贮存期内最高温度为298 K(25 ℃),年均温差为15 K时,代入上述修正Coffin-Manson模型中,求得该贮存环境下置信度0.9时的复合固体推进剂最低库房贮存寿命为20 a。
3 结论
1)在兼顾模拟性和加速性的基础上,建立了复合固体推进剂定应变–温度循环加速试验方法,其特征老化性能参数最大抗拉强度随时间的延长而下降,与实际长期贮存试验的性能变化规律一致,并未改变其贮存老化机理。
2)基于指数型性能老化数学模型和修正Coffin-Manson加速寿命模型,利用多元回归分析方法,在置信度为0.9时,快速评估固体推进剂的最高贮存温度为298 K(25 ℃),年平均最大温差为15 K时的最低库房贮存寿命为20 a。
