高速公路路基边坡的冲刷与防护措施分析

2022-06-07高英树

交通科技与管理 2022年10期

高英树

摘要文章利用离散元PFC建立路基边坡模型，明确压实度、冲刷速度与冲刷时间对路基边坡冲刷深度的影响。结论如下：砂性土路基边坡冲刷深度主要受压实度、冲刷时间和冲刷速度的影响。随着压实度增加砂性土边坡模型中颗粒位移和冲刷量逐渐减小;从模拟结果可知，砂性土边坡冲刷深度随着压实度的增大逐渐降低，随着冲刷时间与冲刷速度的减小，路基边坡的冲刷深度逐渐减低。

关键词路基边坡;冲刷;防护;PFC数值模拟

中图分类号 P64222 文献标识码 A 文章编号 2096-8949（2022）10-0175-03

0 引言

我国关于公路水毁灾害研究较多，内容比较广泛。公路水毁的研究主要集中在水毁产生的原因和防护措施两个方面。针对定性公路水毁原因以及基于实践提出的防护措施的研究存在不足，分析不够深入。

Tsuji等[1]最先使用离散元（PFC）方法模拟气体在固体介质颗粒中的运动。Shamy等[2]首次在岩土工程中使用流固耦合分析方法研究渗流影响。黄润秋[3]研究云南山区的公路水毁破坏特点，划分水毁环境，进行预报并给出相应防灾对策。熊传祥[4]使用流固耦合的分析方法，在模型边界条件上设置压力实行降雨，结果表明离散元（PFC）计算中使用流固耦合方法研究崩岗的过程是可行的。宋朋燃等[5]利用流固耦合的分析方法对降雨条件下边坡的冲刷建立离散元（PFC）三维模型，对边坡冲刷侵蚀的作用过程进行整理归纳，分析降雨过程中路基边坡的冲刷深度与水流的侵蚀力分布。刘兴旺[6]研究路基边坡雨水入渗过程与稳定状态，通过分析路基边坡土体中渗透力的作用完成了不同降雨情况下的稳定性研究。

离散元（PFC）仿真既可以用在不连续的大变形中，也可应用在土颗粒受力与运动中。鉴于此，利用离散元（PFC）计算理论建立路基边坡模型，仿真模型建立的重点是建模过程和参数选取，选取坡比1∶1.5路基边坡，明确压实度、冲刷速度与冲刷时间对路基边坡冲刷深度的影响。

1 路基边坡冲刷特性的仿真模拟

1.1 计算数值模型

模型如图1，材料参数如表1所示。

建立模型第一步使土颗粒处于密实状态，接下来让所有粒子的半径均匀减小，目的是使试样达到目标初始压应力;下一步将浮点粒子与附近接触少于三个的粒子删除，通过粒子的删除得到需要的孔隙率，此处模型孔隙率为0.1;再根据不同的压实度要求将试样中的小的颗粒删除，得到需要的边坡模型;最后给土颗粒施加一个冲刷速度，在冲刷条件下边坡颗粒被剥落、搬移，模拟出路基边坡的冲刷过程。考虑到计算机的计算能力，尽量在减小粒子尺寸的条件下将生成模型放大，目的是多生成土颗粒方便路基边坡冲刷破坏的模拟。最终土颗粒的最小半径为0.8 mm，最大为12 mm，路基边坡生成4 125个颗粒单元。

1.2 实现过程

路基边坡的冲刷深度受土体性质、压实度、冲刷时间与速度的影响比较大，因此，路基边坡模拟将考虑不同因素对路基边坡的冲刷影响。通过PFC内置命令可以在生成模型时控制生成粒子的孔隙率，由于孔隙率与压实度的关系得到压实度。PFC软件内置有Fish程序语言，通过Fish程序语言中的条件循环函数在模拟实验开始时选择边坡表面颗粒、并通过命令赋予颗粒的初始速度，再利用函数控制粒子的重度，使其不断地增加。以步长为循环条件来重复识别边坡表面粒子使其达到模拟实际边坡冲刷效果，通过命令获取冲刷一定时间后边坡表面球体到倾斜墙体的距离。当边坡表面上颗粒遇水冲刷时，水会带给土颗粒一定初速度，并且水渗入土体。随着土体逐渐变得饱和，土颗粒重度也会随之增大，所以增加一定速度与重度可以合理地模拟冲刷。

路基边坡冲刷过程实现：

（1）边坡颗粒模型的生成。

（2）对所有土颗粒赋予接触。

（3）对路基边坡坡面上的土颗粒进行识别、分组与假设。

（4）删除路基边坡模型试样的顶墙，设定边坡便面颗粒的增重与速度，开始计算。

模型中边坡土体选取砂性土，边坡压实度为80%、85%和90%，在水流冲刷速度分别为0.1 cm/s、0.16 cm/s和0.2 cm/s的条件下，给出路基边坡的冲刷过程结果，文中选取坡比1∶1.5边坡模型，给出路基边坡冲刷过程中的不同形态，每过程以100 000步为单位。

2 模拟结果分析

2.1 压实度对边坡冲刷深度影响

路基边坡冲刷深度与压实度大小有关，路基边坡上从坡顶到坡底均匀设置测量点，其他条件相同情况下，测得不同压实度的路基边坡冲刷深度。

图2可以看出，砂性土边坡的冲刷深度较大，压实度与冲刷深度的变化趋势相反。在同一个测点处，80%压实度边坡的冲刷深度最大，85%压实度边坡的冲刷深度较前一压实度的冲刷深度小，90%压实度边坡的冲刷深度最小，表明随着压实度的增大路基边坡各点处的冲刷深度逐渐减小。

2.2 冲刷时间对路基边坡冲刷深度的影响

由图3可知，砂性土路基边坡的冲刷深度都随着冲刷时间的增大呈现增长趋势。

0～3 min时间内曲线增长缓慢，路基边坡的冲刷深度较小，3～6 min曲线增长变化剧烈，路基边坡冲刷深度骤增，6 min以后曲线继续增长，增长趋势减缓，邊坡冲刷深度缓慢增大。

2.3 冲刷速度对路基边坡冲刷深度的影响

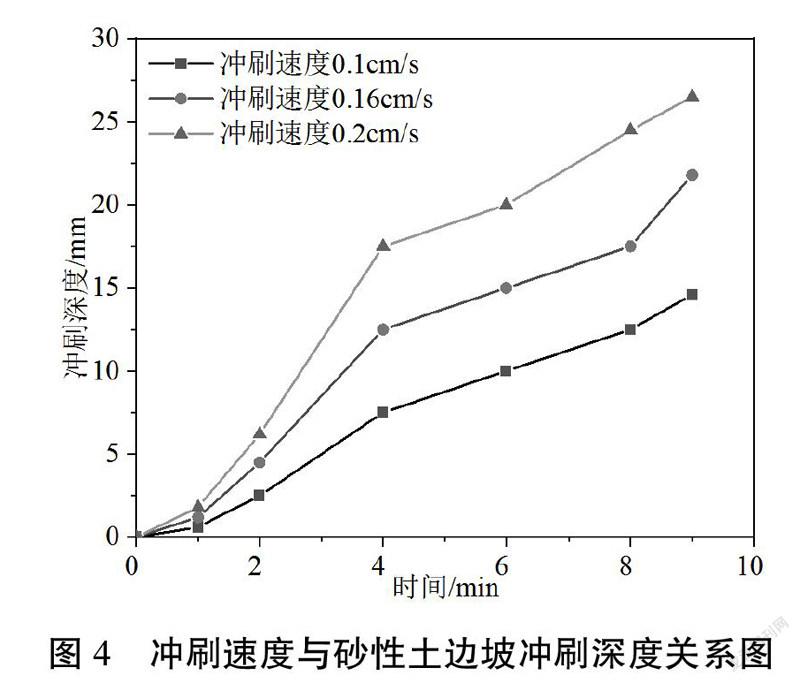
图4是砂性土路基边坡冲刷深度与冲刷速度的变化曲线图。

由图可知，边坡冲刷深度都呈现递增变化，随着水流冲刷速度的增大路基边坡的冲刷深度呈现增加趋势。相同时间内，0.2 cm/s流速条件下路基边坡的冲刷深度最大，增长迅速，水流速度降到0.16 cm/s时，冲刷深度明显减小，曲线增长变慢，0.1 cm/s流速下边坡冲刷深度最小，相比于0.2 cm/s流速冲刷深度几乎减小了一倍。由此可见，随着水流冲刷速度减小路基边坡冲刷深度逐渐降低。

3 高速公路路基边坡冲刷防护措施

路基边坡冲刷破坏的稳定性评价是一个具有复杂性的评价过程，主要表现为：影响路基边坡稳定性的因素较多，各因素相互影响共同作用;评价指标的定义标准形式多样;缺乏足够评价信息资料。因此，路基边坡冲刷稳定性破坏研究具有不确定性。

3.1 排水防护技术

公路排水防护工程的主要措施有边沟、截水沟、排水沟、急流槽与盲沟等。其中边沟、截水沟与排水沟是低等级公路中最常见的防护措施。

3.2 工程防护技术

公路边坡工程防护指使用水泥、砂浆、石灰等材料展开的防护，护面墙和植被混凝土这两种形式是最常见的技术。护面墙通常情况下被用于易风化的软质岩石与相对破碎的岩石边坡的防护，是比较常见的上边坡的防护形式，作用是减免边坡表面的侵蚀、持续风化以及部分坍塌与滑坡等破坏。护面墙的缺点是不能承受墙后边坡土体的主动土压力，故边坡的稳定性限制了护面墙的使用。常见边坡护面墙的形式有拱式、孔窗式等。

3.3 植被混凝土坡面防护

植物坡面防护的作用机理可分为植被根系的力学作用和植被的水文效应两大部分，两个方面共同协作增加边坡土体的稳定性。该方法是一种新兴起的防护技术，由植被防护、混凝土防护作用，同时拥有两种防护的优点。植被混凝土防护因其混合防护形式的特点应用范围广，既能用于风化岩石边坡也可以用于土质边坡的冲刷防护。为了植被的优良生长以及坡面的观赏性防护结构，结合形式应具有灵活性。骨架防护属于植被混凝土防护的一种形式，通常设置在坡度较缓、相对稳定的边坡，采用混凝土或者浆砌片石修建成框架，将草种在其中。这种边坡综合防护措施既能减少路基边坡的冲刷破坏也可以提高坡面的观赏性。其防护形式主要有：

（1）种草。适用于边坡稳定、坡面冲刷轻微路堤或路堑边坡，一般要求边坡坡度不陡于1∶1，边坡坡面水径流速度不超过0.6 m/s，长期浸水边坡不适用。

（2）铺草皮。适用于各种土质边坡，特别是坡面冲刷比较严重、边坡较陡（可达60°）、径流速度达0.6 m/s时。主要有平铺、水平叠铺、垂直坡面或与坡面成一半坡脚的倾斜叠置，以及采用片石等铺砌成方格或拱形边框、方格内铺草皮等。

（3）植树。适用于各种土质边坡和风化极严重的岩石边坡，边坡坡度不陡于1∶1.5，在路基边坡和漫水河滩上种植植物，对于加固路基与防护河岸具有良好的效果。可以降低水流速，种在河滩上可促使泥沙淤积，防止水流直接冲刷路堤。植树最好与植草相结合。高等级公路边坡上严禁种乔木。

4 结论

利用PFC模拟软件对路基边坡冲刷进行仿真，明确路基边坡冲刷特点和影响因素。路基边坡仿真模型建立的重点是建模过程和参数选取，结论如下：

（1）砂性土路基边坡颗粒的位移和冲刷量较大，随着压实度的增加砂性土边坡模型中颗粒的位移和冲刷量逐渐减小。随着时间的增大边坡模型颗粒的位移和冲刷量增加。

（2）路基边坡的冲刷深度主要受压实度、冲刷时间和冲刷速度的影响。从模拟结果可知，砂性土边坡冲刷深度的增大变化较大，路基边坡冲刷深度随着压实度的增大逐渐降低，随着冲刷时间与冲刷速度的减小，路基边坡的冲刷深度逐渐减低。

（3）路基边坡防护措施主要可分为，排水防护与工程防护技术，宜根据实际情况采取相应的坡面防护措施。

参考文献

[1]Tsuji Y， Kawaguchi T， Tanaka T. Discrete particle simu-lation of two-dimensional fluidized bed [J]. Powder Technology， 1993（1）： 79-87.

[2]Shamy U E， Zeghal M. Coupled continuum-discrete model for saturated granular soils[J]. Journal of Engineering Mechan-ics， 2005（4）： 413-426.

[3]黃润秋. 中国西部地区典型岩质滑坡机理研究[J]. 地球科学进展， 2004（3）： 443-450.