供电网络线损计算研究综述

2022-06-06程绪可王赫妍

沈阳工程学院学报（自然科学版） 2022年2期

叶臻，叶鹏，程绪可，李忱，王赫妍

（1.沈阳工程学院电力学院，辽宁沈阳 110136；2.国网辽宁省电力有限公司电力科学研究院，辽宁沈阳 110006；3.国网辽宁省电力有限公司计量中心，辽宁沈阳 110168）

在当前时代背景下，整个社会对清洁的二次能源——电能的需求越来越旺盛。由于能源的逐渐短缺，导致每个国家都更加注重在电能的开发与运输方面的建设。电能在运输过程中将会产生一定的损耗，而这些损耗通常被称为线损。线损与多种因素有关，如传输距离、电线直径与材料、途径区域温度等。

通过对线损的计算结果的总结与分析，不但可以对供电企业的管理水平作出合理化判定，还可以分析出企业的经济运营状况。此外，社会的进步使得不能继续依靠高耗能行业拉动售电量增长，电量和收入的下滑与成本刚性增长量间的矛盾越发尖锐。我国目前的线损率情况不容乐观，平均线损率与欧洲国家平均线损率勉强持平，但与亚洲一些发达国家之间仍有较大差距。提高专业线损的计算管理能力是电力企业加强经营管理的必经之路［1］。

通过查阅国内外大量的线损相关文献，针对目前几种常见的线损理论计算方法的模型及研究现状进行阐述，说明了应用现状及优缺点，并列举了若干种上述理论线损计算的改进模型，再对目前线损计算的研究热点方向进行说明，最后结合国内外研究现状，对线损计算的未来进行了展望。

1 线损的定义、基本分类及管理方式

1.1 线损的定义

线损主要是指从发电厂一直传输到客户，电能在运输、变电、配电等一系列过程中，由于各方面因素的影响而产生的损耗［2］。这些损耗通常包括两个方面：一是自然线损，即电能传输时无法规避的一种电能损失；二是管理线损，即由于供售电量统计存在差异、人工操作失误等而产生的电能损失。

具体来说，电能在传输过程中产生线损的原因有以下几方面：

1）电阻作用：对电能进行传输时，首先需要克服源于导体自身产生的电阻，在此过程中将会耗费大量的电能，通常体现为导体温度升高。

2）磁场作用：变压器在进行升压或者降压的过程中，必须要搭建并维持交变磁场，只有这样才可以确保变压器正常运行。而对于电动机而言，需要搭建并维持旋转磁场，这样才可以正常运转。

3）管理方面：供电企业在开展输配电管理工作的过程中，由于各方面因素的影响，同样会导致电能产生一定的损耗。它受每个管理部门的手段和条件所限，或者在电网中存在用户违章用电和偷电、电网元件漏电、电表更换不及时、抄表人员的漏抄、错抄等现象而造成的电能损失。

1.2 线损的基本分类

若以损耗组成为标准，那么线损可以细化为固定损耗、可变损耗、其他损耗3 类。前两种类型均属于自然损耗，通常也被定义为无法避免的一种损耗；而对于其他损耗来讲，主要是在管理方面所产生的损耗［3］。

1）固定损耗：主要包括变压器的铁损及表计电压线圈损耗。

2）可变损耗：主要包括导线损耗、变压器铜损。

3）其他损耗：一般情况下，其他损耗主要是供电企业的管理人员由于操作失误或者管理不当而导致电能在传输过程中产生的一系列损失。

按照线损的构成以及不同的分类方法，构建一个框图来表示它们之间的关系，如图1所示。

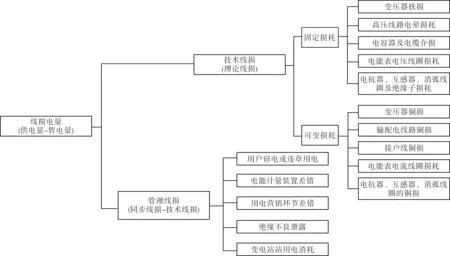
图1 各种线损分类及相互关系

1.3 线损的四分管理

供电企业主要对线损实行分区、分压、分元件、分台区的四分管理［4］，其主旨是通过精确定位线损异常点，排查高线损元件，并对线路进行科学化监测与分析，综合提高供电网络关于计算线损电量与降低线损量的能力。

2 传统线损理论计算

线损理论计算是根据电网的结构参数与运行参数，运用相适应的理论公式计算出理论线损电量等数值，并进行线损的分析与评估。

熟练掌握各线损的理论计算方法，有助于深入理解线损的构成。可以针对不同的计算对象给出相适应的线损理论计算方法。本文列出了目前应用比较广泛的几种线路理论运算方式。

2.1 均方根电流法

该种电能损耗计算方式已经应用多年，属于一种常规方式，主要运用代表日的均方根对电能损耗进行运算［5］，具体计算公式如下：

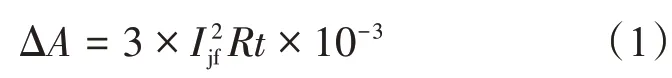
式中，t为运行时间；ΔA表示在时间t内所消耗的电能；R表示被测电子元件的电阻值；Ijf为均方根电流值。

均方根电流值可以通过日均方根电流来计算，其具体计算方法为

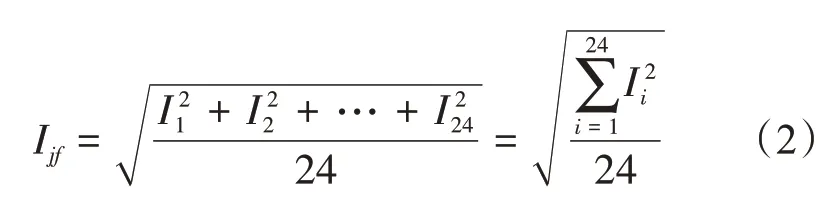
式中，Ii为代表日24个整点通过该元件的电流。

均方根电流法的计算过程十分简单，只需要对代表日各时间节点的功率或电量进行统计就可以换算出配电网的损耗［6］。然而，该方法也存在明显的不足之处，首先，有些电力元件的负荷节点与其均方根电流值并不具有完全固定的关系，例如无负荷的变压器；其次，线损的计算是通过对典型日各时间节点的统计值来估算的，而典型日的电量损耗情况对于长期的电量损耗情况来说，是否具有充分的代表是需要具体分析的。由于该方法的计算精度受限条件较多，直接影响了国内外学者对于此方法的研究与应用。

2.2 平均电流法

平均电流法从原理上来说是对均方根电流法的一种优化和改进，是在均方根电流的基础上，综合考虑电力负荷的形状系数，用其修正准确性［7］。形状系数k可以表示为

式中，Iav为典型日负荷电流的平均值。

由于形状系数具有一定的规律性，可以通过对历史数据的统计得到。因此，当典型日负荷数据无法获取时，就可以通过形状系数来进行较为准确的估算，然后再参照负载率、最小负载率这两个参数进行更深入的运算［8］：

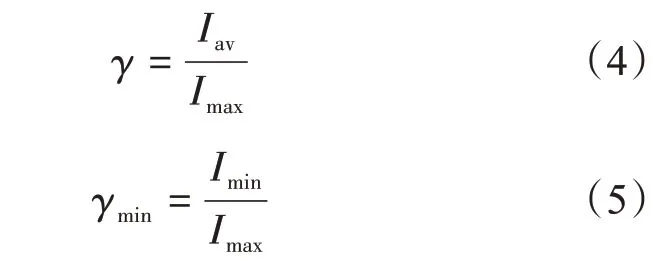
式中，γ为负载率；γmin为最小负载率。

负载波动损耗系数KT与负载曲线形状系数k的关系为KT=k2。

1）如果γ≥0.5，则认为负荷曲线是按直线变化的，此时形状系数k表示为

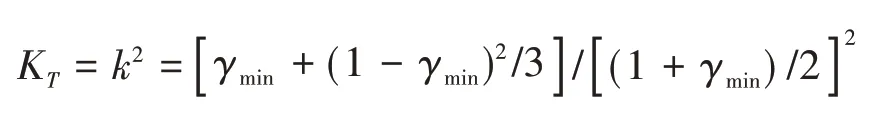
2）如果γ≤0.5，则认为负荷曲线是按二阶梯变化的，此时形状系数k可以表示为

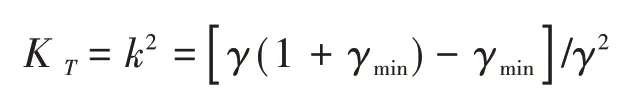
由此可以直接得出配电网线损的计算公式：

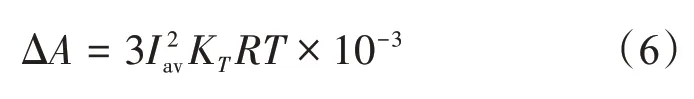
平均电流法不再依赖于典型日功率的准确测量，而采用电量作为统计基础，因而可以取得较高的计算精度。但这种方法也不可避免地带来了一些问题：①形状系数的获取必须建立在大量历史数据的统计基础上；②计算公式中的电压值通常采用平均电压，但实际配电网中的电压是有波动的，在很大程度上影响了计算的准确性。文献［9］在基于假设条件不变的情况下，利用实测负荷电流曲线来确定其形状系数，并根据电量记录改进了负荷曲线的形状系数，这样就减少了典型日选取所带来的误差，同时考虑了配变空载电流或空载损耗的影响，修正了铜损的计算。

2.3 等值电阻法

为了弥补以上两种方法在计算精度上的不足，有人提出了等值电阻法，其基本思路是运用合理化的方式构建一个虚拟等值电阻，用以模拟变压器电阻及线路电阻，一方面可以更加方便、快捷地进行运算，另一方面可以规避电网数据较多、计算难度较高的问题［10］。

在应用等值电阻法之前，需要进行如下假设：①对于负载分布规律而言，其与负载节点装设的变压器额定容量之间为正比例关系，通俗来讲就是不同配电变压器的负载率完全相等；②各个节点的功率因数相同；③各个节点的电压值相同，不考虑电压降落。

在上述条件下，配电线路的电阻为

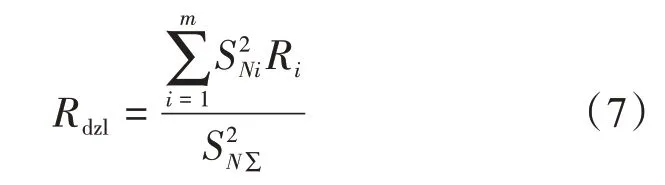
相应的配电变压器等值电阻为

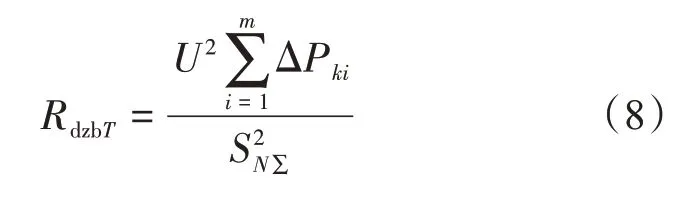
式中，Rdzl为线路的等值电阻；SNi为第i段线路的配电变压器额定容量；Ri为第i段线路的电阻值；SN∑为该条配电线路总配电变压器额定容量；RdzbT为配电变压器的等值电阻（铜损）；ΔPki为第i台配电变压器的额定短路损耗；U为各配电变压器节点的电压。

等值电阻法对参数的测量要求比较低，数据的获取难度较小，操作方便快捷。但这种方法是建立在大量假设的基础上的，而这些假设与实际电网的运行情况多少会有些区别，因而会给计算带来不确定性因素，使得计算精度难以保证。文献［11］首先从多个层面、多个维度对低压配电网0.4 kV 及10 kV 的研究现状进行了剖析，然后比较了两个电压等级下影响各种方法准确度的因素，并对等值电阻法进行了改进，但是该改进方法主要是针对辐射状配电网的，未将环网考虑在内；其次，为了提高计算速度，将计算过程中的一些变量设成常量，对计算结果的影响程度还需要进一步探讨。文献［12］为了弱化等值电阻法的假设条件，通过引入平均电流损耗时间的概念，利用电流的代数平均值求电能损耗，削弱了偶然的畸变值对最终计算值的影响，在一定程度上提高了计算的精确性。

2.4 最大电流法

该方法主要是依据均方根电流和最大电流之间存在的等效关系对电能实际损耗进行分析与运算，为了提高所求结果的准确性，还引入了损失因素F，具体计算公式如下［13］：

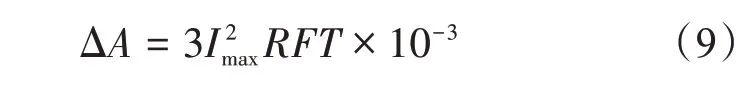
式中，Imax为代表日最大负载电流；F为代表日损失因数，

上述方法虽然在理论上可行，然而在实践操作中过程繁琐，因此电力公司主要利用该方法对主要计算方法进行辅助性计算。该方法能在主要方法不适用的情况下对其进行补充以实现更高精度的线路电损计算，可以为降损方法提供相关指导。

2.5 潮流计算方法

潮流法的精度高，能较好地处理10 kV 配电网中的环网问题，适用于配电网线损的深入分析。但是，原始数据的采集工作量较大，差错概率大，个别情况下可能存在计算不收敛问题，且不能考虑环温和电流温升对电阻的影响，计算速度慢。当电网结构复杂，节点数过多，收集的参数、数据整理困难时，难以采用该方法。针对潮流计算所需原始数据较多的问题，诸多学者进行了研究。文献［14］提出了匹配潮流法，文献［15］提出了改进迭代法，文献［16］提出了区间算法。文献［17］针对三相不平衡对配网造成的损耗的不可忽略性，提出一种利用PQU 负荷曲线分相潮流算法，改进了传统算法采用简化计算造成的较大误差。文献［18］构建了一种高斯-牛顿法计算模型，首先对配电网进行潮流计算，再进行理论线损的计算，这使潮流计算收敛更快，得出的结果也更加精确，但是需要采集每个节点的数据，容易产生误差且数据庞大。但对于复杂配电网而言，这些方法的可操作性较低。

2.6 线损计算方法比较

为了更清晰地表达当前几种主要的线损计算方法的优缺点以及适用性，列出表1进行比较。

表1 传统线损计算方法比较

2.7 小结

以上列举了几种常见的线损理论计算方法，诸如此类的线损理论计算方法还有台区损失率法以及近年来兴起的基于机器学习的线损计算方法等。

在实际的配电网网损分析中，对于35 kV 及以上的电网，应采用均方根电流法和潮流法计算电量损耗。中压配电网（6 kV～20 kV）由于网络结构复杂，节点和元件多，最好采用基于配变容量的等值电阻法和前推回代法［26］。对于低压台区，其电网结构十分繁琐、复杂，并且不具有完整、详细的线路参数以及负荷数据，因此在对线损进行运算的过程中，一般运用近似算法，如电压损失法、等值电阻法等。

3 理论线损计算新进展

通过研读各类文献可以发现，现有的线损理论计算成果颇丰，针对不同的配电网构建不同的计算模型，并且有针对性的提出一些降损措施。但是在计算模型搭建的过程中，存在一些假设条件或者忽略一些实际的影响线损因素，这样的近似计算使线损的精确度得不到很好的保障。

随着供电线路的完善和供电系统的不断成熟，越来越多的线损计算方法被研究出来。与此同时，发达的供电网络和在线监测技术也为线损计算提供了及时、精确的供电数据，为计算线损提供了数据保障［27］。因此，随着计算方法和数据获取两方面的进步，供电线路的计算结果精确度得到了质的提升。最近几年，在大数据技术水平不断提升以及智能算法广泛应用的促进之下，诞生了大量理论线损智能算法［28］。利用理论线损智能算法可以从根本上提高计算结果的精度，然而这对于数据量和供电线路的成熟度和完善化有较高的要求，因此只适用于新型供电线路中，在传统的供电线路上并不适用此种计算方法。文献［29］在对线损进行运算的过程中主要应用了层次聚类法，通过合理化的方式对台区进行聚类，以此为基础搭建随机森林估计模型和决策树分类模型，再对台区线损率进行求解。文献［30］以相关理论为指导，搭建了一种新型运算方式，即复合学习算法，是依托于粒子群算法和回归神经网络算法而提出的，主要根据历史数据样本搭建线损运算模型。文献［31］提出改进K-Means聚类算法对原始数据进行分类，建立LM 算法优化的BP神经网络模型，针对每类样本进行学习训练，揭示了不同电气特征参数下台区线损率的变化规律。文献［32］以现有研究方式为基础，提出了一种基于向量回归的线损运算方式，借助支持向量回归的拟合特性分析出线损和特征参数之间所存在的具体规律，然后再对线损进行求解。文献［33］运用对抗生成网络弥补线损计算数据偏少的情况，再利用BP 神经网络进行线损率预测，大大提高线损率预测的准确性。文献［34］利用RBF 神经网络优异的非线性拟合特性，量化分析了三相不平衡所带来的附加损耗。

4 综述分析及展望

就研究的整体情况而言，现有的线损理论计算，也就是对电力网中的元件搭建不同的数学模型进行线损计算已经成果颇丰。近些年，计算方法已经很少出现突破性的进展，现有的多数研究都是在前文列举的几种理论计算方法上进行优化。同时，近年来随着大数据与人工智能技术的不断发展，给各行各业都带来了冲击，电力行业也不例外。随着智能电能表的普及，电网在收集数据的时效性能力方面进一步加强。

随着电网智能化水平的提高，数据的获取变得不像以往那么困难。现有的难题已经变成了如何利用海量的数据去构建高精度的线损计算模型问题。利用智能算法可以为线损的海量数据提供新思路，智能算法可以摆脱传统线损理论计算中模型的简化及一系列假设所造成的误差。人工智能算法可以直接构造出“输入值-输出值”之间的映射，而映射过程需要通过大量的历史数据训练得到［35］，理论上历史数据样本越多，计算结果也越精确。但是，对于输入值（特征值）的选取依然缺乏足够的依据，不够全面。对于不同结构的电网或台区，需要重新进行线损模型的构建。因此，利用智能算法进行线损计算有着进一步研究的必要性。