基于Retinex算法的数字航空影像色彩校正研究
2022-06-06张烁王凤艳王明常吴翔
张烁,王凤艳,王明常,吴翔
吉林大学 地球探测科学与技术学院,长春 130026
0 引言
在摄影测量工作中,数字航空影像的获取一直是最基本也是最关键的一步。高质量影像会大大提高航空遥感影像建模、解译等工作的质量。然而,在影像获取过程中,受大气折光、相机性能等因素的影响,影像往往会发生色偏现象,使地物失去真实色彩。为解决这一问题,国内外学者提出了很多方法:比如魏东等[1]提出了一种基于颜色校正和去模糊的水下图像增强方法,张守权等[2]针对无人机三维重建后的纹理色差问题,提出了快速、高效的无缝纹理匀光方法。Yoon et al.[3]则提出了利用卷积稀疏编码和Retinex模型中的稀疏表示来实现影像增强。王密等[4]通过匀光处理来使影像达到色彩平衡。然而这些方法只能一定程度地保证影像整体的色彩一致性,并不能使地物完全恢复其原有色彩。
笔者针对轻小型无人机拍摄的航空影像,在对其进行匀光处理的基础上,依据近距离拍摄的参考影像,对影像进行色彩校正。并通过定性分析和定量分析,对比不匀光及Mask匀光、Wallis匀光和Retinex匀光后进行色彩校正的结果,寻找校正结果与参考影像最为接近且能还原地物真实色彩的方法。
1 影像匀光算法
在遥感影像获取过程中,由于内部或外部环境等因素的干扰,会使得一幅影像各部分色调、亮度、对比度等存在不同程度的差异,这种现象称之为不均匀光照现象[5],为消除这种现象所做的处理称为影像匀光,该方法能够为后续研究提供色彩一致、视觉效果统一的基础性数据。匀光算法大体可分为3大类[6]:①基于加性噪声模型的匀光算法(如Mask算法);②基于统计方法的匀光算法(如Wallis算法);③基于照度与反射率模型的匀光算法(如Retinex算法)。
1.1 Mask算法
Mask又称模糊正像匀光法。由于不均匀光照,在像片晒印时,负片透明处曝光量多,不透明处曝光量少。Mask算法则对二者进行补偿,获得照度均匀的影像。按照其原理,对于数字航空影像,数学模型可用式(1)进行表述。
I′(x,y)=I(x,y)+B(x,y)
(1)
式(1)中:I′(x,y)表示原始影像,I(x,y)表示光照均匀的影像,B(x,y)则表示背景影像。不均匀光照的影像被认为是光照均匀的影像叠加背景值所造成的,故而匀光的过程转换为去除背景值的过程。背景影像的模拟有多种方法,由于其亮度分布的不规则性,很难用数学模型来表示,所以普遍采用低通滤波的方法来获取代表亮度色调的低频部分,将其作为背景影像。
高斯低通滤波器具有在空间域和频率域误差最为稳定的特征,经常被选为最佳的滤波器。数学模型如式(2)所示。
(2)
式(2)中:G(x,y)为滤波器处理后获得的背景影像,x,y为像素坐标,σ为截止频率。通过高斯低通滤波器获取背景影像后,用待校正影像与背景影像做相减运算即可获得理想条件下光照均匀的影像。为使处理后的影像灰度值在0~255之内,还需要加上一个偏移值offset。同时它也决定了图像处理后的平均亮度,该值一般取原影像的亮度均值。
I(x,y) =I′(x,y)-G(x,y) + offset
(3)
为避免由相减运算造成的影像整体反差变小,还需要对图像进行拉伸,以增大整体反差。

(4)
式(4)中:I为匀光后未拉伸的影像,NI为拉伸处理之后的影像,V为拉伸系数,一般取-127~127。Mask算法虽可以较好地进行匀光处理,但很容易产生光晕现象,且对于不同的影像,其高斯低通滤波器的截止频率很难确定,只能依靠经验值对影像进行特定分析。一般的卫星遥感影像截止频率取80,本文根据实验确定轻小型无人机像片进行高斯低通滤波的截止频率为10。
1.2 Wallis算法
该算法,即运用Wallis滤波器将待校正影像的灰度均值和方差映射到给定范围内,从而让整幅影像不同位置的均值和方差趋于一致[7],其数学模型如式(5)所示:
(5)
式(5)中:I(x,y)为匀光后的影像,I′(x,y)为原始影像,mi′和si′为原始影像的均值和标准差,mf和sf为参考影像的均值和标准偏差,b、c分别为方差扩展常数与亮度系数,且b∈[0,1],c∈[0,1]。当b、c都取1的时候,便视为将mi′、si′强制归结到mf、sf,则式(5)可变为以下形式:
(6)
该方法不但可以在增强局部反差的同时大大抑制噪声,还具有较强的适应功能。但缺点是对低亮度区域的增强效果并不显著,同时还会产生“块效应”。
1.3 Retinex算法
Retinex算法是由美国E.H.Land[8]提出的一种基于照度与反射率模型的匀光算法。其主要思想是将待校正的原始影像看作是由入射光影像与反射光影像结合而成,如图1所示。

图1 Retinex算法示意图Fig.1 Retinex algorithm diagram
将入射光影像记做L(x,y),反射光影像记做R(x,y),原始影像记做I′(x,y),则Retinex算法数学模型可用式(7)表示。
I′(x,y)=L(x,y)·R(x,y)
(7)
我们将反射光影像作为物体真实情况的反映,只要能估计出入射光影像,将其消除,便能获得亮度均匀的影像。将式(7)取对数。
logR(x,y)=logI′(x,y)-logL(x,y)
(8)
且令:
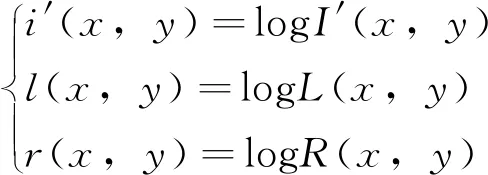
(9)
可得:
r(x,y)=i′(x,y)-l(x,y)
(10)
1.3.1 单尺度Retinex算法
入射光影像可以用高斯函数与原始影像卷积获得[9],则式(10)可变为:
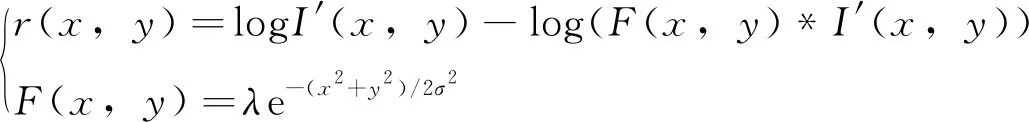
(11)
式(11)中: *表示卷积运算,F(x,y)为高斯函数模型,σ为尺度参数,对于单尺度Retinex算法,σ一般取80~100之间,并且λ需满足:
∬F(x,y)dxdy=1
(12)
单尺度算法在σ取值较小时,色彩差别较大,而当σ取值较大时,又会使图像动态压缩范围减小,从而丢失细节。为解决这一问题,又有学者提出了多尺度Retinex算法。
1.3.2 多尺度Retinex算法
多尺度Retinex (RMSR)算法[10]是将σ取大、中、小3个参数后,分别进行单尺度运算。然后再将结果进行加权平均,权值一般取1。多尺度算法相较于单尺度具有更好的动态压缩范围,还可以很好地保证图像的质量,使得图像的细节和色彩更加真实。
1.3.3 带色彩恢复的多尺度Retinex算法
对于彩色影像来说,只需对R、G、B三个通道分别进行处理后再进行合并,就可以获得处理后的彩色影像。然而R、G、B三个通道之间是存在关联性的[11],这种分离式的操作会使得影像色彩失真。为解决这一问题,Jobson et al.[12]提出带色彩恢复的多尺度Retinex(RMSRCR)算法。
该方法的基本思想即在多尺度算法的基础上增加色彩恢复的步骤,首先在多尺度运算之前计算一个色彩校正因子C。
(13)
式(13)中:N=3,代表R、G、B三个通道,Ii′(x,y)代表原始影像。然后对式(13)做对数处理
Ci(x,y)=β·log[α·Ci(x,y)]
(14)
式(14)中:α为调节参数,β为增益常数,参考以往研究[13],当α=125,β=-46时效果最好。随后将多尺度计算结果乘上色彩校正因子即可获得色彩恢复后的图像。
RMSRCRi(x,y)=Ci(x,y)·RMSRi(x,y)
(15)
式中:i表示R、G、B三个通道。
2 基于参考影像的色彩校正
基于参考影像的色彩校正方法,实际上就是通过待校正影像上定标点与参考影像定标点的灰度值之差来拟合背景值,继而消除背景值的过程。首先,应获取待校正影像上定标点的灰度值,并记录定标点的像素坐标;然后于参考影像上获取定标点的参考灰度值,取二者的差值;随后通过最小二乘拟合得到灰度差与定标点之间的多项式模型,确定背景曲面;最后代入每一个像素点的坐标值,逐个像素改正,获得校正后的影像。其中,定标点的选取至关重要。
2.1 定标点的选取
为建立适合的色彩校正模型,定标点需要均匀地分布在整张图像上,否则会产生较大的拟合误差[14]。采用“九点法”,将影像平均划分为9个区域,每个区域各取一个定标点,以充分保证定标点的均匀分布。
为拟合背景影像,需要获取原始影像和参考影像上定标点的灰度值和原始影像上定标点的坐标。对于灰度值的选取,不应单单选取一个像素点,而是挑选影像上最具代表性的且仅含有一种地物的区域,找到其R、G、B三个通道上统计量最大的值作为定标点的灰度值,以避免因地物较多所造成的灰度偏差。
对于坐标,应取所选区域内有效点的坐标均值。即在获取定标点灰度值后,设定一个阈值α(一般取20[4])。以灰度值为基准,阈值上下浮动的点都认为是有效点。记定标点灰度值为(R0,G0,B0),则有效点表示为:
(R,G,B)=(R0±α,G0±α,B0±α)
(16)
最后,定标点的坐标为。
(17)
式(17)中:(xi,yi)为有效点的坐标,n为有效点个数。
2.2 背景影像的拟合
在获取相应的定标点位置信息后,建立背景拟合模型为:
(18)
式(18)中:f(x,y)为拟合的背景影像,aij为系数矩阵,(x,y)为原始影像像素坐标。将定标点坐标与定标点在原始影像和参考影像上的灰度值之差代入方程,按最小二乘法求解出模型系数,建立数学模型。最后将原始影像上的像素坐标一一代入,求解出每一个像素的灰度改正值,达到色彩校正的目的。
I(x,y)=I′(x,y)-f(x,y)
(19)
式(19)中:I(x,y)为校正后影像,I′(x,y)为原始影像。
2.3 拼接缝的消除
为消除分块处理后合并时出现的拼接缝,本文采用羽化法[15]来减弱拼接缝对整幅影像的影响。首先在拼接缝左右取一定范围L,统计拼接缝两侧L内的灰度差Δg,再确定改正宽度W。
W=K·L
(20)
式(20)中:K为改正参数,一般取0.8~1.5[16]。确定改正宽度后,则到拼接缝距离为d的像素的改正量可表示为:
(21)
由式(21)可对改正宽度内每一个像素进行修改,最终达到消除拼接缝的目的。
3 实验流程及结果分析
3.1 实验流程
尽管对数字航空影像进行匀光处理可以一定程度地校正色彩,但是很难将地物恢复到其真实的色彩。仅通过参考影像拟合背景值[17]来进行色彩校正虽可以使地物色彩更加真实,却无法解决因光照不均匀而产生的局部色偏现象。本文采用先匀光,后校正的方法。将待校正原始影像分块,并分为R、G、B三个通道,对每一块影像的每个通道都在不匀光、Mask匀光、Wallis匀光和Retinex匀光下进行色彩校正,合并3个通道的结果获得彩色影像,合并分块处理的影像,消除拼接缝。对比分析4组实验结果,实验流程如图2所示。

图2 实验流程图Fig.2 Experimental flow chart
3.2 实验结果与分析
实验影像采用大疆精灵4A拍摄,航高120 m,相机焦距8.8 mm,像片尺寸为5 472×3 648,像元尺寸为0.002 63 mm,试验区面积约3 000 m2。
对原始影像、参考影像分别在不匀光、Mask匀光、Wallis匀光和Retinex匀光下进行色彩校正的结果如图3所示。

图3 原始影像、参考影像及其色彩校正结果Fig.3 Original image, reference image and color correction results
3.2.1 定性分析
由图3(a)、(b)可以看出,待校正原始影像相较于参考影像,色调更浅,亮度更高,树木及草地的饱和度不够,且丢失了很多纹理信息。由图3(c)-(f)可以看出,经过校正之后的影像,色调加深,亮度降低,饱和度提升,还原了部分纹理细节,相较于原始影像,更加接近地物真实色彩。其中,目视对比不匀光及3种匀光结果发现,不匀光直接进行色彩校正的结果虽整体色彩较为接近参考影像,但会产生因光照不均匀造成的局部色偏现象,拼接缝消除效果不理想;Mask匀光后校正的效果较差,会产生局部亮度过高的情况;Wallis匀光后校正的效果在4种方法中可以最好地还原地物纹理信息,石路和草地的纹理更加明显,但会出现饱和度过高的情况,使地物色彩偏离真实值;而Retinex匀光后校正结果的色调、亮度、饱和度都更贴合参考影像,同时还能保证地物的纹理信息,能较为真实地还原地物色彩,拼接缝消除效果最佳。
3.2.2 定量分析
定量分析分别采用局部定量分析和整体定量分析,局部定量分析采用色差(ΔE)[18]和直方图相似度(S)[19]对影像中4种主要地物:砖路、石路、草地和灌木分别进行评价,ΔE用来分析校正后影像与参考影像的色彩偏差,其值越小说明色彩越接近参考影像。S用来评价校正后影像与参考影像的相似程度,越接近于1则越相似。整体定量分析则采用标准差(STD)[4]和平均梯度(MG)[20]对整张影像进行评价,STD用来描述校正前后影像整体色彩真实性的恢复程度,STD越小效果越好。MG用来反映纹理细节,越接近参考影像,校正效果越好。
局部定量色差(ΔE)分析见表1,局部定量相似度(S)分析见表2。

表1 局部定量色差分析

表2 局部定量相似度分析
进一步绘制不同地物局部定量分析指标图,ΔE 、S分别见图4(a)、(b)。

图4 不同地物的ΔE、S Fig.4 ΔE and S of different ground objects
由图4(a)可以看出,经过色彩校正后影像的ΔE相较于原始影像的ΔE均有所降低,其中,Retinex匀光后校正影像的ΔE最小,4种地物的颜色最为贴合参考影像。而Mask匀光后校正和Wallis匀光后校正影像的ΔE大于不匀光校正后影像的ΔE,效果较差,且在草地、灌木等纹理复杂的自然地物上差异更加明显。
由图4(b)可以看出,校正后影像的S对于砖路、石路等纹理规则的人工地物效果更好,而对草地、灌木等纹理复杂的自然地物会产生较大偏差。Retinex匀光后校正影像的S最接近1,4种地物与参考影像最为相似。
整体定量分析结果如表3所示。

表3 整体定量分析
为进一步分析结果,计算各校正方法相对于原始影像的STD缩小百分比,以及MG偏离值缩小百分比。不同方法的STD缩小百分比及MG偏离值缩小百分比如表4所示。

表4 STD缩小百分比及MG偏离值缩小百分比
进一步绘制整体定量分析指标图, STD缩小百分比、 MG偏离值缩小百分比分别见图5(a)、 (b)。
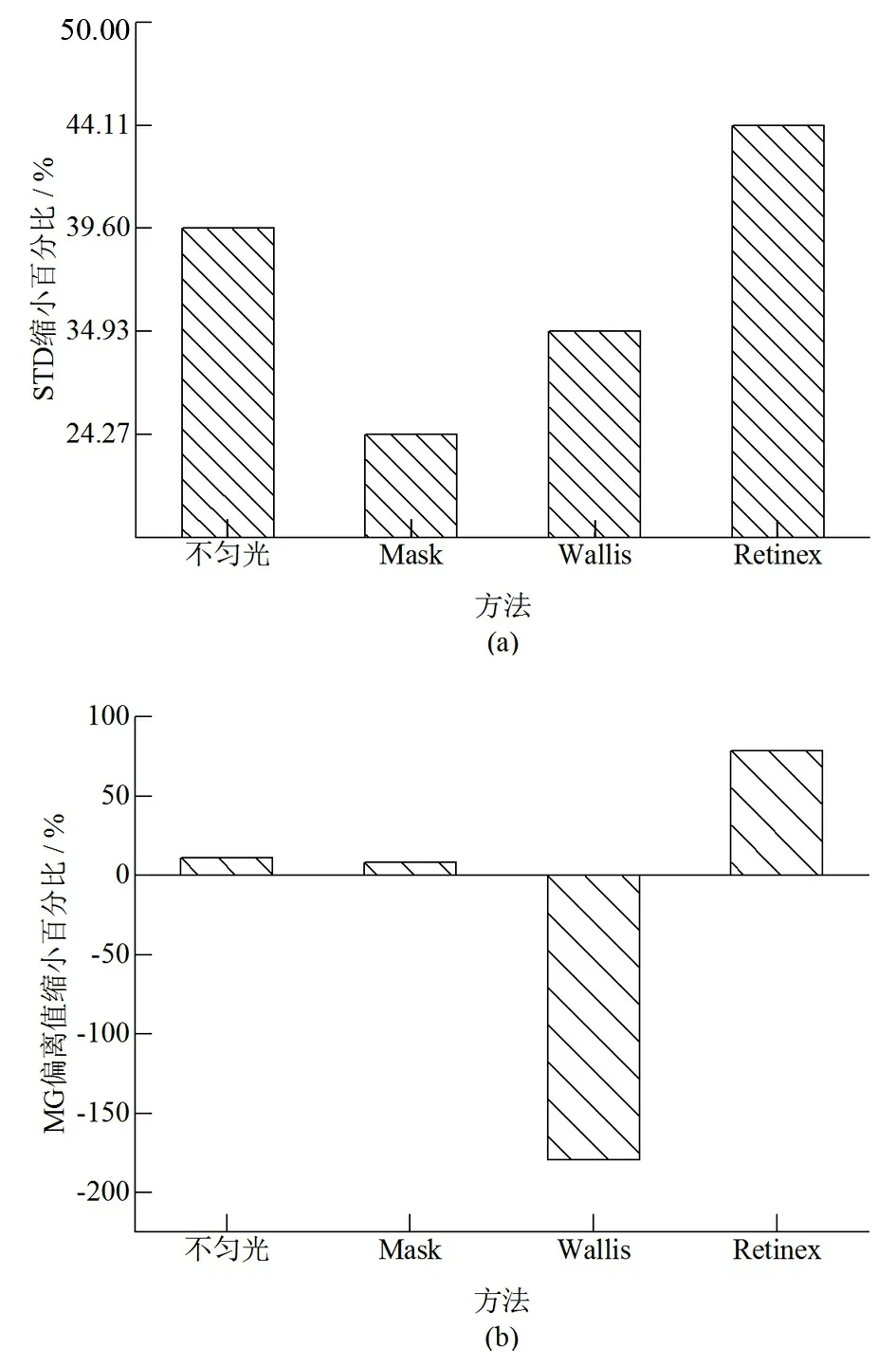
图5 不同方法的STD缩小百分比及MG偏离值缩小百分比Fig.5 STD reduction percentage and MG deviation reduction percentage of different methods
从图5(a)可以看出:Retinex匀光后校正结果的STD相较于原始影像缩小44.11%,校正效果提升最明显,而Mask匀光后校正和Wallis匀光后校正的效果相对较差,其中Mask匀光后校正结果的STD仅缩小24.27%。由图5(b)可以看出,Retinex匀光后校正结果的MG偏离值缩小78.74%,最贴近参考影像,校正效果最好,而Wallis匀光后校正结果由于纹理细节过于突出,MG偏离值缩小百分比达到 -179.41%,校正结果偏离参考影像。
4 结论
(1)基于局部定量分析,经匀光处理后再进行色彩校正的结果存在地物差异。砖路、石路等纹理规则的人工地物校正结果较好,ΔE较小,S较大,而草地、灌木等纹理复杂的自然地物则偏差较大。其中,Retinex匀光后校正的结果最为稳定,各地物亮度均一,纹理明显,对于4种地物的ΔE最小,与参考影像S最为接近,可以很好地反映地物真实色彩。而对石路、草地和灌木,Mask与Wallis匀光后校正的结果相对不匀光校正的结果较差。
(2)基于整体定量分析,Retinex匀光后校正结果相较于原始影像,标准差和平均梯度偏离值分别缩小44.11% 和 78.74%,最贴近参考影像,色彩也更接近真实地物,而Mask与Wallis匀光后校正的结果偏离参考影像,其中Wallis匀光后校正结果的地物纹理最为突出,产生色调过饱和现象,偏离真实地物。Retinex匀光后的色彩校正取得了较好的色彩校正结果,有利于航空影像的建模、解译等工作。
