SPM和GVD对单模光纤中传输的超高斯脉冲的影响

蔡 培 君

(安徽大学江淮学院 理工部, 安徽 合肥 230039)

光脉冲在单模光纤中传输时,由于群速度色散(GVD)和自相位调制(SPM)等非线性效应的影响,使得光脉冲的频率随时间变化,产生频率啁啾,使得脉冲波形发生畸变,且随着输入光脉冲功率的增加,其受到的非线性效应的影响将进一步增强[1]。超高斯脉冲相对于高斯脉冲来说有更加陡峭的前沿和后沿,且可以直接通过调制激光器实现输出,因此超高斯脉冲在现代光通信中有很重要的应用价值,对超高斯脉冲在光纤中的传输特性的研究有重要意义[2-4]。本文以非线性薛定谔方程为基础,利用分步傅里叶法,通过数值模拟,对超高斯脉冲在单模光纤中的传输特性进行研究,分析了GVD和初始啁啾对超高斯脉冲传输的影响。

1 基本理论

设脉冲的瞬时频率为时间t的函数,则其瞬时频率可以表示为

ω(t)=ω0+δω(t)。

(1)

式中:ω0为不考虑非线性效应时的载波频率;δω(t)是由非线性效应引起的频率的变化量。因此δω(t)可以看作瞬时频率和载波频率的差,且随时间t的变化而变化,称为频率啁啾量[5-8]。正是由于频率啁啾量的存在,使得光脉冲在不同时刻的瞬时频率不同,形成啁啾脉冲。

δω(t)随时间的变化率记为C,C称为啁啾参量或称为啁啾系数。当C>0时,称为正(或上)啁啾,即脉冲的瞬时频率随时间的增加而增加;当C<0时,称为负(或下)啁啾,即脉冲的瞬时频率随时间的增加而减小;当C=0时,脉冲无啁啾,即脉冲的瞬时频率不随时间变化而变化,为一常量。不同啁啾系数下脉冲瞬时频率变化如图1所示。

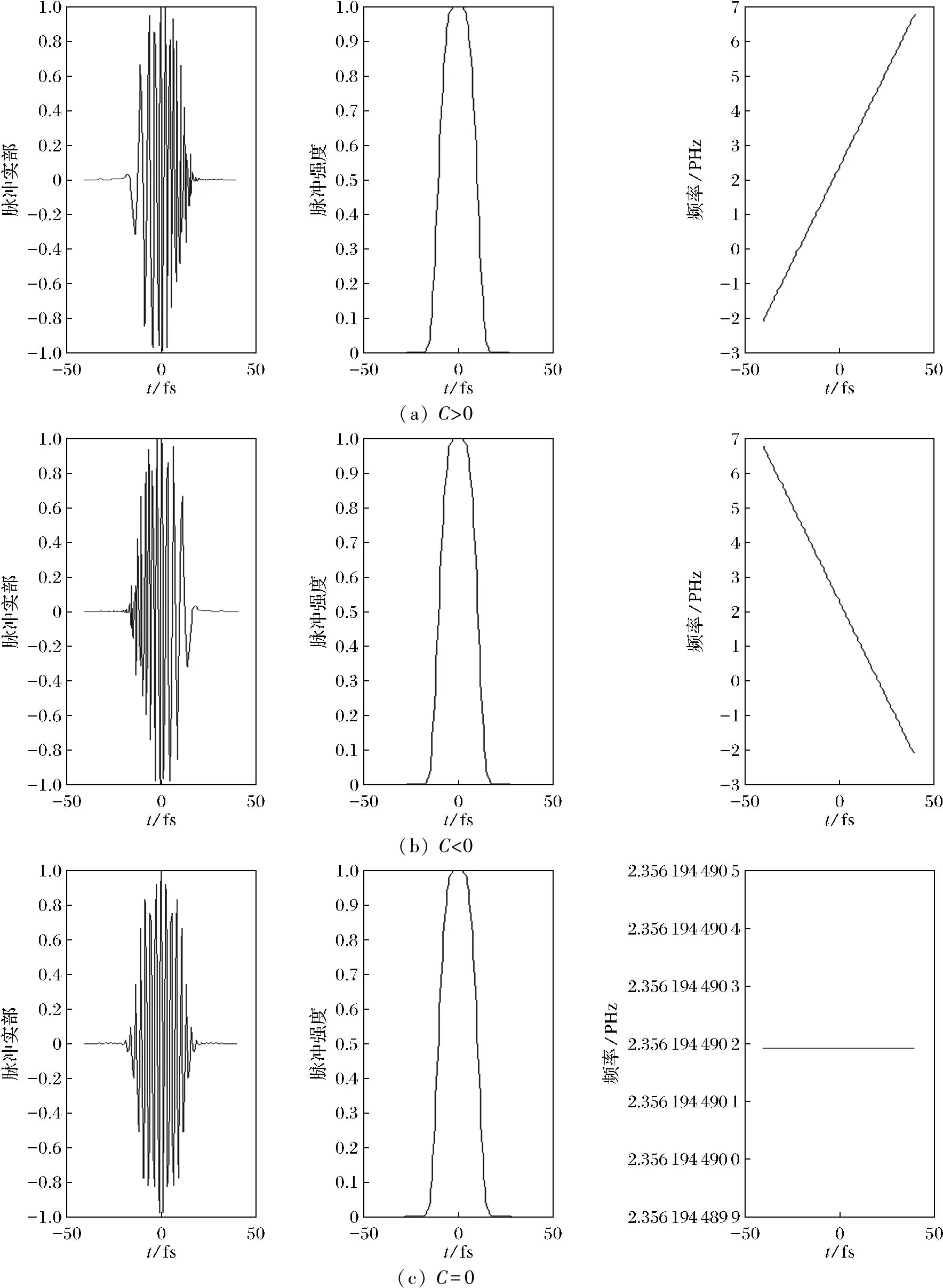
(a) C>0(b) C<0(c) C=0

2 基本传输模型

单模光纤中光脉冲满足的非线性传输方程如式(1)所示。

(2)

式中:A为脉冲包络的慢变振幅;z为传输距离;T为脉冲以群速度vg移动为参考坐标系中的时间参量,T=t-z/vg;α为光纤的衰减系数;β2为光纤的二阶色散系数;β3为光纤的三阶色散系数;γ为光纤的非线性系数;i为虚数单位。式中第3项表示光脉冲在光纤中传输时的群速度色散,第4项表示光脉冲在光纤中传输时的自相位调制[9-10]。

引入归一化振幅U,设

(3)

式中,P0为入射脉冲的峰值功率。则式(2)可改写为

(4)

光脉冲在单模光纤中传输时,会同时受到色散和非线性作用的影响,根据分步傅里叶法,式(4)可以改写为

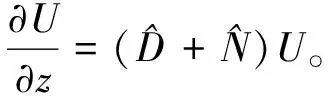
(5)

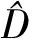
当光脉冲U(z,T)在光纤中从z处传输到z+d处后,可以得到其传输表达式如式(6)所示。

(6)

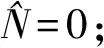
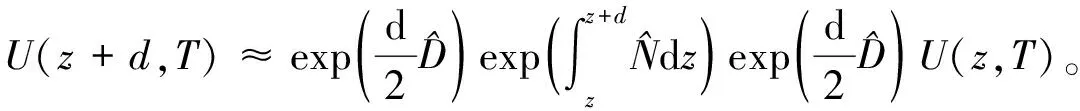
(7)

利用傅里叶变换关系及其微分关系,将色散算符在时域中的微分关系变换为频域中的乘积,即

2.2.3 管理情况 很多中职教师认为，授课内容比较重要，对学生违反课堂秩序的行为不加以制止，使其变本加厉；有些教师温和胆小，上课时不看学生，不了解学生的接受能力，难免会出现课堂问题行为；有些教师处理不当，会将小问题变成大问题；还有些教师喜欢训斥、威胁甚至恐吓学生，容易引起学生的逆反情绪和课堂问题行为。

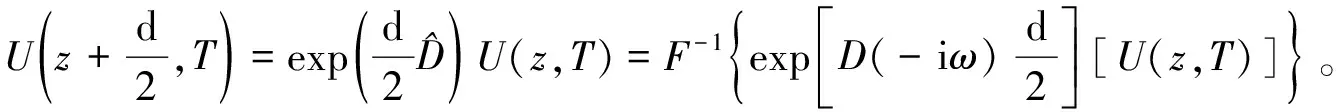
(8)

式中:F表示傅里叶变换;F-1表示傅里叶反变换。

2.1 自相位调制引起的脉冲波形的演变

假设无初始啁啾,即C=0,当光纤长度L≪LD,且L≈LNL时,GVD作用可以忽略,仅考虑自相位调制对超高斯脉冲传输波形的影响。入射光场为如式(9)所示的超高斯脉冲。

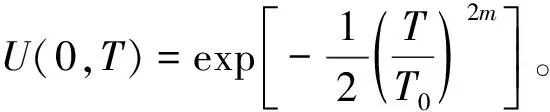
(9)

此时式(4)可化简为

(10)

式中:LNL为单模光纤的非线性长度;LNL=1/γP0。可得式(10)的解为

U(z,T)=U(0,T)eiφNL(z,T),

(11)

则根据式(10)和式(11)可以得到在单模光纤中传输的超高斯脉冲的非线性相移φNL(z,T)和频率的变化量δω(T)为

式中,zeff为光纤的有效长度,zeff=(1-e-αz)/α。

根据式(12)可以发现,在单模光纤中传输的超高斯脉冲,随着传输距离的增加,使得脉冲的相位发生变化,即发生了非线性相移,且非线性相移随着光纤的有效长度的增加而增加,但脉冲波形不变。如图2(a)所示(见封2)。根据式(13)分析可得,SPM使得在单模光纤中传输的超高斯脉冲产生了频率啁啾。但由SPM引起的频率啁啾仅发生在超高斯脉冲的前后沿附近,呈非线性变化,这一点与高斯脉冲不同,如图2(b)所示(见封2)。

若超高斯脉冲含有线性初始源啁啾,即C≠0,且光纤长度满足L≪LD,且L≈LNL,仅考虑SPM对脉冲传输的影响,此时入射光场为如式(14)所示的超高斯脉冲。

(14)

带入式(10)求得任意位置脉冲振幅为

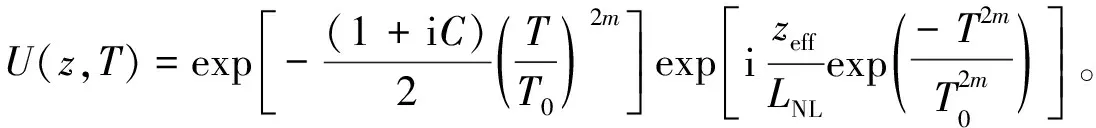
(15)

则随着传输距离的增加产生的非线性相移φNL(z,T)和频率的变化量δω(T)为

分析式(16)和(17)可以发现,SPM引起的频率啁啾与初始源啁啾有关。在传输过程中超高斯脉冲的相位也受到初始啁啾的影响。

2.2 群速度色散(GVD)引起的脉冲波形演变

假设无初始啁啾,即C=0,当光纤长度L≪LNL,且L≈LD时,此时非线性效应的影响可以忽略,仅考虑GVD对脉冲的影响,则可以对式(4)进行化简,如式(18)所示。

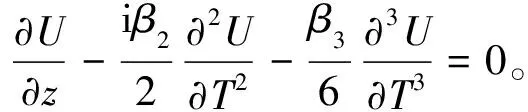
(18)

利用傅里叶反变换可以求得式(18)的解为

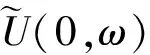
(20)

当超高斯脉冲无初始源啁啾,即C=0时,取β2=10 ps2·km-1,β3=0。当m在2～5变化时,脉冲在单模光纤中传输的波形演变如图3(a)所示(见封2)。

由图3中的脉冲波形演变曲线可以看出,在光脉冲无初始啁啾情况下,随着其在单模光纤中传播距离的增加,由于群速度色散的影响,超高斯脉冲经历了平顶→多峰→单峰的演变过程,脉冲宽度不断增加,脉冲峰值先增加后减小,且在脉冲的前后沿出现了振荡拖尾。随着m的增大,脉冲最大峰值增大,脉冲前后沿拖尾增长,且振荡加剧。而这种脉冲宽度的增加正是由于不同频率分量在光纤中传播的速度不同造成的,即超高斯脉冲经过单模光纤传输后出现了频率啁啾。

取m=2时,二阶色散系数取β2=10 ps2·km-1,当啁啾系数C分别取2、4、8、12时,超高斯脉冲在单模光纤中传输的波形演变如图4所示(见封3)。

通过观察图4可以发现,相对于无初始啁啾的超高斯脉冲来说,初始正啁啾的存在使得入射的超高斯脉冲在单模光纤中传输时波形演变速度更快,并且随着初始啁啾的增大,波形变化越剧烈,初始正啁啾增强了群速度色散对脉冲波形的影响。

取m=2时,二阶色散系数取β2=10 ps2·km-1,当啁啾系数C分别取-2、-4、-8、-12时,超高斯脉冲在单模光纤中传输的波形演变如图5所示(见封3)。

通过观察图5可以发现,相对于初始正啁啾的超高斯脉冲来说,初始负啁啾的存在使得入射的超高斯脉冲在单模光纤中传输时,脉冲时域波形并没有迅速展宽,而是一个先变窄再展宽的过程,初始负啁啾抵消了一部分GVD对脉冲波形展宽的影响,但随着传输距离的增加,GVD对脉冲波形展宽的作用愈加明显。

3 结 论

本文以非线性薛定谔方程为基础,利用傅里叶变化法,分别讨论了SPM和GVD对单模光纤中传输的超高斯脉冲的影响。通过数值模拟,对超高斯脉冲在单模光纤中的传输特性进行仿真,分析了SPM、GVD以及初始啁啾对超高斯脉冲波形的影响。分析结果表明,随着传输距离的增加,单模光纤的SPM和GVD效应都能引起其中传输的无源啁啾超高斯脉冲频率啁啾,频率啁啾量与超高斯脉冲的阶数有关。SPM引起的频率啁啾仅发生在脉冲沿附近,在脉冲前沿附近为负(红移),在脉冲后沿附近为正(蓝移),呈非线性变化。同时超高斯脉冲的初始源啁啾的大小对其传输过程中产生的频率啁啾也有影响。