竖直振动激励下颗粒毛细上升行为研究*
2022-06-04于天林凡凤仙2
于天林 凡凤仙2)†
1) (上海理工大学能源与动力工程学院,上海 200093)
2) (上海理工大学上海市动力工程多相流动与传热重点实验室,上海 200093)
竖直振动激励下颗粒毛细上升现象为颗粒物料的提升、输运和采集提供了一种全新的技术路径.然而,已有颗粒毛细上升行为研究仍存在明显不足,特别是缺乏对重力加速度、水平振动分量、颗粒粒径分布影响的深入探究.针对这些问题,采用离散元方法,对不同操作条件下颗粒毛细上升现象开展数值模拟研究,并对颗粒最终毛细上升高度和平均毛细上升速度进行计算分析.结果表明,在低重力条件下,颗粒毛细效应仍能发生,颗粒最终毛细上升高度和平均毛细上升速度随重力加速度均呈现先增加后减小的趋势;颗粒最终毛细上升高度对水平振动分量的变化不敏感,而平均毛细上升速度随水平振动分量的增大而增加;在平均粒径相等的情况下,粒径服从高斯分布的颗粒比单一粒径颗粒的最终毛细上升高度最大值对应的临界管径更大,并且同处于堵塞效应影响的管径区域时平均毛细上升速度也更快.
1 引言
颗粒物质是指粒径大于1 µm 的大量离散固体颗粒组成的宏观复杂体系,其具有对外界微小作用的敏感性、非线性响应和自组织行为等[1,2].特别是,竖直振动激励下颗粒物质能够表现出复杂而奇特的动力学行为,例如:竖直振动颗粒床中颗粒的隆起和对流[3-5];竖直振动U 形分割容器或U 形管中颗粒由一侧向另一侧的迁移[6-8];竖直振动激励插入静止颗粒床中的细管时颗粒毛细上升行为[9-11]等.这些行为难以通过传统的流体力学、固体力学以及凝聚态物理理论进行解释,因而成为当前工程热物理、离散相动力学、凝聚态物理等多学科交叉的前沿领域和研究热点.
对插入静止颗粒床中的细管施加竖直方向正弦振动激励作用,在一定的振动强度下,颗粒在管内逆重力上升,并最终形成一个稳定颗粒柱高度,鉴于这一现象与与液体的毛细效应类似,被称为颗粒毛细效应[11].该现象为颗粒物料的提升、输运和采集提供了一种全新思路,具有工程应用的潜力,因而备受关注.近年来,一些学者对此开展了一系列实验观测、理论分析和离散元模拟研究,探讨了振动条件、几何参数、颗粒粒径对颗粒毛细上升高度和速度的影响[9-23],分析了颗粒毛细上升的“空穴填充”机理[21],发现了颗粒毛细上升的内在物理机制—颗粒对流[11-14],提出了颗粒毛细上升高度的理论模型[23]等.
然而,由于颗粒毛细上升过程机理复杂、影响因素繁多,在颗粒毛细上升行为研究方面仍存在明显不足.首先,已有研究集中在开展地面实验或在地面重力加速度下开展数值模拟,考察无量纲振动强度(最大振动加速度与重力加速度的比值)对颗粒毛细上升的影响规律,低重力条件下颗粒毛细效应的文献报道仅见Kawamoto 等[20]在重力加速度g=1.6 m/s2情况下数值模拟得到的颗粒毛细上升高度随时间的演变,尚缺少颗粒毛细上升行为受重力加速度影响的深入探究.其次,实际的竖直振动系统中,由于扰动的存在,微小的水平振动分量难以避免,已有对竖直振动U 形管中颗粒迁移行为的研究表明,水平振动分量的存在有利于颗粒由一个分支向另一个分支的迁移[8],然而水平振动分量对颗粒毛细上升行为的影响特性尚未被研究.再者,已有颗粒毛细上升行为研究采用的颗粒均为单分散颗粒,多分散颗粒的毛细上升行为有待研究.
鉴于已有研究中存在的上述问题,本文基于离散元方法,对竖直振动激励下颗粒毛细上升行为开展数值模拟,对比分析低重力与地面重力条件下颗粒毛细上升过程,揭示颗粒最终毛细上升高度与平均毛细上升速度随重力加速度、水平振动分量的变化规律,考察粒径分布对颗粒毛细上升动力学的影响特性,以期为振动体系下颗粒的动力学行为研究提供参考.
2 离散元模型与数值计算方法
2.1 离散元模型
离散元模型的基本思想是:将颗粒物质视为离散颗粒的集合体,每个离散颗粒的运动都服从牛顿第二定律,通过求解各颗粒的运动过程,获得颗粒系统的整体行为规律.针对颗粒毛细上升行为发生的系统,考虑颗粒间接触力、颗粒受到的重力、切向接触力产生的力矩和滚动摩擦力产生的力矩,建立描述颗粒运动的离散元模型.颗粒系统中任意颗粒i的运动方程可写为:

式中,mi为颗粒i的质量,vi为颗粒i的速度,t为时间,N为与颗粒i相接触颗粒的数目,Fn,ij为与颗粒i相接触的颗粒j对颗粒i的法向作用力,Ft,ij为颗粒j对颗粒i的切向作用力,g为重力加速度,Ii为颗粒i的转动惯量,ωi为颗粒i的角速度,Mt,ij为颗粒j对颗粒i的切向作用力产生的力矩,Mr,ij为颗粒j对颗粒i的滚动摩擦力产生的力矩.
分别采用黏弹性接触模型与修正的Cundall-Strack 模型计算颗粒间的法向作用力[24]与切向作用力[25],依据定量恒转矩模型计算滚动摩擦力产生的力矩[26],接触力和力矩的表达式详见文献[12,13],此处不再赘述.在本文所考虑的颗粒系统中,除了颗粒间相互作用外,还存在颗粒与容器壁及管壁的相互作用.对于颗粒i与壁面的相互作用,将壁面视为半径无限大的颗粒处理.
2.2 数值计算方法
基于上述离散元模型,借助开源颗粒系统数值模拟软件LIGGGHTS[27]对竖直振动激励下颗粒毛细上升行为开展数值模拟研究.图1 给出了数值模拟采用的颗粒系统示意图.如图所示,内径为D的圆柱形容器中填充有大量颗粒,将内径为d、壁厚为δ的圆管沿容器的中心轴线竖直插入颗粒层,直至管底面与容器底面的距离为L.其中,颗粒层利用数值模拟方法生成,具体过程为:在容器内(包括管外和管内区域)随机加入初速度为0 的模拟颗粒,使颗粒遵循(1)式、(2)式给出的运动方程发生沉降运动,颗粒系统的总动能先增大后减小,并最终形成总动能为0 的堆积状态.
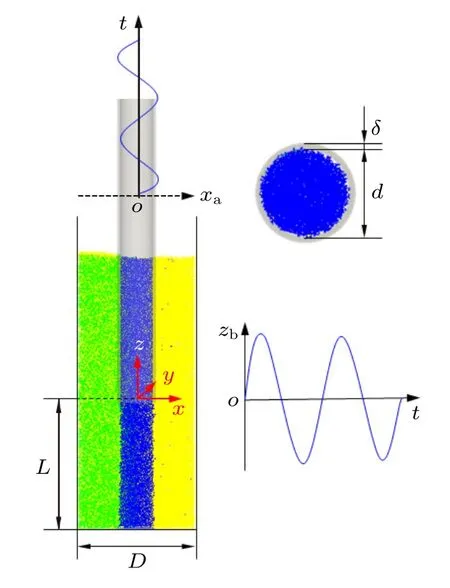
图1 颗粒系统示意图Fig.1.Schematic diagram of granular system.
以管的底面中心为坐标原点,建立三维坐标系.沿竖直方向(z向)对管施加振幅为Az、频率为f的正弦振动,则管底面的位置坐标zb随时间t的变化可写为

当考察水平振动分量对颗粒毛细上升动力学行为的影响时,除上述竖直振动外,还考虑了振幅为Ax、频率为f的水平方向(x向)正弦振动.由于该水平振动,管中心轴线的位置坐标xa随时间t的变化可写为
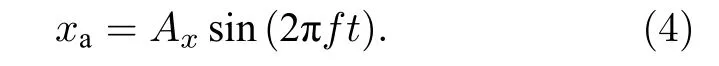
在计算模型和颗粒系统确定的情况下,离散元模拟的准确性与经济性主要受时间步长的影响.为确定时间步长,首先利用无阻尼、无黏性碰撞时间估算颗粒接触时间,即[28]

式中,meff=mimj/(mi+mj)为碰撞颗粒对i和j的有效质量,vimp为颗粒碰撞速度;ρ为弹性参数,其可表示为
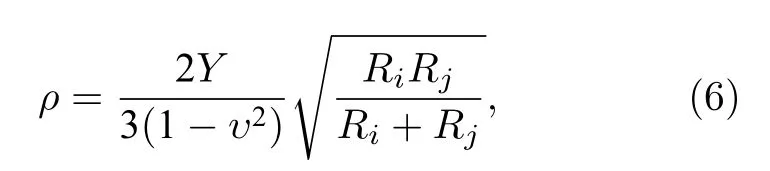
式中,Y为杨氏模量,υ为泊松比,Ri与Rj分别为颗粒i与j的半径.
数值模拟采用的参数见表1.在颗粒直径dp=0.6 mm 条件下,取vimp=1 m/s 作为颗粒碰撞速度的参考值,结合表1 给出的颗粒物性参数,计算得到tc≈ 6×10—5s.因此,选取时间步长Δt=tc/30 ≈ 2×10—6s[29,30].研究发现,若采用更小的时间步长,计算结果不发生改变,这表明时间步长的选择是合理的.此外,在该时间步长下,每计算2500 步保存一次计算结果,即一个振动周期T(T=1/f)内以等时间间隔保存20 次计算结果.
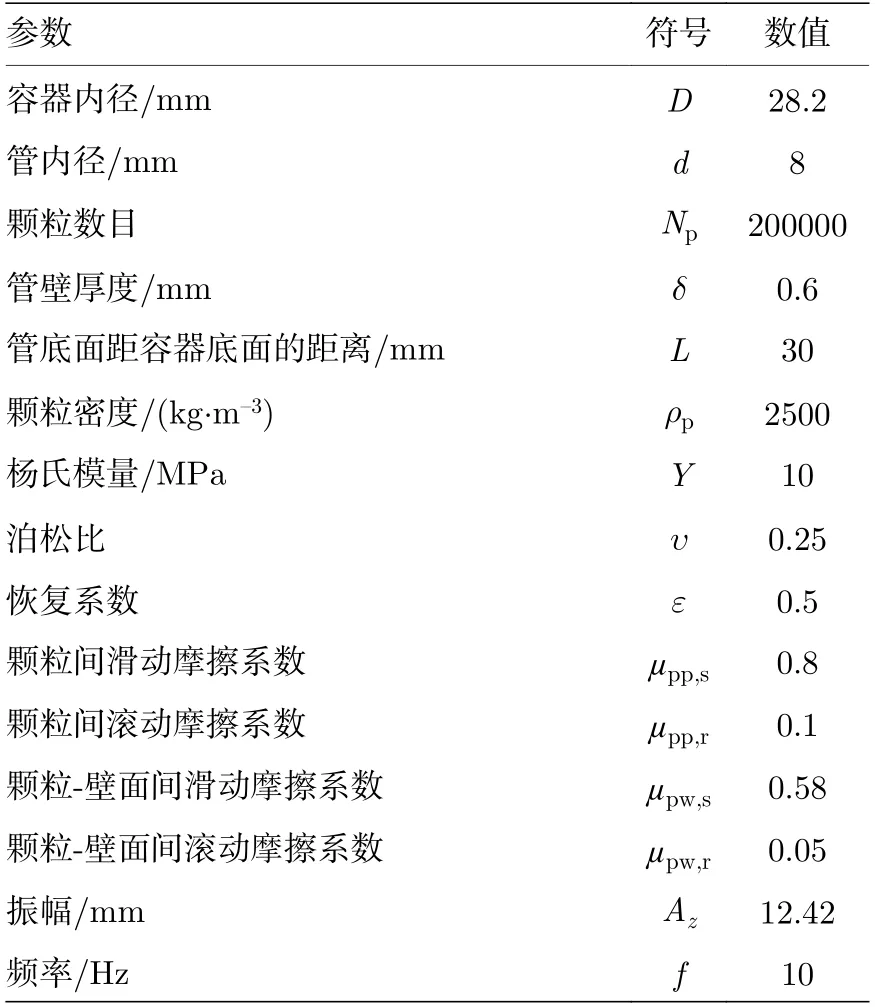
表1 数值模拟参数Table 1.Parameters used in numerical simulations.
3 结果与讨论
3.1 不同重力加速度下颗粒毛细上升行为
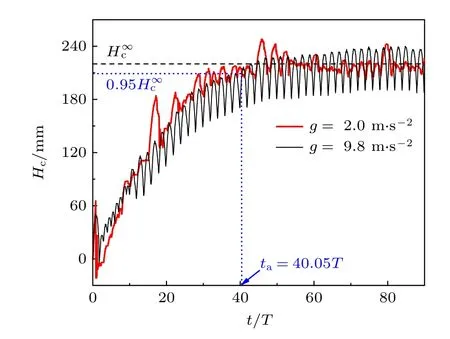
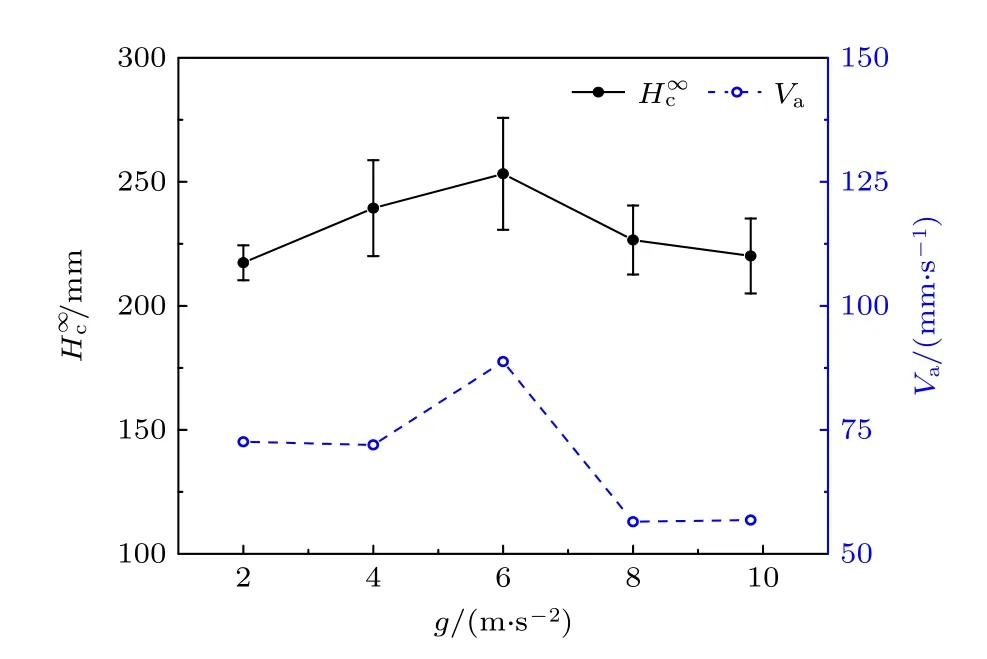
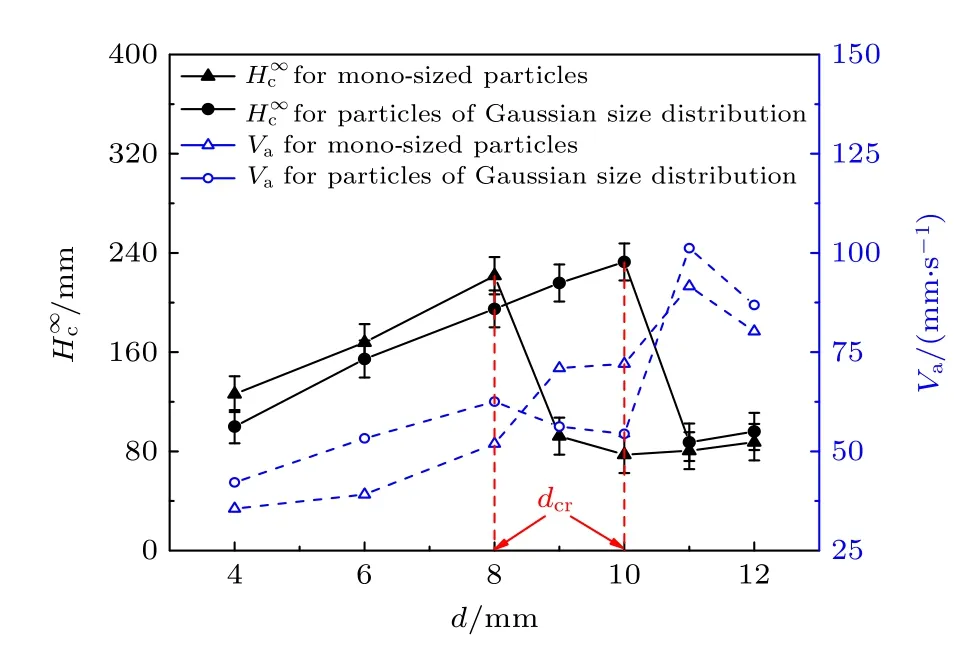
在不考虑水平振动分量(Ax=0)情况下,采用表1 给出的参数,针对直径dp=0.6 mm 的单一粒径颗粒开展数值模拟研究,考察重力加速度在2.0—9.8 m/s2范围变化时颗粒的毛细上升过程.图2 给出了重力加速度g=2.0 m/s2和g=9.8 m/s2时颗粒毛细上升动态过程的对比情况.图中,依据施加振动时刻(t=0 时)颗粒的位置对颗粒进行着色,位置矢量r满足|r| 图2 不同重力加速度下颗粒毛细上升动力学过程Fig.2.Dynamic process of granular capillary rising under different gravitational accelerations. 为定量表征颗粒毛细上升现象,引入毛细上升高度Hc、最终毛细上升高度和平均毛细上升速度Va三个参数.颗粒毛细上升高度定义为管内颗粒柱高度,即管内、管外(容器内)颗粒表面高度之差.获得Hc的方法为:将管内z> 0 的区域沿z向划分为高度Δz=5dp的连续单元,计算各单元内颗粒的填充率φ,将满足φ(z) > 0.1 的单元的最大高度作为管内颗粒表面高度zin;类似地,将容器内z> 0 且|r| >d/2 的区域沿z向划分为Δz=dp的连续单元,采用与确定管内颗粒表面高度相同的方法,获得管外颗粒表面高度zout,基于此,Hc=zin—zout.鉴于管内颗粒柱高度随着管的振动而发生周期性波动,取该阶段10T时间内Hc的平均值作为颗粒最终毛细上升高度,考虑到2.2 节给出的计算结果保存情况,则有 式中,t1为稳定阶段的起始时间,tk=t1+(k-1)T/20. 鉴于颗粒毛细效应动力学过程中由上升阶段过渡到稳定阶段是一个颗粒柱高度增加速度缓慢衰减的过程,给准确确定上升时间带来困难.为解决这一问题,选取毛细上升高度首次达到0.95 倍最终上升高度(0.95)的时刻作为上升阶段的截止时刻,用ta表示,如图3 所示,则平均毛细上升速度的表达式为 图3 毛细上升高度随时间的演变Fig.3.Evolution of capillary rising height with time. 图3 给出了g=2.0 m/s2,9.8 m/s2时颗粒毛细上升高度随时间的演变情况.总体上来说,颗粒毛细上升高度均呈现出先迅速增大,而后增速降低,直到增速约为0 时颗粒毛细上升高度达到稳定的变化趋势.然而,颗粒毛细上升高度随时间演变的细节信息有所区别.低重力条件下,颗粒毛细上升高度存在幅度不一的起伏,且这种起伏没有明显的周期性;而地面重力下,颗粒毛细上升高度随管的振动发生周期性波动,除去受初始效应影响的起始段(t=0—2T),该波动先与管的振动同频(t=2T—10T),而后频率减半(t> 10T),同时波动幅度显著增加.这是因为:低重力条件下,管内颗粒堆积疏松(见图2(a)),以至某些时段管内颗粒柱上部存在填充率φ<0.1 的稀疏区域,无法纳入颗粒柱高度,导致颗粒毛细上升高度随时间的演变呈现无序性;而地面重力条件下,管内颗粒堆积致密,除管内颗粒柱上部个别颗粒外,其余颗粒被纳入颗粒柱高度的计算范围,从而管内颗粒在管壁的周期性剪切作用下发生上升和下降运动,引起毛细上升高度发生周期性波动,此外在颗粒毛细上升过程中,颗粒间、颗粒与壁面间的碰撞和摩擦作用引起管内颗粒的填充率分布和堆积结构的改变,影响了颗粒的自组织行为,使得颗粒毛细上升高度波动呈现与管同频向频率减半转变的现象. 图4 给出了颗粒最终毛细上升高度与平均毛细上升速度随重力加速度的变化关系.图中,误差条表示颗粒最终毛细上升高度的标准差.由图可见,重力加速度在2.0—9.8 m/s2范围内变化时,颗粒最终毛细上升高度和平均毛细上升速度均呈现出先增加后减小的趋势,并均在g=6 m/s2时达到极大值,此时,=253.2 mm、Va=88.8 mm/s.Liu 和Zhao[21]根据振动输入的能量与颗粒柱的重力势能之间的平衡关系,推导出最终毛细上升高度与重力加速度及颗粒填充率负相关,而与能量输入系数(颗粒柱获得的能量与管振动动能之比)正相关.在重力加速度较小时,重力加速度增加,使得填充率增加,管内颗粒与管壁的作用增强,极大地促进了能量输入系数的增加,颗粒最终毛细上升高度增加.在重力加速度较大时,填充率和能量输入系数受重力加速度的影响均很小,因而随着重力加速度增加,颗粒最终毛细上升高度降低.综上所述,颗粒最终毛细上升高度呈现出随重力加速度的增加而先增大后减小的趋势.此外,管向上运动时,管内颗粒在管壁向上的剪切力作用下克服重力上升,在管底留下一个空穴,该空穴被容器内颗粒对流输运的颗粒所填充;当管达到最大高度转而向下运动时,颗粒在管壁向下的剪切力和重力的共同作用下减速上升,当颗粒速度减小至0 后,开始向下做加速运动,由于管内颗粒与容器内颗粒的碰撞引起的能量耗散,管内颗粒速度迅速减小为0;在管继续运动至最低位置的过程中,填充到空穴的颗粒进入管内,并在管向上加速运动时受壁面剪切力作用而上升.重力加速度较低时,容器内颗粒的对流速度较小,不利于颗粒由容器内向管内的输运;重力加速度较高时,管内颗粒重力较大,不利于填充到空穴的颗粒在管内的上升运动.因此,在管的振幅和频率不变时,存在一个使颗粒平均毛细上升速度最大的重力加速度值.此外,由于重力加速度很低时,管向上加速运动时管内颗粒极易被提升至很高的位置,而在管向下加速运动时这些颗粒难以发生重力沉降,导致管内颗粒无法形成连续的颗粒柱,因而本文对于极低重力加速度(g<1 m/s2)下颗粒的毛细上升行为未进行探讨.需要注意的是,鉴于空气的存在并非是颗粒毛细上升的决定因素,本文的数值模拟中没有考虑空气的影响.张富翁等[10]在接近真空(—95 kPa)下和常压下分别实验观测了平均粒径为 0.3 mm的颗粒的毛细上升现象,发现接近真空下颗粒最终毛细上升高度比常压下有所降低,二者之间的差在7%—13%范围内.在今后的研究中,为精确模拟颗粒毛细上升动力学行为,需要在建模时考虑颗粒与空气间的相互作用. 图4 最终毛细上升高度和平均毛细上升速度随重力加速度的变化Fig.4.Dependence of final capillary rising height and average capillary rising velocity on gravitational acceleration. 在竖直振动的基础上引入不同振幅的水平振动,在地面重力加速度(g=9.8 m/s2)条件下,针对直径dp=0.6 mm 的单一粒径颗粒毛细上升行为开展数值模拟.图5 给出了颗粒最终毛细上升高度与平均毛细上升速度随水平振动分量的变化特性.由图可知,颗粒最终毛细上升高度对水平振动振幅的变化并不敏感,而颗粒平均毛细上升速度随水平振动振幅的增大而升高.前者的原因是颗粒最终毛细上升高度由管内颗粒柱的重力势能与管的振动输入到颗粒柱的动能平衡关系决定,而地面重力加速度下,管内颗粒堆积密集,水平振动对颗粒柱动能输入的影响较小,使得颗粒柱高度变化较小.后者与Sánchez 等[8]发现的竖直振动U 形管中颗粒迁移运动的规律类似.Sánchez 等[8]实验研究发现,存在水平振动时,颗粒物质由U 形管一个分支向另一个分支迁移的速度随着水平振动分量的增大而升高,但没有对其原因进行解释.颗粒柱上升阶段管底区域颗粒平均填充率的计算结果表明,随着水平振幅的增加,颗粒填充率趋于下降.基于此,图5 所示的平均毛细上升速度变化规律可理解为:水平振动振幅的增加使得管口附近颗粒堆积更为松散,有利于容器内颗粒的对流运动,使得输运到容器中心区域,进而进入管内的颗粒质量流率增大,颗粒平均毛细上升速度增加. 图5 最终毛细上升高度和平均毛细上升速度随水平振动分量的变化Fig.5.Dependence of final capillary rising height and average capillary rising velocity on horizontal vibrational component. 在仅有竖直振动(Ax=0)时,对地面重力加速度下粒径服从高斯分布的颗粒的毛细上升行为开展数值模拟,并将数值模拟结果与平均粒径相等的单一粒径颗粒的毛细上升行为进行对比分析.高斯分布函数可写为 式中,p为频率密度,其是颗粒直径dp的函数;和σ分别为颗粒直径的平均值和标准差.模拟中采用=0.6 mm,σ=0.1. 图6 给出了两种粒径分布情况下颗粒最终毛细上升高度和平均毛细上升速度随管径的变化规律.由图可见,两种粒径分布情况下颗粒最终毛细上升高度均随管径的变化呈现先增大后急剧减小的趋势,因而存在一个使得颗粒最终毛细上升高度达到最大值的管径,这与张华腾等[12]采用方形横截面容器得到的结果定性一致.由图还可知,与单一粒径颗粒相比,高斯粒径分布条件下颗粒最终毛细上升高度最大值及其对应的管径值均较大.为表述方便,将颗粒最终毛细上升高度最大值对应的管径称为临界管径,并用dcr表示,可见两种粒径分布下dcr分别为8 mm 和10 mm.分析可知,当d≤dcr时,管内颗粒的动力学行为受到堵塞效应的影响,随着管径的增加,堵塞效应减弱,有利于颗粒的上升运动,使得此管径段内最终毛细上升高度随管径的增加而增大;当d>dcr时,堵塞效应的影响消失,管内颗粒达到流态化,颗粒呈现出液体的行为,使得此管径段内最终毛细上升高度呈现出与d≤dcr时不同的规律.本文重在关注颗粒粒径分布对毛细效应动力学行为的影响,采用的管径范围有限,然而前期研究已充分说明,当d>dcr时,颗粒最终毛细上升高度随管径的增大而趋于减小,这与液体的毛细效应一致[11,12].由于颗粒毛细效应动力学的控制机制的变化,导致在管径超过临界管径时颗粒最终毛细上升高度急剧下降.基于上述分析,高斯粒径分布下,受振动的影响,粒径较小的颗粒填充到大颗粒间的空隙中,使得管内颗粒柱的堆积密度高,阻碍了颗粒的流化,导致堵塞效应能够在更大的管径范围内影响颗粒毛细上升行为,因而高斯粒径分布下的临界管径更大.图中结果还表明,当d≤ 8 mm 时,相同管径条件下粒径服从高斯分布的颗粒最终毛细上升高度较低,但平均毛细上升速度较大.前者是因为服从高斯粒径分布的颗粒在管内的运动受堵塞效应的影响更大所致,后者则是由于堵塞效应使得颗粒毛细上升高度在更短的时间内达到稳定所致.当管径d=9 mm 与d=10 mm 时,高斯粒径分布下颗粒的平均毛细上升速度较小,这是由于颗粒毛细上升受控于不同的机制引起的.当d=11 mm 与d=12 mm 时,两种粒径分布下颗粒毛细上升动力学行为均受控于颗粒流化,使得颗粒平均毛细上升速度差异很小.竖直振动激励下粒径服从高斯分布的颗粒比单一粒径颗粒能够在更大的管径下提升到更高的高度,对于颗粒物料的提升、输运和采集具有重要意义,后续可以开展不同标准差下高斯分布颗粒以及其他粒径分布下颗粒毛细上升动力学行为研究,为颗粒毛细效应动力学行为的应用提供依据. 图6 不同粒径分布下最终毛细上升高度和平均毛细上升速度随管径的变化Fig.6.Dependence of final capillary rising height and average capillary rising velocity on tube diameter under different particle size distribution. 基于离散元方法对竖直振动激励下颗粒毛细上升行为进行数值模拟研究,获得了不同重力加速度条件下的颗粒毛细上升过程,揭示了颗粒最终毛细上升高度和平均毛细上升速度受重力加速度、水平振动分量和颗粒粒径分布的影响规律.通过研究,得到以下结论: 1) 在低重力条件下,颗粒毛细效应仍能发生;随着重力加速度的增加,最终毛细上升高度和平均毛细上升速度均呈现先增大后减小的变化趋势,在重力加速度为6 m·s—2时达到极大值. 2) 最终毛细上升高度对水平振动分量不敏感,但平均毛细上升速度随水平振动分量的增大而增加. 3) 粒径服从高斯分布的颗粒与平均粒径相等的单一粒径颗粒相比,最终毛细上升高度最大值对应的临界管径更大,并且同处于堵塞效应影响区时平均毛细上升速度也更快.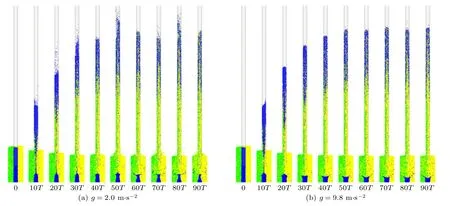
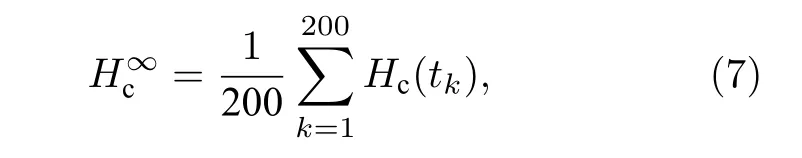
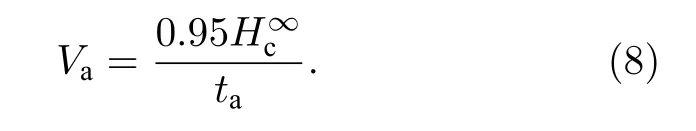
3.2 不同水平振动分量下颗粒毛细上升行为

3.3 不同粒径分布下颗粒毛细上升行为

4 结论
