爆炸冲击下试验台架数值模拟方法
2022-06-04莫昌锋周云波付条奇刘粟涛孙晓旺
莫昌锋,周云波,付条奇,张 明,刘粟涛,孙晓旺
(南京理工大学 机械工程学院, 南京 210094)
1 引言
现代战争中军用防护型车辆在执行任务的时经常面临着地雷和简易爆炸装置(improvised explosive device,IED)的威胁,其产生的爆炸冲击波不仅使车辆结构发生破坏,同时还会对车内乘员造成严重的生理损伤[1]。随着计算机数值仿真技术的成熟,有限元分析已经成为研究军用防护型车辆爆炸冲击响应的重要工具。由于地雷和IED发生爆炸时会在短时间内产生巨大的能量,因此在车辆防护领域中,研究准确高效的爆炸冲击数值模拟算法是这些年来的热点和难点问题。
LS-DYNA使用显示时间积分的高度非线性瞬态动态进行有限元分析,可以很好地模拟爆炸冲击过程。国内外学者在应用LS-DYNA进行爆炸冲击数值仿真上做了大量的研究工作,如毕程程等[2]研究了初始体积分数法在爆炸模拟中的应用,并将该方法结合ALE流固耦合算法在爆炸算例中进行可行性验证,得出了初始体积分数法定义的炸药在爆炸模拟很好地保证计算精度。曾爱等[3]对防爆油箱进行爆炸冲击响应数值模拟研究,分析了爆炸环境下燃油箱和燃油的动态响应过程。Thanh等[4]在LS-DYNA中分别应用了经验爆炸算法、ALE算法和拉格朗日-欧拉耦合算法分析爆炸载荷下钢板的受力情况。Slavik[5]提出了一种新的爆炸仿真方法,在拉格朗日结构周围的空气进行ALE建模,而对于远场爆炸则只需在ALE空气域的外表面与经验爆炸方程结合即可,该数值仿真方法扩展了LS-DYNA分析爆炸冲击新场景的能力。Samiee等[6]利用LS-DYNA的显示有限元分析,研究了聚脲对爆炸载荷下双层聚脲钢板性能的影响。
近年来,在对爆炸冲击问题分析的数值模拟上,由于ALE算法结合了拉格朗日算法和欧拉算法的优点,能很好地体现流体的运动规律,同时又能解决网格畸变的问题,因此ALE算法用来模拟爆炸冲击过程已经较为成熟且精度较高[7]。在进行爆炸分析时,ALE算法需要建立大量的空气和土壤单元,这导致ALE的计算时间比较长,造成计算效率不高。为了提高ALE算法的计算效率,LS-DYNA在ALE算法的基础上开发了一种新的算法,利用结构化网格来加快计算时间,这种算法称为结构化ALE算法(S-ALE)。王明振等[8]应用S-ALE流固耦合算法对飞机水上迫降进行数值分析,结果表明相对于传统的ALE耦合算法,S-ALE流固耦合算法较好地避免了流体的渗漏。Kurtolu[9]分别应用ALE算法和S-ALE算法模拟了钢结构舱体在爆炸冲击下的响应,研究表明采用S-ALE求解器时占用内存更小,并且在求解相同的模型下需要的时间更短。
本文中主要研究内容是用传统ALE算法和S-ALE算法对爆炸冲击试验台架进行数值模拟,比较这2种算法下钢板的最大残余变形和内能。最后进行台架实爆试验,验证并比较这2种算法的精确度,通过仿真和试验结果对比分析,S-ALE算法与试验结果更接近,计算时间更短。
2 爆炸仿真算法研究和有限元模型
2.1 爆炸仿真算法
传统的ALE算法和S-ALE算法的区别在于描述流场作用区域时是采用非结构化网格还是结构化网格。采用ALE算法分析时,LS-DYNA的ALE求解器会先读取网格元素和节点信息,然后根据这些信息输入来建立流场作用区域的非结构化网格,这个过程将会消耗大量的读取时间。S-ALE算法则将流场作用区域通过三维坐标来定义,LS-DYNA的S-ALE求解器根据三维坐标定义的几何信息直接生成结构化三维网格。结构化网格的特点就是网格内的节点与相邻的点连接关系是固定不变的,并且隐含在生成的网格中[10],这避免了求解模型时读取网格元素和节点信息的过程,加快数值计算的速度,并且使得模型占用的内存较少。同时结构化网格描述单元和节点的连接情况时简单明了,简化了ALE耦合时的搜索算法。
ALE算法和S-ALE算法在处理爆炸冲击问题时,都需要考虑爆炸流场与目标结构之间的耦合作用。基于多物质单元耦合模拟爆炸冲击过程是一种国内外公认成熟的仿真算法,该算法能很好地预测实爆试验的结果[11]。在仿真过程中,爆炸冲击波通过土壤、空气等介质传播,最后作用到目标结构,这个过程中流固耦合的控制主要通过罚函数来实现[12]。罚函数算法是检测到接触面发生穿透的时候,通过节点施加边界力,这个边界力定义为:
fi=-kidi
(1)
其中:fi为边界力;di是接触面间的穿透距离;ki是接触刚度。如图1所示,在接触边界上,罚函数法被认为每一个耦合点创建一个虚拟弹簧,接触刚度的定义为:
(2)
其中:fsi是接触面耦合比例因子;Kv、Al、Vl分别是体积模量、流体网格的断面面积和流体单元的体积。
2.2 有限元模型的建立
为了验证某试样钢板的抗爆炸性能,设计了埋爆炸药冲击试验台架,见图2。试验台架由底部支架、钢板固定支架以及配重块组成,材料都为Q235,其材料参数见表1所示。试样钢板的总体尺寸为1 500 mm×1 500 mm×20 mm,四周用高强度螺栓固定在试验台架上。根据爆炸试验要求,采用TNT圆柱形炸药,高径比为1/3,当量为8 kg,炸点位于试样钢板的正中间下方,炸药填埋深度100 mm。
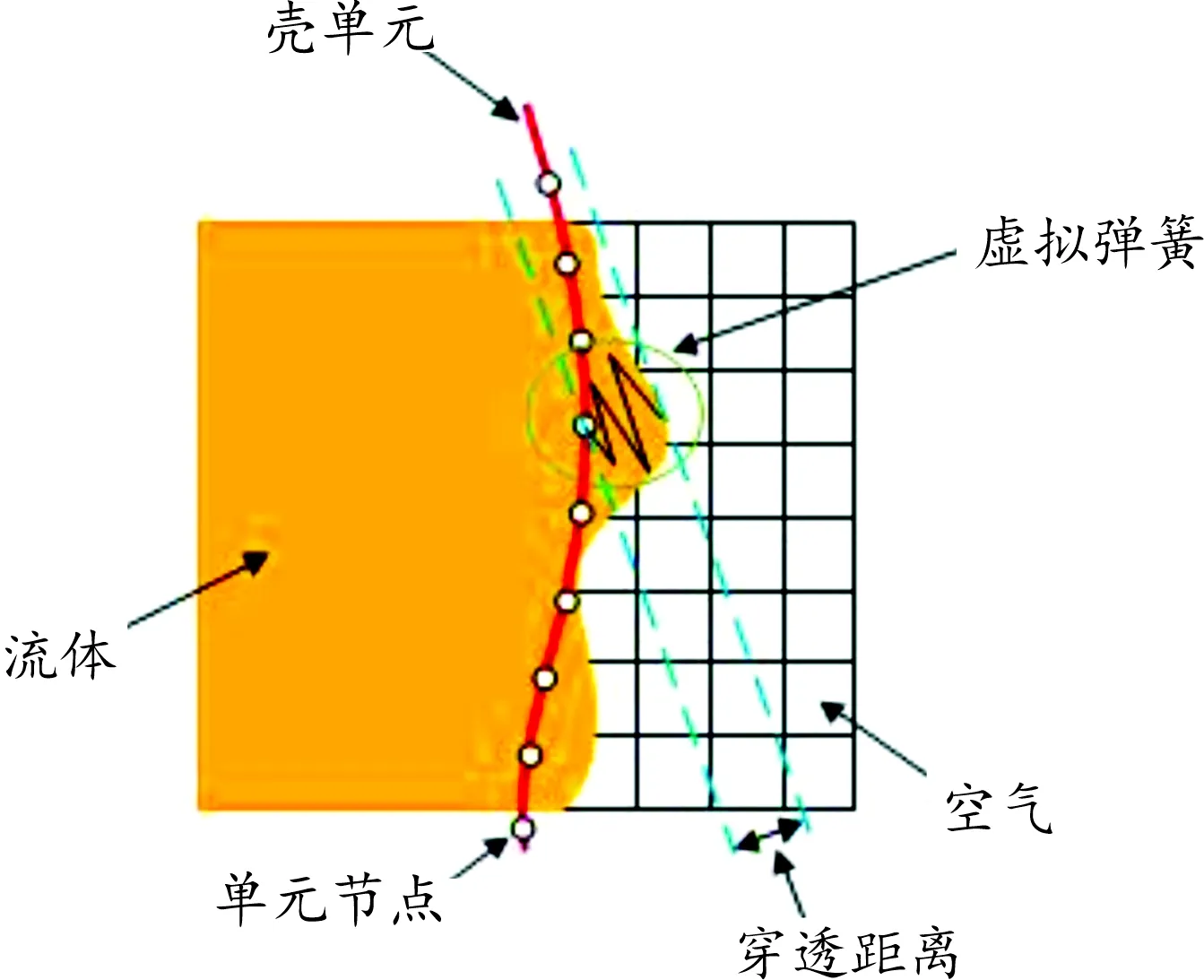
图1 流固耦合边界力示意图
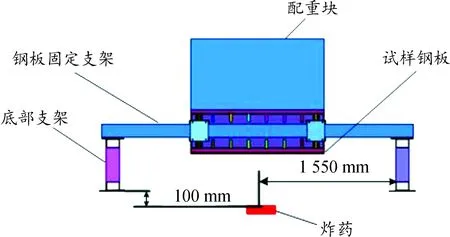
图2 试验台架示意图

表1 Q235的材料参数
在对台架以及试样钢板进行划分网格时,网格的基本尺寸为10 mm,除了配重块为实体单元,其余部分均为壳单元。采用ALE流固耦合的方法模拟爆炸冲击波作用于试样钢板,因此需要建立空气和土壤网格。空气网格区域只需要包含试验台架即可,空气和网格用实体单元建模,总尺寸为2 862 mm×2 600 mm×1 790 mm,土壤的高度390 mm,有限元模型见图3所示。
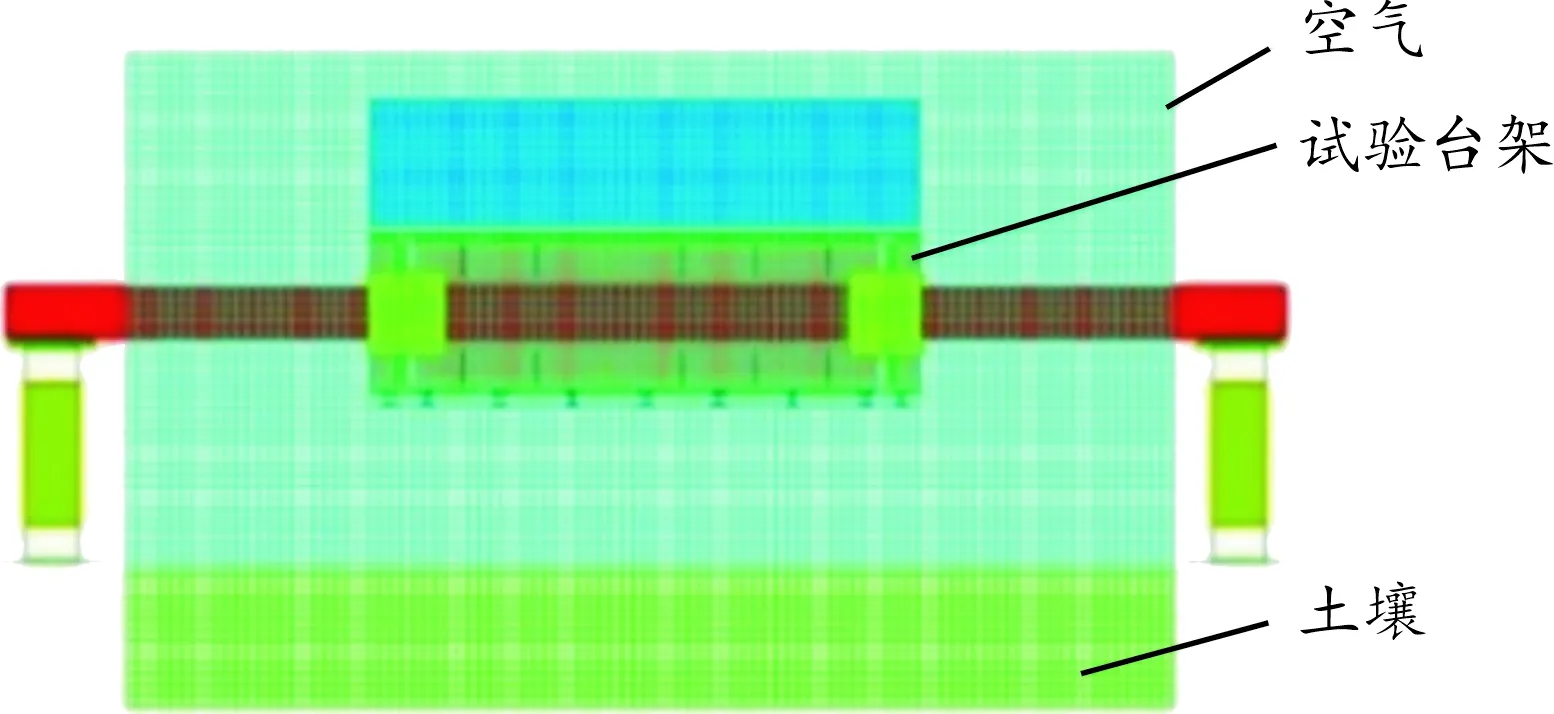
图3 试验台架有限元模型示意图
空气区域采用Mat-Null材料模型与线性多项式状态方程进行定义[13]:
P=C1+C2μ+C3μ2+(C4+C5μ+C6μ2)E
(3)
其中:P表示气体压力;Ci(i=1、2、3、4、5、6)为多项式方程系数;E为单位体积初始内能。这些参数对应的数值分别为:C0=-0.1;C1=C2=C3=C6=0;C4=C5=0.4;E0=0.253 mJ/mm3;V0=1[14]。土壤为超塑性材料模型,通过Mat_Soil_And_Foamble_Fail定义。
在LS-DYNA中,设置爆轰物气体的状态方程和材料参数来建立爆轰物的有限元模型。Jones、Wilkins和Lee(JWL)提出的半经验状态方程(EOS)描述了爆轰物气体的压力、能量和体积的关系,这个表达式为:
(4)
其中:A、B、R1、R2、ω是常数;E是单位体积能量;V是爆炸冲击过程气体产物相对于初始爆炸状态的相对体积。在LS-DYNA中通过EOS_JWL卡片来设置EOS参数,表2是TNT炸药的JWL的EOS参数[15]。
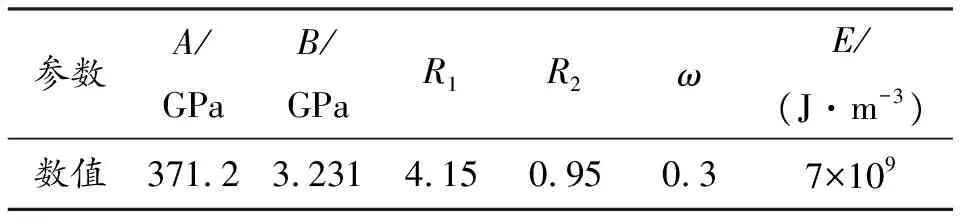
表2 JWL参数
通过MAT_HIGH_EXPLOSIVE_BURN设置TNT的物理参数,表3是TNT的物理参数[15]。
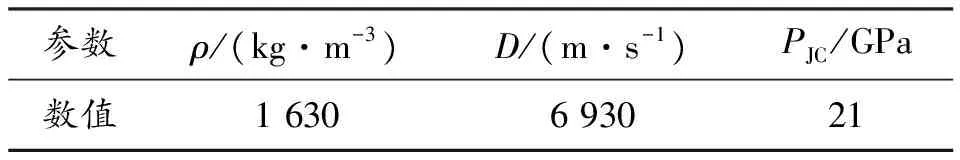
表3 TNT物理参数
由于使用对炸药用网格建模时,难以保证在有限元分析过程中的精度。初始体积法在处理流体模型是有着独特的优势,突破物质初始定义网格化的局限,并且在分析过程中能够保证计算精度[2]。因此在设置好炸药的状态方程和物理参数之后,通过初始体积法来定义炸药的形状,用 INITIAL_VOLUME_FRACTION_GEOMETRY关键字定义炸药的形状。
此外,在ALE流固耦合中,主要是用罚函数法来描述耦合关系,用CONSTRAINED_LAGRANGE_IN_SOLID这个关键字卡片来设置耦合关系。为了模拟无限空气和土壤域,在空气与土壤网格的外表面设置无反射边界条件。整个有限元模型单元数为664 207,节点数为685 323。
同时使用结构化ALE(S-ALE)算法进行分析,这是LS-DYNA开发的一种新算法。S-ALE算法利用结构化网格的特征来加快求解模型的速度,提升数值分析的效率。S-ALE流固耦合方法很多控制卡片的设置和ALE流固耦合方法是相类似的。在本研究中,针对空气域和土壤域不再使用实体单元建模,而是重新在LS-DYNA中建立空气和土壤的结构化网格,分别通过ALE_STRUCTURED_MESH和ALE_STRUCTURED_MESH_CONTROL_POINTS这两个新的关键字卡片来控制,并且通过这个设置在求解模型时调用S-ALE求解器,除了这2个卡片设置外,其他大部分设置与上述的ALE流固耦合方法是一样的。
3 数值仿真结果与讨论
3.1 ALE算法仿真结果
爆炸冲击下台架的试样钢板的变化如图4所示。在爆炸冲击波的作用下,0.7 ms钢板发生变形向上凸起,并且在4.2 ms时刻钢板向上凸起的变形最大。图5是钢板的最大变形的位移云图和最大变形点位移曲线,可以看出,在4.2 ms之后,钢板的向上凸起的变形量略有下降,这是由于钢板存在弹性变形和塑性变形,弹性变形部分后面逐渐恢复。在8 ms到12.5 ms之间,钢板的最大变形量逐渐趋于稳定,因此仿真计算时间到12.5 ms。
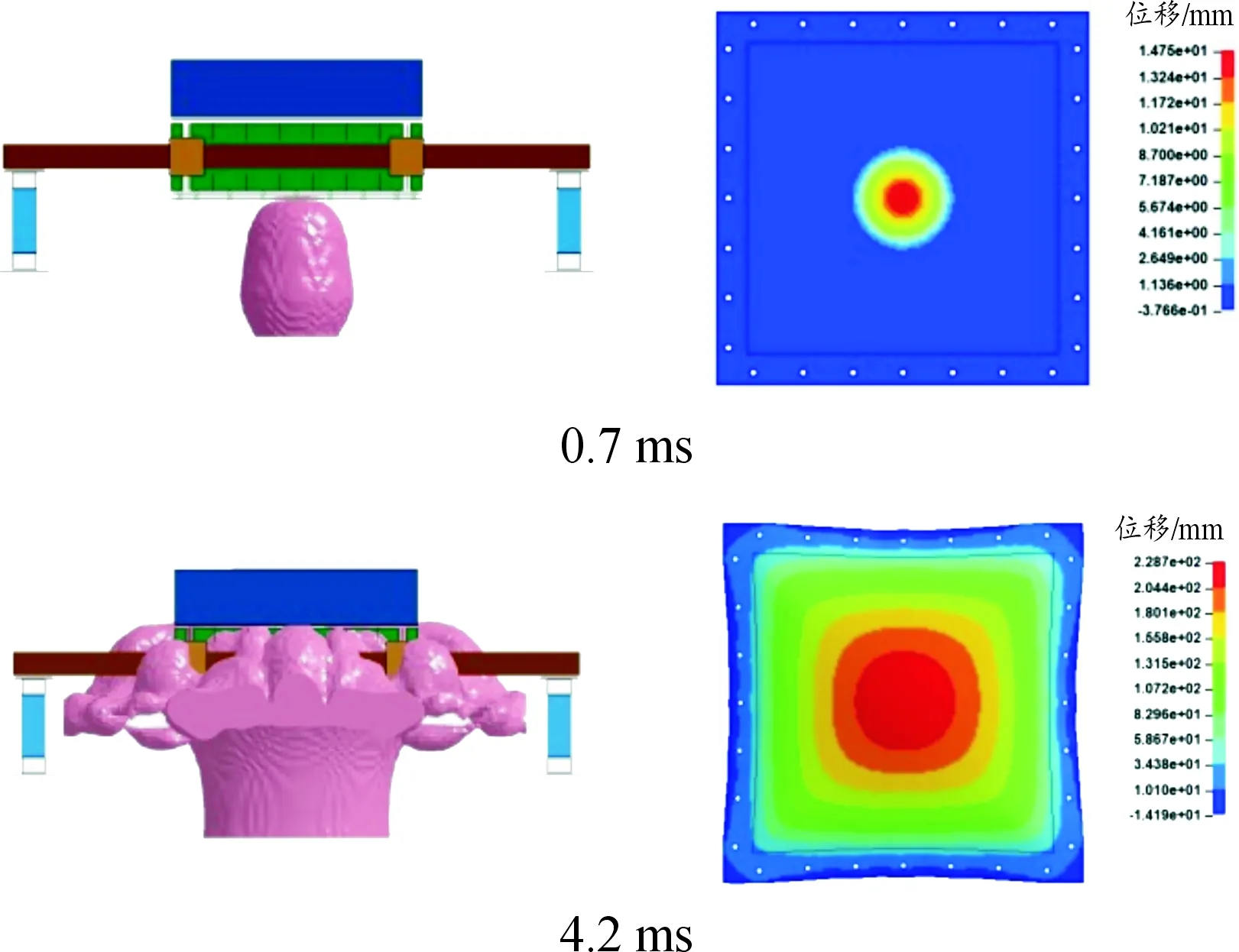
图4 ALE算法仿真结果云图
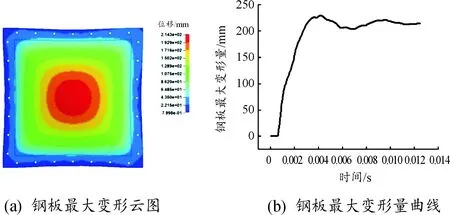
图5 ALE算法钢板仿真结果云图
3.2 S-ALE算法仿真结果
S-ALE算法仿真结果见图6所示。从仿真动画来看,试样钢板变形的大致趋势和ALE算法相类似。在0.7 ms爆炸冲击波使得钢板开始发生变形,在4.2 ms钢板变形量达到最大。钢板变形云图与最大变形点位移曲线见图7所示,8~12.5 ms钢板变形量趋于稳定。
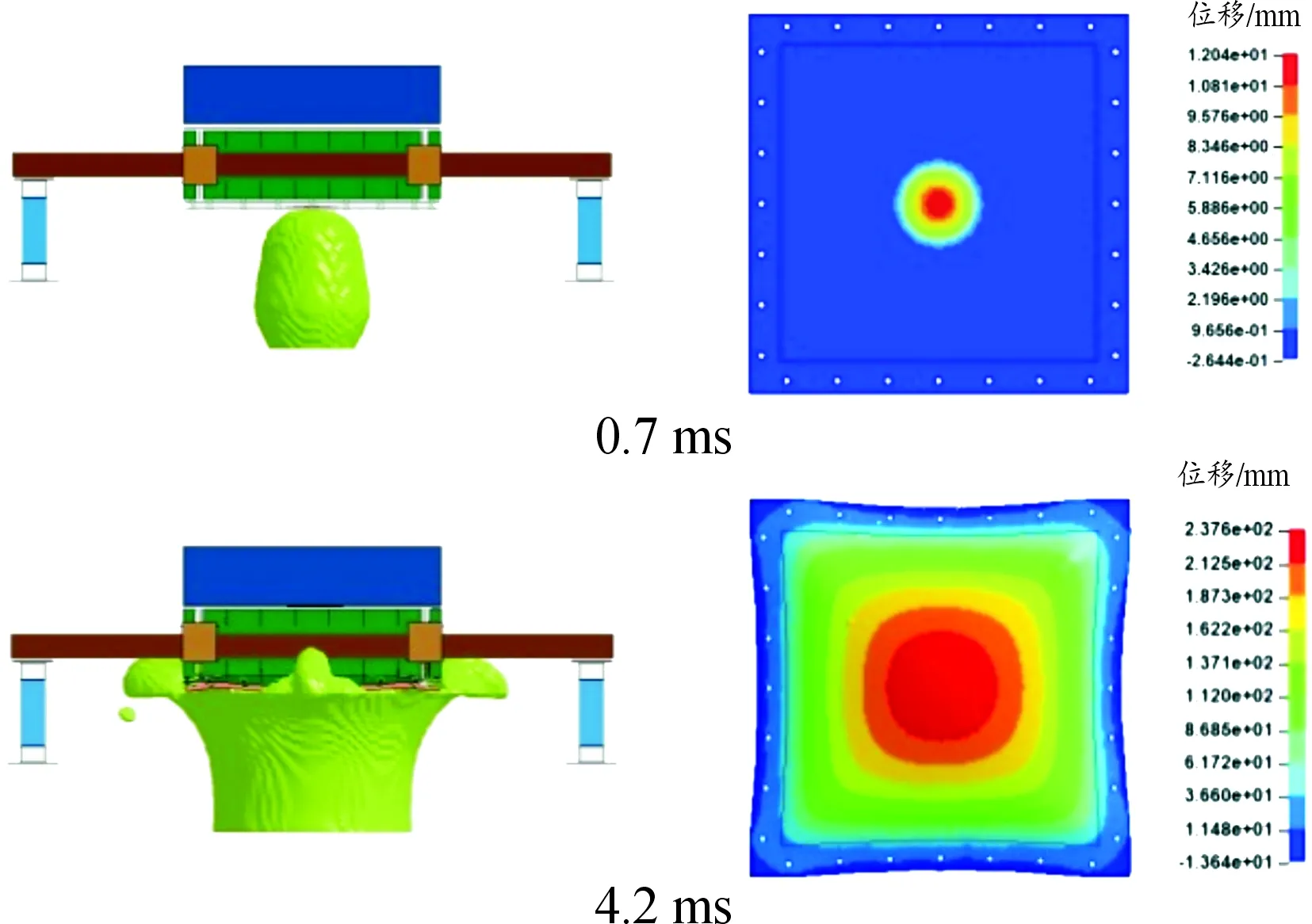
图6 S-ALE算法仿真结果云图
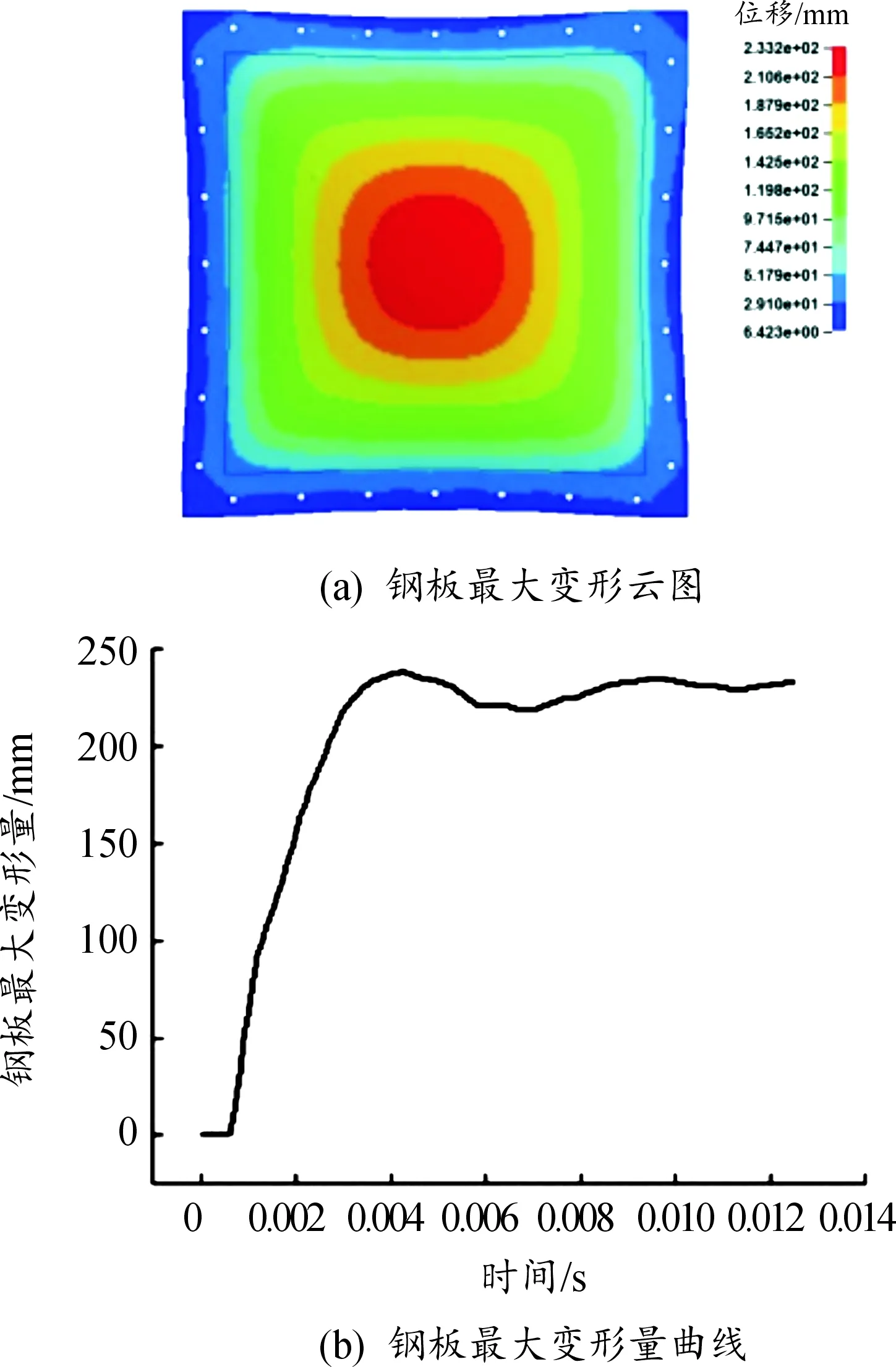
图7 S-ALE算法试验钢板仿真结果
3.3 2种数值模拟方法对比
1) 通过钢板最大变形量曲线可以看出,ALE算法计算得到的试样钢板最终的最大变形量为214.260 mm,S-ALE算法计算得到的试样钢板最终的最大变形量为233.171 mm。
2) 图8显示2种算法在爆炸冲击波作用到钢板时的流固耦合控制,可以看出,ALE算法在仿真过程中出现了爆炸冲击波流体渗漏,而S-ALE算法则在仿真过程中流体得到有效的控制。
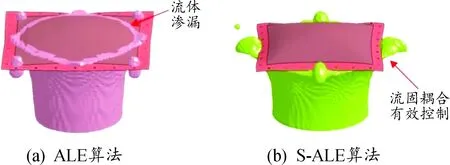
图8 2种算法流固耦合控制云图
3) 图9是2种算法试样钢板的内能曲线,从曲线可以看出,2种算法总体趋势类似,但S-ALE算法的试样钢板内能更大,这是因为仿真中S-ALE算法能进行有效的流固耦合控制,使得爆炸冲击波作用在钢板上的力更大,钢板产生更大的变形。
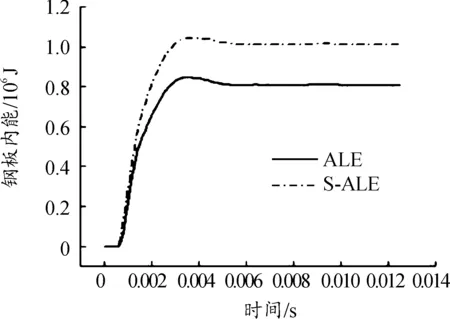
图9 钢板内能曲线
4) 2种算法在计算时间上,S-ALE算法需要的时间更短,计算效率更高。
4 台架试验
4.1 试验内容与布置
本次冲击台架试验目的是测试某型号钢板抗爆炸冲击性能,并通过试验结果验证前期数值分析的精度。
由于爆炸试验历时短,可重复性差且危险性高,因此在试验之前必须做好充足的试验准备。根据试验标准的要求,制作的试验台架如图10所示。试验前还需测量台架正面与侧面的水平度,如图11所示。试验台架除了试样钢板外均由Q235材料制造而成。钢板与台架用M20的高强度螺栓进行连接固定,两根支撑横梁由安装台架外部贯穿放置于支撑座上,靶板下表面距地面400 mm。试验台架顶部增加配重,配重均匀,台架重约1.5 t,顶部配重块约7.5 t。炸药由TNT制成,当量为8 kg,圆柱状,埋藏深度为100 mm。炸药放置在标定的起爆位置之后,起爆体与设置在200 m以外的起爆装置连接,最后炸药在距离钢板500 mm中心处被引爆。

图10 爆炸冲击试验台架实物图

图11 正面与侧面水平度测量现场图
爆炸后台架的整体状况如图12和图13所示。台架一侧陷入沙坑,横梁出现折弯,配重块未脱离;试样钢板与台架的连接螺栓全部断裂脱离,螺栓孔变形;钢板背凸形成鼓包,未出现裂纹。

图12 试验后台架实物图

图13 试验后钢板实物图
试验后钢板发生变形,无裂纹产生,为了测出钢板的变形量,因此采用3D扫描仪成像系统测量钢板爆炸后的变形量,测量面为背爆面,扫描成像见图14所示。经过测量,钢板的变形量为231.047 mm。

图14 钢板3D扫描成像图
4.2 仿真与试验对比分析
根据试验和仿真的分析,对比2种算法与试验的钢板变形情况见图15所示,可以看出,S-ALE算法计算的结果与试验值更接近。2种算法计算结果与试验实测结果见表4所示。
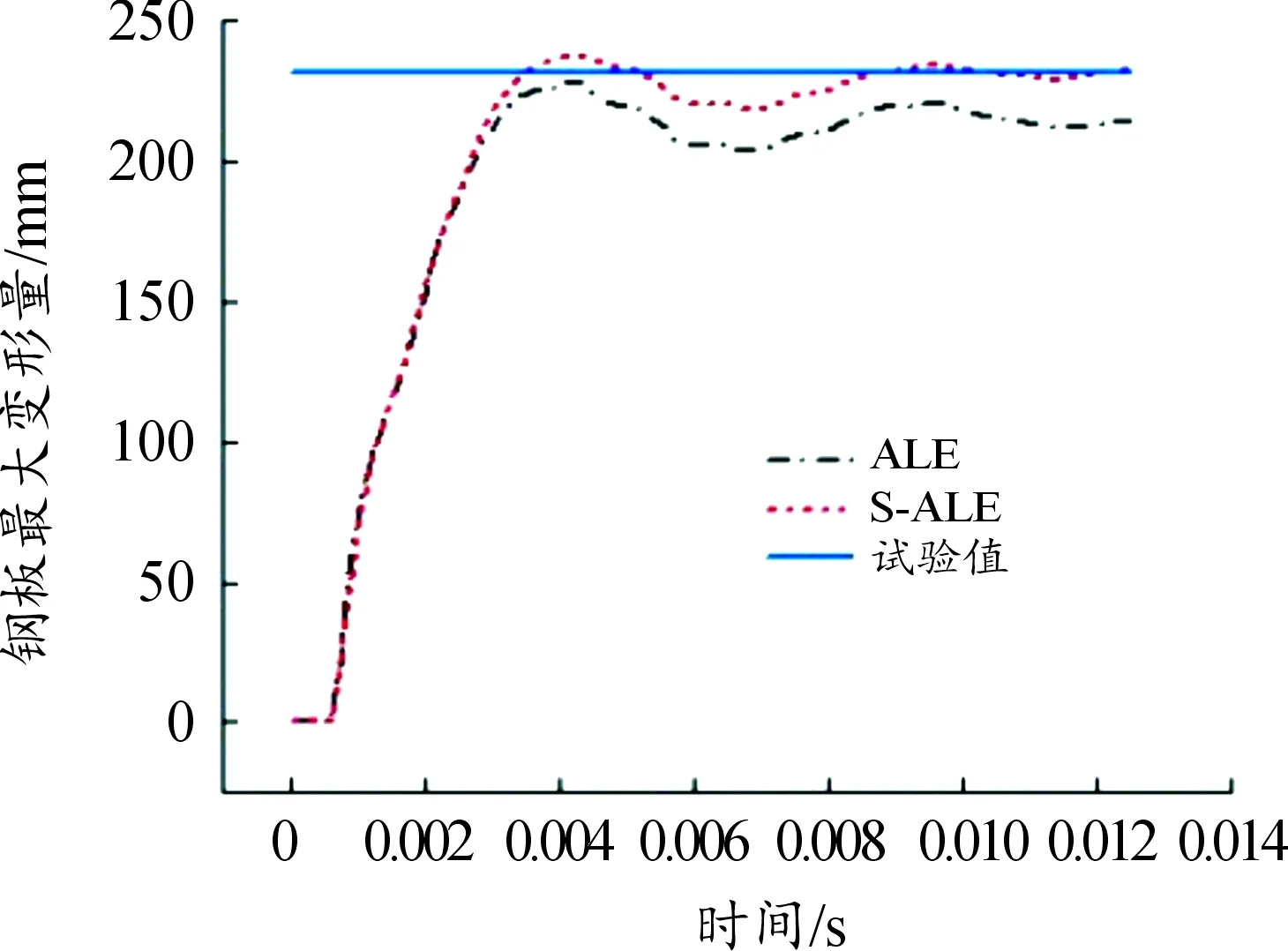
图15 钢板变形量曲线

表4 仿真结果与试验结果
ALE算法计算的钢板变形量与试验值的误差为7.27%,而S-ALE算法计算结果的误差为0.92%;S-ALE算法计算的时间比ALE算法的少4 593 s;对比分析可知,S-ALE算法的计算精度更高,计算时间更短。
5 结论
1) 采用了ALE算法和S-ALE算法模拟炸药埋爆冲击台架试验,对比了2种算法在仿真过程中的差异。采用ALE算法模拟时,在仿真过程中出现了爆炸冲击波流体渗漏,而S-ALE算法则很好地避免了流体的渗漏,在模拟爆炸冲击波作用到钢板过程中,进行了有效的流固耦合控制,使S-ALE算法计算结果与试验结果更加接近,计算精度更高。
2) 对比分析2种算法在钢板变形量和内能的差异,发现在前2 ms内的计算结果吻合度较好,而后面由于ALE算法的流体产生渗漏,导致计算结果产生差异。
3) 与ALE算法相比,S-ALE算法仿真结果与试验实测结果更吻合,计算精度更高,计算时间更短。因此,S-ALE算法在模拟爆炸冲击时展现出较大的应用潜力。
