基于波形相干成像条件的微地震偏移定位方法

王金龙， 张建中， 黄忠来， 陈 杰， 秦 亮

(中国海洋大学 1. 海洋地球科学学院; 2. 海底科学与探测技术教育部重点实验室， 山东 青岛 266100)

水力压裂是开采非常规油气资源的一种有效技术手段，它主要通过钻井向地下储层注入压裂液，来改变地下储层的渗流状态，形成人工裂缝网络，提高储层中流体的流动性，增加油气产量[1-2]。微地震监测技术作为评价水力压裂效果的重要方法近年来得到了快速发展，它的主要作用是评估压裂施工的效果，估算储层的改造量以及改进压裂工艺等，并且通过实时监测可以现场指导水力压裂施工，还可以对以后的二次开发起到指导作用[3-5]。

微地震监测方式可分为井中监测、地面监测和井-地联合监测等[6]。其中井中监测的检波器受到地面上的噪声影响较小，微震记录的信噪比较高，但井中监测必须要有合适的监测井，需要将检波器放在深井中，操作难度大、施工成本高，同时成像孔径不够会导致震源定位结果不准。地面监测的检波器放置在地表，具有施工方便、成本低、成像孔径大等优势。然而，地面检波器距离压裂目标区较远，接收的微震信号很弱，噪音可能会淹没微震信号，很难识别微地震事件，使基于走时反演的定位方法受到了限制。基于偏移叠加的定位方法不需要拾取微震信号的初至到时，直接利用波形信息进行震源定位，并且在震源定位过程中可以压制噪音，特别适用于地面微地震监测，成为近年来的研究热点[7-9]。

Kao和Shan在2004年首次提出了震源扫描法，并利用亮度函数来计算地下所有网格点的成像能量值，通过搜索成像能量的最大值确定震源的空间位置和发震时刻[10]，亮度函数在计算中对微震记录振幅取绝对值后叠加，增强了噪音的影响，对低信噪比的微震资料处理效果不好。Tchebotareva等利用多道微震记录的波形相似性来构造成像函数，通过直接叠加微震记录的波形进行震源定位，能够有效地压制噪音对震源定位结果的影响[11-13]，但该方法受微震信号初至极性影响较大，导致震源定位结果不准。Trojanowski和Eisner通过对基于偏移叠加的微地震定位方法进行对比分析，表明利用震源机制对微震记录进行极性校正后再叠加能够显著提高震源的定位精度[14]。为了克服极性反转的影响，Anikiev等提出了一种可以同时反演震源机制和震源位置的方法[15]，但需要很大的计算量。何勇等在震源扫描法的基础上，同时扫描震源机制，在亮度函数中引入了初动极性改正项，提高了震源定位精度，但扫描震源机制降低了计算效率[16]，难以用于微震实时监测。

为了解决微震资料的低信噪比和极性反转导致震源定位不准的问题，本文利用微地震记录中来自地下同一个微震信号波形所具有的相干性来构造成像函数。与常用的相似性成像函数直接叠加微震记录的振幅不同，该成像函数先计算相邻检波点微震记录的相干系数，然后对相干系数叠加得到成像能量值。理论模型测试和实际资料应用证明本文方法可以有效地压制噪音，并解决了极性反转的问题，提高了震源的定位精度。

1 方法原理

基于偏移叠加的定位方法主要是利用微震记录的波形进行震源定位，首先将目标监测区域划分成网格单元，计算所有网格点到每个检波点的走时；然后利用走时差对微震记录进行时差校正，再应用成像函数得到能量值，直至遍历所有网格点；最后通过确定成像函数的极大值，得到震源参数。

1.1 基于偏移叠加的震源定位原理和步骤

(1)首先根据监测区域确定目标范围大小，对该区域按照一定网格大小进行模型离散化，如图 1(a)所示，其中的所有网格点被看作是可能的震源点。

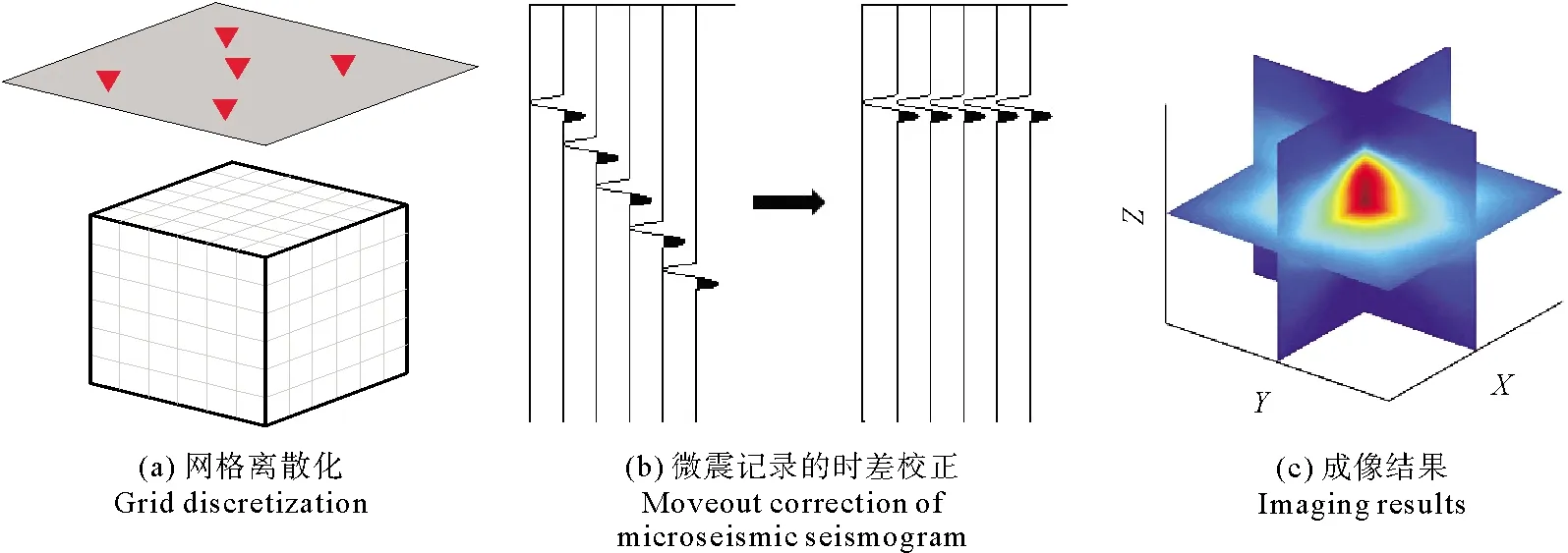
图1 基于偏移叠加的微地震定位方法流程示意图Fig.1 The flow diagram of microseismic location method based on migration stacking

(2)建立一个准确的速度模型，利用射线追踪方法计算所有网格点到达地面检波点的走时。选择一个检波点ref作为参考检波点，参考检波点的选取决定了同相轴拉平的位置，对震源定位结果没有影响。对于所有网格点计算各检波点相对参考检波点的走时差，任意网格点η的走时差Δtη可以表示为：

Δtη=([t1-tref,…,tn-tref,…,tN-tref])η,
n=1,2,…,N。

(1)

其中：tn表示网格点η到检波点n的走时；tref表示网格点η到参考检波点ref的走时；N表示所有检波点的总数。

(3)在发震时刻τ下，对于任意网格点η，根据走时差Δtn对所有检波点的微震记录做时差校正，如图1(b)所示，之后应用成像函数叠加得到网格点的成像能量值E(η,τ)。

(4)按照步骤(3)计算目标区域内所有网格点的成像能量值，如图 1(c)所示，最后通过成像函数的能量极大值确定震源位置。

1.2 成像函数

成像函数是基于偏移叠加的震源定位方法的关键。常用的相似性成像函数[12]可以表示为：

(2)

其中：S(η,t)表示对于地下任意网格点η在发震时刻τ的成像能量值；tηn表示网格点η到检波点n的走时；k表示选取时间窗口的第k个采样点，一共2W+1个采样点数；un表示第n个检波点的微震记录振幅值；N表示检波点总数。

上述常用成像函数对偏移后的微震记录的振幅直接叠加，可以压制噪音的干扰。但当微地震信号初至存在极性反转，这种成像函数会削弱有效信号的叠加能量，导致震源定位结果不准或者遗漏微地震事件。为了解决该问题，本文利用各个检波器记录的同一个微震信号波形具有的相干性，来构造成像函数。对时差校正后的微震记录，先计算相邻检波点微震记录的相干系数，然后对相干系数进行叠加得到成像能量值。该成像函数可表示为：

(3)

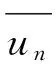
(4)

其中，k表示选取时间窗口的第k个采样点，一共2W+1个采样点数。相干系数表示时间窗口内相邻两个检波点波形的相似程度。如果两个相邻检波点的波形不相干，如随机噪音，则计算的相干系数接近0；如果两个相邻检波点的波形相似程度高，若极性相同则相干系数接近1，若极性不同则相干系数接近-1。微震信号的初至极性往往呈区域性分布，所以绝大多数相邻检波点的极性是相同的，相干系数接近1，只有在正、负极性区域交界处，相邻检波点的极性是不同的，相干系数接近-1。这样，极性不同的相邻检波点波形比极性相同的相邻检波点波形的数量要少得多，所以将所有相邻检波点的相干系数叠加后，极性不同的相干系数对成像函数影响很小，从而解决了初至极性反转对微震定位的影响。

2 理论模型数据测试

本文模拟三维速度模型的微地震记录，对成像函数进行测试。速度模型大小为3 000 m×3 000 m×2 500 m，离散网格大小为5 m×5 m×5 m，由四层介质组成，从上到下各层速度依次是3 000、3 500、40 00和45 00 m/s，如图 2(a)所示。为了符合野外实际观测情况，地面监测系统采用星型布设方式，一共8条测线，每条测线上共7个检波器，检波器间距为200 m，共有56个检波器，如图 2(b)所示。使用时间二阶，空间十二阶的三维声波方程有限差分算法进行波场正演计算合成微地震记录，震源采用主频为60 Hz的雷克子波信号，时间采样间隔为0.5 ms。

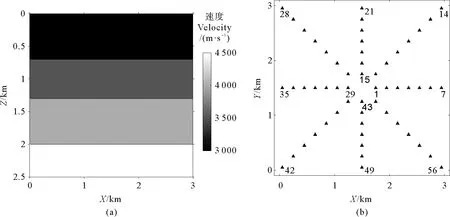
图2 (a)速度模型；(b)地面监测系统Fig.2 (a) Velocity model; (b) Surface monitoring geometry

本文微震记录中加入一定强度的高斯白噪声来模拟地面微地震资料低信噪比的情况，定义平均信噪比(Signal-to-noise ratio, SNR)[17]为：

(5)

其中：RMSsignal是微震信号振幅的均方根；RMSnoise是随机噪音振幅的均方根；N是检波点总数。

为了测试成像函数对存在极性反转情况的微地震记录的适用性，设计了双力偶震源，震源机制参数为方位角120°、倾角90°、滑动角180°，震源位置为(1 500,1 500和2 000 m)。图 3(a)为合成的存在初至极性反转的无噪音微地震记录，其中第1道至第14道和第29至第42道为正极性，第15道至第28道和第43道至第56道为负极性，图 3(b)为加入一定强度噪音后信噪比为0.5的合成微震记录，可以看出有效微震信号已经完全淹没在噪音中，无法识别。

图3 合成的初至极性反转微地震记录Fig.3 Synthetic first break polarity reversal microseismic seismogram

首先对理论模型的目标监测区域进行网格离散化，区域范围在X、Y、Z三个方向分别是1 000～2 000 m、1 000～2 000 m、1 500～2 500 m，离散网格大小均为5 m。然后利用基于斯奈尔定律的射线追踪方法[18]计算地下每个网格点到地面检波点的走时。图 4(a)和(b)是利用常用的相似性成像函数和本文方法对存在初至极性反转的微地震资料的定位成像结果。常用成像函数在真实震源位置附近出现了多个能量团，在真实震源位置没有能量聚焦，说明初至极性对该成像函数影响较大，其主要原因在于常用成像函数对时差校正后的微震记录直接叠加，由于存在极性反转的情况，微震记录的振幅相加正负抵消，使得叠加后成像能量值偏小，定位结果不准确。而本文方法不受极性反转的影响，定位成像区域聚焦效果明显，定位结果与实际震源位置重合，实现了震源的准确定位。

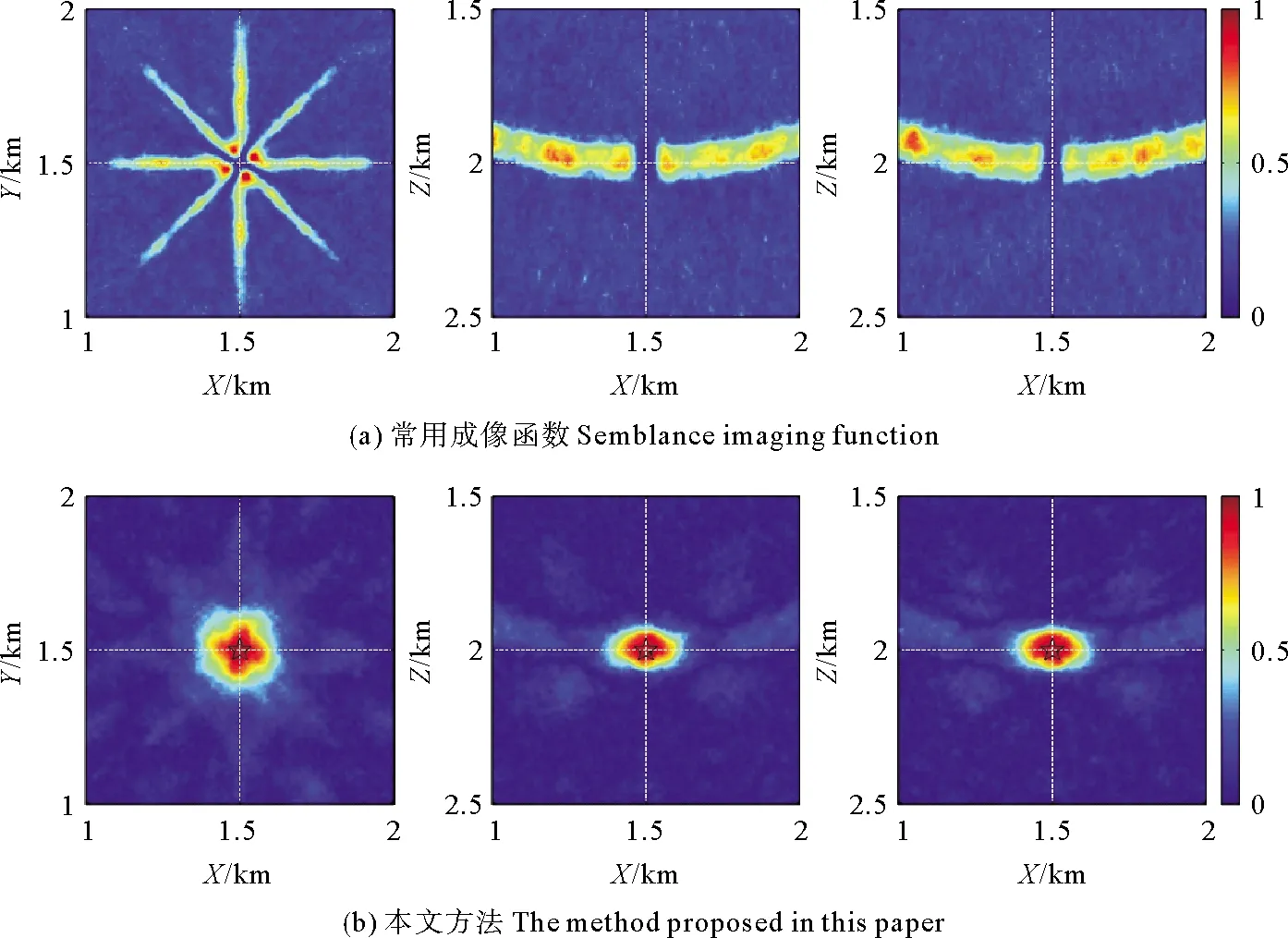
(第一列表示XY切片，第二列表示XZ切片，第三列表示YZ切片。两条白色虚线交点表示实际震源位置，黑色五角星表示定位结果，即成像能量最大值点。The XY slices are represented in the first column, the XZ slices are represented in the second column, and the YZ slices are represented in the third column. The real source location is indicated by the intersection of the two white dashed lines. The black stars indicate the calculated locations (i.e., the maximum values of the image functions).)图4 初至极性反转的微震记录的定位成像结果切片图Fig.4 Location imaging results of microseismic seismogram with first break polarity reversal

3 实际资料应用

为了验证本文方法的有效性，使用实际地面微地震资料进行测试。如图 5(a)所示为该工区的地面监测系统，以井口为中心，呈放射状布设8条测线，共计449道，检波器间距40 m，采用星型布设方式，井口坐标为(0 m，0 m，0 m)，距离井口最小偏移距58 m，最大偏移距为3 480 m，地面检波器覆盖范围广，成像孔径满足了微地震监测的要求。根据声波测井速度曲线建立地层速度模型如图5(b)所示。对实际微地震资料进行带通滤波和静校正等预处理，图 6显示了第1条测线和第2条测线的微地震记录，可以看出地面微地震资料信噪比较低，同时该微震信号存在明显的初至极性变化，其中第1道至第12道和93道至105道为正极性，第13道至第92道为负极性。

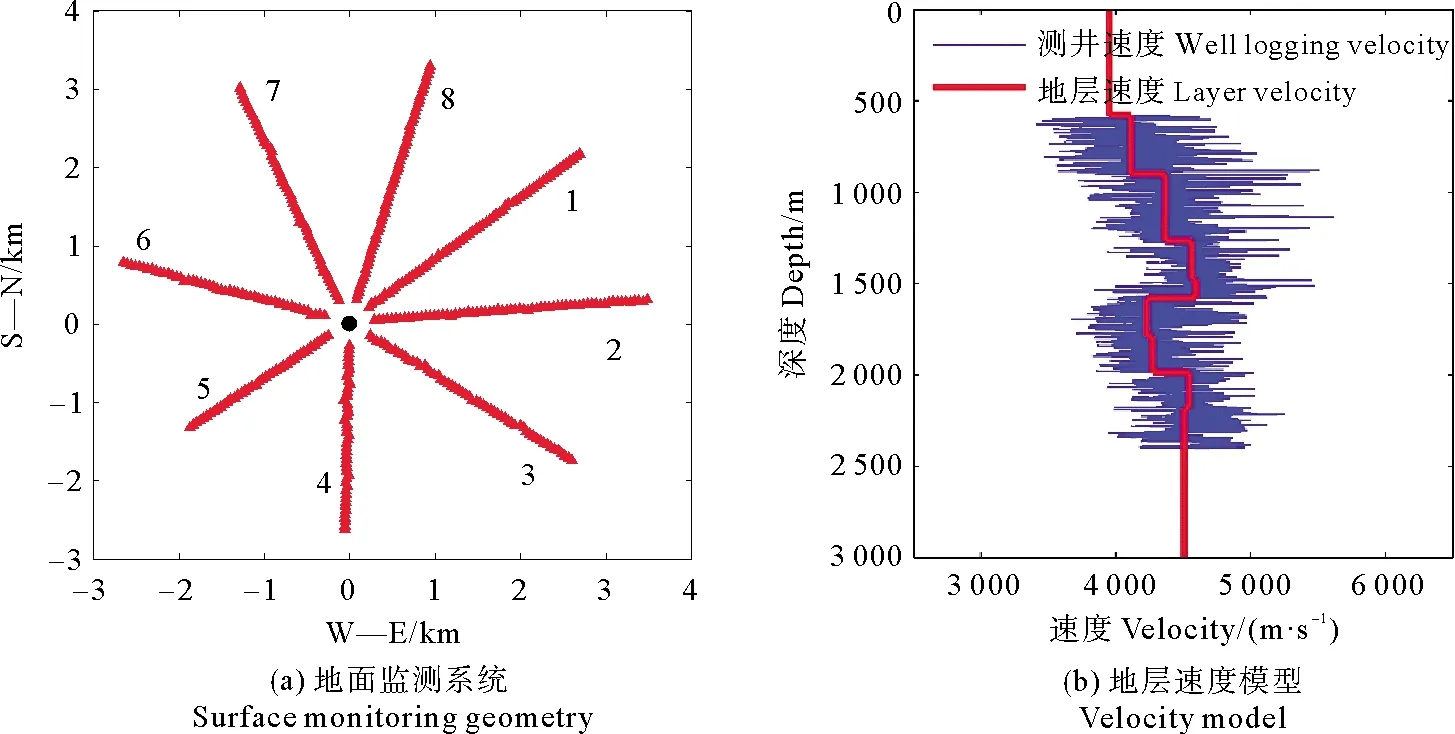
(红色三角表示地面检波点，黑色圆点表示井口位置，数字表示测线编号。The red triangle denotes receivers, the black dot denotes the position of the wellhead and the number denotes the line number.)图5 (a)地面监测系统；(b)地层速度模型Fig.5 (a) Surface monitoring geometry; (b) Velocity model

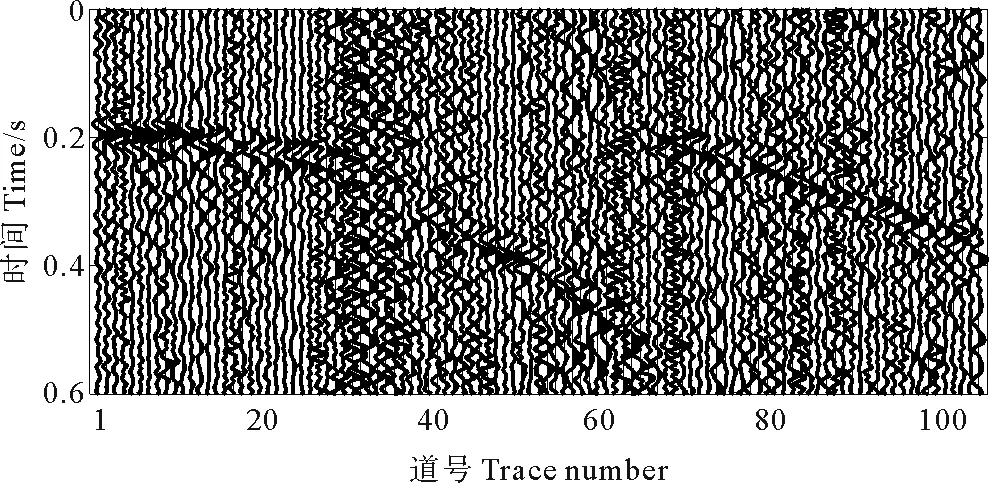
图6 低信噪比的实际地面微地震资料Fig.6 Surface microseismic data with low signal-to-noise ratio

根据压裂段的实际射孔位置确定成像区域范围，在X、Y、Z三个方向范围分别是0～1 000、0～1 000和2 000～3 000 m，离散网格大小均为5 m。然后用射线追踪方法计算每个网格点到地面检波点的走时。图7(a)和(b)是常用相似性成像函数和本文方法处理实际微地震资料的定位成像结果。可以看出常用成像函数的定位成像结果因微震信号存在极性反转的情况，出现震源辐射花样特征，并且存在多个能量团，定位结果不确定；使用本文方法在定位过程中消除了极性反转的影响，震源的定位结果为(500, 470和2 440 m)与压裂井中实际的射孔位置相近，震源定位结果可靠，说明了本文方法的有效性。

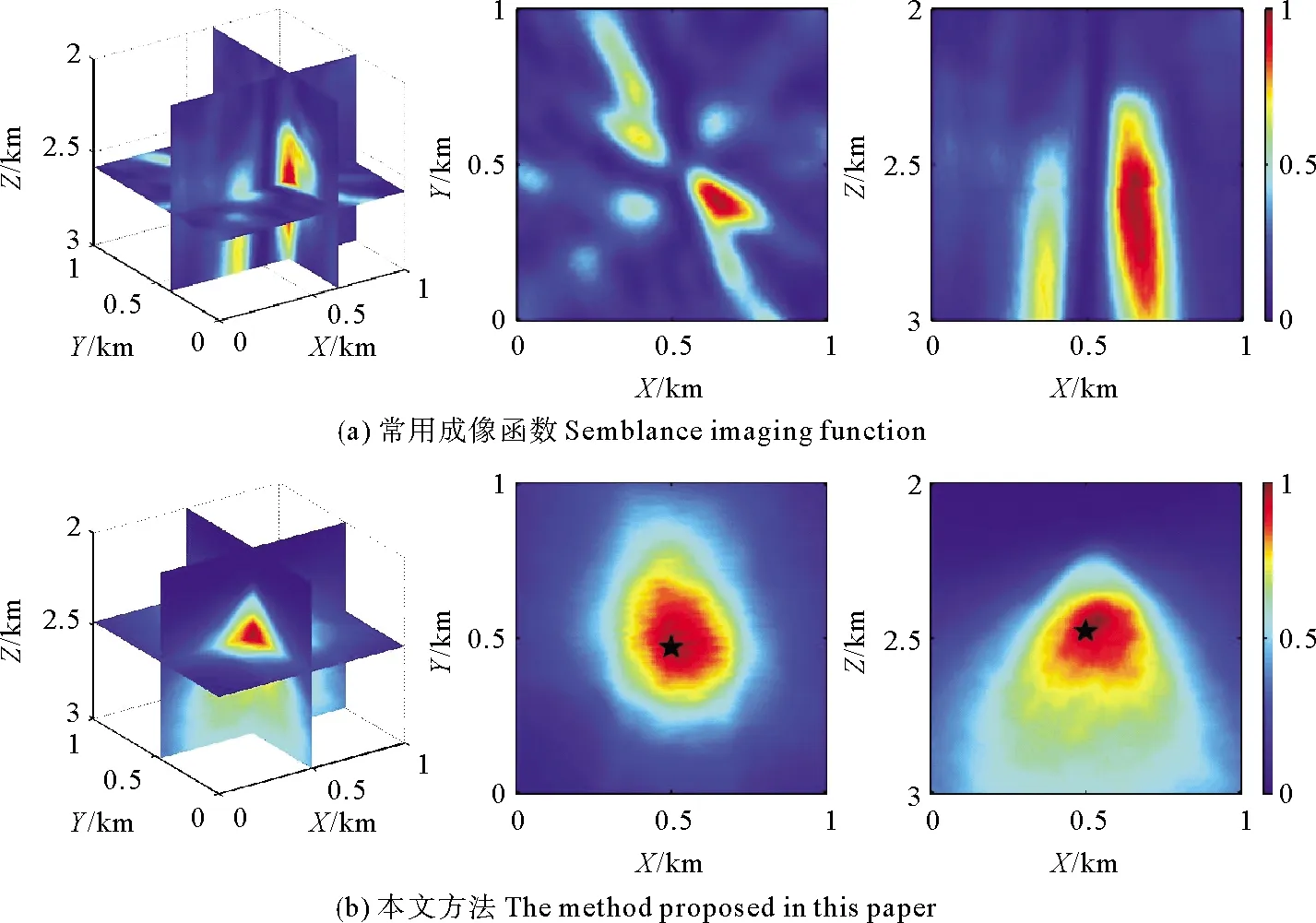
(第一列表示三维切片，第二列表示XY切片，第三列表示XZ切片。黑色五角星表示定位结果，即成像能量最大值点。The three dimensional slices are represented in the first column, the XY slices are represented in the second column, and the XZ slices are represented in the third column. The black stars indicate the calculated locations (i.e., the maximum values of the image functions).)图7 实际地面微地震资料的定位成像结果Fig.7 Location imaging results of surface microseismic data

4 结语

地面微地震资料存在初至极性反转，常用的相似性成像函数直接叠加微震记录的振幅值，会导致微震信号相互抵消，降低了震源定位精度；低信噪比微地震资料的震源机制反演比较困难，容易产生多解性，计算量较大，因此利用震源机制校正初至极性的震源定位方法也具有一定的局限性。本文提出了一种基于波形相干成像条件的微地震偏移定位方法，利用相邻检波点微震记录的相干系数叠加计算成像能量值，以此消除初至极性反转的影响。模型测试和实际微震资料应用表明，本文方法能够有效地压制噪音，解决了初至极性反转的问题，可以更好地处理低信噪比的地面微地震监测资料。