基于变模量本构模型的三维地基沉降计算分析

2022-06-03王东英杨光华周小文李卓勋

煤炭学报 2022年5期

王东英，杨光华，周小文，姜燕，李卓勋

(1. 广东省水利水电科学研究院岩土工程研究所，广东广州 510610；2. 广东省岩土工程技术研究中心，广东广州 510640；3. 华南理工大学土木与交通学院，广东广州 510640)

随着空间资源集约复合利用需求的提出，深大、复杂地质条件基坑的建设需求不断增加，对精准计算地基沉降提出了更高的要求，当前地基沉降计算不准一直是令工程师头疼且亟待解决的问题。

目前地基沉降分析方法主要有以分层总和法为代表的传统解析方法和考虑复杂本构模型的数值方法。分层总和法以“各向同性均质线性变形体”为假设前提，此假设与土的实际情况有较大出入，不能反映弹塑性或塑性状态下土的变形特征，同时因计算参数采用室内压缩试验获取，不仅取样扰动干扰参数取值，而且不能反映现场应力状态，经验系数的选取也存在很大的人为性。针对这一问题，杨光华等基于现场载荷板试验曲线，提出了分层总和法的修正方法—原位土的双曲线切线模量法和割线模量法，以切线模量替换压缩模量及其经验系数，极大的减少了扰动误差，并考虑了应力状态对变形参数的影响，对于均质或规则地层沉降分析具有较高的准确度。但对于地层分布复杂的三维地基沉降分析，该方法也具有其局限性，因此，尚需探索与该方法相适应的数值方法求解三维地基沉降问题。Mohr-Coulomb本构和小应变硬化本构是当前沉降计算应用较多的本构模型，但本构模型的适用性和参数的选取存在较多问题。Mohr-Coulomb本构不能反映土体的非线性及小应变刚度特征；小应变硬化模型考虑了土体的小应变刚度特征和非线性特性，但涉及参数较多，且想要准确取值较为困难。因而有必要探索既能反映土体刚度特征和非线性特性，同时参数取值可靠的本构方法。

基于上述问题，笔者基于C++将与切线模量法相适应的变模量本构嵌入到FLAC3D中，该本构模型可以使土体模量随应力水平变化从而实现土体的非线性特征，对应参数较少，且取值方法成熟。依托荔湾大厦基坑工程，对大面积、大荷载和复杂地质条件下的三维地基沉降和应力分布特征进行分析，并将沉降结果与工程实测值进行对比，充分证明变模量本构在求解复杂地质条件下三维地基沉降分析中的优越性和适用性。同时分析了基础形状、基础刚度、荷载大小及地层条件对地基沉降及应力分布特征的影响，证实对于基础刚度较大、荷载较大或不对称不等厚地层，应慎重选择数值分析方法，以免造成对地基承载可行性和结构可靠性的误判。

1 变模量本构及参数确定

1.1 变模量本构

变模量本构是杨光华等基于Duncan-Chang模型及原位土的-曲线提出的，其中心思想为土体的变形模量随应力水平的增大而呈非线性降低，土体屈服前，存在非线性弹性变形阶段。应力水平的表达式为

(1)

式中，为应力水平；为最大主应力；为最小主应力；(-)为极限强度。

基于Mohr-coulomb屈服准则的极限强度为

(2)

式中，为黏聚力；为内摩擦角。

切线模量随应力水平的变化关系为

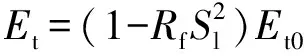
(3)

式中，为破坏比，一般取0.8～1.0；为初始切线模量，可根据原位载荷板试验的-曲线反算求解。

考虑到土体参数的匹配性，当切线模量随应力水平变化时，土体泊松比也应随应力水平做适当调整，相应的表达式为

=+(-)

(4)

式中，为破坏时的泊松比，一般取0.49；为初始泊松比。

1.2 变模量本构参数确定

岩土体力学参数的准确度对地基沉降计算结果的误差影响较大，因此地基沉降计算时应首先保证参数获取的准确性。

现场压板载荷试验是最接近基础受力状态的试验，且多数压板试验的荷载-沉降曲线接近双曲线形式。考虑到以上两点，杨光华等给出了初始切线模量的反算方法。该方法假定压板试验的荷载-沉降曲线为双曲线，相应的方程为

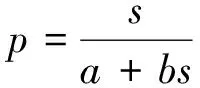
(5)

式中，为荷载；为沉降；，为参数，通过原位荷载-试验曲线拟合而得。

若将曲线转换为沉降-荷载曲线，则可表达为

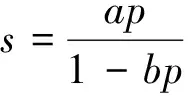
(6)

则极限状态下有

(7)

式中，为对应的地基极限承载力；为压板宽度或直径；为形状系数。

基于上述分析，可根据现场压板试验的沉降-荷载曲线拟合，，进而依据式(7)反算土体的初始切线模量和地基极限承载力，而后再根据Prandtl地基承载力公式，反算土体强度参数。

由于未受取样扰动，该方法确定的变形参数的准确度较高。

1.3 变模量本构合理性验证

为验证变模量本构在计算地基沉降方面的可靠性，基于C++将变模量本构嵌入到FLAC3D 5.0中，并通过有实测沉降值的压板试验算例，分析了变模量本构计算沉降的准确度。

压板试验算例介绍如下：压板载荷试验尺寸为0.8 m，试验影响范围纵横向均取12 m，影响深度取8 m，如图1所示。基于试验结果反算，黏土层初始切线模量取74 MPa，泊松比为0.3，黏聚力为42 kPa，内摩擦角为25°。

为凸显变模量本构模型在计算地基沉降方面的优越性，此处分别采用变模量本构和Mohr-Coulomb本构求解各分级荷载下压板的沉降量，并将之与实测结果对比，结果如图2所示。

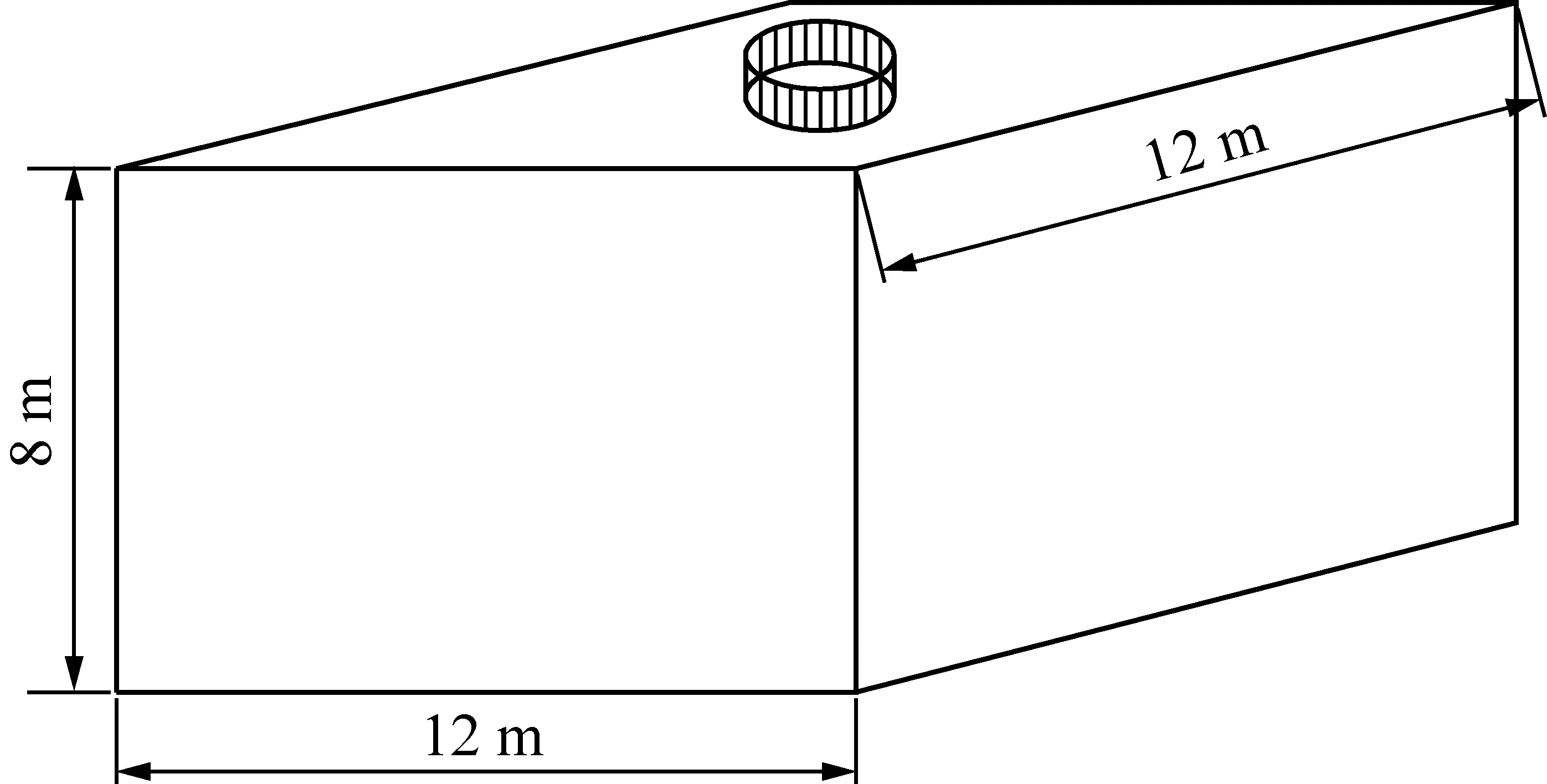
图1 压板载荷试验模型示意Fig.1 Diagram of load plate test

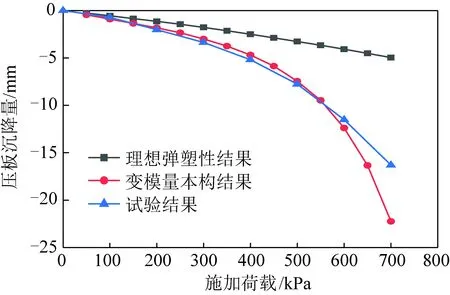
图2 不同方法所得压板试验荷载-沉降曲线Fig.2 Load-settlement curves for different methods

从图2可以看出：随着加载量的增长，基底沉降量呈非线性递增。基于Mohr-Coulomb本构所得沉降基本随荷载呈线性递增关系，而基于变模量本构的荷载-沉降曲线呈非线性特征，与实测荷载-沉降曲线的变化趋势吻合。随着荷载量的增长，基于Mohr-Coulomb本构所得沉降与实测沉降的差值越来越大，而各级荷载下，基于变模量本构的沉降量与实测沉降则较为接近。相较于弹性本构和Mohr-Colomb本构，变模量本构能描述岩土体在荷载作用下的非线性变形特征。

2 复杂地基三维沉降及应力特征

2.1 依托工程概述

荔湾商业大厦位于广州市环市西路，包含地上12层和地下2.5层，属框剪结构。基础形状不规则，最大横向宽度为61.5 m，最大纵向宽度为58 m，基础形状和尺寸如图3所示。沿基础纵向和横向进行了详细的地质勘探(4横3纵)，根据地质钻孔资料，底板下各岩土层依次为人工填土层、冲积层和残积层。其中人工填土层主要成分为粉质黏土，层厚0.8～3.0 m；冲积层以细沙为主，层厚1.1～2.3 m；残积层主要由风沙岩风化残积而成，可细分为粉质黏土、粉土、强风化带、中风化带和微风化带，各层厚度差异性较大，各地质剖面土层分布如图4所示。

整体上，基础尺寸较大，底板以下地质条件复杂，粉质黏土层厚度不均，中风化层埋藏深。在大面积荷载作用下，地基容易产生较大沉降和沉降差，可能会影响上部结构的应力状态。

2.2 计算模型及参数取值

为了较准确的分析底板下各位置处的沉降值，分析沉降差是否满足设计要求，综合考虑了纵横2方向7个剖面的地质情况，建立了荔湾大厦地基真三维数值模型，如图5所示。总体上，基础左下角黏土层较薄，右上角较厚。模型中包含291 438个节点，308 241个单元。采用变模量本构模型分析荷载作用下基底应力和沉降。依据荔湾大厦的层高和工程经验将基底工程荷载简化为210 kPa的均布力。

图3 基础形状及尺寸Fig.3 Shape and dimension of foundation

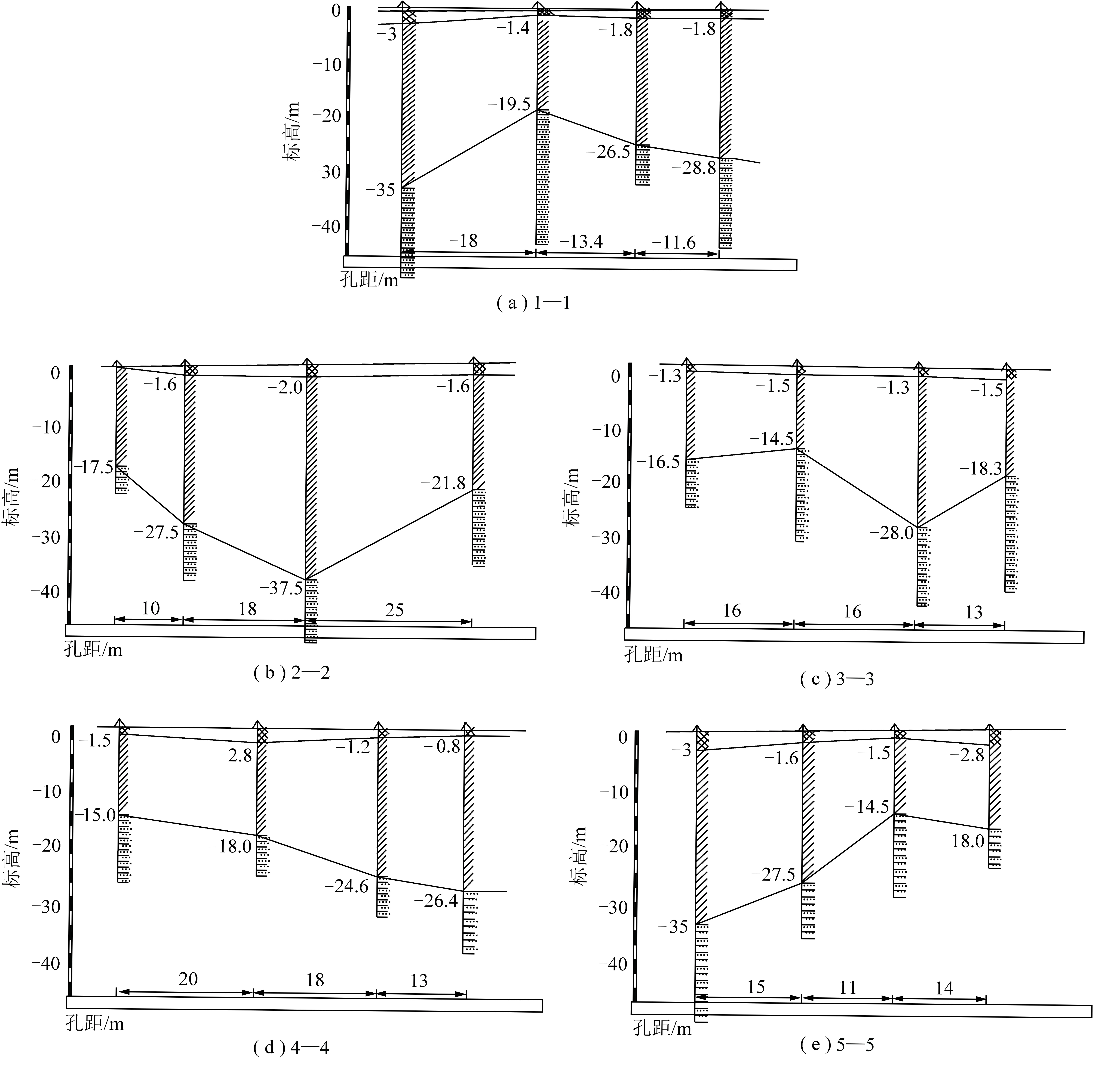
图4 各剖面地质情况Fig.4 Geological condition for different profiles

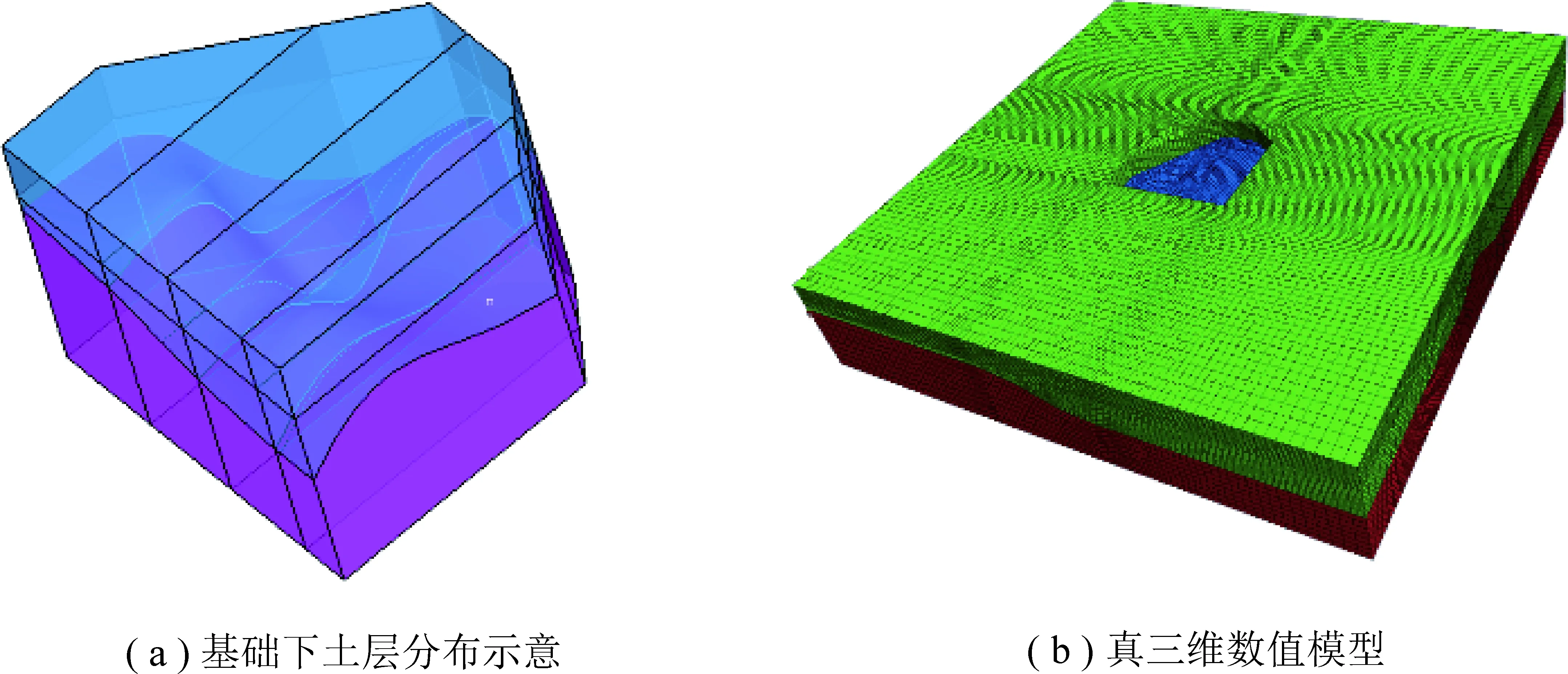
图5 荔湾大厦真三维数值模型Fig.5 3-D numerical model for Liwan building

基底土层变形和强度参数依据现场压板载荷试验数据推演得到。为较准确的获取地基承载力及变形参数，开展了3个压板试验，相应的加载及变形结果见表1。

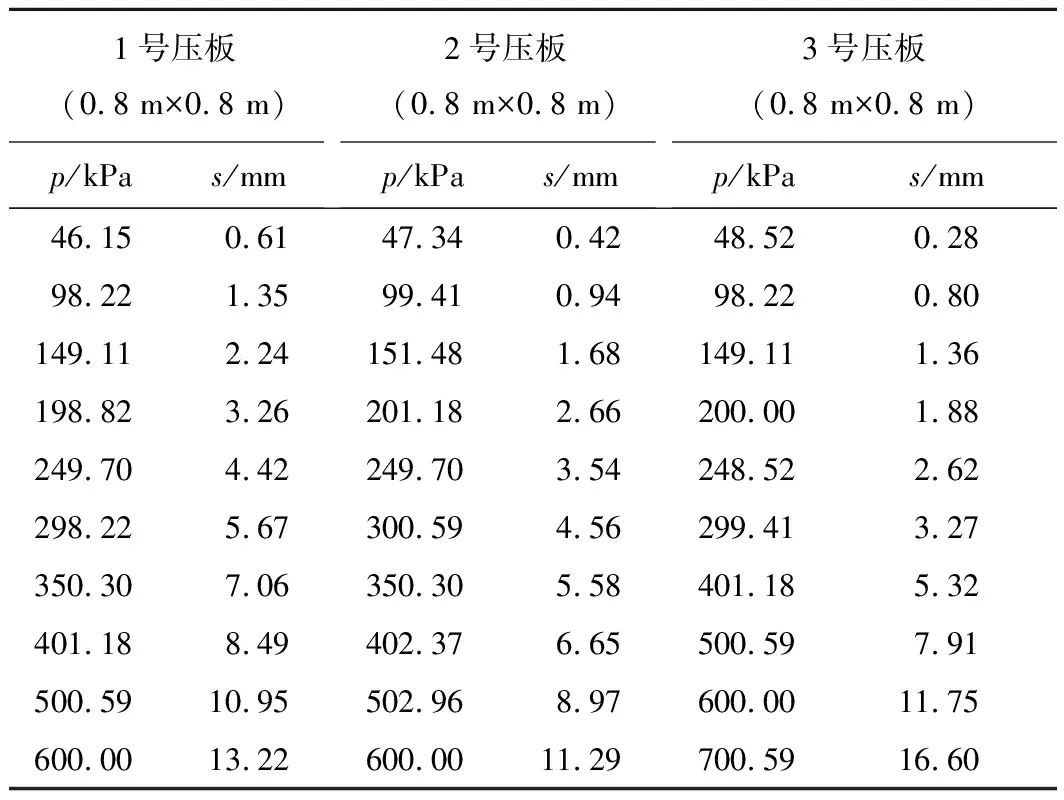
表1 荔湾大厦地基压板试验加载及变形情况

基于上述数据，依据2.2节的方法反算得到底板下粉质黏土层的初始切线模量和地基的极限承载力，并结合Prandtl极限承载力公式推演粉质黏土层的黏聚力和内摩擦角，而中风化层则依据经验对其变形和强度参数进行取值，各土层参数取值见表2。

表2 各土层力学参数统计Table 2 Mechanical parameters of soils

2.3 沉降及应力分布特征分析

基于变模量本构计算的荔湾大厦基底沉降等值线图如图6所示，工程实测沉降标记于图6的相应位置。基底沉降量总体上呈左下角小右上角大的趋势，沉降量介于40～54 mm，而实测沉降量介于38～43 mm。沉降量分布与黏土层厚度分布有关，黏土层厚度大处沉降量相应较大。为进一步分析计算沉降和实测沉降之间的差异，基于测点处实测值和计算值间的沉降差做了插值处理，并绘制成沉降差等值线图，如图7所示。

图6 基于变模量本构的基底沉降等值线Fig.6 Contour map of base settlement based onvariable modulus constitutive model

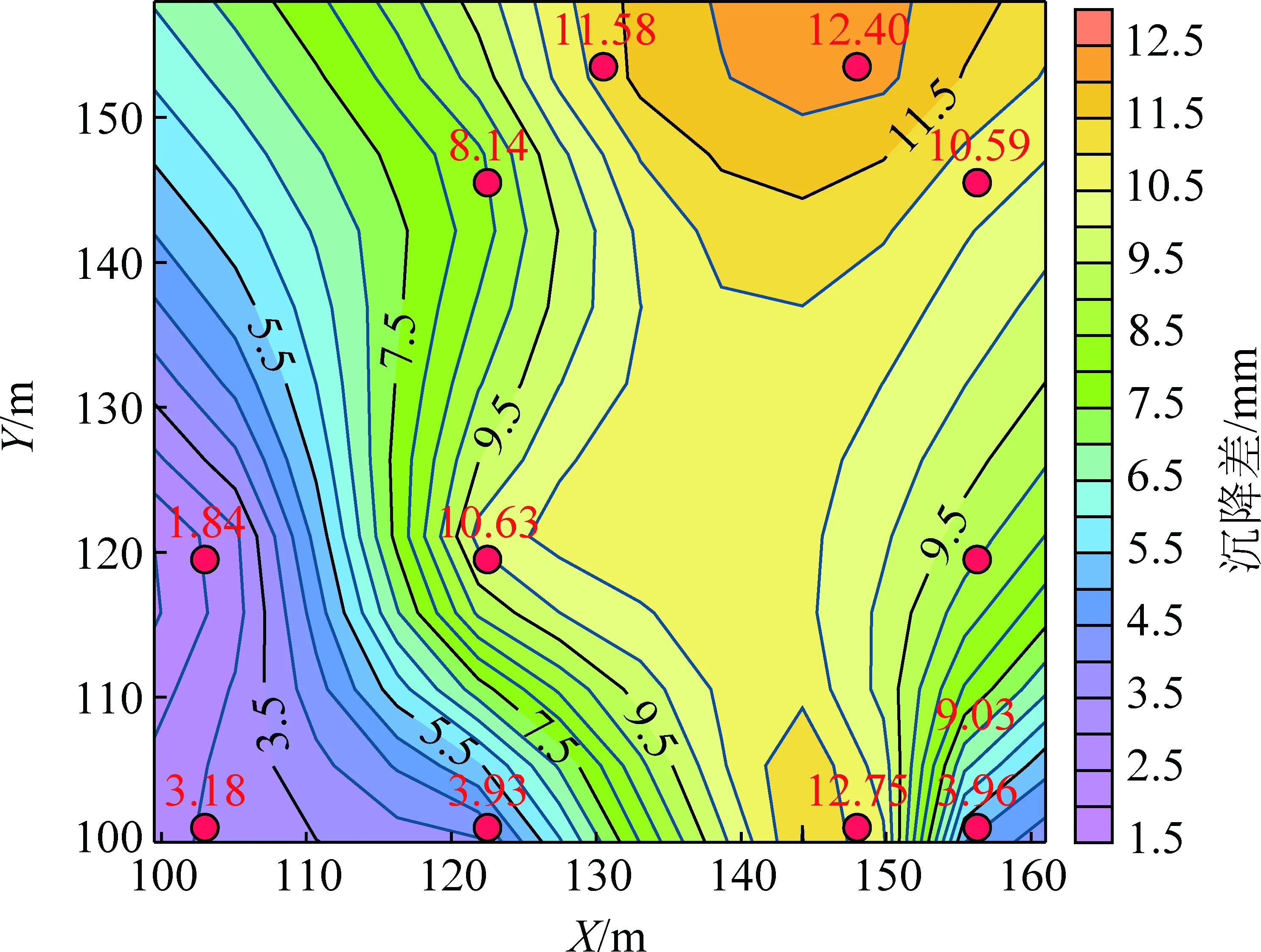
图7 计算沉降与实测沉降差等值线Fig.7 Contour of the difference between thecalculated settlement and the measured settlement

从图7可以看出，实测沉降与计算沉降差也呈现出左下角小右上角略大的特点，最小沉降差仅1.84 mm，最大沉降差达12.75 mm，计算沉降略大于实测值。

总体上计算沉降与实测沉降结果吻合度较高，说明变模量本构用于三维复杂地基沉降计算较为精准。

荔湾大厦基底应力分布如图8所示。总体上，荔湾大厦基底应力呈下侧大上部小的特征，尤其左下角应力集中程度较高。造成这种分布特征的原因是基底沉降的不均匀性。黏土层厚度小处沉降量较小，基础梁板与土层充分接触挤压而造成应力集中；而黏土层大处沉降量大，基础梁板与土体脱空应力得到释放。

为了更直观的分析地层对沉降和应力分布规律的影响，现将各地质剖面的沉降和应力沿地层分布的特征曲线如图9所示。

1—1剖面左右两侧黏土层厚度较大，中间黏土层厚度较小，对应的基底沉降相对均匀，右侧沉降量略大，沉降量约为50 mm；对应的基底应力则表现出两侧应力低中间应力大的特点，基底应力分布特征曲线呈现出与地层分布相符合的特征。

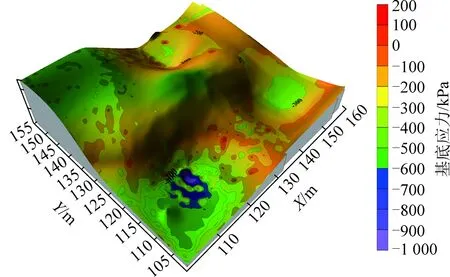
图8 基于变模量本构的基底应力等值线Fig.8 Contour of base stress based on variablemodulus constitutive model

2—2剖面左右两侧黏土层厚度相对较小，中间黏土层厚度较大，最大厚度距左边界25 m左右。受黏土层空间分布约束，右侧黏土层厚度小处反而较左侧沉降略大，左侧最小沉降约45 mm，右侧最大沉降约50 mm，由此体现出对于复杂地质条件的地基沉降分析，建立三维地质力学模型的必要性；应力呈现两端大中间小的分布特征，黏土层厚度较大处应力较低。

3—3剖面两侧黏土层厚度较小，中间黏土层较大，且右侧黏土层厚度略大于左侧；4—4剖面左侧黏土层厚度小，右侧黏土层厚度大。综合分析3—3剖面和4—4剖面的基底沉降和应力分布特征曲线，可以看出：地层分布不均时，基底沉降不对称，且基底应力呈现出与地层分布相适应的特征，黏土层厚度大处因变形较大应力得到释放，因而应力较低，而黏土层厚度小处应力较大。

5—5～7—7剖面为沿基础纵向平行分布的3个剖面。综合分析基底沉降、基底应力及地层分布特征，5—5～7—7剖面基底沉降和应力分布同样符合以下特征：① 地层分布不均时基底沉降不均匀，黏土层厚度大处沉降量较大；② 基底应力分布与地层分布相符合，黏土层厚度大处基底应力较小，黏土层厚度小处基底应力较高，且在地层厚度变化大处，应力集中明显。

总体上，基于变模量本构计算的荔湾大厦基底沉降与实测结果符合性较高。在地层分布不均的情况下，即便基础刚度较大，基底沉降分布也很难均匀，但刚度较大时，沉降差相对较小，应力分布则表现出与地层分布相符合的特征，即：黏土层厚度大处应力较低，黏土层厚度小处应力较大，且地层变化较大处应力存在突变特征。

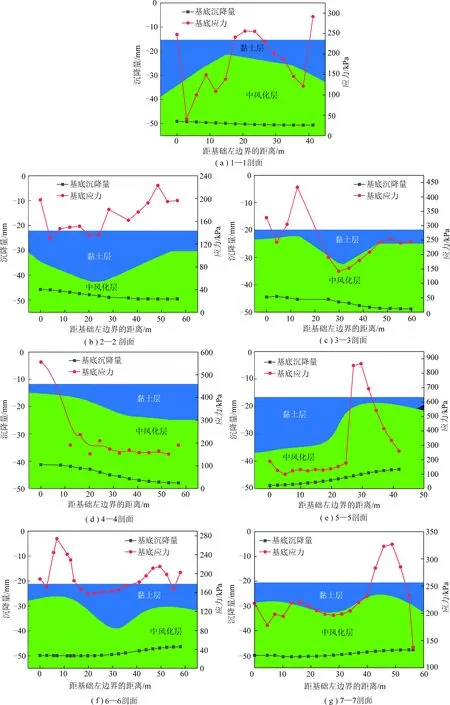
图9 7个剖面沉降、应力随地形分布特征曲线Fig.9 Characteristic curves of settlement and stress distribution over terrain for seven profile

3 沉降及应力特征影响因素分析

3.1 基础形状影响

为分析基础形状对地基沉降和应力分布特征的影响，特选取了矩形基础和荔湾大厦不规则基础作为对比，其中矩形基础长度与荔湾大厦不规则基础横向最大宽度一致，宽度则与荔湾大厦纵向最大宽度一致。为避免地层分布对计算结果的影响，此处选择等厚地层作为地质条件，基底以下黏土层深度为15 m，岩层深度为23 m。岩土体力学参数见表2，采用的本构模型仍为变模量本构，所建模型如图10所示。计算时假定基础为刚性基础。

图10 2种形状基础对应的模型Fig.10 Calculation model for rectangle and irregularshape foundation

通过图6，8分析基础形状的影响。相同附加荷载下矩形基础和荔湾大厦不规则基础对应的沉降和应力分布结果如图11，12所示。

从图11，12可以看出：基础形状不同时，基底沉降量及分布特征基本一致，但基底应力具有明显异同点：相同之处在于基底应力值相近，且均存在角点应力集中现象；不同之处在于，荔湾大厦不规则基础存在显著的边缘化集中现象，而矩形基础则不存在。

3.2 基础刚度影响

基础刚度对基底沉降和应力分布影响较大，为具体分析基础刚度的影响，以大面积荷载450 kPa为例分析了无刚度基础、混凝土梁板基础、钢梁板基础和10倍钢梁板基础4种类型基础刚度条件下基底的应力和沉降分布特征。为避免地层对规律的影响，采用均质等厚度粘性土作为地层条件。采用理想弹性本构和变模量本构进行同工况下的对比分析。

图11 不同形状基础基底沉降等值线Fig.11 Basement settlement contour for different shape foundations

不同基础刚度下基底沉降对比结果如图13所示，基底应力结果如图14所示。从图13，14可以看出：① 基础刚度对基底沉降分布有影响，采用柔性基础或混凝土梁板基础时，基底沉降沿基坑宽度呈现较大挠曲变形，随着刚度增大，挠曲程度骤减，基底沉降趋向于均匀化；同一工况下，变模量本构因能模拟土体的非线性沉降，因而所得沉降值比弹性结果大，且沉降分布更均匀；② 刚度越大，采用弹性本构模型所得基底应力端部集中程度更大，而变模量本构模型因能有效模拟土体屈服后的应力释放问题，基底端部应力不存在显著的集中问题，所得基底应力分布更符合工程实际。

因为底板方向的应力在一定程度上表征基础底板的弯矩特征，提取了基础为钢板情况下采用变模量本构和弹性本构所得基础底板方向的应力分布情况，如图15所示。可见，在刚度较大情况下，采用弹性本构模型也会过高估计基础底板的弯矩。

图12 不同形状基础基底应力等值线Fig.12 Basement stress contour for different shape foundations

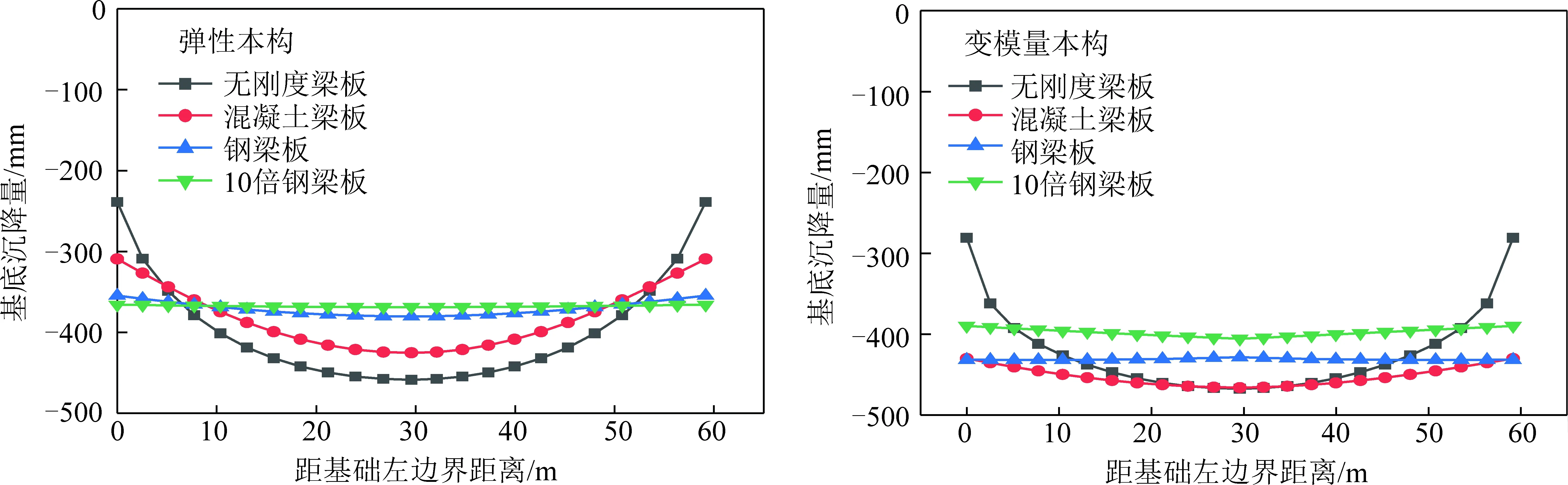
图13 基础刚度对沉降的影响Fig.13 Influence of foundation stiffness on settlement

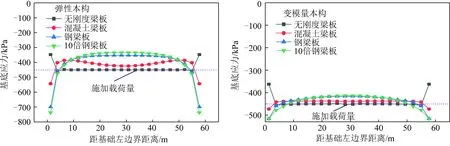
图14 基础刚度对基底应力的影响Fig.14 Influence of foundation stiffness on stress

由图14，15可知，在底板刚度较大情况下，弹性本构模型所得局部应力和底板弯矩过大，容易造成设计可行性的误判，而变模量本构模型因考虑了模量随应力水平的调整，所得结果更符合结构的真实受力状况。因此，在刚度较大情况下推荐采用变模量本构模型分析结构和基础的受力特征。

3.3 荷载大小影响

为分析荷载大小对基底沉降和应力的影响，以混凝土梁板基础为例，分别分析50 kPa小荷载、200 kPa中等荷载和450 kPa大荷载3个等级荷载作用下基底沉降和应力分布特征，并将荷载大小对基底沉降的影响结果如图16所示，对基底应力的影响结果如图17所示。

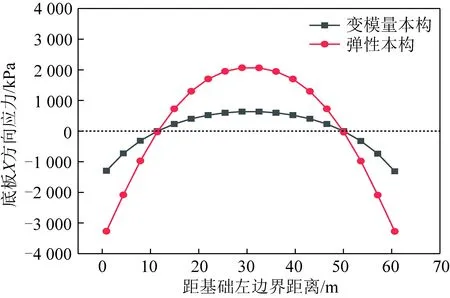
图15 不同计算方法对应的底板X方向应力Fig.15 X-direction stress of base plate fordifferent calculation methods

图16 荷载大小对沉降的影响Fig.16 Influence of load on base settlement

从图16可以看出：① 荷载大小影响基底沉降沿基础宽度的挠曲程度，荷载越大，挠曲程度越高；② 采用变模量本构计算时，因有效模拟了土体屈服后的应力释放问题，因此相同荷载下，变模量本构所得沉降更均匀。

图17的结果表明：① 荷载大小影响基底应力的分布形态，随着荷载的增大，端部应力集中程度增长，尤其是弹性本构对应结果更显著；② 当荷载为50 kPa或200 kPa时，采用弹性本构和变模量本构所得基底应力基本一致，当荷载达450 kPa时，弹性本构对应端部应力集中程度十分显著，而变模量本构因有效模拟了端部应力的释放问题所得基底应力相对均匀。

图17 荷载大小对基底应力的影响Fig.17 Influence of load on base stress

因此，对于大面积大荷载工程，为能较准确的评估基底沉降和应力是否满足工程需求，应采用变模量本构进行分析，以免造成对地基承载可行性的误判。

3.4 地层分布特征影响

基于前述荔湾大厦真三维模型结果可以大致得出地层分布对基底沉降和应力分布特征有影响，但具体影响还需进一步对比分析。为此以刚性基础和210 kPa的中等荷载为例分析了均匀等厚地层(图18(a))、不等厚对称地层(图18(b))和不等厚不对称地层(图18(c))3种地质条件下基底沉降和应力分布特征，并将不同地质条件下基底沉降和应力分布等值线整理于如图19所示。

图18 不同类别地层示意Fig.18 Diagram for different geological conditions

图19 不同类别地层沉降、应力分布等值线Fig.19 Settlement and stress distribution for different geological conditions

从图19可以看出：对于均匀等厚地层，基底沉降和应力分布相对均匀，基底沉降沿基础宽度存在轻微挠曲；对于不等厚均匀地层，因基础两侧黏土层厚度较小，而中间黏土层厚度较大，因而基底沉降存在两侧小而中间大、基底应力存在两侧应力集中而中间应力较低的现象，左右两侧沉降和应力值虽不完全一致，但相差不大；对于不等厚不均匀地层，基底沉降和应力等值线图呈现明显的不对称现象，左侧沉降小于右侧沉降、左侧应力明显高于右侧应力，在左侧应力集中现象突出。

为进一步分析不同类别地层条件下基底沉降和应力沿基础宽度分布特征，采用弹性本构和变模量本构2种方法绘制了不同类别地层沉降和应力分布曲线，如图20，21所示。

图20 不同类别地层沉降分布规律Fig.20 Settlement distribution for different geological conditions

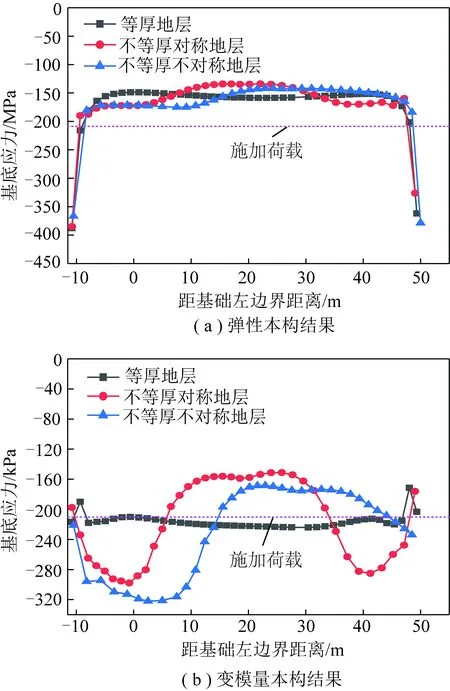
图21 不同类别地层应力分布规律Fig.21 Stress distribution for different geological conditions

同一地层条件下，采用弹性本构计算所得基底沉降明显小于变模量本构结果，对于等厚地层和不等厚对称地层，变模量本构所得沉降分布更均匀；采用弹性本构计算不同类别地层条件时均存在明显的端部应力集中现象，尤其对于不等厚不对称地层，端部应力甚至超过2倍的加载量。而采用变模量本构计算时，因能充分考虑屈服后应力释放，因而不存在显著的端部应力集中现象。当地层等厚时，基底沉降相对均匀，而当地层不等厚对称分布时，基底应力分布不均匀但对称；但当地层不等厚也不均匀分布时，即使两侧黏土层厚度相差不大，仍会产生明显的不均匀沉降和黏土层厚度较小处的显著的应力集中现象，而弹性本构无法模拟这种显著的应力差。弹性本构所反映的端部应力集中及无法刻画不等厚不均匀地层条件下的显著应力差问题可能导致2方面的问题：① 端部应力集中容易造成地基承载可行性的误判；② 容易忽视基础显著应力差对上部结构的影响。因此，应特别关注不等厚不对称地层条件下基底沉降和应力分布特征，采用恰当的计算方法加以分析，确保工程评估的准确性。