基于用电信息大数据的时间序列分析研究
2022-06-02王登峰窦圣霞汪海燕严绍奎
王登峰 ,窦圣霞 ,汪海燕 ,周 睿 ,严绍奎
(1.国网宁夏电力有限公司营销服务中心(国网宁夏电力有限公司计量中心),宁夏 银川 750011;2.国网(宁夏)综合能源服务有限公司,宁夏 银川 750011)
用电信息采集系统的核心设备是智能电表,目前正在国内外许多地区迅速取代传统电表。基于智能电表和电力大数据的智能电网一方面能够节省能源浪费、降低用电成本、提高电网运行可靠性;另一方面可确保电力生产和消费的有效连接和利用,实现电网的自动和实时管理,更好地测量能耗、优化可靠性水平并改善现有服务,从而节省能源并降低能耗费用[1-5]。
智能电网功能的实施基于在电网用电户安装的智能电表和各种传感器,导致要处理的数据量大大增加。例如智能电表以每15 min 发送一次用户消耗的能源的读数,每个电表每天可产生大量读数,而不是传统电表中每月一次读数。因此除了能源管理之外,智能电网还需要出色的数据管理来应对高速处理、存储和用电数据高级分析的要求。实际上由于智能电网数据的性质、分布和某些需求的实时约束,通常需要复杂的数据处理方法。而大数据技术恰好适用于此类高效数据管理工作,以帮助电网公司更好地了解客户的行为,实现节约用电和合理安排用电需求、跟踪停机时间和监测电源故障等。因此电网单位的主要目标是能够管理大量数据并通过数据分析将收集的数据转换为有效的知识,最后转换为可实施的电力服务计划[6-10]。
因此本文采集了100 个匿名商业建筑的5 min智能电表数据集,进行了全面的分析,探索用电的时间序列以及用电行为的预测方法,通过对比不同预测模型效果验证了本文构建的预测模型的合理性。研究结果可为基于电力大数据的用户用电行为预测提供参考。
1 基于智能电表大数据的计量体系结构
1.1 用电信息采集系统的组成
用电信息采集系统是由智能电表、通信网络和数据管理系统组成的集成系统,可实现公用事业和客户之间的双向通信[11]。该系统提供了许多以前无法实现或必须手动执行的重要功能,例如自动和远程测量用电量情况、连接和断开服务、篡改和盗窃用电监测、故障和断电识别以及电压监测等[12]。
用电信息采集系统的体系构架通常包括以下几个关键组件:
(1)智能电表:用电信息采集系统的核心元素是智能电表,该电表安装在客户的房屋内,并提供多种功能:包括以5 min、15 min、30 min 或60 min 的间隔测量客户的用电量;测量电压电平;监视电力服务的通断状态。智能电表将这些读数传达给电网相关单位,以进行处理、分析、回馈给客户进行计费等。
(2)通信网络:可将大量由智能电表采集的不同时间间隔的电力负载数据,从电表传输到电网公司的后台。
(3)电表数据管理系统(meter data management system,MDMS),用于存储和处理不同间隔时间的电力负荷数据,并将电表数据与多个关键信息和控制系统进行集成,这些系统包括有头端系统、计费系统、客户信息系统(customer information systems,CIS)、地理信息系统(geographic information systems,GIS)、停运管理系统(outage management systems,OMS)和配电管理系统(distribution management systems,DMS)。
推动用电信息采集系统投资的主要新功能是能够自动生成及时且准确的账单,而不受天气条件或物业使用限制的影响,传统上这会妨碍电表信息的收集。一旦正确配置,用电信息采集系统和计费系统将自动生成更一致、更准确的账单,并减少记录错误和客户投诉。由于可以以15 min 为增量指定数据间隔,因此公用事业公司可以根据客户偏好而不是根据公用事业公司设置的抄表时间表自定义计费周期。
1.2 智能电表电力数据集
本文采用一个2019 年采集的由100 个商业化行业场所的5 min 能源使用数据,数据文件的每一行包含以下值:时间戳、日期时间、电量读取值、估计指标,异常指标等。其中“estimated indicator”是一个布尔值,指示是否估计读数,如果读数错误则“异常指示器”为空;能源数据的计量单位为kWh。如表1 所示是数据集的示例数据内容,表2 是数据标号及其所代表的用电户类型:

表1 数据ID=213(学校用电)的示例数据

表2 数据站点标号及用电户类型
2 基于电力大数据的时间序列模型
2.1 时间序列模型
根据先前的数据,可以通过时间序列得到未来物理量的变化情况,使得时间序列可用于预测经济、天气、能源消耗等方面,时间序列基本上是在基于时间(年,日,小时和分钟)的数据上进行探索分析,以对未来的能源消耗进行量化预测。本文构建了用电量预测模型对用户电力消费进行预测,模型主要组成部分及内容如下所示:
(1)ARIMA 模型:基于时间序列的预测中,最常用的方法之一就是ARIMA 模型,其基本原理是自动回归综合移动平均值,ARIMA 可以将数据按照时间序列进行拟合,以更好地预测序列中的未来点。模型中通过三个不同的整数(p,d,q)实现ARIMA 模型的参数化。因此ARIMA 模型用ARIMA(p,d,q)表示,这三个参数共同反映了数据集中的周期性、趋势性和噪声[13]。
(a)参数p是模型的自回归部分,可以将过去值的影响纳入模型,这一过程可以类比为:如果过去三天一直温暖,明天可能会温暖。
(b)d是模型的集成部分,模型中通过差分(即从当前值中减去的过去时间点的数量)应用于时间序列,从直觉上讲,这一过程可以类比为:如果最近三天的温差很小,则明天的温度可能相同。
(c)q是模型的移动平均线部分,通过该参数可以将模型的误差设置为过去在先前时间点观察到的误差值的线性组合。
周期性ARIMA 参数较多,调整过程复杂,因此需要为周期性ARIMA 时间序列模型构建自动识别最佳参数集。
(2)指数平滑:通过指数平滑可以平滑时间序列,随着观测值的增长,指数平滑法分配的权重呈指数下降趋势[14],指数平滑法是一种通过更好的预测从数据中去除“噪声”(随机效应)来“平滑”数据的方法。该方法的输入是n项时间序列值和平滑因子α,该算法的输出是时间n+T的预测值,指数平滑预测算法主要有以下几个步骤:
第1 步 输入具有n项时间序列的数据和平滑因子α的顺序原始数据集
第2 步 计算单指数平滑
第3 步 计算双指数平滑
第4 步 计算平滑系数an和bn
第5 步 计算预测值Yn+T。
(3)STL 分解:STL 分解是一种用于分解时间序列的方法,其基本原理是一种非线性关系的估计方法,首先读入数据,然后对数值矩阵进行反变换,就可以获得分解矩阵。将0<λ<1 的数据通过Box-Cox 变换获得加法和乘法之间的分解值,其中λ=0 的值对应于乘法分解,λ=1 的值对应于加法分解。
2.2 数据分析算法设计及数据可视化
本文基于随机森林算法对时间序列数据进行分析与预测,从原始数据集中随机抽取训练样本,训练得到单个学习机,这些学习机就是算法中的回归树,重复这一过程生成多个回归树组成随机森林,并由所有树的预测值的平均值决定最终预测结果。本文按照如下步骤构建随机森林算法:
(1)随机有放回地从N个原始训练样本中选择n(n<N)个样本生成m个训练子集。
(2)使用训练子集训练回归树,在节点上所有的样本特征中随机选择一部分样本特征,依据最小均方差进行回归树的左右子树划分,递归建树直到满足终止条件。
(3)重复以上步骤,将多棵回归树组成随机森林。
(4)将测试样本输入随机森林回归模型,取所有树预测值的平均值作为最终预测结果,并与实际值对比,评价模型的拟合效果。模型步骤如图2 所示:

图2 随机森林算法设计示意图
利用本文构建的时间序列预测模型进行智能电表大数据分析,采用apache spark 框架以及”R”语言实现数据可视化。各个行业频率表如表3 所示:
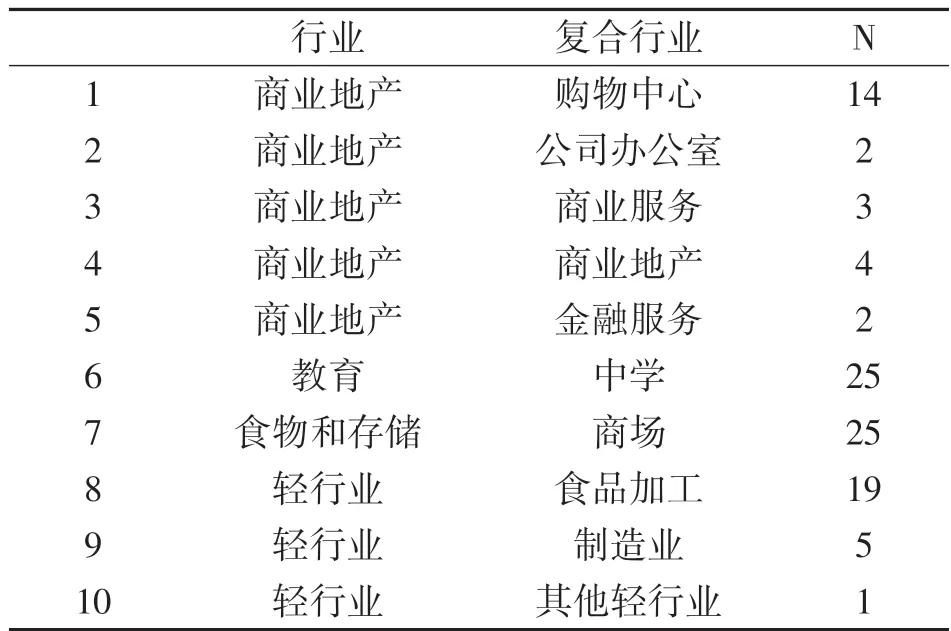
表3 行业类别与子行业频率表
如图3 所示是所有用电户的建筑面积SQ-M 数据直方图,由图可见本文数据集的建筑物,大部分建筑面积都在20 000 m2以下。
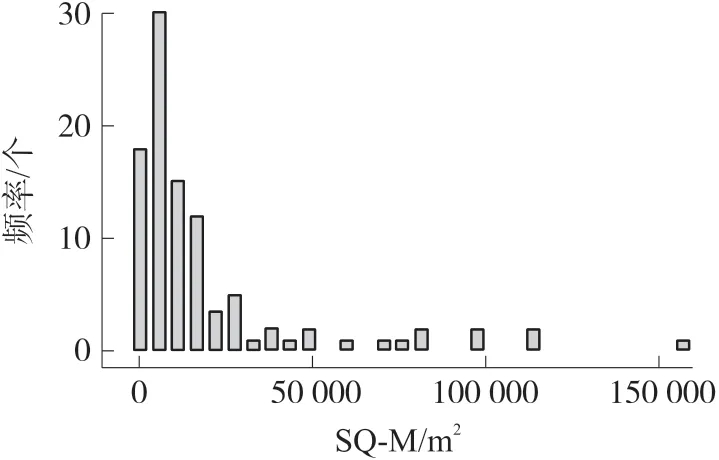
图3 用电户的建筑面积直方图
对4 个行业的建筑面积创建密度图,如图4 所示,由图可见食品销售与存储业的建筑物的面积相对较小,而商业地产建筑物的面积变化很大。
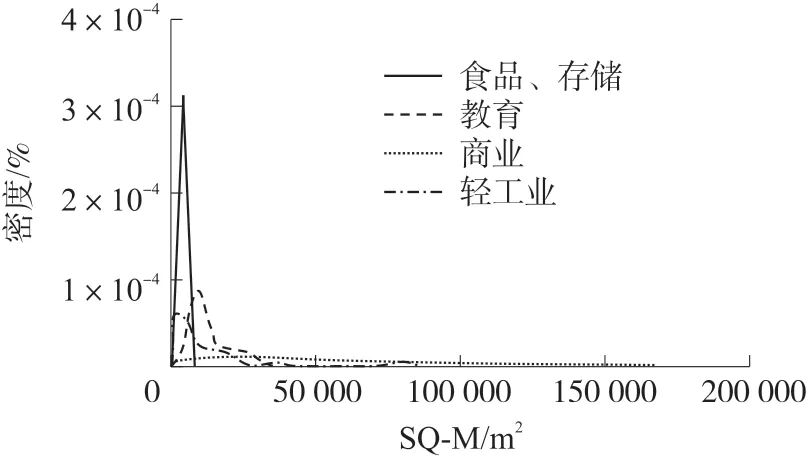
图4 4 个行业的建筑面积密度图
之后将建筑面积数据与实际用电量数据结合,就可以得到建筑面积与用电量的关系,如图5 所示是子行业的平均负荷条形图,由图可知,平均而言用电量最大的用户是制造业、购物中心和商业服务大楼;而用电量最低的用户是学校。
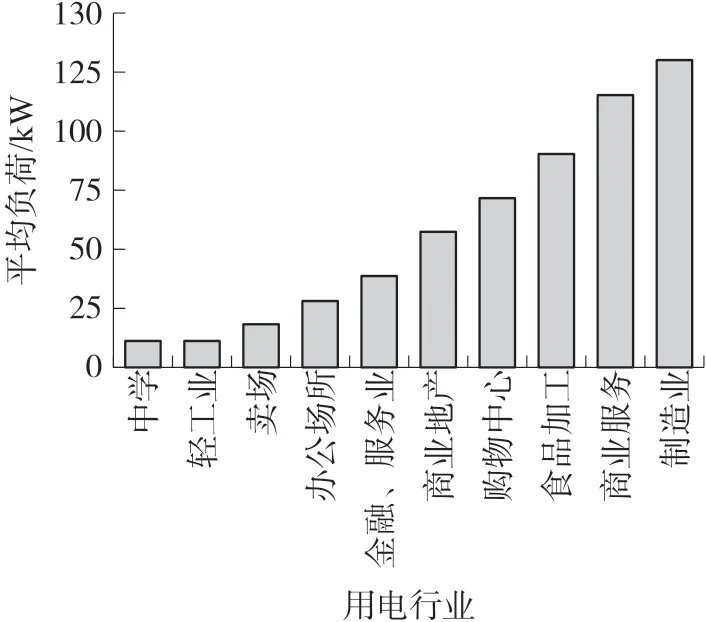
图5 子行业的平均用电负载条形图
如图6 所示是用电消耗量和SQ-M 之间的依赖关系,采用中位数负荷和简单的线性回归对该关系进行分析,图6 显示了回归线SQ-M 与中位数负载的关系。由图中可见负载的中位数与用电户的建筑面积之间存在明显的相关性。
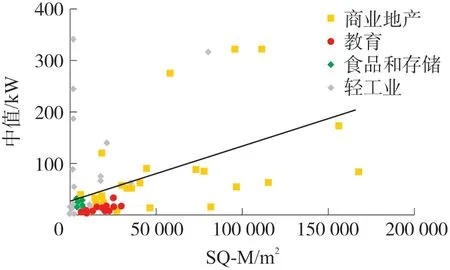
图6 回归线SQ-M 与中位负载
3 结果与讨论
如图7 所示是学校用电户的日用电、周用电和月用电消耗量,以及相应的时间序列数据,由图中可见用电量的多少与时间有显著的依赖关系,表明用电量随着时间的不同可能存在周期性的变化。
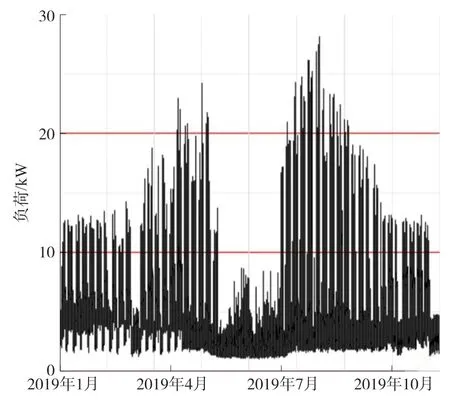
图7 一个ID 的每月消费(学校)
将时间序列汇总到较小的维度,从而将数据维度从每天288 个测量值减少到每天48 个,如图8 所示是4 个子行业组的典型用电数据。其中ID 213数据取自中学;ID 401 取自购物商场和市场;ID 832取自公司办公室;ID 9 取自工厂用电数据。

图8 4 个子行业组的代表
对于电网公司来说,创建消费者的每日用电信息资料或某个区域的每日用电信息非常有帮助,该资料有助于了解消费者的典型电力消费行为。为此本文采用MAD(中位数绝对偏差)创建了总用电的每日中位数,如图9 所示:
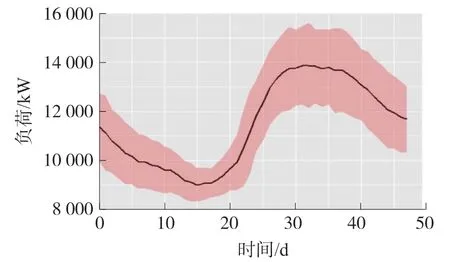
图9 MAD 每日总消费中位数
从图9 可以看出,最大的负载峰值出现的时间是在傍晚。同样使用周用电量模式来执行此操作,同样可根据MAD 得出每周总消费的中位数,如图10 所示:

图10 MAD 每周总消费中位数
由图10、图11 可以看出一周内用电户的电力消费行为具有5 种不同模式(以垂直线分隔):从星期一到星期五,电力消费量非常相似,但是星期一开始时的消费量较低,因此与其他消费量有所不同。周五的情况与此类似,但消费量比周四低一些。显然,周末与工作日完全不同,而星期六和星期日也不同。如果按照MAD(中位数绝对偏差)对子行业进行每周中位数计算,将会得到不同的用电模式,对于制造业得到的结果如图11 所示:
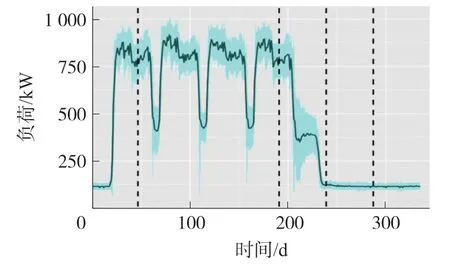
图11 每周制造业中位数
由图10~12 的分析可见,不同行业的电力消耗各自具有不同的特点,各个行业的电力消耗随着时间变化表现出不同的周围性规律,如此一来即可作为原始时间序列样本输入到模型中,从而为一周时间内的不同日期创建预测模型。使用相似日方法针对以每天为单位的用电数据建立预测模型。
首先定义基本的预测方法函数,这些函数用于产生预测结果。本文使用基于时间序列分解的STL+ARIMA 方法、STL+指数平滑方法以及传统时间序列方法进行预测。最后基于Loess 回归方法和STL分解对季节性时间序列进行分解,通过打包预测序列,可以将其组合以生成非常准确的预测结果。本文同时使用STL+ARIMA 方法和STL+指数平滑方法进行预测并对比其预测结果,如图12 所示:
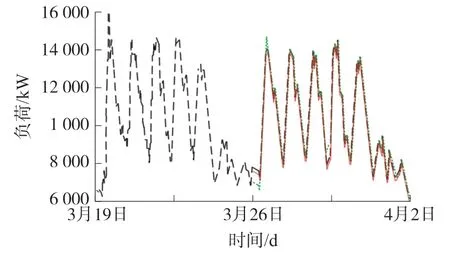
图12 两种模型的预测结果
其中黑色虚线是真实用电数据,原点数据是采用指数平滑的预测结果;实线是采用ARIMA 模型的预测结果。由图中可见ARIMA 模型对于电力消费行为预测更加准确。如图13 所示是未来一周的电力消费量预测图,表4 所示是各种预测模型的平均误差。
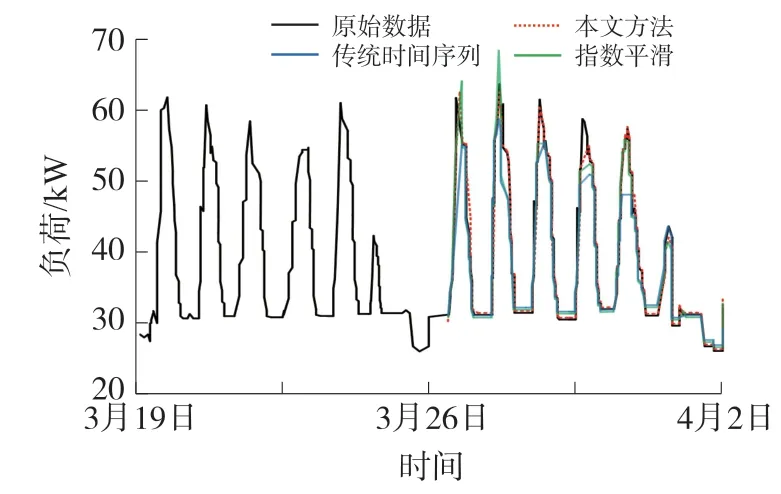
图13 未来一周的电力消费预测结果图

表4 预测模型误差统计表
由图14 和表4 可见采用本文预测模型得到的预测结果比指数平滑模型得到的预测结果更加准确。综上所述,本文提出的基于智能电表大数据的电力消费量预测模型,不仅能够根据用电的日、周、月数据进行对应时间周期的电力消费行为预测,而且预测精度比指数预测模型更加精确。
4 结论
智能电表数据分析是一个复杂的过程,涉及数据提取、预处理、分析和可视化。为此本文对100 个匿名商业建筑的5 min 智能电表数据集进行了全面分析,得到以下几个主要结论:
(1)电力消耗量与用电户的建筑面积具有明显相关性,表明智能电表的广泛应用,有助于电网单位增强客户用电服务、降低成本和提高能源效率。
(2)通过应用ARIMA、指数平滑等方法对不同行业的各个子行业层面进行的分析对比,表明本文构建的预测模型具有更高的预测精度。
